基于Fluent的电磁卸荷阀主阀流场数值仿真分析

秦海初，赵东升

（山西中煤华晋能源有限责任公司，山西 河津 043300）

1 电磁卸荷主阀二维仿真模型的建立

在建立二维仿真模型时应考虑所建模型的实际结构、模型参数必须与实际物理模型相一致；建立的模型不能过于复杂，也不能过于简化，过于复杂或者简化都会使得仿真计算结果不能够准确地反映研究对象的本质。

本文所要研究的电磁卸荷主阀的二维几何模型如图1 所示。将用AutoCAD绘制出的卸荷主阀的二维模型导入到Gambit中生成非结构化网格模型，如图2 所示。

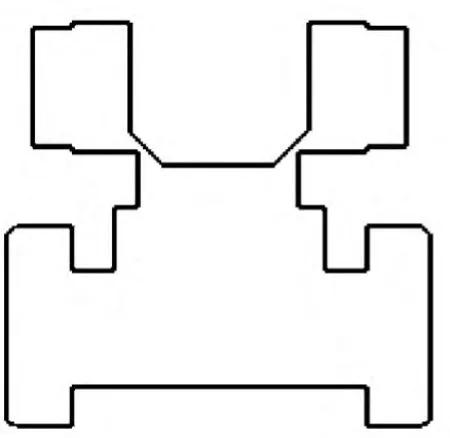
图1 电磁卸荷主阀几何模型

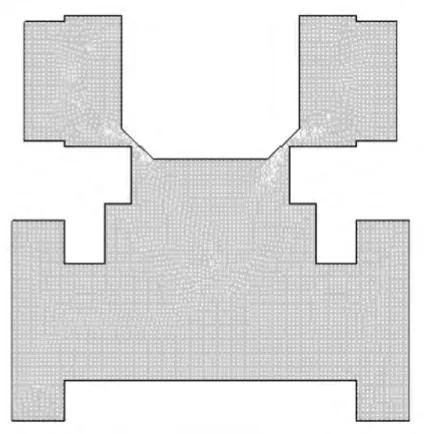
图2 电磁卸荷主阀的二维 网格模型

2 建立电磁卸荷主阀仿真模型的条件

电磁卸荷主阀仿真模型的建立是基于以下假设条件：①工作介质为不可压缩的液态水，为黏性牛顿流体；②不考虑工作介质的自身重量以及阀体流道内的能量交换；③将近壁面二维网格上的物理量按照标准壁面函数来计算；④利用有限元分析法建立仿真模型的离散数学方程，采用SIMPLEC算法来耦合压力速度，初始化流场从工作介质进入电磁卸荷主阀的入口计算。

3 仿真分析

3.1 主阀开口度不同

当工作介质进入电磁卸荷主阀入口的压力为31.5MPa、出口压力为0.1MPa时，利用建立的仿真模型分别对主阀开口度为1.5mm和3mm的主阀内流体进行仿真计算，得出了主阀开口度不同时阀内流体的压力、速度分布图，如图3 ～图6 所示。

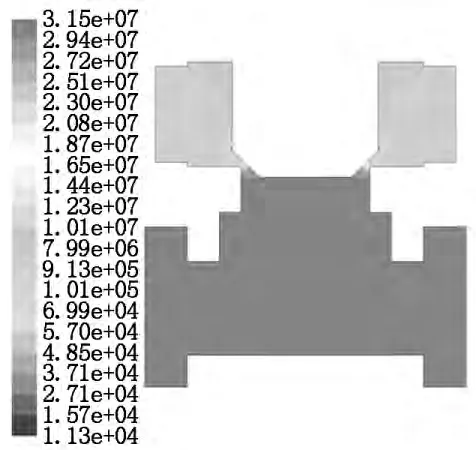
图3 主阀开口1.5mm时流体压力分布

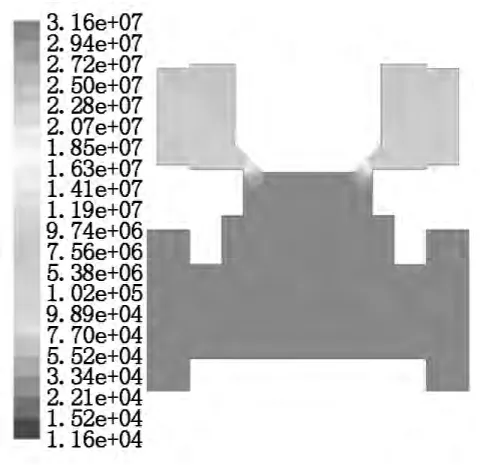
图4 主阀开口3.0mm时 流体压力分布

从图3 和图4 中可以看出：当主阀的开口度为1.5mm时，阀口拐角处压力为0.011 8MPa，当主阀开口度为3mm时，阀口拐角处压力为0.013 2MPa，即主阀阀口的压力随着主阀开口度的增大而加大；主阀内流体压力在阀口处变化比较剧烈，主阀开口度越大，流经主阀的工作介质的能量损失越少。

主阀阀口拐角处由于气泡聚集，容易产生气穴，阀芯和阀口处易遭到气蚀损坏。由于在阀腔内远离阀口处工作介质的射流扩散、流速较低、压强较高，从阀口至远离阀口的位置上，轴向压力分布逐渐减大，产生轴向稳态液动力。

从图5 和图6 中可以看出：当主阀开口分别为1.5mm和3mm时，阀口最大流速分别为为229.76 m／s和216.08m／s，工作介质在阀口处的流速随着主阀阀芯开口度的增大而减小。由于锥角本身具有一定的导流作用，因此工作介质在主阀阀口处的射流角基本上与锥角角度相同，不受阀口开口度的影响。

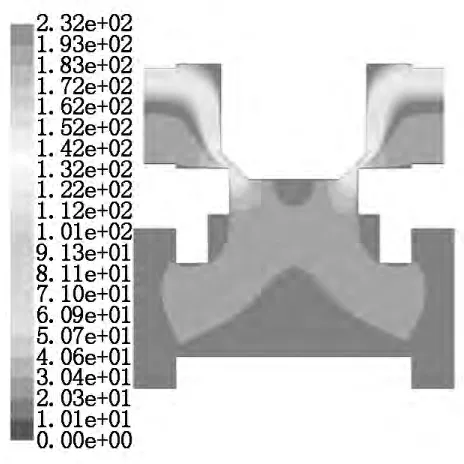
图5 主阀开口1.5mm时流体速度分布图

图6 主阀开口3.0 mm时 流体速度分布图

3.2 入口压力不同

主阀开口度一定，均为1.5mm，出口压力为0.1 MPa，其他边界条件不变的情况下，利用建立的仿真模型分别对入口压力分别为30MPa和33MPa时进行仿真计算。得出了入口压力不同时，阀内流体的压力、速度分布，如图7 ～图1 0所示。

图7 入口压力为30MPa时流体压力分布

图8 入口压力为33MPa时 流体压力分布

从图7 和图8 中可以看出：入口压力为30MPa和33MPa时，主阀阀口拐角处压力分别为0.025 MPa～0.053MPa和0.001 8MPa～0.012MPa。压力均小于液态水的饱和蒸汽气压，会有气穴现象产生。

从图9和图1 0中可以看出：在入口压力分别为30MPa和33MPa时，最大流速分别为217m／s和249m／s，阀口处的流速最大。入口的压力越大，主阀阀口处的流速越大。

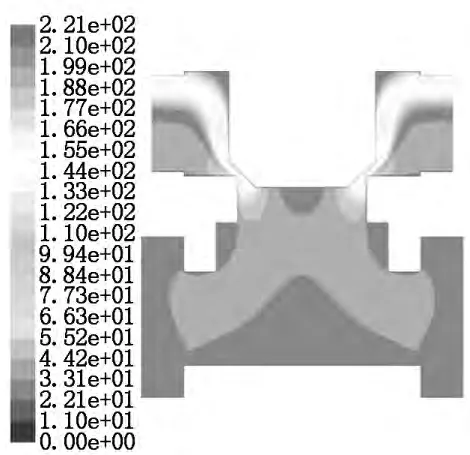
图9 入口压力为30MPa时流体流速分布

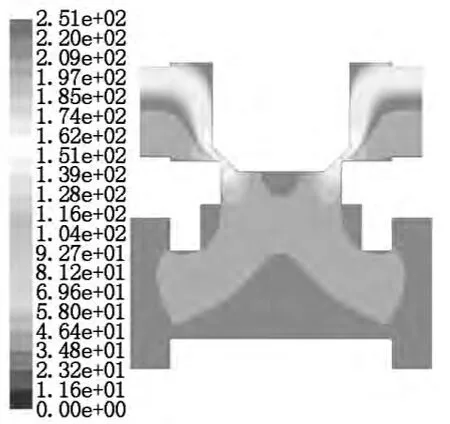
图1 0 入口压力为33MPa时 流体流速分布

4 主阀结构改进

基于以上仿真结果，对电磁卸荷阀主阀的结构进行了改造，在阀口处增加节流口，得到了新的流道几何模型，如图1 1所示。

改进前、后主阀流道内压力分布对比如图1 2所示。从图1 2中可以看出：在主阀开口度、入口压力、出口压力均一定的情况下，改造后主阀阀口的压差远远小于改进前。气穴现象仍然存在，低压范围明显缩小了，所以增加节流口能有效地减少气蚀损害，提高电磁阀的使用寿命。

图1 1 改造后主阀的几何模型

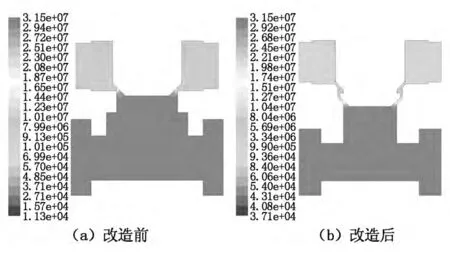
图1 2 改进前、后主阀流道内压力分布对比

改进前、后流道内流体速度对比如图1 3所示。可以看出，增加节流口后与改造前相比，阀口流体速度有了明显的降低，减少了工作介质对阀口产生的瞬间冲击，减轻了阀芯的振动。

5 结语

本文利用Fluent软件建立了乳化液泵站电磁卸荷阀主阀的二维网格仿真模型，得出了不同开口度、不同入口压力时，阀内流体压力、速度分布图。分析了主阀开口度、入口压力对流道内流体的压力、速度的影响。得出增加节流口，可减少工作介质对阀口产生的瞬间冲击，减轻阀芯的振动，减少气蚀损害，提高电磁阀的使用寿命。

图1 3 改进前、后流道内流体速度对比

［1］张宏，廉自生.基于CFD和两相流技术的高水基液压阀结构设计研究［J］.煤矿机电，2007（5）：1-4.

［2］王艳珍，于兰英.水压锥阀内流场的数值模拟［J］.兰州理工大学学报，2007，33（4）：54-58.

［3］付文智，李明哲.滑阀式换向阀三维流体速度场的数值模拟［J］.哈尔滨工业大学学报，2007，39（1）：150-153.