基于邻域极值数的协同粒子群优化算法

曾毅，朱旭生，廖国勇

（华东交通大学理学院，江西南昌330013）

基于邻域极值数的协同粒子群优化算法

曾毅，朱旭生，廖国勇

（华东交通大学理学院，江西南昌330013）

提出了一种基于邻域极值数的协同粒子群优化算法。该算法将种群分为若干个独立进化的子种群。根据邻域极值数确定各子种群的生存状态。根据子种群的生存状态对子种群实施相应的控制操作，提高子种群的搜索能力，实现子种群之间的信息共享，共同进化。测试结果表明基于邻域极值数的协同粒子群优化算法是一种高效稳健的全局优化算法。

粒子群优化算法；协同进化；邻域极值数

粒子群优化（particle swarm optimization，PSO）算法是由Kennedy和Eberhart等人于1995年提出的一种基于群体智能的演化计算技术［1］。算法基本思想源于对鸟群扑食行为的研究，是对简单社会系统的模拟。由于PSO算法具有很好的生物社会背景而易理解、结构简单、参数少而易实现，算法提出后受到了学者的重视和研究。目前，已经广泛应用于许多领域［2］。

粒子群优化算法通过种群粒子之间的合作与竞争实现对问题最优解的搜索，可用于解决大量非线性、不可微和多峰值等优化问题。但在求解高维复杂函数优化问题时，进化前期收敛速度快，进化后期极易陷入局部最优解，收敛速度和解的精度也不理想。针对这一问题，文献［3］提出基于高斯变异的粒子群算法，算法按预先设置的概率对粒子进行高斯变异操作，改善了种群的多样性，有利于变异粒子跳出局部极值点进行全局搜索，收敛速度和精度也有一定程度的提高。文献［4］分析了不同的种群拓扑结构对PSO算法效能的影响，提出了构造种群拓扑结构的基本原则。文献［5-6］提出多种群协同粒子群优化算法，测试结果表明能提高算法的收敛性。本文提出了一种基于邻域极值数的协同粒子群优化算法。测试结果表明基于邻域极值数的协同粒子群优化算法的有效性。

1 标准粒子群优化算法

本文讨论如下数值优化问题

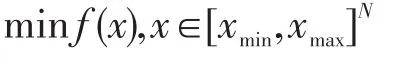
其中：N为搜索空间的维数。

标准粒子群优化算法将每个个体看成N维搜索空间中的一个没有质量和体积的粒子，并以一定的速度飞行。飞行速度由个体的飞行经验和群体的飞行经验进行动态调整。标准粒子群优化算法根据式（1）

（2）更新粒子速度和位置。

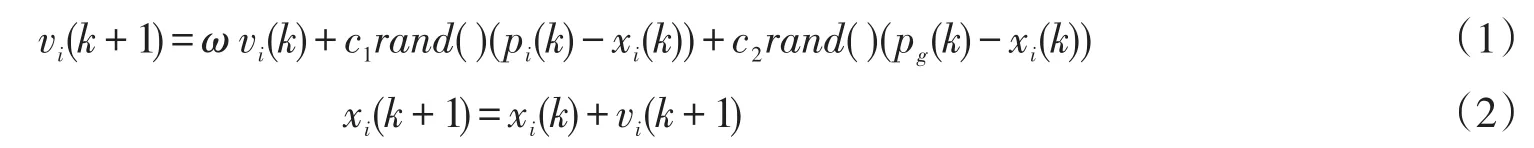
其中：vi(k)为粒子i在第k代的速度；xi(k)为粒子i在第k代的位置；ω为惯性权重；rand()为分布于[0,1]之间的随机数；c1为认知系数；c2为社会系数；pi(k)为粒子i个体历史最优位置，也称为个体极值；pg(k)为群体历史最优位置，也称为全局极值。为保证算法的稳定性，算法定义了一个最大速度上限vmax，用以限制粒子速度的大小，即

粒子在搜索空间内不断跟踪个体极值及全局极值进行搜索，直到达到规定的迭代次数或满足规定的误差标准为止。

2 种群的生存状态［7］

在一次优化搜索中，一个种群从初始化直至最终成熟的整个过程定义为该种群的生命周期。一般来说，在搜索初期，种群的分布最分散，多样性最好，搜索能力最强；在搜索中期，种群的多样性和搜索能力会逐渐降低，但依然会保持在相对较高水平；进入搜索后期，种群的多样性和搜索能力会降低至一个相对较低水平，变化速度趋缓。为了能够准确地引导种群的寻优过程，根据种群的搜索特征将种群的生存状态划分为成长初期、成长中期和成熟期3个时期。为此，给出邻域空间、邻域极值和邻域极值数的定义，并根据邻域极值数确定种群的生存状态。

定义1在第k代种群中，与粒子i欧氏距离最近的num个粒子的集合称为粒子i的邻域空间［8］。

定义2在第k代种群中，粒子i的邻域空间最优粒子的位置，称为粒子i的第k代的邻域极值。每个粒子都有邻域极值，且不同的粒子的邻域极值可能相同。

定义3在第k代种群中，若粒子j的位置xj(k)为种群中mj(k)个粒子的第k代邻域极值，称mj(k)为粒子j的邻域极值数。记

并称m(k)为第k代种群的邻域极值数。因为m(k)的大小反映了种群多样性和搜索能力，所以可利用m(k)的大小来确定种群的生存状态。

定义4若m(k)＜K1，K1的经验取值为，其中n为种群规模，则认为种群的生存状态为成长初期；若K1≤m(k)＜K2，K2的经验取值为，则认为种群的生存状态为成长中期；若m(k)≥K2，则认为种群的生存状态为成熟期。

3 控制操作

根据种群所处的生存状态，对种群实施相应的控制操作，更有利于调控种群的局部搜索和全局搜索的平衡，进而提升算法的性能。

1）当种群处于成长初期时，为了使种群有较好的多样性和搜索能力，此时应减少种群最优粒子的对种群粒子的影响，增加邻域空间最优粒子对种群粒子的影响，防止粒子迅速地向种群最优位置聚集，能有效地提高种群局部搜索能力，在一定程度上避免早熟现象的发生［9］。为此，本文根据式（5）（6）更新粒子速度和位置

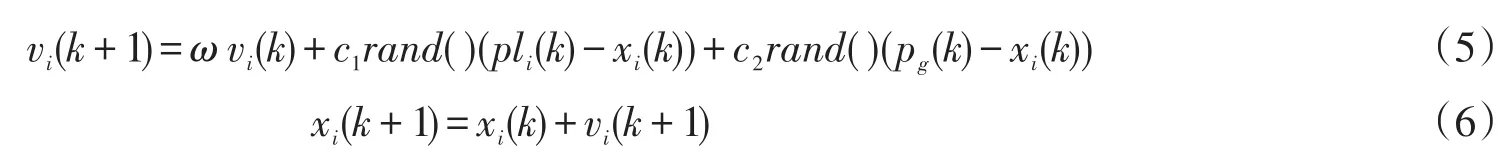
其中：pli(k)为粒子i的历史最优邻域极值，其余记号与式（1）（2）中的意义相同。

2）当种群处于成长中期时，此时种群所在的搜索区域还没有完全被开发。为进一步开发搜索区域，对邻域极值数大于K1，小于K2的粒子实施单变量高斯变异操作。

设第k代的粒子j邻域极值数mj(k)满足：K1≤mj(k)＜K2，且粒子j位置为xj=(xj1,xj2,…xjN)，则可按下述过程对粒子j实施单变量高斯变异操作。

单变量高斯变异操的目的是依次对粒子j的位置向量xj的每一维分量进行扰动，以提高当前解的精度或找到比当前解更优的解。

3）当种群处于成熟期时，种群多样性和搜索能力均已丧失殆尽，此时种群中的粒子应逃逸种群，搜索新的可行区域。为此若粒子群中的粒子j的邻域极值数mj(k)＞K2，则对粒子j实施协同操作（协同操作将在下一节介绍），同时将以粒子j的位置为邻域极值的粒子初始化，使粒子具有新的动量对搜索空间进行新的搜索。

4 基于邻域极值数的协同粒子群优化算法及协同操作

基于邻域极值数的协同粒子群优化算法是将整个种群分为若干个独立进化子种群，并通过协同操作实现子种群间的信息交流共享、共同进化。协同操作借助基因库平台实现的。基因库可由每个子种群的第一代的最优粒子构成，也可以由各子种群进化一定代数后，每个种群最优粒子构成。协同操作过程如下。

设粒子群处于成熟期，粒子j的邻域极值数mj(k)＞K2，粒子j位置为xj=(x1,x2,…xN)，从基因库中随机地选取一个粒子，不妨选出粒子为t，其位置为yt=(y1,y2,…,yN)。

首先，由粒子j和选取的粒子t生成两个新粒子new1,new2，且新粒子new1，new2的位置xnew1,xnew2由式（7）确定

其中：l1,l2为1～N之间的随机整数，且l1＜l2。

当min{fitness(xnew1),fitness(xnew2)}＜fitness(xj)时，粒子j的位置xj用new1,new2中较优的粒子的位置替换；否则，粒子j的位置不变。上述操作可连续实施若干次，具体次数可由用户设定。

其次，基因库更新。为方便叙述基因库更新的过程，先给出粒子相似的定义。

定义5设粒子j的位置为xj=(x1,x2,…xN)，粒子t的位置为yt=(y1,y2,…,yN)，若位置向量的分量满足

其中：δ为一个很小的正数，则称粒子j,t相似。

将上一步操作得到的粒子j与基因库中的粒子逐一进行相似判断。若满足下面的条件①或②时，则对基因库进行更新；否则基因库不变。

①若粒子j与基因库的粒子t相似，且粒子j好于粒子t，则将粒子j替换基因库中的粒子t；

②若粒子j与基因库中粒子都不相似，且粒子j好于基因库中的最差粒子，则用粒子j替换基因库中最差的粒子。

基于以上的分析，基于邻域极值数的协同粒子群优化算法流程如下：

step1设定子种群数量及子种群规模，设置算法的最大迭代次数、优化精度；确定各子种群的粒子的初始位置及速度，邻域极值、全局极值；确定基因库，置迭代次数t:=0；

step2从第一个子种群开始直到最后一个子种群结束，各子种群依次完成step2.1、step2.2、step2.3三个步骤；

step2.1各子种群根据式（5）（6）对粒子进行速度和位置的更新，并更新粒子的邻域极值、全局极值；

step2.2对邻域极值数大于K1，小于K2的粒子进行单变量高斯变异操作，若变异后的粒子更优，则将变异后的粒子替换操作前的粒子，并更新以变异粒子的位置为邻域极值的粒子的邻域极值；

step2.3对邻域极值数大于K2的粒子实施协同操作，更新基因库，并将以该粒子为邻域极值的粒子初始化；

step3若算法的迭代次数t小于设定的次数，置t:=t+1，转step2；否则，输出基因库中的最好粒子的位置为所求问题的解。

5 仿真实验

5.1 测试函数

拟用4个经典的测试函数对算法的性能进行测试研究。测试函数如表1所示，其中函数f1,f2为单峰函数，函数f3,f4为多峰函数，4个测试函数的优化精度分别取0.05，100，0.5和100。

表1 测试函数Tab.1 Test functions

5.2 测试结果和性能分析

采用Matlab7.1实验平台进行仿真测试。算法1为本文提出的算法，算法2为文献［5］提出的CEPSO2算法。算法1参数的取值如表2所示。为了使测试数据的公平可信，算法2参数的取值尽可能与算法1保持一致。考虑到更新周期R是算法2的很重要的一个参数，当选取合适时，可大幅度提高算法2的收敛性。为此，更新周期采用文献［5］推荐的更新周期：R=30，且每隔一个更新周期记录全局最优值解。为了便于比较，算法1也每隔一个更新周期记录全局最优解。测试结果如表3所示，表中的MEAN、BEST、WORST、SD分别表示测试函数独立运行30次的实验结果的平均值、最好值、最差值和方差，SR表示达到优化精度的实验次数占总实验次数的比例。图1为各测试函数的收敛曲线。

表2 实验参数Tab.2 Parameter setting

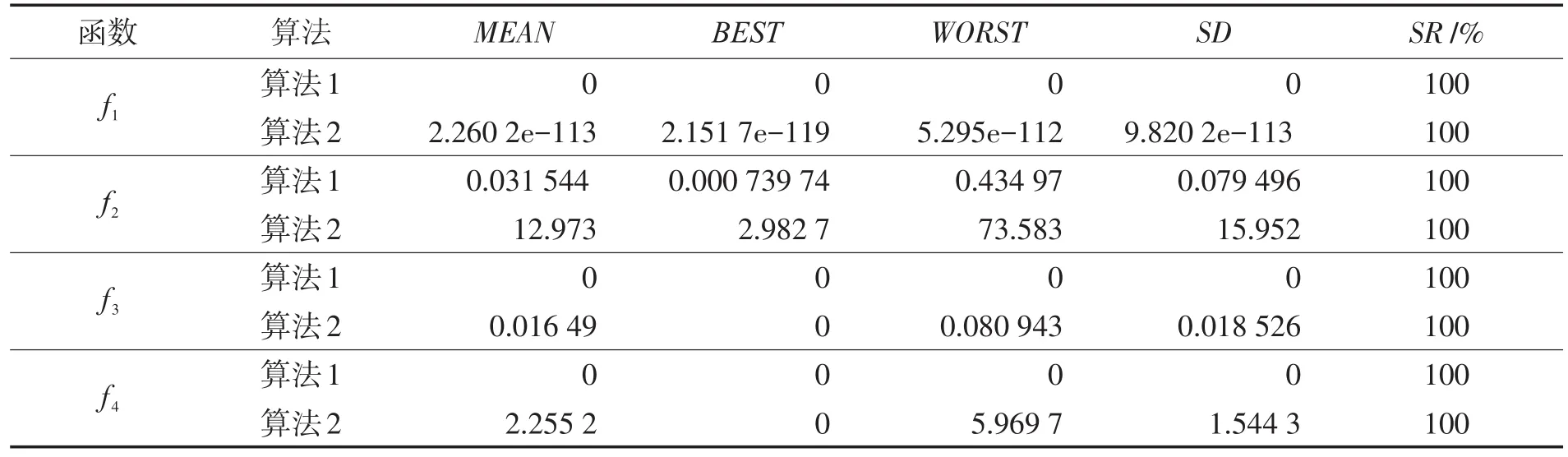
表3 2种算法仿真实验结果Tab.3 Two kinds of algorithm simulation results

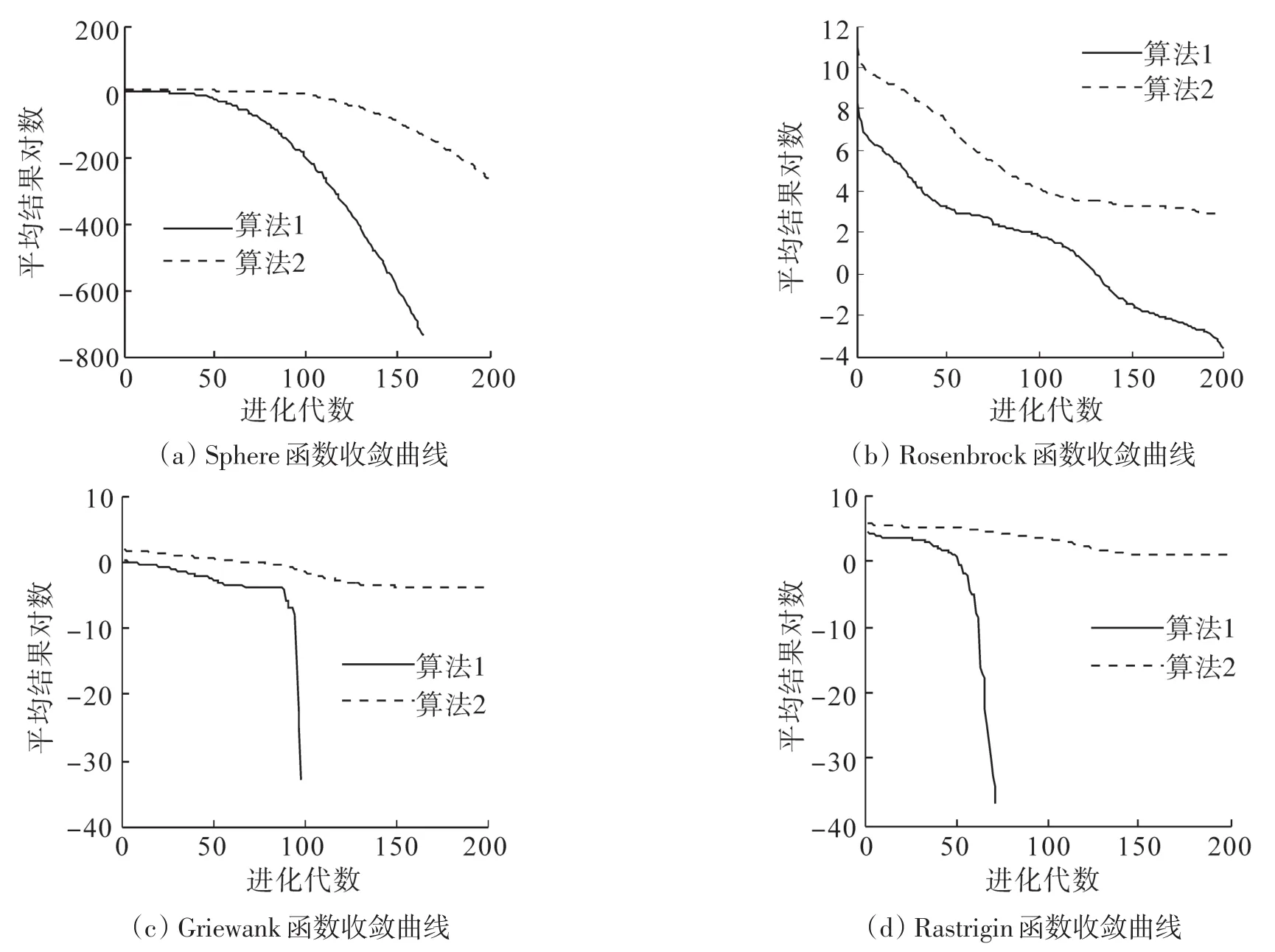
图1 测试函数收敛曲线Fig.1 Convergence curves of test function

从表3可以清楚地看出，算法1不仅实验结果的平均值好于算法2的，而且实验结果方差远比算法2的小，这表明算法1有较好鲁棒性。从图1的收敛曲线可明显地看出算法1有较快的收敛速度和较好的求解质量。另外，从两个多峰函数的收敛曲线看到，当算法2停滞不前进展缓慢时，而算法1却能持续进化获得满意解，这表明算法1不仅全局收敛速度快，而且收敛到全局最优解。

6 结束语

提出了基于邻域极值数的协同粒子群优化算法。该算法与同类的多种群协同粒子群优化算法有2个不同点：

1）利用种群邻域极值数确定种群的生存状态，根据子种群的生存状态对子种群实施相应的控制操作来提高子种群的搜索能力。这与以往利用种群多样性或搜索能力来判定种群的生存状态不同，是一种新的思路。

2）采用协同操作实现多种群的信息共享、共同进化。这与“孤岛模型”、“邻域模型”直接将搜索到的最优粒子“迁移”到子种群的方式不同。这保证了各子种群的独立进化，同时一定程度上避免了算法早熟收敛。

基本测试函数的测试结果表明基于邻域极值数的协同粒子群优化算法是一种高效稳健的全局优化算法，但在测试过程中发现参数K1,K2选择、单变量高斯变异次数和协同操作的次数都会对算法的性能产生一定的影响。

[1]KENNEDY J,EBERHART R.Particle swarm optimization[C]//Proc of the IEEE Int Conf Neural Networks,Piscataway,NJ,USA, 1995:1942-1948.

[2]倪庆剑,邢汉承,张志政.粒子群优化算法研究进展[J].模式识别与人工智能,2007,20(3):349-357.

[3]HIGASHI N,IBA H.Particle swarm optimization with gaussianmutation[C]//Proc of IEEE Swarm Intelligence Symposium(SIS), 2003:71-79.

[4]KUMAR J,ALMAGEED W A,DOERMANN D.Handwritten arabic text line segmentation using affinity propagation[C]//Proc.of the 9th IAPR International Workshop on Document Analysis Systems,New York,USA,2010:135-142.

[5]王元元,曾建潮,谭瑛.多种群协同进化的微粒群算法[J].计算机工程与设计2007,28(15):3661-3664.

[6]徐冰纯,葛洪伟,王燕燕.基于多种群多模型协同进化的粒子群优化算法[J].计算机工程2013(39):200-208.

[7]崔志华,曾建潮.微粒群优化算法[M].北京:科学出版社,2011:150-151.

[8]曾毅,朱旭生,廖国勇.一种基于邻域空间的混合粒子群优化算法[J].华东交通大学学报,2013,30(3):44-49.

[9]KENNEDY J,MENDES R.Population structure and performance[C]//Cec'02:Proceedings of the 2002 Congress on Evolutionary Computation,IEEE,Piscataway,NJ,USA,2002:1671-1676.

Cooperative Particle Swarm Optimization Based on Neighborhood Extremum Number

Zeng Yi,Zhu Xusheng,Liao Guoyong
(School of Basic Sciences,East China Jiaotong University,Nanchang 330013,China)

A cooperative particle swarm optimization based on the neighborhood extremum number is proposed.In this algorithm,the whole population is divided into several sub-populations evolving independently.The survival state of each sub-population is determined in terms of the neighborhood extremum number.Based on the survival state of each sub-population,corresponding control operation is implemented so as to improve the search ability of each sub-population and realize information sharing so that the sub-populations coevolve.The experimental re⁃sults show that the cooperative particle swarm optimization based on the neighborhood extremum number is an ef⁃fective and steady global optimization algorithm.

PSO;cooperative coevolution;the neighborhood extremum number

TP18

A

2014-04-07

国家自然科学基金项目（11161021）；华东交通大学校立科研项目（09111114）

曾毅（1965—），男，副教授，研究方向为智能计算。

1005-0523（2014）04-0071-06