Laplace变换在解微分方程中的应用研究
2014-07-20陆求赐
陆求赐
(武夷学院 人文与教师教育学院, 福建 武夷山 354300)
Laplace变换在解微分方程中的应用研究
陆求赐
(武夷学院 人文与教师教育学院, 福建 武夷山 354300)
本文阐述了Laplace变换在常微分方程与偏微分方程求解方面的应用,并对Laplace变换的应用进行了总结.
Laplace变换;常微分方程;偏微分方程
1 引言
与 Fourier变换法[4]一样,Laplace变换也是一种很重要的积分变换,它在工程技术、电路分析、天线、信号处理甚至天文学等方面都有重要的应用[1-3].同时 Laplace变换在 求解常微分方程、偏微分方程以及广义积分、反常积分等方面也都有着重要的应用[5-8].
我们在求解常微分方程时,可以利用 Laplace变换消去对自变量的求导运算,从而将常微分方程化成关于像函数的代数方程,然后再解出代数方程,最后求出 Laplace逆变换即可得出原常微分方程的解.这种方法也可用在求解偏微分方程的过程中,对于含有两个自变量的偏微分方程,在方程两端对其中一个自变量取 Laplace变换(一般为时间 t),可得到像函数关于另一个自变量的常微分方程,解出此方程,最后取逆变换,得到原问题的解,可极大地降低解题的难度.
本文首先给出 Laplace变换的定义与存在条件;文章第二部分说明如何利用 Laplace变换来求解常微分方程;第三部分通过例子说明如何利用 Laplace变换来求解偏微分方程;最后对 Laplace变换在求解微分方程中的应用进行总结.
下面先给出 Laplace变换的定义、存在定理与常用性质:
引理 1(Laplace变换存在定理) 如果函数 f(t)满足下面两个条件:(1)在 t≥0的任一有限区间上分段连续;(2)存在常数 M>0及 c≥0,使得 |f(t)|≤Mect(0≤t<+∞)成立;那么,f(t)的拉普拉斯变换在半平面 Re(s)>c内一定存在,且是解析的.
性质 1(微分性质)
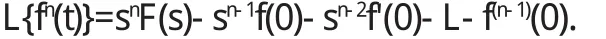
性质 2(卷积性质)
若 L{f(t)}=F(s),L{g(t)}=G(s),则
2 Laplace 变换在解常微分方程中的应用
利用 Laplace变换求解常微分方程的关键在于消去对自变量的求导运算,从而将常微分方程化成关于像函数的代数方程,在求 Laplace逆变换时可以按定义计算或者查Laplace变换表.下面说明如何利用 Laplace变换来求解一阶、二阶、k阶常微分方程.
2.1 一阶常微分方程的解法
这里只要结合 Laplace变换的微分性质及初始条件(2),式(1)可化为,则有

式(3)即为式(1)满足初始条件(2)的解的表达式.例1 解初值问题:
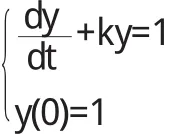
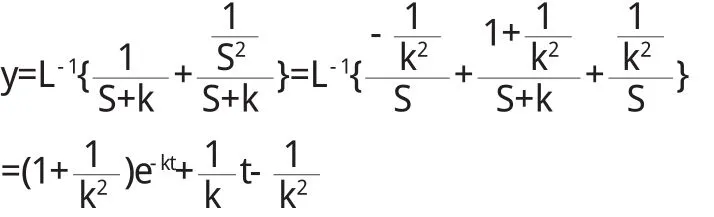
2.2 二阶常微分方程的解法
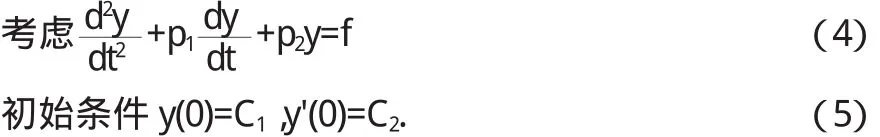
其中 y=y(t)为未知函数,f(t)为已知函数,p1,p2为常数.
这里只要结合 Laplace变换的微分性质及初始条件(5),式(4)可化为

其中式(6)中,H(S)=S2+p1S+p2,H0(S)=C1(S+p1)+C2,式(6)即为式(4)满足初始条件(5)的解的表达式.
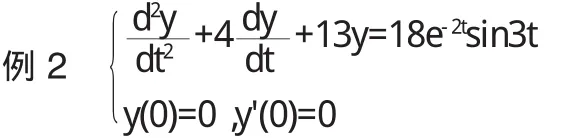
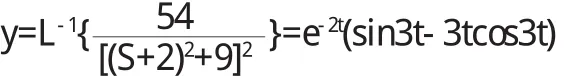
2.3 阶常微分方程的解法
其中 y=y(t)为未知函数,f(t)为已知函数,p1,p2,L,pn为常数.
这里只要结合 Laplace变换的微分性质及初始条件(8),可得式(7)的解为

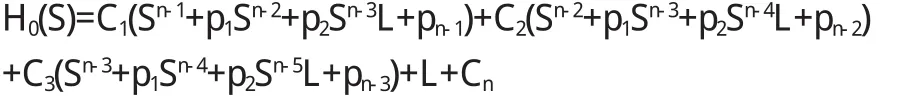
从以上的求解过程可以看出,利用 Laplace变换来求解常微分方程要比直接求解简单易行,而且在求 Laplace逆变换时可以查 Laplace变换表,这也极大简化了计算过程.另外,若是求解常微分方程组,也可类似地对每个常微分方程进行 Laplace变换,得到一个像函数的方程组,然后对每个方程取 Laplace逆变换即可[5].
3 Laplace 变换在解偏微分方程中的应用
Laplace变换可用来求解含时间变量的偏微分方程定解问题.比如含有变量 x和 t两个变量的偏微分方程定解问题,经过对时间变量 t进行变换后,就变为常微分方程(变量为 x)的定解问题了.然后利用 Laplace变换对此常微分方程(变量为 x)进行求解,并得到解的像函数,再对其进行反演,则可得到原问题的解.下面通过一个例子来进行说明:
例3 求无界杆的热传导问题
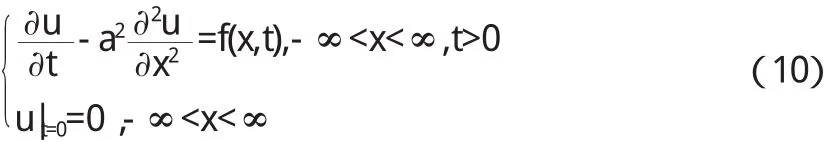
解 首先说明一下这里的边界 u|t=0=0,-∞ 此式为关于变量 x的常微分方程,根据文[2]例 11.11的结果,可以得到 再根据 Laplace变换的反演公式得, 最后再根据卷积定理,可得到原方程的解 从以上的求解过程可以看出,用 Laplace变换求解偏微分方程的定解问题,除了减少自变量的数目以外,某些已知函数的像函数(例如方程的非齐次项,它的形式可能很复杂)甚至都不必具体求出,在求反演时只需应用卷积定理即可. 综上可知,用 Laplace变换求解偏微分方程的步骤可归纳为:(1)对方程施行 Laplace变换,这一变换把初始条件也一并考虑了;(2)从变换后的方程解出像函数;(3)对求出的像函数进行反演,此时也可以查阅 Laplace变换表,所求的原函数就是原来方程的解. Laplace变换在解决常微分方程问题时,常微分方程经过变换,变成了代数方程,解出代数方程,再进行反演就能得到原常微分方程的解.在解决偏微分方程问题时,偏微分方程经过变换,变成了常微分方程,解出常微分方程,再进行反演就得到了原来偏微分方程的解.用 Laplace变换求解偏微分方程定解问题还有一个优点,就是不必将非齐次边界条件齐次化. 〔1〕潘祖梁,陈仲慈.工程技术中的偏微分方程[M].杭 州:浙江大学出版社,1995.139—150. 〔2〕吴崇试.数学物理方法[M].北京:北京大学出版社,1999. 〔3〕[美]罗纳德·N·布雷斯韦尔.傅里叶变换及其应[M].西安:西安交通大学出版社,2005.8.1-4. 〔4〕陆求赐.Fourier变换在求解半无界空间上波动方程中的应用[J].武夷学院学报,2014,33(2):50-53. 〔5〕施晓红.Laplace变换在求解线性微分及积分方程中的应用[J].昆明理工大学学报(理工版),2009,34(3):121-124. 〔6〕胡轶.浅析Laplace变换应用于初值问题[J].太原教育学院学报,2007,25(2).88-91. 〔7〕张洁萍,李俊林.关于Laplace变换及其性质的应用研究[J].太原科技大学学报,2010,32(3):249-251. 〔8〕唐妍霞.利用Laplace变换求解一维波动方程的定解问题[J].河北北方学院学报(自然科学版),2010,26(3):16-19. O175 A 1673-260X(2014)08-0003-02 武夷学院校科研基金资助项目(XL1204)
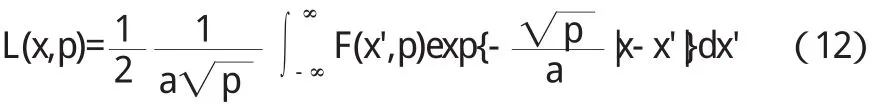
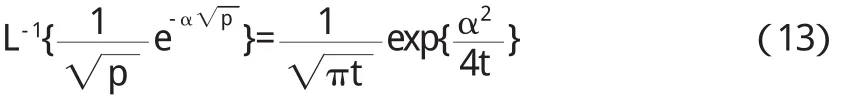
4 小结
