基于改进蚁群算法的机器人路径规划研究

万晓凤，胡伟，方武义，郑博嘉

南昌大学信息工程学院，南昌 330031

基于改进蚁群算法的机器人路径规划研究

万晓凤，胡伟，方武义，郑博嘉

南昌大学信息工程学院，南昌 330031

移动机器人是一个集环境监测感知、动态决策与规划、行为控制与执行等多功能于一体的复杂控制系统[1]。路径规划是机器人研究领域的一个关键环节，路径规划是指在有障碍物的环境中依据某些优化准则（如路径最短，最安全等），寻找一条从起始点到目标点之间安全无碰撞的最优或次最优路径[2-3]。国内外针对路径规划问题提出了很多算法，主要有可视图法、拓扑法、人工势场法等。随着智能算法的发展，神经网络算法、遗传算法、蚁群算法以及微粒群算法等也被广泛地应用于机器人路径规划当中[4]。

蚁群算法最早是作为一种解决组合优化问题的元启发式算法被提出，并成功地应用于旅行商问题。它采用分布式并行计算机制，有易与其他方法结合、鲁棒性较强等优点[5-6]。本文主要研究改进后的蚁群算法在机器人路径规划中的应用。

1 环境建模

本文所研究的机器人工作环境为二维静态空间，在描述障碍时采用把障碍物外扩一个机器人的最大直径，把机器人视作质点，在保障安全性的前提下简化问题的复杂度。由于栅格法地图表达规范，容易实现，并且其模型结构与旅行商问题类似，因此采用栅格法进行建模。

栅格法模型如图1所示，图中从左至右，从上至下对栅格进行编码。坐标以左下方位原点，从左到右为x轴正方向，从下到上为y轴正方向，每个栅格长度记为单位长度（假设为1 cm）。图中白色栅格为自由栅格，黑色栅格为障碍栅格，障碍不满一个栅格则填充满此栅格[7-8]。设栅格序号为c，n为每行每列的栅格数。图中序号编码与坐标对应关系如式（1）所示。

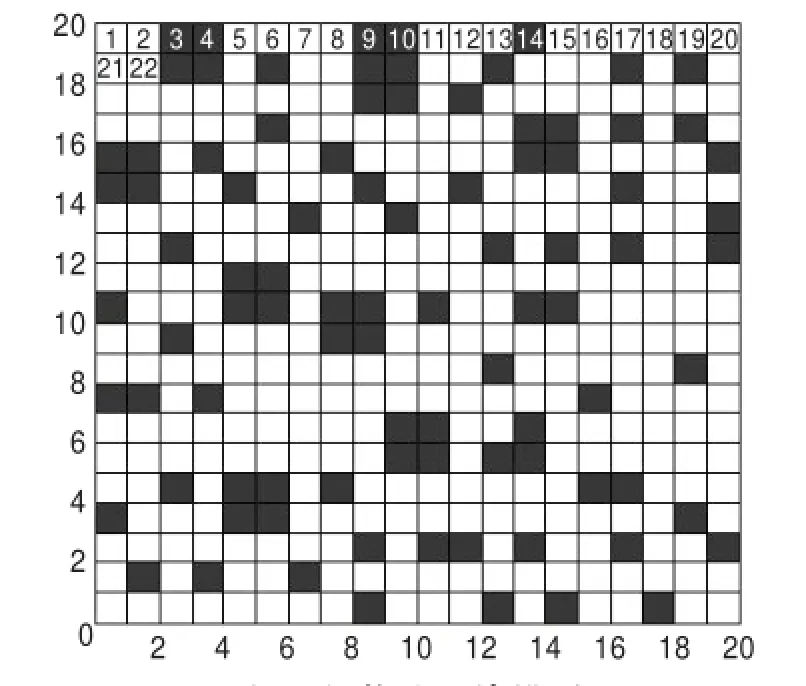
图1 栅格法环境模型

2 蚁群算法

2.1 基本蚁群算法

蚁群算法来源于自然界蚂蚁在寻找食物过程中发现路径的行为，为模拟自然界蚂蚁的行为，假设地图模型中出发点为蚁穴，目标点为食物源。整个路径规划过程可以看成是蚁群在地图中寻找食物的过程，蚂蚁间通过相互沟通、协调，最终避开障碍物找到一条最优路径。

现假设蚂蚁数量为M，栅格图规模为N×N，算法主要操作步骤如下：

（1）概率选择。蚂蚁根据公式（2），通过轮盘赌方法来选择将要前进的节点，Pm(i，j)是第m只蚂蚁从节点i到节点j的概率。τ(i，j)表示节点i至节点j边上的信息激素量，各条边的初始值为同一常数C。机器人只能向四周八个节点前进，Ji为节点i四周八节点中除去障碍节点及禁忌节点的集合，禁忌表TABUm存入蚂蚁已行节点。若蚂蚁陷入U型障碍，使得蚂蚁无后续节点选择，则默认该蚂蚁已经死亡，算法删除该蚂蚁及其所寻路径。η(i，j)表示ij两节点间的期望值，与两节点间距离成反比。α、β分别为信息激素和期望的启发因子[9]。

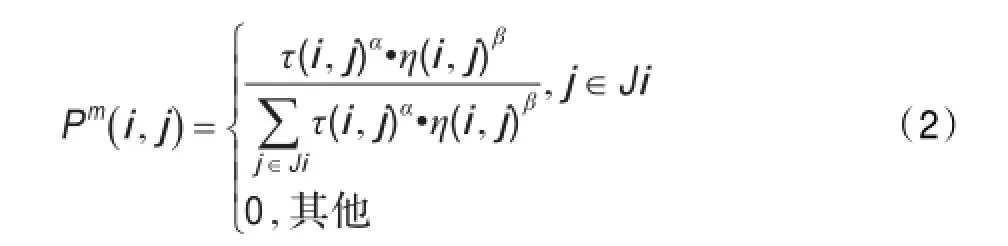
（2）信息激素量更新。每次所有蚂蚁寻迹完成后对信息激素进行全局更新，过去的信息激素量逐渐消逝，并加入新的信息激素量。更新规则如式（3）所示。参数ρ为挥发系数，一般取0～1之间常数。Tk(i，j)为k时刻节点ij间信息激素量，τk+1(i，j)为k+1时刻节点ij间信息激素量，Δτ(i，j)为本次循环节点ij间信息激素增量，由式（4）决定。式中Mij为经过路线ij的蚂蚁集合，Δτm(i，j)为第m只蚂蚁留给节点ij间的信息激素增量，由式（5）决定。Lm为第m只蚂蚁所寻路径的长度，Q为一适当正常数[10]。

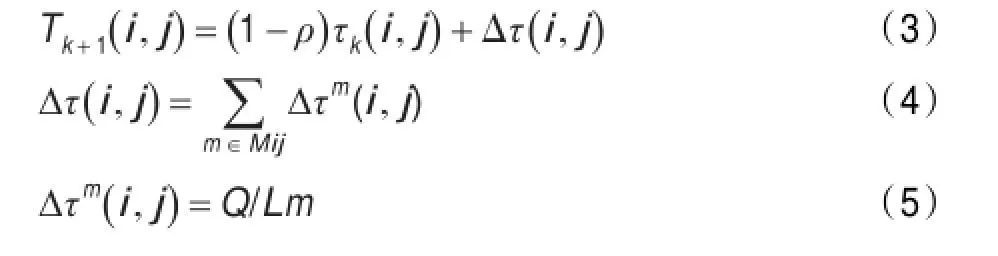
（3）迭代循环。每轮信息激素量更新完成后把所有蚂蚁再次放回起始点重新寻迹，经过K次迭代完成后，计算出最短路径。

2.2 改进蚁群算法

基本蚁群算法虽然能够规划出从起始点到目标点的路径，并有较强的鲁棒性，但依然存在很多不足，主要有容易过早停滞、搜索时间过长、效率较低等[11-12]。本文对基本算法做出几点改进，使得算法在更短时间内得出更短更平滑的路径。

（1）概率公式修改，修改期望值。由于基本蚁群算法期望值采用的是当前节点到下一个节点的距离反比函数，而这种情况下η(i，j)只有两个值，不利于蚂蚁选择下一个更优节点。而采用节点j到目标节点的距离来设定期望值，蚂蚁的所有下一个可行节点的期望值都是不同的，其中距离目标点最近的节点的期望值最大，这就使得蚂蚁更加倾向于选择离目标节点更近的节点，所寻路径长度也就更优。如式（6）所示，η(j，E)为节点j到目标节点的期望值，其值为1/LjE。

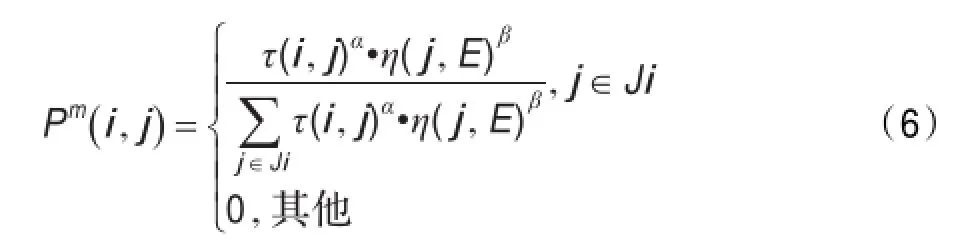
（2）信息激素更新规则修改，为使所寻路径更加平滑，节省机器人行走时间，加入拐点参数作为路径评价之一。机器人所寻路径中只有三种角，分别为锐角、直角、钝角，它们的值分别记为3、2、1，把所有角度值相加即得拐点参数值。由式（5）可知，在基本蚁群算法中，第m只蚂蚁经过ij段需增加的信息激素量为第m只蚂蚁所寻路径长度的反比函数，路径越长，增量越少[13]。而加入路径拐点参数按比例与路径长度相加，则可以利用这两个参数一起评价路径的优劣，由此决定需增加的信息激素量，使所寻路径长度优且更加平滑。如式（7）所示，GDm为第m只蚂蚁所寻路径的拐点参数，λ为加权系数。

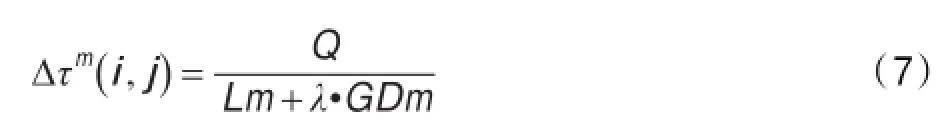
（3）挥发系数采用自适应方式，由于蚂蚁未走过的路径因信息激素的衰减而降低被选择的概率，影响算法的全局搜索能力，若ρ过小，会降低算法的收敛速度，而ρ过大则会影响算法随机性和搜索能力[14-15]。当经过若干次迭代后最优路径无改进时，采用式（8）更新挥发系数，本文γ=0.85。

2.3 改进蚁群算法流程

应用改进蚁群算法进行路径规划的具体步骤如下：

（1）构建环境模型，初始化各参数，设置最大迭代次数K，k=1，m=1。

（2）把蚂蚁m(m=1，2，…，M)放到初始位置，并把初始点加入禁忌表TABUm中。

（3）根据概率公式（6）使当前蚂蚁m转移至下一节点，并修改禁忌表，如此循环，直到蚂蚁到达目标节点。若中途蚂蚁落入U型陷阱，无下一节点可走，则判断此蚂蚁死亡。

（4）存储当前蚂蚁m的所寻路径及路径长度，删除死亡蚂蚁，默认其路径长度为无穷大。m=m+1，若m＜M，回到（2）。

（5）按信息激素更新公式（3）、（4）及（7）进行全局信息激素更新。迭代次数k=k+1，若k＜K，则m=1继续（2）循环。

（6）算法结束，输出最优路径。

3 仿真分析

为验证改进后算法的有效性，现使用软件MATLAB7.0对基本蚁群算法和改进蚁群算法进行仿真，并比较它们的仿真结果。

机器人的环境模型如图1所示，各参数设置分别为：α=1，β=2，M=100，N=20，K=200，ρ=0.2，Q=2 000，λ=2，γ=0.85。基本蚁群算法和改进蚁群算法寻优结果分别如图2和如图3所示。多次运行两种算法，比较它们的最优路径及迭代情况，结果如表1所示。

通过图2和图3两种算法寻优结果可以直观地看出基本算法所寻路径长，拐点参数大。而改进后算法所寻路径长度大大减小，且平滑度好。

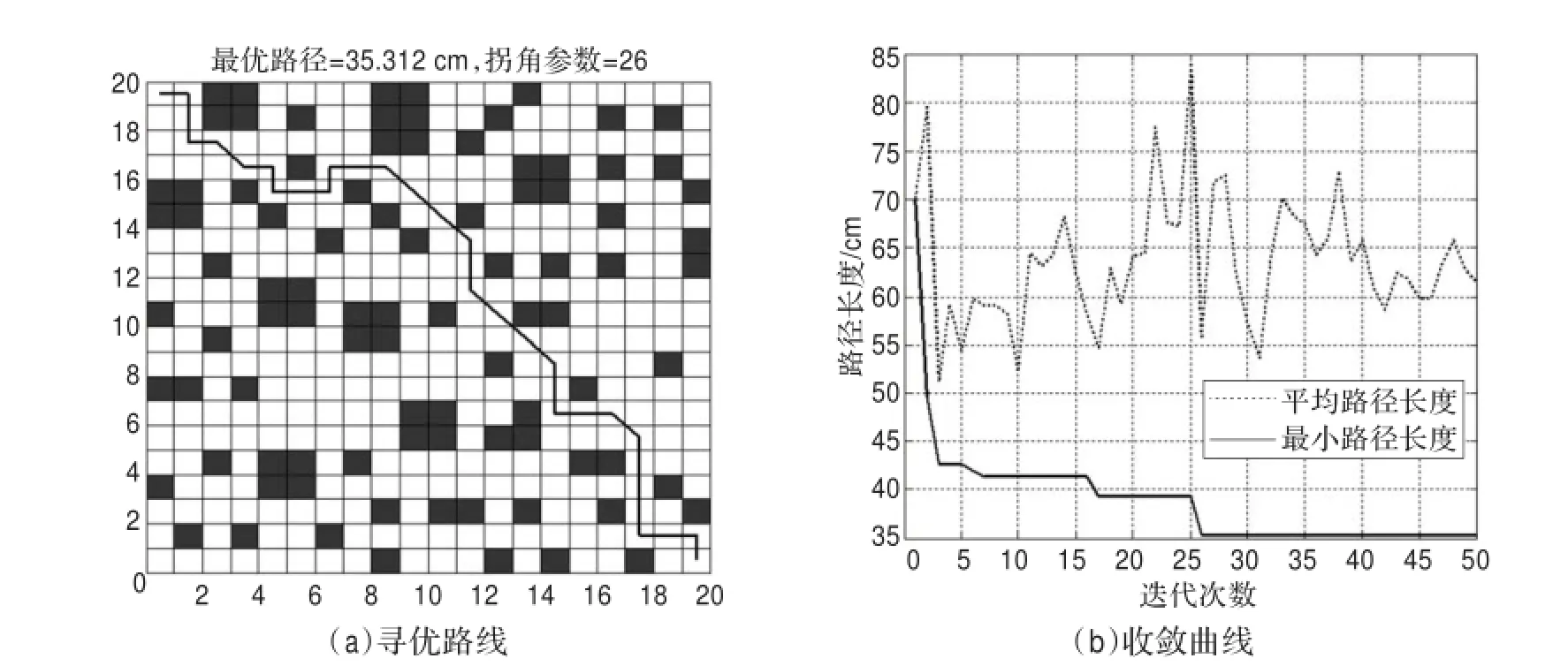
图2 基本蚁群算法仿真结果

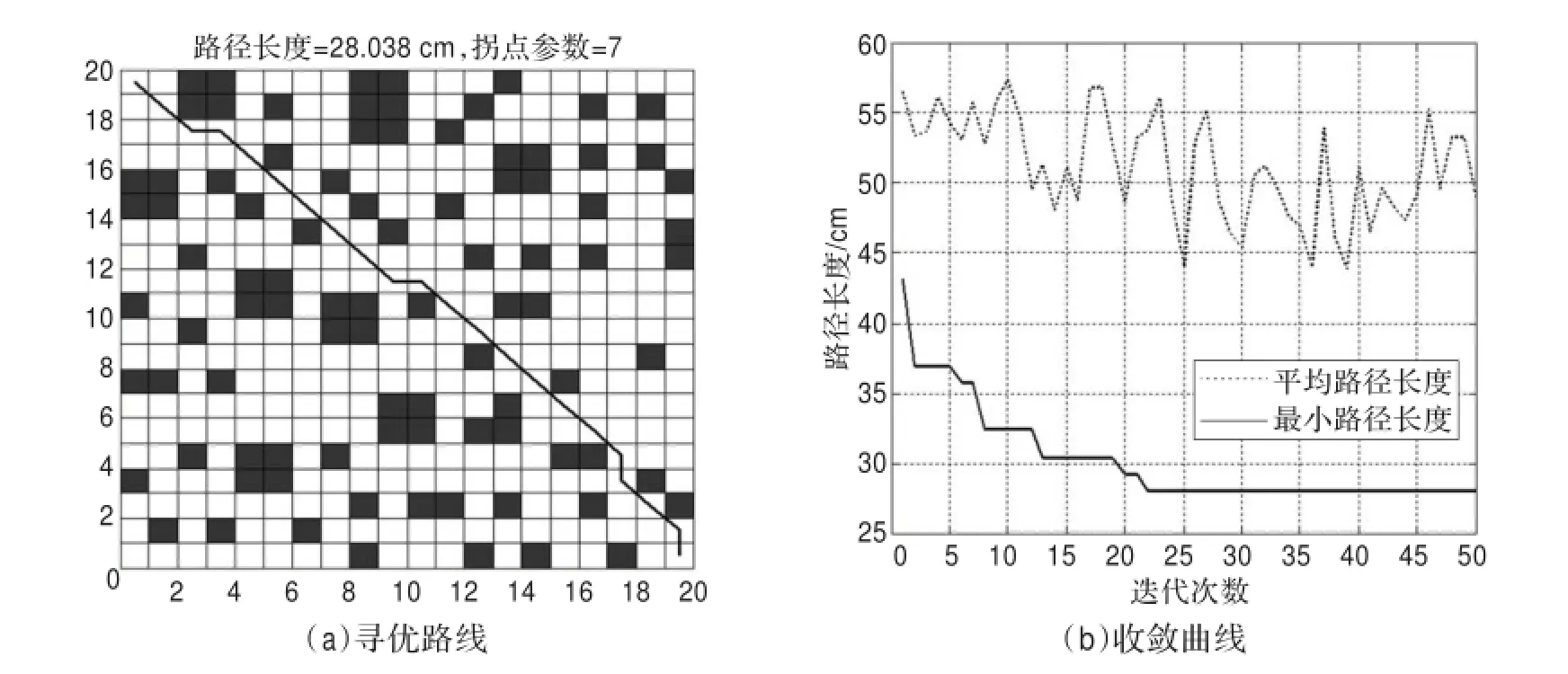
图3 改进蚁群算法仿真结果

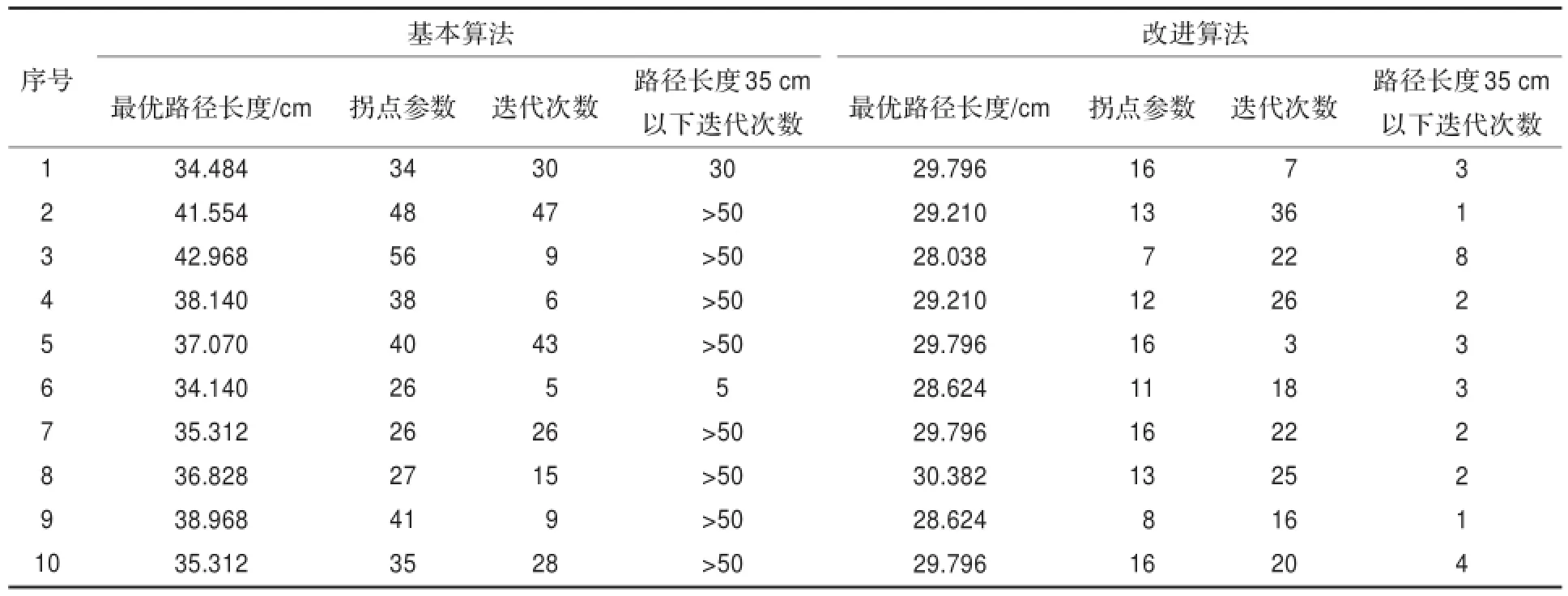
表1 基本算法与改进算法多次运行结果比较

对比表1数据，首先，基本蚁群算法中，最优路径长度远大于改进蚁群算法最优路径长度，拐点参数也远大于改进蚁群算法。十次运行结果中，基本蚁群算法只有两次最优路径达到35 cm以下，最小拐点参数为26；而改进后算法只有一次最优路径在30 cm以上，最大拐点参数也只有16，并且找到了本文地图环境下实际最优路径，其长度为28.038 cm，拐点参数为7。说明改进后算法所寻路径大大优于基本算法。

其次，从迭代次数看，虽然终值迭代次数改进算法和基本算法看起来优势不大，但是基本算法很难在50次迭代内寻到长度35 cm以下的路径。说明基本算法搜索速度慢，算法过早停滞，易陷入局部最优。而改进后算法很快就能搜索到长度35 cm以下路径，在5次迭代之内基本就能完成，并且还能继续快速搜索到最优路径。这说明改进后算法收敛速度快，搜索能力强。

分析结果得出，基本蚁群算法搜索能力弱，寻优效果差，效率较低。而改进后的蚁群算法搜索能力增强，收敛速度快，效率高，寻优效果好，机器人可以快速地避开障碍物安全到达目标点。

4 结论

本文针对基本蚁群算法在机器人路径规划中的不足，对算法做出改进。加入目标点吸引机制，让机器人更加趋近于目标点移动。挥发系数自适应，改善蚁群算法的性能。拐点参数评价有效地改善了路径的平滑度。通过对仿真结果的分析，得出改进后的蚁群算法能够有效地弥补基本蚁群算法的不足，算法搜索速度加快，所寻路径更短且更平滑，大大提高了机器人的效率。

本文主要研究了机器人在二维静态空间内的路径规划，环境信息完全已知，虽取得了较好的结果，但算法设计上仍有不足之处有待改进。在接下来的研究中，应当更加深入地研究此算法，并且考虑机器人在动态环境下障碍探测以及扩展到三维空间内的路径规划问题。

[1]Soulignac M.Feasible and optimal path planning in strong current fields[J].IEEE Transactions on Robotics，2011，27（1）：89-98.

[2]刘华军，杨静宇.移动机器人运动规划研究综述[J].中国工程科学，2006，8（1）：85-94.

[3]王娟，吴宪祥.基于改进粒子群优化算法的移动机器人路径规划[J].计算机工程与应用，2012，48（15）：240-244.

[4]李学洋，李悦，张亚伟.基于遗传变异蚁群算法的机器人路径规划的改进[J].电子设计工程，2012，20（15）：38-40.

[5]段海滨，王道波.蚁群算法理论及应用研究的进展[J].控制与决策，2004，19（12）：1321-1326.

[6]Dorigo M，Caro G D.Ant colony optimization：a new meta-heuristic[C]//Proceedings of the 1999 Congress on Evolutionary Computation，1999：1470-1477.

[7]朱磊，樊继壮.基于栅格法的矿难搜索机器人全局路径规划与局部避障[J].中南大学学报：自然科学版，2011，42（11）：3421-3428.

[8]罗荣贵，屠大维.栅格法视觉传感集成及机器人实时避障[J].计算机工程与应用，2011，47（24）：233-235.

[9]蔡荣英，王李进，吴超.一种求解旅行商问题的迭代改进蚁群优化算法[J].山东大学学报：工学版，2012，42（1）：6-11.

[10]吴华锋，陈信强，毛奇凰.基于自然选择策略的蚁群算法求解TSP问题[J].通信学报，2013，34（4）：165-170.

[11]Xiong W，Wei P.A kind of ant colony algorithm for function optimization[C]//Proceeding of the 1st International Conference on Machine Learning and Cybernetics，Beijing，2002：552-555.

[12]周明秀，程科，汪正霞.动态路径规划中的改进蚁群算法[J].计算机科学，2013，40（1）：314-316.

[13]王越，叶秋冬.蚁群算法在求解最短路径问题上的改进策略[J].计算机工程与应用，2012，48（13）：35-38.

[14]徐瑾.基于改进蚁群算法的移动机器人路径规划研究[D].河北保定：华北电力大学，2011.

[15]陈一昭，姜麟.蚁群算法参数分析[J].科学技术与工程，2011，11（36）：9080-9084.

WAN Xiaofeng,HU Wei,FANG Wuyi,ZHENG Bojia

College of Information Engineering,Nanchang University,Nanchang 330031,China

The basic ant colony algorithm applied to robot path planning in the two-dimensional static environment has problems of long search time,inefficiency and easy to fall into local optimization and so on.It makes improvements on the algorithm for these problems.It uses different expectation mechanism,updates the pheromone by taking evaporation coefficient adaptive approach,and joins the inflection point parameter as one evaluation criteria of the path.Simulation of the two algorithms shows the improved ant colony algorithm is stronger of searching ability and more efficient than the basic ant colony algorithm and gets a shorter path.The results show that the improved algorithm improves the efficiency of the algorithm and inhibits algorithm into local optimum and achieves search of robot’s optimal path.Robot can avoid obstacles to reach the target point safely and quickly.

ant colony algorithm;path planning;evaporation coefficient adaptive;inflection point parameter;optimal path

在二维静态环境下的机器人路径规划中，采用基本蚁群算法寻优存在搜索时间较长、效率较低、容易陷入局部最优等问题。针对这些问题对基本蚁群算法进行改进，改进的蚁群算法使用不同的期望值机制，采用挥发系数自适应方式更新信息激素，并加入拐点参数作为路径的评价标准之一。对这两种算法进行仿真分析，可得改进后的蚁群算法比基本蚁群算法搜索能力更强，算法效率更高，所寻路径更短。结果表明，该改进算法提高了算法效率，抑制了算法陷入局部最优并实现了机器人最优路径搜索，使机器人可以快速地避开障碍物安全到达目标点。

蚁群算法；路径规划；挥发系数自适应；拐点参数；最优路径

A

TP18；TP24

10.3778/j.issn.1002-8331.1311-0106

WAN Xiaofeng,HU Wei,FANG Wuyi,et al.Research on path planning of robot based on improved ant colony algorithm.Computer Engineering and Applications,2014,50（18）：63-66.

江西省科技支撑项目（No.20133BBE50029）；江西省科技厅工业支撑计划（No.20132BBE50049）。

万晓凤（1964—），女，教授，从事计算机控制与嵌入式智能仪表研究。E-mail：xfwan_jxw@163.com

2013-11-11

2013-12-30

1002-8331（2014）18-0063-04

CNKI网络优先出版：2014-04-01,http://www.cnki.net/kcms/doi/10.3778/j.issn.1002-8331.1311-0106.html