一类活化基质模型非常数正平衡解的全局结构

魏美华，常金勇，马崛

1.榆林学院数学与统计学院，陕西榆林 719000

2.中国科学院信息工程研究所，北京 100093

一类活化基质模型非常数正平衡解的全局结构

魏美华1，常金勇2，马崛1

1.榆林学院数学与统计学院，陕西榆林 719000

2.中国科学院信息工程研究所，北京 100093

1 引言

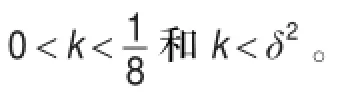
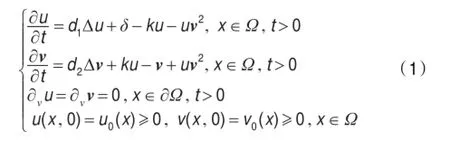
对于该活化基质模型的研究工作主要集中在从常微分方程角度讨论极限环的存在性和唯一性[8-10]。关于已有常微分方程结果，文献[8-9]运用数值和实验方法说明了极限环的存在性，我国陈兰荪先生[10]运用常微分方程理论数学上严格地证明了极限环的存在性和唯一性。考虑到反应物分子扩散的情况，这涉及到偏微分方程。而关于已有的偏微分方程结果，文献[11]讨论了常数平衡解的存在性和稳定性，而运用拓扑度理论和解的先验估计研究了非常数平衡解的存在性和不存在性[12]。

在此基础上，本文在一维空间下运用分歧理论和度理论研究该模型非常数平衡解的局部和全局结构，运用数值模拟给予解释和验证，并阐明该模型具有活化基质模型所具有的本质特征。所得理论分析结果推广了文献[13]。

2 预备知识

引理2表明若d1比较小或d2比较大时，方程（1）没有非常数正解。

假设条件：

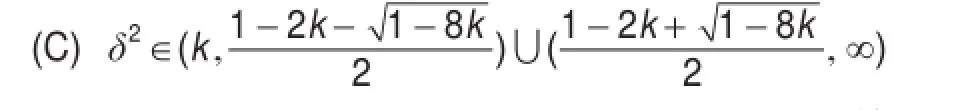
成立。它是该糖酵解模型为活化基质模型以及常数平衡解无扩散稳定的充分条件。

3 局部分歧

本章在一维空间Ω=(0，l)，l＞0下，以d1作为分歧参数运用分歧理论分析式（1）的非常数平衡解的局部结构。

在一维情况下，系统式（1）的平衡解相应于系统：的特征值λj=(πj/l)2，j=0，1，…，相应的正规化的特征函数为：

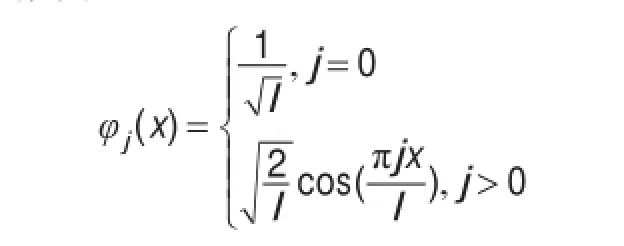
则{φj(x):j=0，1，…}构成L2(0，l)的一组标准正交基。设Hilbert空间Y=L2(0，l)×L2(0，l)的内积为：

考虑L的伴随算子：

4 全局分歧

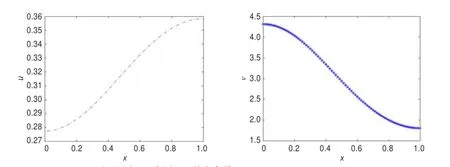
图1 模型式（1）的非常数平衡解

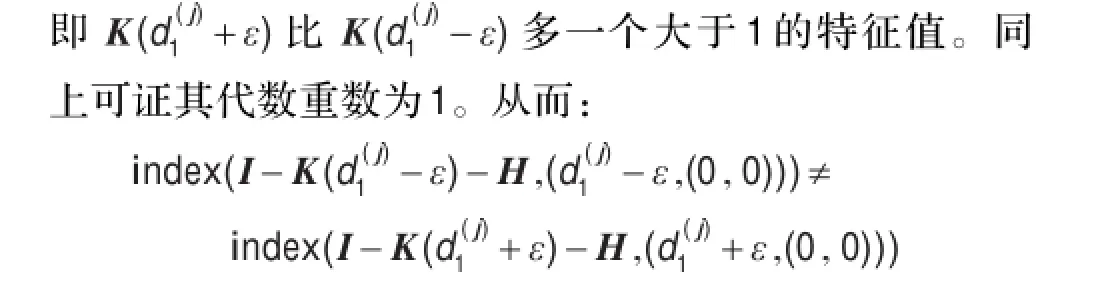
设Uˉ是系统式（6）的解，则可利用反射和周期延拓构造系统式（3）的解：

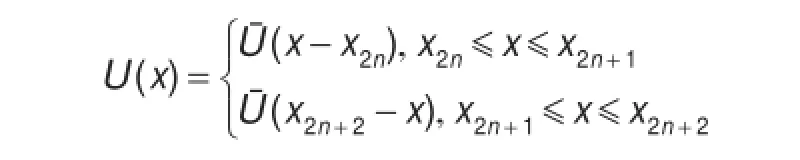
易知(，(0，0))是系统式（6）的分歧点。同理可证系统式（6）的分歧曲线要么延伸到无穷，要么连接((0，0))，k′＞k。若第二种情况发生，则与k的定义矛盾，所以Γˉk延伸到无穷。综上可知，Γj延伸到无穷。而由引理1知u是有界的，因此Γj随延向无穷。

注2定理2说明Γj不会最终连接到某个分歧点，但是有可能Γj连接某个分歧点并最终延向无穷。

注3图1刻画了非常数平衡解的存在性，证实了定理1和定理2。图2体现了活化基质模型的本质特征，即活化剂越多则基质越少，这是因为活化剂越多会导致基质的消耗越多。

5 结束语

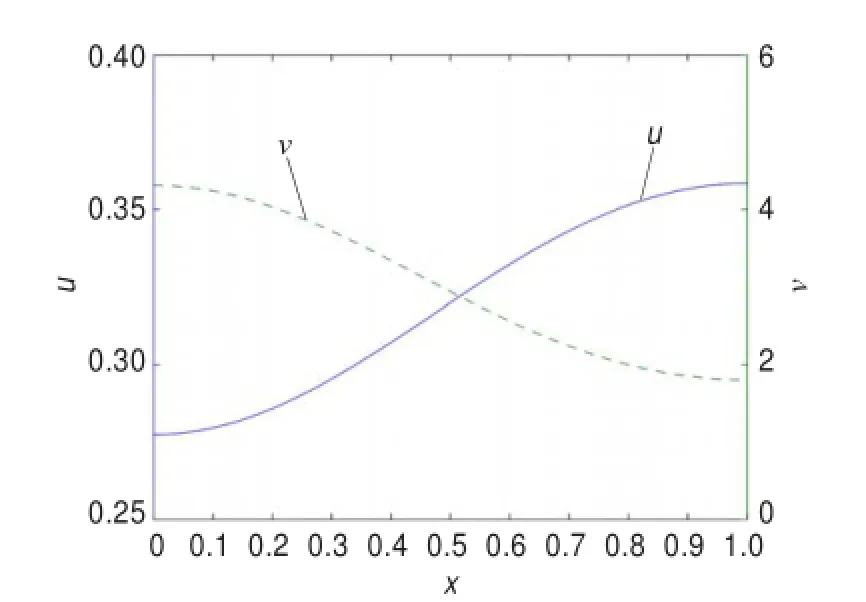
图2 基质u和活化剂v的对比

基于已有的工作，参见文献[12]，为了进一步讨论带Neumann边界条件的活化基质模型（即糖酵解模型）正平衡解的存在性，本文在一维空间上以扩散系数d1为分歧参数，运用局部和全局分歧理论以及度理论研究了该模型常数平衡解产生的局部分歧解结构和全局分歧解走向，并利用数值模拟得以验证，所得结果证实了图灵模式的形成。

[1]Turing A M.The chemical basis of morphogenesis[J].Phil Trans R Soc London Ser B，1952，237：37-72.

[2]Murray J D.Mathematical biology II：spatial models and biomedical applications[M].3rd ed.[S.l.]：Springer，2003.

[3]叶其孝，李正元.反应扩散方程引论[M].北京：科学出版社，1994.

[4]Ni W M，Kanako S，Izumi T.The dynamics of a kinetic activator-inhibitor system[J].J Differential Equations，2006，229：426-465.

[5]Wei J，Winter M.Existence，classification and stability analysis of multiple-peaked solutions for the Gierer-Meinhardt system inR1[J].Methods Appl Anal，2007，14：119-163.

[6]Hale J K，Peletier L A，Troy W C.Exact homoclinic and heteroclinic solutions of the Gray-Scott model for autocatalysis[J].SIAM J Appl Math，2000，61：102-130.

[7]Li Y.Steady-state solution for a general Schnakenberg model[J].Nonlinear Anal RWA，2011，12（4）：1985-1990.

[8]Tyson J，Kauffman S.Control of mitosis by a continuous biochemical oscillation[J].J Math Biol，1975，1：289-310.

[9]Segel L A.Mathematical models in molecular and cellular biology[M].Cambridge：Cambridge University Press，1980.

[10]陈兰荪，王东达.一个生物化学反应的振动现象[J].数学物理学报，1985（3）：261-266.

[11]Ashkenazi M，Othmer H G.Spatial patterns in coupled biochemical oscillators[J].J Math Biol，1978，5：305-350.

[12]魏美华，吴建华.一类糖酵解模型正平衡解的存在性分析[J].数学学报，2011（4）：553-560.

[13]Jang J，Ni W M，Tang M.Global bifurcation and structure of turing patterns in 1-D Lengyel-Epstein model[J]. J Dynam Differential Equations，2005，16：297-320.

[14]Crandall M，Rabinowitz P.Bifurcation from simple eigenvalues[J].J Functional Anal，1971，8：321-340.

[15]Wei M H，Wu J H，Guo G H.Turing structures and stability for the 1-D Lengyel-Epstein system[J].J Math Chem，2012，50：2374-2396.

[16]Rabinowitz P H.Some global results for nonlinear eigenvalue problems[J].J Functional Anal，1971，7：487-513.

WEI Meihua1,CHANG Jinyong2,MA Jue1

1.School of Mathematics and Statistics,Yulin University,Yulin,Shaanxi 719000,China
2.Institute of Information Engineering,Chinese Academy of Sciences,Beijing 100093,China

An activator-substrate system under Neumann boundary condition is considered in one-dimensional space.Taking the diffusion coefficientd1as bifurcation parameter,the local and global bifurcation of constant steady-state solution are studied by bifurcation theory and degree theory.Moreover,the theoretical results are confirmed by numerical simulations, and also continue the previous work.It is shown that the nonconstant steady-state branches join up with infinity.

activator-substrate model;bifurcation;steady-state solutions;global structure

在一维空间上，研究一类带Neumann边界条件的活化基质模型。以扩散系数d1为分歧参数，运用分歧理论和度理论研究该模型常数平衡解的局部分歧和全局分歧，利用数值模拟得以证实。理论结果表明非常数平衡解分支延伸向无穷，这是已有工作的继续。

活化基质模型；分歧；平衡解；全局结构

A

O175.26

10.3778/j.issn.1002-8331.1402-0295

WEI Meihua,CHANG Jinyong,MA Jue.Global structure of nonconstant steady-state solutions for activator-substrate system.Computer Engineering and Applications,2014,50（18）：50-53.

国家自然科学基金（No.11271236）；陕西省教育厅科研计划资助项目（No.14JK1862）；榆林学院博士科研启动基金项目（No.13GK04）。

魏美华（1981—），女，博士，讲师，主要研究方向为偏微分方程及其可视化；常金勇（1982—），男，博士生，讲师；马崛（1981—），女，讲师。

2014-02-26

2014-05-30

1002-8331（2014）18-0050-04

CNKI网络优先出版：2014-07-25，http://www.cnki.net/kcms/detail/10.3778/j.issn.1002-8331.1402-0295.html