基于神经网络模型的双混沌 Hash 函数构造

刘 慧赵 耿白 健

1(西安电子科技大学通信工程学院 西安 710071)2(北京电子科技学院 北京 100070)

基于神经网络模型的双混沌 Hash 函数构造

刘 慧1,2赵 耿1,2白 健1,2

1(西安电子科技大学通信工程学院 西安 710071)2(北京电子科技学院 北京 100070)

高效快速的单向 Hash 函数是当前安全技术研究的热点。文章采用神经网络结构构造了一种 Hash 函数，由 Logistic 映射和 Chebyshev 映射结合起来的双混沌系统产生该神经网络的参数，将明文信息逐块进行处理，并最终通过异或产生 128 bit 的 Hash 值。经实验数据和仿真分析可知：文章提出的方案满足单向 Hash 函数所要求的混乱和置换特性，并且具有很好的弱碰撞性和初值敏感性；另外，该方案结构简单容易实现。

双混沌系统；Hash 函数；神经网络；Logistic 映射；Chebyshev 映射

1 引 言

随着电子商务的迅速发展，单向 Hash 函数在以公钥密码技术、数字签名、完整性验证、身份认证和动态口令鉴别等为代表的安全技术中得到了广泛的应用[1,2]。传统的单向 Hash 方法有MD2、MD5 和 SHA 等标准[3,4]，但它们多数基于复杂度假设，需要进行大量复杂的异或等逻辑运算[5,6]。近年来，利用混沌系统的确定性和对初值的敏感性来构造密码算法已经成为国内外研究的热点[7-9]。其中，基于混沌的 Hash 函数能很好地解决传统 Hash 函数运算量的问题，但是基于单一混沌系统的 Hash 函数构造的方案还存在一些不足：基于某些特定混沌系统来实现的 Hash 函数的构造可以利用各种混沌预测技术成功地破译和提取信号[10]，保密性能并非完美，而且在实际实现过程中受处理器字长精度的限制，混沌映射本身所产生的混沌序列也会退化为周期序列[11]。为了避免出现上述弊端，充分发挥混沌映射的优点，本文采取将两种混沌映射结合在一起产生系统参数的构造方法，并且将混沌系统产生的参数在使用中与明文相结合进行不断地更新，避免出现混沌映射逐渐退化成为周期序列的弊端。理论分析和实验仿真证明，本文提出的方案具有很好的混乱置换特性和弱碰撞性，具有扩展研究的实际意义。

2 预备知识

在本节中就本文所用到的基本知识进行介绍，以便在下述小节中进行 Hash 函数的构造。

2.1 Logistic 映射

一维 Logistic 映射从数学形式上来看是一个非常简单的混沌映射，它具有极其复杂的动力学行为，运算速度快，方程反复迭代可以产生较好的混沌序列，而产生的混沌序列对初始状态和系统参数极其敏感，在保密通信领域中的应用十分广泛，其数学表达公式如下：

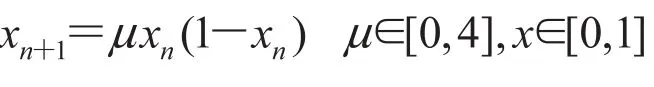
图 1 Logistic 映射的分叉图Fig. 1. The diagram of Logistic map bifurcation

2.2 Chebyshev 映射

Chebyshev 映射是一种简单却十分有效的以阶数为参数的混沌序列映射。令 Tn(x)＝cos(n. cos—1(x))，则 Tn(x)称为 n 阶第一切比雪夫多项式(Chebyshev)。它有下列性质：

图 2 Chebyshev 多项式(T0—T4)的图象Fig. 2. The diagram of Chebyshev polynomials

3 双混沌系统 Hash 函数的构造方法

3.1 双混沌系统的构造方法

从混沌映射中生成的混沌序列有实值序列和二值序列两种。前者是混沌映射轨迹点集合的子集形成的序列。后者通过定义一个阈值，从实数值的混沌序列中得到。本文的双混沌系统产生的混沌序列是一个实值序列。

分别用 Logistic 映射与 Chebyshev 映射，各自通过迭代得到一组混沌实值序列，将这两个新序列按位异或，形成一组新的序列。新序列也是一个实值序列，也具有相应的混沌特性[12]。混沌序列产生的原理图如图 3。

3.2 单向 Hash 函数的整体构造

本文设计的 Hash 函数方案首先将明文进行填充并分块，每次处理明文的256 比特，将每次得到的 Hash 值迭代到系统神经网络的参数矩阵中，从而保证每块明文得到的 Hash 值都能与前面所有的参数和明文相关，以保持系统的初值敏感特性。最终的 Hash 值则是所有明文块 Hash 值的异或。本算法的整体框架图如图 4 所示。

本方案的具体设计步骤：

图 3 双混沌系统的构造原理图Fig. 3. The construction of double chaotic maps

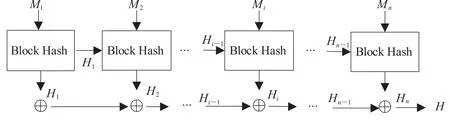
图 4 本文 Hash 算法的整体设计框架Fig. 4. The construction of our Hash function

(1)首先选取适当的参数，通过双混沌系统进行迭代(注意该参数必须满足使得迭代后产生的值满足混沌特性)，从至少 500 次以后开始取出迭代值记为 X1, X2,…, X512，将这 512 个迭代值按顺序排列作为神经网络中的参数。其中X1, X2,…, X256作为第一个矩阵 A 的初始值，X257, X258,…, X512作为第二个矩阵 B 的初始值。其中， A 矩阵需要不断的通过输出进行更新，在第四步中我们将会给出详细的更新规则。

(2)将待 Hash 的明文进行填充，将其填充成 256 bit 的整数倍，填充方法和现行的 SHA-3 类似，主要是为了方便明文块处理，每次均以256 bit 进行处理。将填充后的明文进行分组 M1, M2,…, MN, Mi为 256 bit。

(3)输入 256 bit 作为一块明文 Mi。将其分为m1, m2,…, m16，mi(i＝1,2,…,16)，每一个 mi是 16 bit，将其除以 216，变成 0～1 之间的小数，记为。

(4)将明文块 Mi进入神经网络的单元，即对进行如下操作：

注意：为了避免混沌序列由于计算机精度的影响进入周期循环，在此对矩阵 A 进行不断地更新。更新方法是将每次第二步产生的结果 y1, y2,…, y16代入 A 中，使得 A 中所有的列均向右移动一列，最右边一列舍弃，这样 A 矩阵的第一列便被替换为 {y1, y2,…, y16}T。

4 对于 Hash 函数的有效性分析

4.1 文本 Hash 结果

取初始文本为“If I were a boy again and gentle as courage, nothing so cruel and pitiless as cowardice,” says a wise author. We too often borrow trouble, and anticipate that may never appear.” He fear of ill exceeds the ill we fear.”dangers will arise in any career, but presence of mind will often conquer the worst of them. Be prepared for any fate, and there is no harm to be feared. If I were a boy again, I would look on the cheerful side, life is very much like a mirror if you smile upon it, it smiles back upon you; but if you frown and look doubtful on it, you will get a similar look in return.”文本 1 将文本中的 If 变成 1f，文本 2 将文本中的 feared 改成 freaed，文本 3 将文本 again后面的“,”改成“.”。文本 4 将文本中的 upon改成 on。5 个文本的 Hash 结果用 16 进制表示结果如下：

原文本：81CAFD161CEDFDE44D3D7BB40A2E FD17

文本 1：1B2FC1BE6B94AFBD4740D76D9F9B8449

文本 2：98B8C56C7B33F8153A4C06E6A173669F

文本 3：50EFD2AC96C78A123E52538A4429E49B

文本 4：B82FFFDCEC4097556998B0ABC8A08563

用 0,1 序列的图形化表示，如图 5 所示。

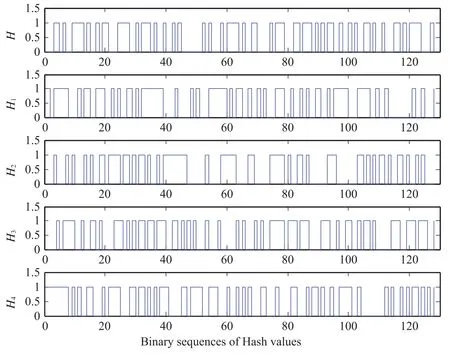
图 5 5 次 Hash 值的 0,1 序列图形Fig. 5. The fi ve Hash values of sequence on 0 bit and 1bit

4.2 Hash 值的混乱与扩散性质的统计分析

为了隐藏明文消息的冗余度，Shannon 提出了混乱与扩散的概念，加密体制中要求充分且均匀的利用密文空间，Hash 函数同样要尽量做到相应明文对应的 Hash 密文不相关。因为结果用二进制表示，每比特只有 1 或 0 两种可能，因此理想的 Hash 的扩散效果应该是初值的细微变化将导致结果的每比特都以 50% 的概率变化。

我们采用的测试方法是：在明文空间中随机地选取一段明文求其 Hash 值，然后改变明文 1比特的值得到另一 Hash 结果，比较两个 Hash 结果求出变化的比特数 Bi。一共进行 N 次类似的测试，可画出相应的比特变化数分布图：图 6 表示N 为 2048 次时相应的比特变化数分布图。

图 6 2048 次 bit 变化数的分布图Fig. 6. The distribution of 2048 bits

从图 6 可以看出，明文 1 比特变化所引起的Hash 值实际变化的比特数非常集中地分布在理想状态的变化数 64 比特附近，表明该算法具备很强的混乱与扩散能力。为了进一步阐明该算法的功能，我们定义以下的四个统计量。

分别经 N＝128, 256, 512, 1024, 2048 次测试，得到本算法的实验数据如表 1 所示。

从表 1 中的数据可以看出，本算法的平均变化比特数和每比特平均变化概率都非常接近理想状态下的 64 比特和 50%，相当充分和均匀地利用了密文空间，从统计效果上保证了攻击者无法在已知一些明文密文对的情况下伪造或反推出其他的明文密文。另外，和很小，表明本算法 Hash 的混乱和扩散性能相当稳定。

4.3 抵抗碰撞和生日攻击性分析

我们将任意改变 1 比特得到的 2048 个 Hash值进行统计分析，其中这 2048 个值都以 16 进制保存。我们统计其在相同位置上对应的字符相等的个数，经仿真，统计结果的分布为：n(0)＝258，n(1)＝553，n(2)＝613，n(3)＝369， n(4)＝174，n(5)＝75，n(6)＝19，n(7)＝7，n(8)＝0，并且超过 8 个字符相等的 Hash 值数目均为0，其具体的字符统计分布图如图 7 所示。

图 7 相同位置有相同字符的 Hash 值统计Fig. 7. The Hash value of the same char in the same location

我们通过以下的实验来定量地测试本算法的抗碰撞能力[13]：在明文空间中随机地选取一段明文求出并以 ASCII 码形式存储其 Hash 值，然后随机地选择并改变明文中 1比特的值得到另一新的 Hash 结果，同样以 ASCII 码形式存储其 Hash值。比较两个 Hash 结果，记录在相同位置上有相同值得 ASCII 码字符的数目，并且利用公式计算两个 Hash 值的绝对差异度。其中，和分别是原始 Hash 和新的 Hash值的第 i 个 ASCII 码字符，而函数 t(*)将 ASCII码字符转化为它们相应的十进制数值。我们在Logistic 映射 μ＝3.7 初始值 x0＝0.5，Chebyshev映射初始值为 x0＝0.2 的参数下，做了 2048 次实验，得到 d 的最大值、最小值、平均值和平均每个字符的差异度列于表 2 中。由表可得，该算法的抗碰撞性能良好。

表 1 混乱与扩散性能实验Table 1. The result of experiment on diffusion and confussion

表 2 两个 Hash 值的绝对差异度Table 2. The absolute difference degree of two Hash values

4.4 与 SHA-3 算法的性能比较

通过上述小节的分析，我们可以看出本算法与 SHA-3 算法类似，均可以满足 Hash 函数的基本特征，同时相对于 SHA-3 算法，该算法主要优点体现在以下两点：第一，本算法引入了混沌映射，具有更好的混乱和扩散特性；第二，目前还没有很好的针对于混沌映射的量子攻击算法，而该算法可以抵抗量子攻击。但由于该算法在参数生成过程中加入了混沌映射，使其与 SHA-3算法的效率相比还有一定差距，因此我们下一步工作的重点就是针对算法的效率问题做进一步的改进。

5 小 结

本文提出了一种基于神经网络的双混沌Hash 函数的构造方法，其中神经网络的参数由Logistic 映射和 Chebyshev 映射结合起来的双混沌系统产生，具有更加广泛的密钥空间，并且混沌特性更好。将初始值通过这种双混沌系统进行迭代产生神经网络的参数，明文以 512 比特分块读入，使用每次产生的 Hash 值去逐步更新神经网络的参数，从而使每次的 Hash 结果都与前面所有的明文和参数相关，这一特点使得本方案的系统具有天生强化雪崩效应的能力，更加确保了最终 Hash 值的每一比特都与消息的所有比特相关，消息或者初始值的微小变化，通过迭代过程不断的扩散放大，最终导致完全不同的 Hash 结果。经过理论分析和实际仿真验证，本方案构造的单向 Hash 算法满足 Hash 算法要求的初值敏感性、不可逆性和弱碰撞性等特点。并且采用分块执行的方案能保证迭代步数与初始文本长度基本是成正比关系，具有较高的效率，具有成为一种快速使用的单向 Hash算法的潜力。

[1] Kou WD. Network Security and Standards [M]. Boston: Kluwer Academic Publishers, 1997.

[2] Pieprzyh J, Sadeghiyan B. Design of Hashing Algorithm [M]. Berlin: Springer-verlag, 1993.

[3] Rivest R. The MD5 Message-Digest Algorithm [Z]. MIT Laboratory for Computer Science and RSA Data Security, Inc.

[4] FIPS PUB 180-1. SHA-1 Standard, Secure Hash Standard [S].

[5] Wang SH, Li D, Zhou H. Collision analysis of a chaos-based hash function with both modification detection and localization capability [J]. Communications in Nonlinear Science and Numerical Simulation, 2012, 17(2): 780-784.

[6] Wang SH, Hu G. Coupled map lattice based hash function with collision resistance in single-iteration computation [J]. Information Sciences, 2012, 195: 266-276.

[7] Wang Y, Liao XF, Xiao D, et al. One-way hash function construction based on 2D coupled map lattices [J]. Information Sciences, 2008, 178(5): 1391-406.

[8] Akhavan A, Samsudin A, Akhshani A. Hash function based on piecewise nonlinear chaotic map [J]. Chaos, Solitons & Fractals, 2009, 42(2): 1046-1053.

[9] Xiao D, Shih FY, Liao XF. A chaos-based hash function with both modification detection and localization capabilities [J]. Communications in Nonlinear Science and Numerical Simulation, 2010, 15(9): 2254-2261.

[10] 韩敏. 混沌时间序列预测理论与方法 [M]. 北京:中国水利水电出版社, 2007.

[11] 张家树, 肖先赐. 用于混沌时间序列自使用预测的一种少参数二阶 Volterra 滤波器 [J]. 物理学报, 2001, 50(7): 1248-1254.

[12] 赵芮, 王庆生, 温会平. 基于二维 Logistic 与Chebyshev 映射 AES 混沌加密算法 [J]. 信息安全, 2008, 24(11): 43-45.

[13] Wong KW. A combined chaotic cryptographic and hashing scheme [J]. Physics Letters A, 2003, 307(5-6): 292-298.

A Dual Chaotic Hash Function Based on Cellular Neural Network

LIU Hui1,2ZHAO Geng1,2BAI Jian1,2

1( School of Telecommunications Engineering, Xidian University, Xi’an 710071, China )2( Beijing Electronic Science and Technology Institute, Beijing 100070, China )

The Hash function with hig h speed and ef fi ciency has been a hotspot of security. In this paper, a new Hash function based on cellular neural network was proposed. The parameters of the cellular neural network were produced by a unique system which combined the Logistic map with the Chebyshev map. The function can handle the plaintext by the block, and the fi nal 128 Hash value is the xor of every block’s Hash value. The experimental data and simulated analysis show that the proposed algorithm can satisfy the requirements of a secure hash function, and it has some good properties such as diffusion, confusion, weak collision and sensitivity to initial conditions. What’s more, the construction of the scheme can be achieved easily.

double chaos system; Hash function; cellular neural network; Logistic map; Chebyshev map

TN 918

A

2013-10-12

国家自然科学基金(NO61170037)。

刘慧，硕士研究生，研究方向为混沌公钥和信息安全；赵耿(通讯作者)，教授，研究方向为混沌密码理论及其应用和计算机信息安全及保密，E-mail：zg@besti.edu.cn；白健，硕士研究生，研究方向为密码学和格理论。