蛋白质折叠计算机模拟研究进展
2014-07-19魏彦杰张慧玲黄庆生
魏彦杰 张慧玲 黄庆生
(中国科学院深圳先进技术研究院高性能计算技术研究中心深圳市高性能数据挖掘重点实验室 深圳 518055)
蛋白质折叠计算机模拟研究进展
魏彦杰 张慧玲 黄庆生
(中国科学院深圳先进技术研究院高性能计算技术研究中心深圳市高性能数据挖掘重点实验室 深圳 518055)
蛋白质折叠过程中的结构变异可能导致“折叠病”,比如老年痴呆症和多聚谷氨酰胺疾病等。因此蛋白质折叠研究对于揭示“折叠病”致病机理、指导药物设计等具有重大意义。文章阐述了蛋白质折叠计算机模拟研究的研究近况,分别介绍了蛋白质侧链研究、蛋白质折叠算法、蛋白质折叠病研究、蛋白质的分子动力学模拟和蛋白质结构预测等几个方面。
蛋白质折叠;并行蒙特卡洛算法;蛋白质结构预测;分子动力学模拟;蛋白质折叠病
1 引 言
蛋白质折叠问题是研究蛋白质如何在短时间内从一级结构(一维多肽链)折叠为天然三维结构,形成具有生命功能的大分子。生物体的遗传信息(DNA)通过 RNA 转录和翻译过程传递给蛋白质,因此蛋白质折叠也被称为第二遗传密码,相关研究可以帮助揭示生命遗传信息的表达和功能传递的奥秘[1]。在从一级结构到天然三维结构的折叠过程中,蛋白质可发生误折或聚集,其结构和功能因此受到破坏,从而引起“折叠病”,比如老年痴呆症、帕金森氏病和多聚谷氨酰胺疾病等[2]。美国 500 多万老年痴呆症患者每年的花费是 1830 亿美元[3],而中国的老年痴呆症患者也有 500~600 万[4]。蛋白质折叠研究对探索“折叠病”的致病机理意义重大,且有助于蛋白质分子药物的设计,故对“折叠病”的预防和治疗也将起到重大的帮助作用[5]。因此我国将蛋白质研究作为基础科学的四个重大科学计划之一列入“国家中长期科学与技术发展规划(2006-2020)”。
研究蛋白质折叠的实验方法有 X 光晶体衍射,NMR 核磁共振等。虽然实验学方法积累了很多数据、贡献巨大[6,7],然而其耗时长、费用高,而且对于较难结晶的膜蛋白,很难得到其三维结构[6-8]。另一方面,作为一个科学发现的独立手段以及实验方法的重要补充,计算科学在蛋白质折叠研究领域也起着越来越大的作用。近十几年蛋白质折叠的计算机研究方法取得了巨大发展,比如 Folding@home 利用世界范围内的计算机实现了蛋白质折叠的分布式计算[9],David Baker 研究组用蛋白质折叠原理得到了全新构象的蛋白质[10]。本文将从侧链对折叠的影响、高效的结构空间搜索算法、折叠病致病机理、蛋白质大体系的分子动力学模拟以及蛋白质结构预测等领域介绍蛋白质折叠的研究进展。
2 蛋白质侧链研究
因为 20 种天然氨基酸的唯一区别是侧链,所以侧链对蛋白质的结构和功能,以及热力学和动力学特性非常重要[1]。蛋白质折叠的侧链研究主要是研究侧链在蛋白质折叠过程中所起的作用。
比较常用的蛋白质侧链的研究方法有以下几种:(1)研究蛋白质折叠中侧链与侧链之间氢键、双硫键的形成[11];(2)通过分割能量力场,研究侧链与侧链之间能量、侧链与主链之间能量以及主链与主链之间的能量变化[12];(3)研究侧链熵变在蛋白质折叠过程中的作用[13];(4)利用已有的数据和贝叶斯统计方法等研究蛋白质侧链的统计规律,建立一个侧链能量力场或者打分函数等[14];(5)基于圆周统计方法研究侧链的热动力学涨落现象[15]。目前这些研究方法在全面化和系统化方面尚有欠缺。其中,基于氢键或者双硫键的方法要求氨基酸侧链必需可以形成氢键或者双硫键;基于能量分割的方法需要对能量力场的计算做出修改;基于熵的方法以及基于统计学(贝叶斯统计等)的方法需要对蛋白质侧链的结构空间离散化处理,从而实现对不同状态的侧链结构进行统计。
蛋白质计算机模型的构建一般基于角度坐标系或笛卡尔坐标系。角度坐标系中对侧链的研究与笛卡尔坐标系有所不同。由于角度具有2π 周期性,在角度坐标系进行蛋白质折叠的计算机模拟时,对角度变量需要特殊处理。常用的方法是将角度或者角度差简单映射到 0~2π,或者 —π~+π[16]。但当利用角度的平均值和方差研究蛋白质的折叠过程时,基于线性统计学的方法会有许多问题,比如会导致一个单峰分布的角度函数变为双峰分布函数。如图 1 所示,黑点和绿点在空间上本属同一个分布,但由于角度范围的选择,黑点和绿点成为两个不同的分布(两个分布的角度平均值约为—160°和+160°)。
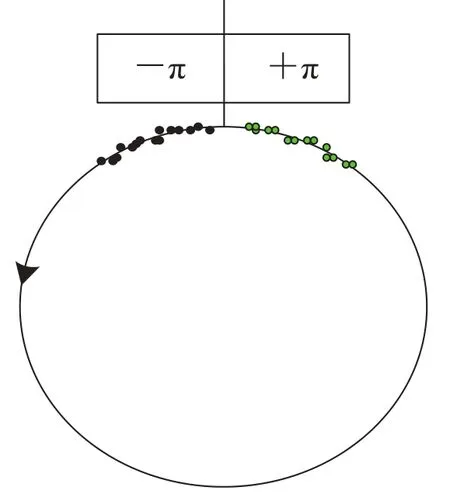
图 1 线性统计导致错误的数据分析Fig. 1. Analysis of circular data using linear statistics
相比于线性统计学,圆周统计学更适用于此类问题。但是圆周统计方差和协方差的数学模型在蛋白质折叠研究中还存在不一致性[15]。圆周统计中角度 a 可以用二维向量表示为角度方差可以用来研究蛋白质折叠过程中物理量的热动力学涨落,其公式为:
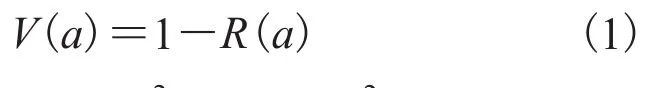
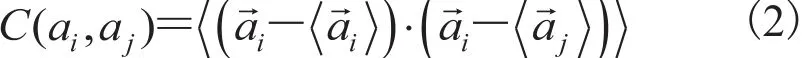

由此导出的方差为:两个方差公式(1)和(3)不一致,因此圆周统计方差和协方差之间在研究蛋白质的两面角时存在不一致性,两方差之间不存在线性统计中的对应关系[15]。文献[15]中研究角度波动在较小的范围内,作者采用了公式(1)计算方差,用如下公式(4)来计算角度协方差:
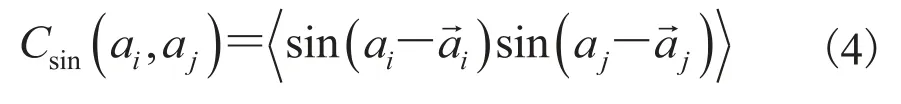
上述计算方差和协方差的方法并不一致,且只在角度波动较小的情况下适用。而波动较大的角度对蛋白质折叠的影响更大,因而具有更大的研究价值。
3 蛋白质折叠空间搜索算法
对于一个只有 100 个氨基酸的蛋白质,其构象数目大约有 10100(假设每个氨基酸只有 10 个构象)。 假设搜索一个构象需要 10—15秒(使用目前最快的千万亿次计算机),则搜索所有的蛋白质结构空间需约 3×1077年。因此搜索所有结构空间不现实,这就对蛋白质结构高效搜索算法提出了更高的要求[17]。蛋白质折叠算法依赖于一个基本假设,即蛋白质的天然结构是蛋白质自由能最低的结构[18]。而传统的分子动力学模拟和蒙特卡洛模拟方法在研究蛋白质折叠时,低温下的模拟都会被“陷”在蛋白质能量的局部最优区间,很难“跳”出来从而找到全局最优解[19]。
广义系综方法(Generalized Ensemble)是解决此问题最常用的一类方法[19]。此方法的核心是使用非波尔兹曼分布函数实现模拟仿真在能量空间的自由行走,从而搜索更为广泛的结构空间,同时还可计算任一温度下的正则系综物理量。这类方法包括多正则系综(Multicanonical)蒙特卡洛方法[20]、Wang-Landau 蒙特卡洛方法[21]、模拟回火(Simulated Tempering)[22]、1/k 搜索[23]和副本交换方法(Replica Exchange Method)[24]等。由于广义系综方法的非波尔兹曼分布函数未知,因此需设计一个繁琐的程序决定此分布函数[19]。并行回火和 Wang-Landau 方法可较为容易地获取非波尔兹曼分布函数。副本交换方法(又称并行回火方法,Parallel Tempering)要求在多个温度下分别进行蒙特卡洛或者分子动力学仿真,经过一定时间后,不同温度下的仿真以一定概率互换结构信息;非波尔兹曼分布函数就是各个温度下的波尔兹曼分布函数的乘积[19]。随着蛋白质系统的增大,此方法需要更多不同温度下的仿真。而选择多少仿真温度,以及如何选取温度成为此算法的一个难点。通过迭代修改一个算法参数 F,Wang-Landau 算法可以自动获得非波尔兹曼分布函数以及系统状态函数,这极大地简化了获取非波尔兹曼分布函数的难度。然而此算法要求预先知道模拟系统的能量范围,这样才能实现模拟仿真在此能量范围内的自由行走[1]。
以上描述的算法大都在分子动力学模拟和蒙特卡洛模拟中实现[19]。比如并行回火蒙特卡洛方法和并行回火分子动力学模拟[25,26]。分子动力学模拟可以研究系统的动力学过程;而蒙特卡洛方法可以研究系统的热动力学过程。高精确度的蛋白质折叠全原子模型模拟需要计算几万到几十万个原子之间的相互作用力,所以分子动力学模拟一般只能模拟纳秒级的折叠过程,因而对于研究发生在微妙到毫秒时间内的蛋白质折叠问题存在局限性。一般分子动力学模拟从一个实验结构开始模拟蛋白质折叠过程[27],而蒙特卡洛方法则可以研究蛋白质折叠的整个热动力学过程,而且蒙特卡洛方法不依赖于初始结构的选择,可以搜索更广泛的结构空间。
其他用于蛋白质折叠的研究算法有:结构空间退火算法(CSA)[28]、遗传算法[29]、 aBB[30]和图论算法[31]等。其中,结构空间退火算法首先搜索大量的可能含最优解的子空间,然后在这些子空间中寻找最优解[28];遗传算法的操作对象是一群蛋白质结构,通过蛋白质结构的突变、结构域选择和重组,实现蛋白质结构的进化,最终找到蛋白质的最优结构[28];aBB 算法在理论上可以确保全局最优解[29]。然而这些算法仅限于寻找蛋白质的最优解,不能研究蛋白质折叠的动力学和热动力学过程。
越来越多的蛋白质折叠研究采用并行算法,比如并行回火算法[25,26]、CSA 和 aBB 混合并行算法[33]、并行遗传算法等[33]。斯坦福大学Folding@home 项目利用世界范围内的计算机实现了蛋白质折叠的分布式计算研究[9]。通过在世界各地的电脑运行一个客户端程序,Folding@ home 将世界上各地的电脑连在一起,构成了世界上最大的超级计算机之一。
蒙特卡洛方法可以研究蛋白质折叠的热动力学性质,而且比分子动力学模拟能搜索更广泛的结构空间。相反,分子动力学模拟更适合研究蛋白质的精细结构变化,比如蛋白质与化学小分子的相互作用。
另外一种研究蛋白质折叠的思路是设计特殊的硬件设备,用于快速计算和模拟蛋白质大分子的热力学和动力学特性。较早的例子是日本的 RIKEN研究机构于 2006年开发的MDGRAPE-3,它主要用于特殊蛋白质结构的分子动力学模拟。MDGRAPE-3 由 4824 个特制的 MDGRAPE-3 芯片以及英特尔 Xeon 处理器构成,对分子的计算通过 MDGRAPE 芯片和通用芯片共同完成。在2006 年时,它已经具备了千万亿浮点运算能力,比当时超算 TOP 500 排名第一的 IBM Blue Gene/L 还要快 3 倍。对两个不同的处于周期边界条件下的生物分子系统的模拟表明,单个 MDGRAPE-3 系统比传统基于 CPU的系统要快 30~40 倍[34]。2009 年 Shaw 发表了面向分子动力学模拟的专用计算机 ANTON[35]。ANTON 包含 512 个节点,每个节点是一个专用计算单元(ASIC),包含一个高通量相互作用子系统和一个可变子系统,前者可以快速计算原子间的两两相互作用,后者则是可编程的子系统,用于完成负荷较轻的其他一些计算。512 个节点之间的总线互联也考虑了分子动力学模拟中空间区域分割的需求。ANTON 特殊的硬件配置给人留下深刻印象,但其实它是软硬件紧密结合的一个平台,设计者重新处理了分子动力学模拟并行化时碰到的负载均衡问题,用了新的办法进行模拟的空间区域分割,甚至专门设计了定点算术运算法则。与 MDGRAPE-3 不同的是,所有的ANTON 计算均在 ASICs 上完成。对于 23,558 原子构成的分子系统的分子动力学模拟,ANTON在一天内可以模拟 17 微秒,而基于通用芯片的系统只能模拟几百纳秒。与 ANTON 相比,ANTON2 在软件和硬件方面做了许多提升,其分子动力学模拟的效率也因此提升了 16%[36]。
4 分子动力学模拟
分子动力学(Molecular Dynamics)模拟是一种数值模拟方法,通过将分子抽象为由化学键连接的质点,按照基于牛顿力学的数学模型(力场)迭代求解分子体系的行为。这种方法比量子力学方法大大节省了计算资源,并且可以求出分子体系随时间演化的行为。在 20 世纪五、六十年代分子动力学模拟被提出来时,它只能应用于简单的单原子分子的同质化体系,解决理论物理学的问题[37,38]。随着它在化学和生物学中的广泛应用,模拟体系的原子数目越来越多、模拟时间越来越长成为自然的需求,而计算机硬件和软件技术的发展以及分子动力学模拟算法本身的优化则提供了这样的可能性。在当代,应用于生物学的模拟体系原子数目通常在 10 万以上,可以是同时包含生物大分子、生物膜、溶剂和无机离子的复杂体系。
巨大的模拟体系要求投入大量的计算资源,为了在可接受的时间内完成模拟,并行计算是现实的选择。NAMD2 是并行化而且可伸缩性很强的分子动力学模拟软件。2013 年 Zhao等[39]在 Blue Waters 超级计算机的支持下,利用 NAMD2 软件进行了包含多达六千万个原子的模拟,协助冷冻电镜解析出了人免疫缺陷病毒-1(Human Immunode fi ciency Virus-1,HIV-1)衣壳的高分辨率结构。HIV-1 是一种逆转录病毒,成熟的病毒表面包被衣壳。衣壳由约 1300 个衣壳蛋白组成。衣壳蛋白相互连接,组成六聚物单元,六聚物单元又相互连接形成六聚物的五聚物(Pentamer-of-Hexamers,POH)或六聚物的六聚物(Hexamer-of-Hexamers,HOH)网格。HOH 网格是规整的长管状,衣壳大体上由 HOH 网格组成,而在特定的 12 个顶点嵌入 POH 网格,在这些顶点处衣壳的表面弯曲闭合。因为衣壳的整体形状不规则,缺乏对称性,用冷冻电镜三维重构技术只能获得分辨率为 8.6Å 的结构。Zhao 等采用了分子动力学柔性拟合(Molecular Dynamics Flexible Fitting,MDFF)技术,将电镜的电子密度图作为外部势,驱动柔性的衣壳蛋白填充电子密度图,得到 HOH 的原子分辨率结构。根据由不同数目 HOH 和 POH 组成的几种网格的形状与衣壳的大体结构比较,初步推出衣壳由 216个 HOH 和 12 个 POH 组成。为了得到完整的衣壳结构,将 MDFF 得到的 HOH 结构和之前报道的 POH 结构组装成成两个模型并进行分子动力学模拟,其中由 216 个 HOH 和 12 个 POH 组成的衣壳的模拟体系共包含 64,332,531 个原子,由186 个 HOH 和 12 个 POH 组成的衣壳的模拟体系共包含 64,423,983 个原子,这些模拟各自持续了 100 ns。通过比较和分析,确认了由 216 个HOH 和 12 个 POH 组成的衣壳的原子分辨率结构。成功模拟如此庞大的生物大分子体系标志着分子动力学模拟软件和并行计算技术的成功结合。
虽然并行计算可以加快大体系的模拟速度,但分子动力学模拟最根本的速度瓶颈在于通用CPU 串行地处理原子间的相互作用。要提升单机(单节点)的计算速度,可以设计专用计算单元,挖掘计算机硬件的潜力。前文提到的面向分子动力学模拟的专用计算机 ANTON 就是最好的例子。ANTON 可以轻松地进行微秒级的分子动力学模拟,速度超越了同时代机器的两个数量级。借助这个机器,Shaw 等[40]用长达 1 ms 的分子动力学模拟探讨了蛋白质折叠的问题;Arkhipov 进行了长达 200 μs 的模拟揭示了 EGF 受体和细胞膜的相互作用[41];Dror 等[42]模拟了小分子配体和 G 蛋白偶联受体自发结合的过程,研究了基于别构效应的药物设计。
除了设计专门的软件和硬件提升模拟速度,改进力场和模拟算法本身也是重要的研究课题。由于力场和模拟算法的改进,计算的速度、精确度和适用的分子体系都有很大进步。常用于模拟生物学体系的 AMBER 力场和 CHARMM 力场都有两类能量项:相邻原子的键长、键角和二面角,和原子两两相互作用的静电力和范德华力。静电力和范德华力是远程相互作用,因此要对体系中所有原子的两两组合求和,这对大体系是非常耗时的步骤。然而,远程相互作用的强度随距离减弱,并且体系中的溶剂有一定的均一性,因此可以利用这些特点设计一些快速算法。Price和 Brooks 提出改进的水溶剂模型 TIP3P,可以配合 Ewald 求和简化水分子中的氢原子的处理[43]。Cerutti 和 Case 设计了多水平 Ewald 求和算法,进一步优化了基于快速傅里叶变换的传统算法[44]。另一方面,一直以来分子动力学模拟方法无法处理共价键的断裂和形成事件,主要是因为这些事件涉及化学变化,因此发生电子转移,不符合分子动力学模拟方法的基本假设。为了模拟更复杂的现象,Walker、Crowley 和 Case 给 Amber 补充了 QM/MM 的功能,兼顾了分子动力学模拟方法的高效率和量子力学方法的灵活性[45]。
总之,分子动力学模拟已经是化学和生物学研究的实用技术,而这项技术也由于应用的驱动快速地发展,能越来越快地处理越来越大和越来越复杂的问题。
5 蛋白质折叠与疾病
蛋白质结构决定了蛋白质的功能,蛋白质功能又与生理密切相关。蛋白质折叠过程中的结构变异可能导致“折叠病”,比如老年痴呆症和多聚谷氨酰胺疾病等。因此对蛋白质折叠和结构的研究有助于研究许多疾病的致病机理,帮助药物设计,从而找到治疗方法。下面以多聚谷氨酰胺(polyQ)疾病为例介绍蛋白质折叠与相关疾病的关系研究。
多聚谷氨酰胺疾病是因三核苷酸 CAG 基因异常重复扩增导致产生多聚谷氨酰胺蛋白的神经系统功能障碍疾病[46]。九种多聚谷氨酰胺疾病的共同特征是患者的大脑细胞中形成了不可溶的蛋白质聚集体。虽然这九种疾病的致病蛋白质以及相应的基因各不相同,但是他们都有共同的多聚谷氨酰胺片段。至今尚未清楚多聚谷氨酰胺蛋白质是如何误叠和聚集,进而导致疾病[47]。可能的致病机理如图 2 表示,与其他许多神经退行性疾病(比如老年痴呆证)相似,多聚谷氨酰胺疾病与多聚谷氨酰胺蛋白的误叠有关[47]。当多聚谷氨酰胺蛋白长度达到 35~40 个氨基酸时,就容易产生这种疾病,而且多聚谷氨酰胺蛋白长度越长疾病就越严重[48]。虽然体内和体外实验也支持蛋白质的误叠导致了疾病的假设,但各个实验的结果仍存在不一致的地方[49]。由于不可溶性,科学家还没得到蛋白质聚集的实验结构[50]。
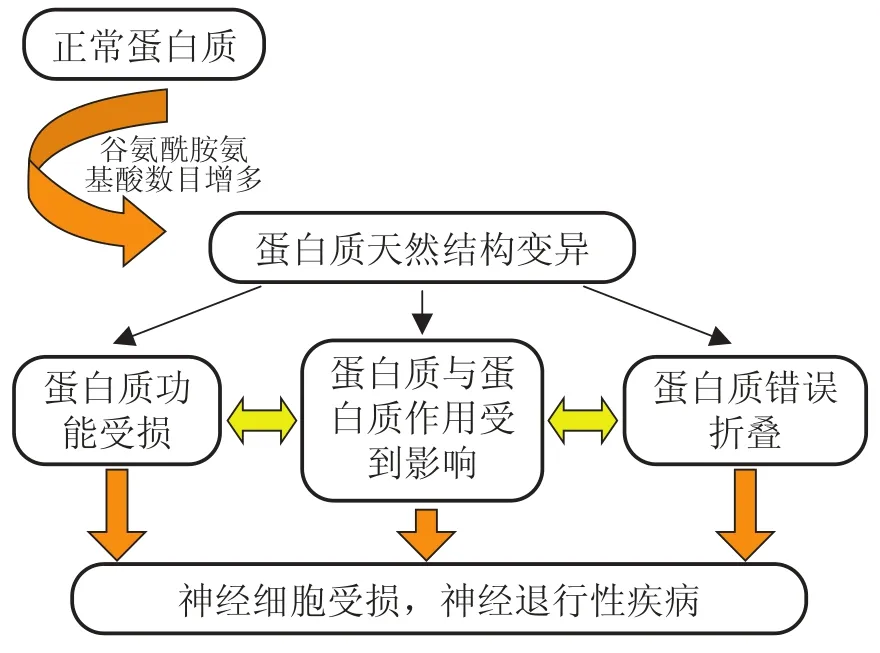
图 2 多聚谷氨酰胺疾病可能致病机理Fig. 2. Possible mechanism of polyQ diseases
用非全原子分子动力学模拟方法[48,51]发现当多聚谷氨酰胺蛋白质长度超过 37 个氨基酸时,多聚谷氨酰胺蛋白质形成 β 螺旋结构;同时Khare1 等[48]指出侧链和主链之间的氢键作用对于 β 螺旋结构的形成起着非常重要的作用,而且β 螺旋结构内部结构紧密,这区别于著名的内部空间疏松的 β 螺旋模型[52];Chopra 等[53]使用蒙特卡洛方法研究发现几个关键的氨基酸决定了多聚谷氨酰胺蛋白质 β 螺旋结构的形成,而且一个稳定的 β 螺旋是蛋白质聚集的基础。
利用并行回火分子动力学方法和非全原子模型,Nelson 等[54]研究了一个被广泛应用的蛋白质系统 CI2-polyQ,发现侧链之间的氢键是蛋白质聚集形成的关键。基于 cross-beta-spine 的空间拉链模体[55,56]建立了长短不同的多聚谷氨酰胺蛋白模型;基于这些模型的分子动力学模拟,Esposito[56]发现短的多聚谷氨酰胺也可以形成蛋白质聚集,而且氢键对蛋白质聚集的稳定性作用巨大。
6 蛋白质结构预测
目前解析蛋白质三维结构的生物学实验方法主要有 X-RAY 和 NMR 法,但这些方法不仅复杂耗时,而且花费较高。由于实验解析法存在这些不足,使得计算方法的发展成为必然。蛋白质三维结构预测的计算方法主要分为三类:同源模建法(Comparative Modeling)[57]、折叠识别法(Threading and Fold Recognition)[58,59]和从头预测法(ab Initio Modeling)[60,61]。同源模建法根据相关蛋白质的序列是否具有较高的相似性,判断它们是否具有相似的三维结构,预测的蛋白质结构具有很高的可信度。折叠识别法将未知蛋白的序列放入结构数据库中,并选择最合适的折叠,以此来预测蛋白质的三维结构,但如果一个预测所需要的蛋白质折叠不存在于折叠文库中,该方法将失效。从头预测法预测程序使用能量最小化原理,搜索每一种可能构象来确定一个具有最低全局能量的构象。
蛋白质结构预测技术评估(C r i t i c a l Assessment of Structure Prediction,CASP)大赛是一个世界性的蛋白质结构预测技术评比活动,被誉为蛋白质结构预测领域的奥林匹克竞赛,自 1994 年开始,每两年组织一届。尽管近年来在 CASP 中,不基于模板的预测方法(Free Modeling)在预测精度方面的提升不大,但由于被解析的蛋白质结构不断增多,基于模板的预测方法(Template Based Modeling)在预测的准确度上取得了较大的进步[62]。大赛还将蛋白质残基作用关系预测(Contact Prediction)作为蛋白质三维结构预测比赛的一部分[63]。与往届 CASP 相比,CASP 10 的“Re fi nement Category”中,Mirjalili等[64]使用了分子动力学的方法对预测的蛋白质结构进行优化,并首次实现了对所有 CASP 10 目标蛋白预测精度的整体提升。
7 总 结
本文从蛋白质折叠中的侧链研究、蛋白质折叠算法研究、蛋白质分子动力学模拟以及蛋白质折叠病研究等方面详细介绍了蛋白质折叠计算机模拟研究的进展,这些进展推动了蛋白质功能的研究和基于蛋白质折叠的药物设计,表明计算机模拟方法在生命科学的研究中扮演着越来越重要的角色。
[1] McKee T, McKee JR. 生物化学导论 [M]. 北京:科学出版社, McGraw-Hill出版社, 2000.
[2] Selkoe DJ. Folding proteins in fatal ways [J]. Nature, 2003, 426: 900-904.
[3] The Alzheimer’s Association. Alzheimer’s Disease Facts and Figures [EB/OL]. http://www.alz.org/ alzheimers_disease_facts_and_ fi gures.asp.
[4] 范东辉. 严重影响健康的老年痴呆症 [J].中国检验检疫, 2006, 12: 64.
[5] Motta A, Reches M, Pappalardo L, et al. The preferred conformation of the tripeptide Ala-Phe-Ala in water is an inverse Gamma-turn: implications for protein folding and drug design [J]. Biochemistry, 2005, 44 (43): 14170-14178.
[6] Wuthrich K. Protein structure determination in solution by NMR spectroscopy [J]. The Journal of Biological Chemistry, 1990, 265(36): 22059-22062. [7] Drenth J. Principles of Protein X-Ray Crystallography [M]. New York: Springer-Verlag Inc., 1990.
[8] White SH. The progress of membrane protein structure determination [J]. Protein Science, 2004, 13: 1948-1949.
[9] Larson SM, Snow CD, Shirts M. Folding@ Home and Genome@ Home: Using distributed computing to tackle previously intractable problems in computational biology [J]. Proceedings of the Computational Genomics, 2002.
[10] Kuhlman B, Dantas G, Ireton GC, et al. Design of a novel globular protein fold with atomic-level accuracy [J]. Science, 2003, 302 (5649): 1364-1368.
[11] Shao QA, Gao YQ. Temperature dependence of hydrogen-bond stability in beta-hairpin structures [J]. Journal of Chemical Theory and Computation, 2010, 6(12): 3750-3760.
[12] Spassov VZ, Yan L, Flook PK. The dominant role of side-chain backbone interactions in structural realization of amino acid code. ChiRotor: a sidechain prediction algorithm based on side-chain backbone interactions [J]. Protein Science, 2007, 16(3): 494-506.
[13] Doig AJ, Sternberg MJ. Side-chain conformational entropy in protein folding [J]. Protein Science, 1995, 4: 2247-2251.
[14] Dunbrack RL, Cohen FE. Bayesian statistical analysis of protein side-chain rotamer preferences [J]. Protein Science, 1997, 6(8): 1661-1681.
[15] Wei Y, Nadler W, Hansmann UHE. Backbone and sidechain ordering in a small protein [J]. The Journal of Chemical Physics, 2008, 128: 025105.
[16] Hansmann UHE. Parallel tempering algorithm for conformational studies of biological molecules [J]. Chemical Physics Letters, 1997, 281: 140-150.
[17] Subramani A, DiMaggio PA, Floudas CA. Selecting high quality protein structures from diverse conformational ensembles [J]. Biophysical Journal, 2009, 97: 1728-1736.
[18] Anfinsen C. The formation and stabilization of protein structure [J]. Biochemical Journal, 1972, 128(4): 737-749.
[19] Mitsutake A, Sugita Y, Okamoto Y. Generalizedensemble algorithms for molecular simulations of biopolymers [J]. Biopolymers, 2001, 60: 96-123.
[20] Hansmann UHE, Berg BA, Neuhaus T. Recent results of multimagnetical simulations of the ising model [J]. International Journal of Modern Physics C, 1992, 3: 1155-1161.
[21] Wang FG, Landau DP. Efficient, multiple-range random walk algorithm to calculate the density of states [J]. Physical Review Letters, 2001, 86 (10): 2050-2053
[22] Marinari E, Parisi G. Simulated tempering: a new monte carlo scheme [J]. Europhysics Letters, 1992, 19: 451-458.
[23] Hesselbo B, Stinchcombe RB. Monte carlo simulation and global optimization without parameters [J]. Physical Review Letters, 1995, 74: 2151-2155.
[24] Hukushima K, Nemoto K. Exchange monte carlo method and application to spin glass simulations [J]. Journal of the Physical Society of Japan, 1996, 65: 1604-1608.
[25] Hansmann UHE. Parallel tempering algorithm for conformational studies of biological molecules [J]. Chemical Physics Letters, 1997, 281: 140-150.
[26] Sugita Y, Okamoto Y. Replica-exchange molecular dynamics method for protein folding [J]. Chemical Physics Letters, 1999, 314: 141-151.
[27] Hansmann UHE, Okamoto Y. New monte carlo algorithms for protein folding [J]. Current Opinion in Structural Biology, 1999, 9: 177-183.
[28] Lee J, Scheraga HA, Rackovsky S. New optimization method for conformational energy calculations on polypeptides: conformational space annealing [J]. Journal of Computational Chemistry, 1997, 18: 1222-1232.
[39] Pedersen JT, Moult J. Genetic algorithms for protein structure prediction [J]. Current Opinion in Structural Biology, l996, 6: 227-231.
[30] Androulakis IP, Maranas CD, Floudas CA. Prediction of oligopeptide conformations via deterministic global optimization [J]. Journal of Global Optimization, 1997, 11: 1-34.
[31] Samudrala R, Moult J. A graph-theoretic algorithm for comparative modeling of protein structure [J]. Journal of Molecular Biology, 1998, 279: 287-302. [32] Subramani A, Wei Y, Floudas CA. ASTRO-FOLD 2.0: an enhanced framework for protein structure prediction [J]. AIChE Journal, 2012, 58(5): 1619-1637.
[33] Carpio CAD. A parallel genetic algorithm for polypeptide three dimensional structure prediction. A transputer implementation [J]. Journal of Chemical Information and Computer Sciences, 1996, 36: 258-269.
[34] Kikugawa G, Apostolov R, Kamiya N, et al. Application of MDGRAPE-3, a special purpose board for molecular dynamics simulations, to periodic biomolecular systems [J]. Journal of Computational Chemistry, 2009, 30(1): 110-118.
[35] Shaw DE, Dror RO, Salmon JK, et al. Millisecondscale molecular dynamics simulations on Anton [C] // Proceedings of the Conference on High Performance Computing Networking, Storage and Analysis, 2009: 1-11.
[36] Grossman JP, Kuskin JS, Bank JA, et al. Hardware support for fine-grained event-driven computation in Anton 2 [C] // Proceedings of the Eighteenth International Conference on Architectural Supportfor Programming Languages and Operating Systems, 2013: 549-560.
[37] Alder BJ, Wainwright TE. Studies in molecular dynamics. I. general method [J]. The Journal of Chemical Physics, 1959, 31(2): 459-466.
[38] Rahman A. Correlations in the motion of atoms in liquid argon [J]. Physical Review, 1964, 136(2A): A405-A411.
[39] Zhao G, Perilla JR, Yufenyuy EL, et al. Mature HIV-1 capsid structure by cryo-electron microscopy and all-atom molecular dynamics [J]. Nature, 2013, 497(7451): 643-646.
[40] Shaw DE, Maragakis P, Lindorff-Larsen K, et al. Atomic-level characterization of the structural dynamics of proteins [J]. Science, 2010, 330(6002): 341-346.
[41] Arkhipov A, Shan Y, Das R, et al. Architecture and membrane interactions of the EGF receptor [J]. Cell, 2013, 152(3): 557-569.
[42] Dror RO, Green HF, Valant C, et al. Structural basis for modulation of a G-protein-coupled receptor by allosteric drugs [J]. Nature, 2013, 503(7475): 295-299.
[43] Price DJ, Brooks CL. A modified TIP3P water potential for simulation with Ewald summation [J]. The Journal of Chemical Physics, 2004, 121(20): 10096-10103.
[44] Cerutti DS, Case DA. Multi-level ewald: a hybrid multigrid/fast fourier transform approach to the electrostatic particle-mesh problem [J]. Journal of Chemical Theory and Computation, 2009, 6(2): 443-458.
[45] Walker RC, Crowley MF, Case DA. The implementation of a fast and accurate QM/MM potential method in Amber [J]. Journal of Computational Chemistry, 2008, 29(7): 1019-1031.
[46] 周亚芳, 江泓, 汤建光, 等. 蛋白质磷酸化修饰在多聚谷氨酰胺疾病中的研究进展 [J]. 中华医学遗传学杂志, 2008, 25(4): 414-417.
[47] Paulson HL, Bonini NM, Roth KA. Polyglutamine disease and neuronal cell death [J]. PNAS, 2000, 97: 12957-12958.
[48] Khare1 SD, Ding F, Gwanmesia KN, et al. Molecular origin of polyglutamine aggregation in neurodegenerative disease [J]. PLoS Computational Biology, 2005, 1(3): e30.
[49] Wanker EE. Protein aggregation and pathogenesis of huntington’s disease: mechanisms and correlstions [J]. The Journal of Biological Chemistry, 2000, 381: 937-942.
[50] Ogawa H, Nakano M, Watanabe H, et al. Molecular dynamics simulation study on the structural stabilities of polyglutamine peptides [J]. Computational Biology and Chemistry, 2008, 32(2): 102-110.
[51] Merlino A, Esposito L, Vitagliano L. Polyglutamine repeats and beta-Helix structure: molecular dynamics study [J]. Proteins: Structure, Function, and Bioinformatics, 2006, 63: 918-927.
[52] Perutz MF, Finch JT, Berriman J, et al. Amyloid fibers are water-filled nanotubes [J]. Proceedings of the National Academy of Sciences of the United States of America, 2002, 99(8): 5591-5595.
[53] Chopra M, Reddy AS, Abbott NL, et al. Folding of polyglutamine chains [J]. The Journal of Chemical Physics, 2008, 129: 135102.
[54] Barton S, Jacak R, Khare SD, et al. The length dependence of the polyQ-mediated protein aggregation [J]. The Journal of Biological Chemistry, 2007, 282(35): 25487-25492.
[55] Nelson R, Sawaya MR, Balbirnie M, et al. Structure of the cross-beta spine of amyloid-like fi brils [J]. Nature, 2005, 435: 773-778.
[56] Esposito L, Paladino A, Pedone C, et al. Insights into structure, stability, and toxicity of monomeric and aggregated polyglutamine models from molecular dynamics simulations [J]. Biophysical Journal, 2008, 94(10): 4031-4040.
[57] Marti-Renom MA, Stuart AC, Fiser A, et al. Comparative protein structure modeling of genes and genomes [J]. Annual Review of Biophysics and Biomolecular Structure, 2000, 29: 291-325.
[58] Bowie JU, Luthy R, Eisenberg D. A method to identify protein sequences that fold into a known three-dimensional structure [J]. Science, 1991, 253: 164-170.
[59] Jones DT, Taylor WR, Thornton JM. A new approach to protein fold recognition [J]. Nature, 1992, 358: 86-89.
[60] Wu S, Skolnick J, Zhang Y. Ab initio modeling of small proteins by iterative TASSER simulations [J]. BMC Biology, 2007, 5: 17.
[61] Das R, Baker D. Macromolecular modeling with rosetta [J]. Annual Review of Biochemistry, 2008, 77(1): 363-382.
[62] Kryshtafovych A, Fidelis K, Moult J. CASP10 results compared to those of previous CASP experiments [J]. Proteins, 2014, 82(Suppl 2): 164-174.
[63] Moult J, Fidelis K, Kryshtafovych A, et al. Critical assessment of methods of protein structure prediction (CASP)-round x [J]. Proteins, 2014, 82(Suppl 2): 1-6.
[64] Mirjalili V, Noyes K, Feig M. Physics based protein structure refinement through multiple molecular dynamics trajectories and structure averaging [J]. Proteins, 2014, 82(Suppl 2): 196-207.
Advances on Computer Simulations of Protein Folding
WEI Yanjie ZHANG Huiling HUANG Qingsheng
( Shenzhen Key Lab for High Performance Data Mining, Center for High Performance Computing, Shenzhen Institutes of Advanced Technology,Chinese Academy of Sciences,Shenzhen 518055,China )
Protein misfolding leads to many diseases, such as Alzhemizer disease and polyQ diseases, etc. Protein folding is vital for the mechanism study of folding-related diseases. In this paper, several aspects in protein folding were reviewed, including the side chain ordering, computational algorithms for protein folding, folding diseases, molecular dynamics simulation and structure prediction.
protein folding; parallel monte carlo method; protein structure prediction; molecular dynamics simulation; protein folding disease
TG 156
A
2013-11-29
国家自然科学基金项目(11204342);深圳市科创委项(JCYJ20120615140912201);深圳市孔雀计划项目(KQCX20130628112914299)。
魏彦杰(通讯作者),博士,研究方向为计算生物学,E-mail:yj.wei@siat.ac.cn;张慧玲,硕士,研究方向为生物信息学和计算生物学;黄庆生,博士,研究方向为生物信息学和计算生物学。
