基于人工蜂群算法的胶囊内窥镜位姿磁定位研究

郑子昭何小其胡 超

1(太原科技大学 太原 030024)

2(浙江大学宁波理工学院 宁波 315100)

基于人工蜂群算法的胶囊内窥镜位姿磁定位研究

郑子昭1何小其2胡 超2

1(太原科技大学 太原 030024)

2(浙江大学宁波理工学院 宁波 315100)

胶囊内窥镜技术是胃肠道内窥镜检查的一个重大突破，但其临床反馈尚有一些问题待解决，其中一个问题就是定位跟踪。在各种可能的定位技术中，磁体定位技术具有不用供电且体积小等特点，应用于胶囊内窥镜的定位问题是非常合适的。文章针对磁体定位技术中的磁偶极子定位模型，提出一种新的算法——混合人工蜂群算法，并将该算法与标准人工蜂群算法、随机复合形算法、Levenberg-Marquart(LM)算法进行对比。实验结果表明，混合人工蜂群算法在算法定位精度、算法稳定性和抗噪能力等方面，比其他三种算法具有更优越的性能。

胶囊内窥镜；磁定位技术；优化技术；人工蜂群算法

1 引 言

由于磁铁无需电源便可产生静磁场信号，且很容易地建立一个微型无线定位系统，这使得磁定位技术引起许多学者关注[1-8]。磁定位技术在对近距离目标的跟踪方面有很多的应用，尤其适用于人体。例如 Golden 等[2]发明了一种可以在病人体内定位的医疗管。该医疗管主要通过检测仪器感应与医疗管相连接的磁铁所产生的磁场强度来定位，但其尚未能监测出磁铁的方向，也未能实时跟踪目标的轨迹。Prakash 等[3]提出了一种将单目标磁偶极子模型定位技术应用在人体外的磁性标记方法。此方法采用八磁通门磁力传感器测量磁性标记物的磁场，之后通过定位算法来计算它的位置和方向。

国内方面，侯文生等[4]设计了一种微型诊疗装置的定位系统，该系统首先通过霍尔传感器阵列对包含在微型装置中的永磁体周围的空间磁场进行检测，然后由多路信号处理电路对检测到的信息进行采集，最后通过串口通信电路传输给后台主控计算机对数据进行分析处理，而后就可以计算出诊疗装置在体内的空间位置等信息，并显示出来。王坤东等[5]将两个三轴传感器封装在胶囊内，由胶囊和永磁体的空间位置关系模型，建立了与传感器输出和胶囊位置变量相关的一组多元非线性方程。但该方法建立的磁场模型较复杂，求解算法的快速性、全局最优性等方面还存在缺陷。胡超等[6,7]提出了一种利用三轴磁传感器阵列跟踪定位内嵌磁体的胶囊内窥镜定位算法。该算法利用目标矩阵的最小特征值对应的特征向量获得定位参数初值，并以此作为基础提高定位精度。其实验结果表明，这种算法比以往仅仅使用线性算法具有更好的精确性，并且能克服非线性算法可能无法提供正确的全局最优解这个问题，算法的时间效率得到较好的改善。

随着科学技术的不断发展，胶囊内窥镜检测方法逐渐成为胃肠道疾病尤其是小肠疾病诊断的首选方法。然而，在人体胃肠道中胶囊的运动依靠肠胃的蠕动，如果医生需对特定区域进行观察，获取胶囊准确的定位信息是至关重要的。本文针对基于磁偶极子的定位模型[8]，提出一种新的算法——混合人工蜂群算法，并从算法的定位精度、算法稳定性和抗噪能力三方面与标准人工蜂群算法、随机复合形算法和 Levenberg-Marquart(LM)算法进行对比，旨在探索一种性能更优越的准确定位胶囊信息的算法，为相关科研和医疗应用提供科学理论依据。

2 胶囊内窥镜磁定位模型

胶囊内窥镜磁场定位技术是在原有胶囊内窥镜的基础上增加一个圆环型薄磁套[9]，如图1 所示。通过利用人体外部布置磁传感器阵列(见图2)，来获取胶囊在人体内运动时，在不同位置所产生的磁场的磁场强度数值。由于传感器阵列接收的磁场信号与胶囊内磁体相对传感器的位置和方向有关，通过对这些传感器接收的信息进行处理和采样后，利用相应算法可计算出胶囊的位置和方向参数。

图1 磁套胶囊内镜Fig.1. Wireless capsule endoscope

由于胶囊在人体胃肠道内运动的过程中，胶囊的位置和方向一直在改变，因此，我们定义一个固定的坐标系(如图3 所示)来建立胶囊磁定位的模型。

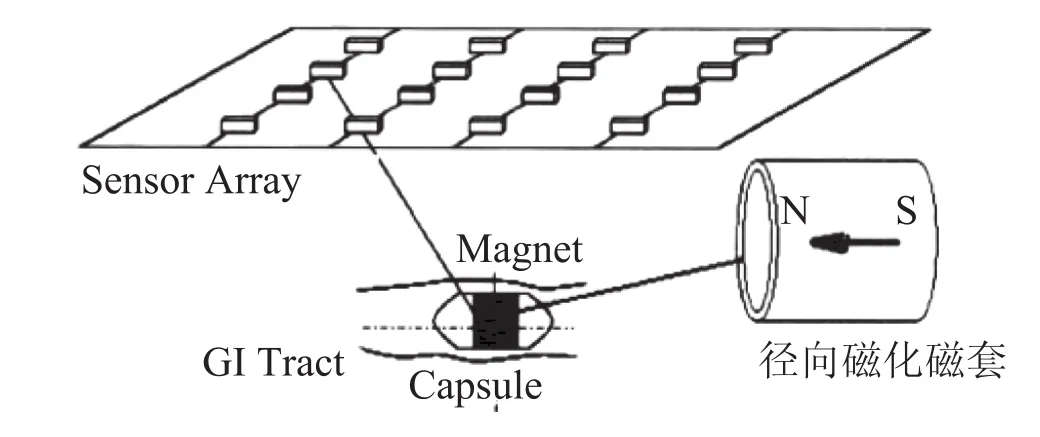
图2 轴向磁化的胶囊内镜的定位Fig.2. Localization of axially magnetized capsule endoscope

图3 磁定位的坐标系Fig.3. Coordinate system for magnetic localization

在该坐标系中，磁体中心坐标用(a, b, c)T表示；在位置(xl, yl, zl)T上放置三维磁传感器(序号为 l，l＝1, 2, …, N)，定义坐标轴 x、y、z 的单位坐标向量分别为 i、j、k ，则磁场强度即为：

其中，Blx、Bly和 Blz为 Bl在(xl, yl, zl)T位置上的3 个分量；N 为总传感器数量；μr为相对导磁率(空气中 μr≈1)；μ0为真空导磁率(μ0＝4π×10—7T·m／A)；MT为表征磁体磁场强度的常数(与体积和磁化强度相关)；Pl＝(xl—a, yl—b, zl—c)T为第 l 个传感器位置相对磁体中心位置的矢量；Rl为 Pl的模，即H0＝(m, n, p) 为表征磁体磁场方向的三维矢T量，所以加上约束

将式(1)展开，有

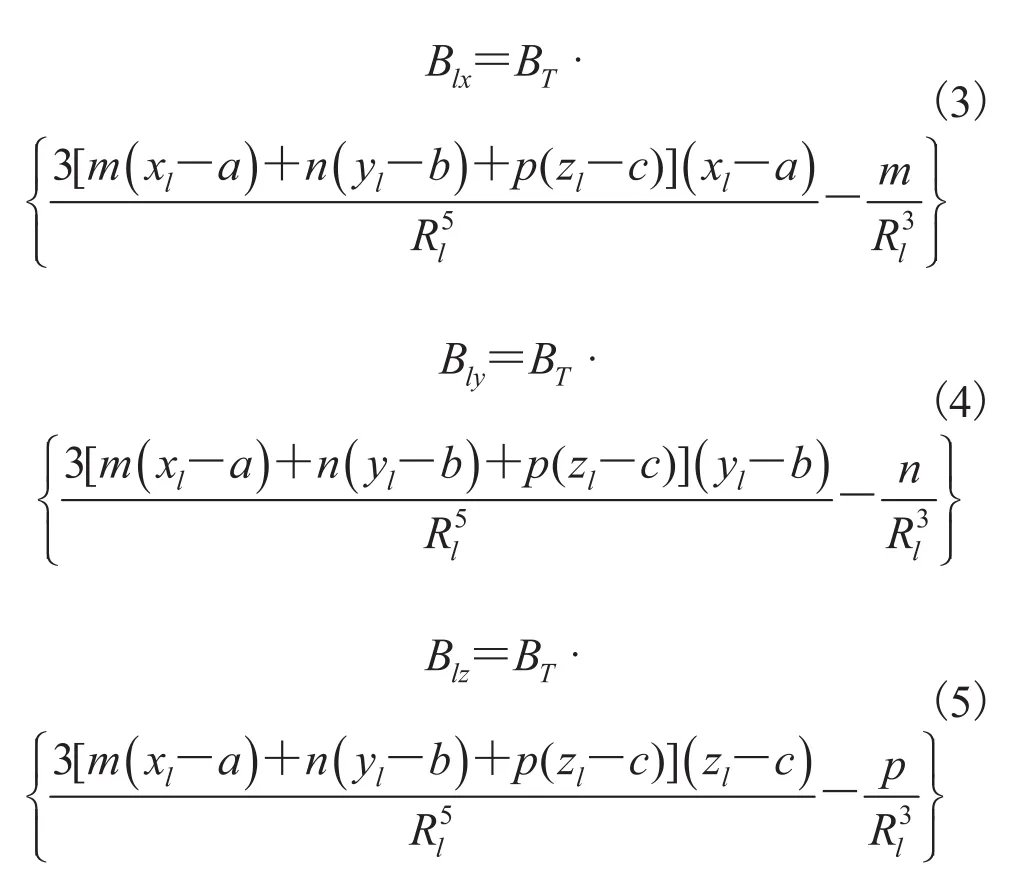
现在，需要用式(2)～(5)解出(a, b, c)T和(m, n, p)T。根据胶囊内窥镜磁定位的模型，有 5 个未知参数需要求解，需要传感器数目应 N5。我们定义一个目标误差函数如下：

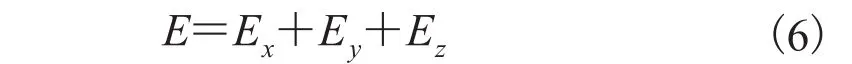
其中，

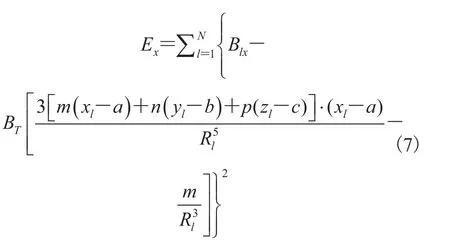
这是一个非线性最小二乘求解问题，则胶囊内窥镜的定位问题转化为非线性优化问题。我们通过优化算法寻找(a, b, c)T和(m, n, p)T使目标误差最小，即

为了衡量算法的有效性，定义定位和定向误差：

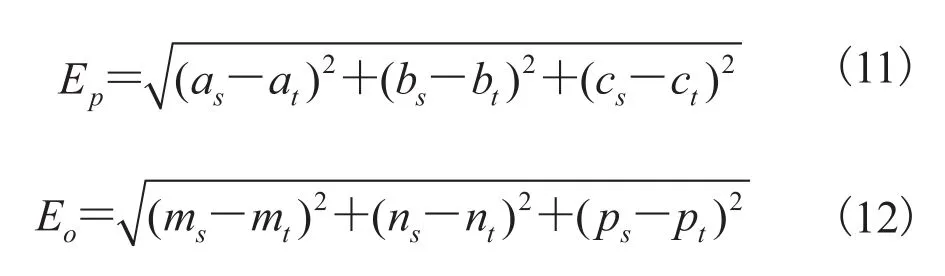
其中，(at, bt, ct, mt, nt, pt)和(as, bs, cs, ms, ns, ps)表示设定和计算的位置和方向参数。

3 改进的人工蜂群算法

3.1 人工蜂群算法

人工蜂群(Artificial Bee Colony，ABC)算法由 Karaboga 于 2005 年提出[10]，并且其性能在2007 年被测试分析[11]。人工蜂群算法通过模仿真实蜜蜂寻找蜜源并且和附近蜜蜂分享蜜源信息的行为发展而来。在算法中，人工蜜蜂种群被定义和分成三类：引领蜂、跟随蜂和侦察蜂。在寻找蜜源的过程中它们每个个体都扮演着不同的角色：每个蜜源吸引一只引领蜂，引领蜂将蜜源信息与跟随蜂共享，蜜源适应度越高招来的跟随蜂越多；跟随蜂到达蜜源后对该蜜源做一次邻域搜索，找到新蜜源，作比较，记录开采次数；而侦察蜂在解空间随机产生一个新的蜜源代替原来的蜜源。人工蜂群算法的过程的描述如下：

随机产生 2N 个位置，取较优异的 N 个作为蜜源位置，引领蜂发现蜜源并记忆，在各蜜源附近按式(13)搜索新蜜源：

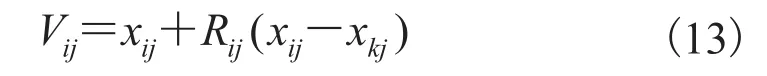
其中，Vij为新的蜜源位置；xij为蜜源的第 j 维位置；xkj为随机选择的不等于 i 的蜜源的第 j 维位置；Rij为[—1, 1]间的随机数。

根据前后蜜源的花蜜数量(适应度值)选择较优蜜源并作为初始标记蜜源；引领蜂释放与标记蜜源质量成正比的信息，用来招募跟随蜂，跟随蜂利用轮盘赌方式

取合适的标记蜜源并在其附近按式(13)搜索新蜜源，并与初始标记蜜源进行比较，选取较优异的蜜源更改本次循环的初始标记蜜源。但如果在采蜜过程中，蜜源经若干次搜索不变，相应的引领蜂变成侦查蜂，随机搜索新蜜源代替初始标记蜜源中的相应位置，确定最终蜜源。

按照上述方式反复循环迭代，直到达到算法的终止条件。

3.2 模式搜索法

模式搜索法[12]主要由移动过程组成：探测移动和模式移动。其中，探测移动是沿坐标轴方向的移动，模式移动则是沿相邻两个探测点连线方向上的移动。两种移动模式交替进行，目的是顺着函数值下降的最佳方向直到找到结果。模式搜索算法步骤如下：

(1)给定初始点 x0，初始步长 δ＝(δ1, δ2, …, δn)T＞0，加速系数 γ＞0，收缩系数 θ∈(0, 1)及精度 ε＞0，置 k＝0；

(2)令 y＝xk；

(3)从 y 出发，依次做平行于单位矢量 ej(j＝1, 2, …, n)的轴向探测移动；

3.3 改进的人工蜂群算法

人工蜂群算法是一种蜂群觅食行为为基础的群智能搜索算法，在优化技术领域具有竞争力。然而，Zhu 等[13]指出人工蜂群算法在全局搜索和局部搜索中并不平衡，局部搜索能力略显不足，在进化后期位置相似度高、更新速度慢的缺点致使对算法局部搜索能力的提高是必要的。模式搜索法是一种经典的局部搜索算法，其优点是算法实现过程中并没有使用目标函数的导数。

本文将人工蜂群算法与模式搜索方法相结合，提出了一种新的人工蜂群算法——混合人工蜂群算法(Hybrid Artificial Bee Colony，HABC)，具体步骤如下：

(1)设置主要初始参数：种群数、最大循环次数 Gmax、参数维数和阈值等，其中引领蜂和跟随蜂各占 50%，侦察蜂 1 只；

(2)随机产生 m 个初始解；

(3)引领蜂搜索蜜源，并计算蜜源适应度值，进入循环；

(4)跟随蜂分享蜜源信息，由式(14)选择其中一个蜜源，然后按式(13)搜索邻近新蜜源；

(5)对新蜜源计算适应度值，并根据贪婪机制选择更优的蜜源；

(6)当最大循环次数 Gmax 整除 2*D(D 是参数维数)时，在所有的蜜源中随机选择 1 个进行模式搜索找到更优的蜜源；

(7)若循环经限定次数后，蜜源适应度值仍不达标则放弃，引领蜂变成侦察蜂继续搜索，由式(15)更新位置；

(8)存储此时的最优解；

(9)循环次数加 1；

(10)满足终止条件，达到最大循环次数。

4 实验与分析

本文分别从定位精度、算法稳定性和算法抗噪声能力三方面，利用位置误差和方向误差两个指标，对标准人工蜂群算法(Artificial Bee Colony，ABC)、混合人工蜂群算法、随机复合形算法(Random Complex Algorithm，RCA)和Levenberg-Marquart(LM)算法开展了比较实验。为有效地评价四种算法的性能，构建了基于 16个三维磁传感器布局的仿真，传感器位置布局如图4 所示，16 个传感器均匀布置在 240 mm×240 mm范围的 x-y 平面。

4.1 算法定位精度

算法精度是衡量算法性能的首要因素，针对磁偶极子的定位模型，在初始设定位置误差 dl＝10 cm 时，利用 32 个测试向量，对标准人工蜂群算法(ABC)、混合人工蜂群算法(HABC)、随机复合形算法(RCA)和 Levenberg-Marquart(LM)算法的定位精度进行测试，测试结果如图5 和 6所示。

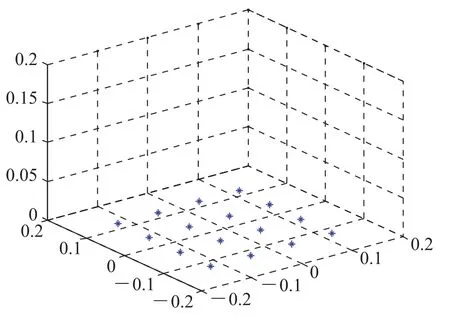
图4 传感器的布置Fig.4. Placement of sensors

由图5 可知，标准人工蜂群算法的位置误差最小，结果为 0 mm；混合人工蜂群算法的位置误差数量级达到 10—12mm，平均值为 0.19×10—12mm；随机复合形算法平均值为 0.70×10—2mm；LM 算法数量级达到 10—8mm，平均值为 0.25×10—8mm。从位置误差的角度分析，混合人工蜂群算法和标准人工蜂群算法具有相近的性能，且优于随机复合形算法和 LM 算法。由图6 可知，四种算法的方向误差相差较大，标准人工蜂群算法方向误差的平均值为 0.13×10—4，随机复合形算法方向误差的平均值为 0.63×10—4，LM 算法方向误差的平均值误差为 0.38×10—4，混合人工蜂群算法方向误差的平均值为 0.46×10—14，明显优于其他三种算法。综合位置和方向两方面的误差精度可知，混合人工蜂群算法获得了优于其他三种算法的性能。

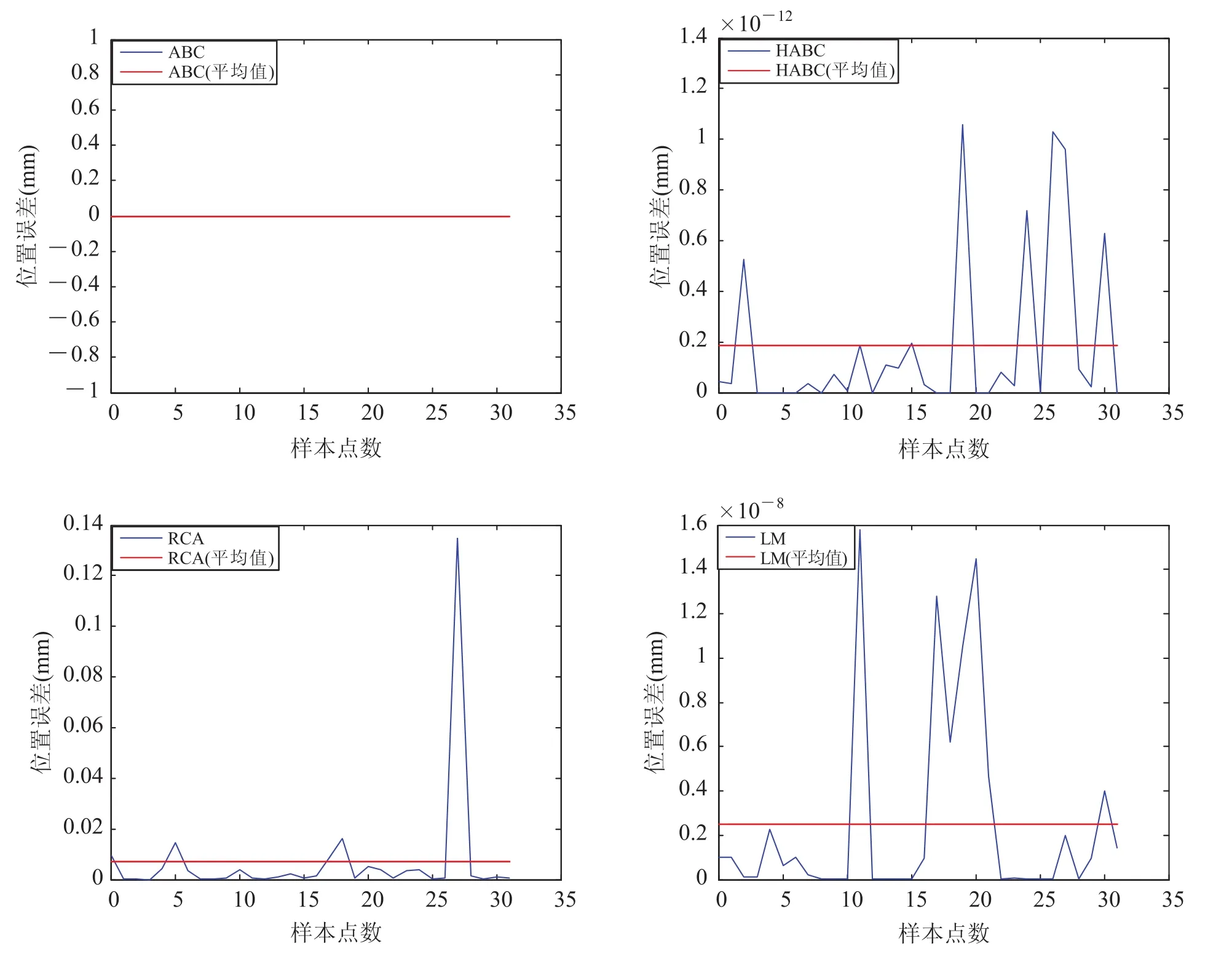
图5 四种算法位置误差Fig.5. Location errors of four algorithms

图6 四种算法的方向误差Fig.6. Orientation errors of four algorithms

4.2 算法的稳定性

针对所有 32 个测试向量，初始设定位置的误差从 10 cm 到 100 cm 过程中，标准人工蜂群算法、混合人工蜂群算法、随机复合形算法和LM 算法有效测试向量(测试向量得到的结果定位误差在 5 mm 以内，方向误差小于 5%)所占比例的仿真结果如图7 所示。

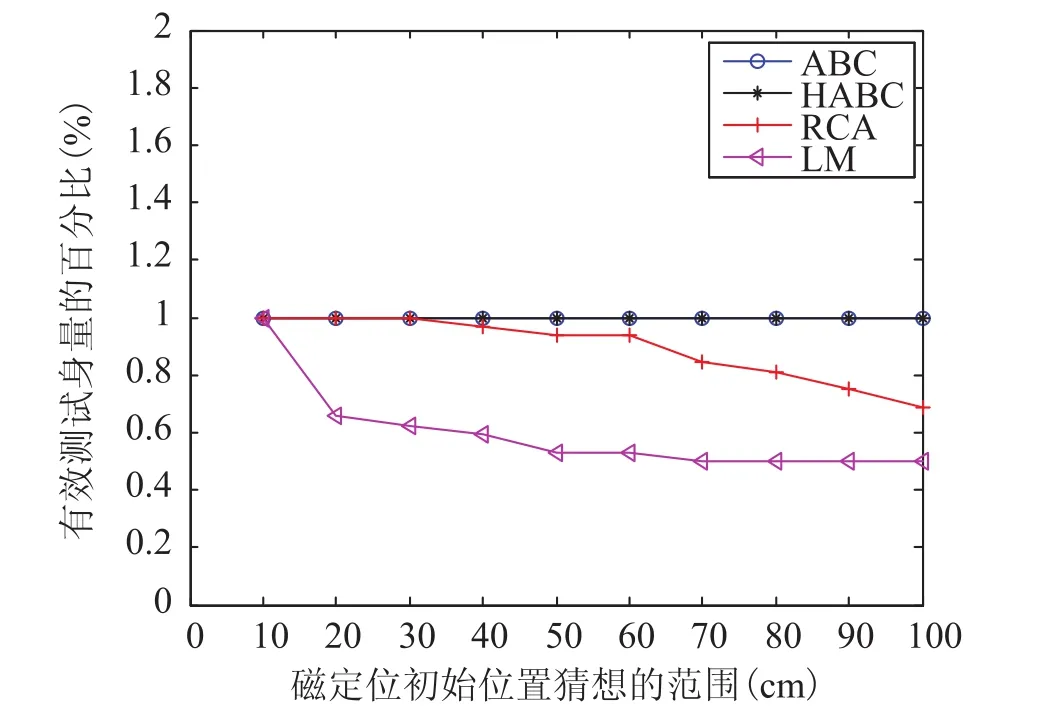
图7 不同初始设定位置误差时的有效测试向量比例Fig.7. Ratio of effective test vector under different error levelof the initial guess of magnet location

仿真结果证明，在不断扩大初始设定位置误差的过程中，随机复合形法和 LM 算法有效测试向量的比例都会下降，但标准人工蜂群算法和混合人工蜂群算法有效测试向量的比例保持稳定，可见标准人工蜂群算法和混合人工蜂群算法的稳定性较好。

4.3 抗噪能力

为了测试四种算法的抗噪能力，针对测试向量 Vr＝[—0.088 0.000 0.097 0.1124 0.9937 0]，初始设定位置的误差为 10 cm。当噪声等级 dl 从0.1 加到 50 时，分别对标准人工蜂群算法、混合人工蜂群算法、随机复合形算法和 LM 算法的位置误差、方向误差的变化情况进行了仿真测试，结果如图8 所示。

图8 噪声等级 从 0.1 到 50 时的位置和方向误差Fig.8. Localization and orientation error sensors via noise level (0.1-50)

由图8 可知，当噪声等级 dl 从 0.1 加到50 时，混合人工蜂群算法定位误差的平均值为0.19 mm，最大值为 0.99 mm；方向误差的平均值为 0.23%，最大值为 0.88%；标准人工蜂群算法定位误差的平均值为 0.21 mm，最大值为0.67 mm；方向误差的平均值为 0.35%，最大值为 1.44%；随机复合形算法定位误差的平均值为0.25 mm，最大值为 1.24 mm；方向误差的平均值为 0.45%，最大值为 1.77%。LM 算法定位误差的平均值为 0.55 mm，最大值为 1.99 mm；方向误差的平均值为 1.01%，最大值为 4.54%。可见，在抗噪声能力上，混合人工蜂群算法要略优于标准人工蜂群算法，而明显优于随机复合形算法和 LM 算法。

5 总 结

对于嵌有永磁铁的胶囊内窥镜的位置和方向的定位问题，我们提出一种新的定位算法——混合人工蜂群算法。混合人工蜂群算法是在人工蜂群算法的基础上以模式搜索法对其进行局部搜索加强算法的搜索性能的一种算法。仿真结果表明，混合人工蜂群算法在定位精度要优于人工蜂群算法，而且在抗噪声能力方面混合人工蜂群算法也有改善，同时，也发现群智能算法(HABC和 ABC)在胶囊内窥镜定位中，在定位精度、稳定性和抗噪声等方面都优于局部搜索算法(LM 和RCA)。但是，标准人工蜂群算法和混合人工蜂群算法的运行时间比局部搜索算法更长，今后需要作进一步的改进。

[1] Schlageter V, Besse PA, Popovic RS, et al. Tracking system with five degrees of freedom using a 2D-array of Hall sensors and a permanent magnet [J]. Sensors and Actuators A: Physical, 2001, 92(1):37-42.

[2] Golden RN, Silverstein FE. Apparatus and method for locating a medical tube in the body of a patient: US, Patent 5,622,169 [P]. 1997-4-22.

[3] Prakash NM, Spelman FA. Localization of a magnetic marker for GI motility studies: an in vitro feasibility study [C] // Proceedings of the 19th Annual International Conference of the IEEE Engineering in Medicine and Biology Society, 1997, 6: 2394-2397.

[4] 侯文生, 郑小林, 彭承琳, 等. 体内微型诊疗装置磁定位简化模型的实验研究 [J]. 仪器仪表学报, 2006, 26(9): 895-897.

[5] 王坤东, 颜国正, 姜萍萍, 等. 基于永磁磁场的电子胶囊定位系统 [J]. 生物医学工程学杂志, 2007, 24(5): 1148-1151.

[6] Hu C, Meng M, Liu PX, et al. Image distortion correction for wireless capsule endoscope [C] // 2004 IEEE International Conference on Robotics and Automation, 2004, 5: 4718-4723.

[7] Hu C, Meng MQH, Mandal M. Efficient linear algorithm for magnetic localization and orientation in capsule endoscopy [C] // The 27th Annual International Conference of the IEEE Engineering in Medicine and Biology Society, 2006: 7143-7146.

[8] Hu C, Meng MQH, Mandal M. Ef fi cient magnetic localization and orientation technique for capsule endoscopy [J]. International Journal of Information Acquisition, 2005, 2(1): 23-36.

[9] 胡超, 宋霜, 阳万安, 等. 胶囊内窥镜位置方向磁场定位技术的研究 [J]. 集成技术, 2012, 1(1): 105-113.

[10] Karaboga D. An idea based on honey bee swarm for numerical optimization [R]. Technical report-tr06, Erciyes university, engineering faculty, computer engineering department, 2005.

[11] Karaboga D, Basturk B. On the performance of arti fi cial bee colony (ABC) algorithm [J]. Applied Soft Computing, 2008, 8(1): 687-697.

[12] 席少霖, 赵凤治. 最优化计算方法 [M]. 上海: 上海科学技术出版社, 1983.

[13] Zhu GP, Kwong S. Gbest-guided artificial bee colony algorithm for numerical function optimization [J]. Applied Mathematics and Computation, 2010, 217(7): 3166-3173.

Magnetic Localization and Orientation of Capsule Endoscope Base on Arti fi cial Bee Colony Algorithm

ZHENG Zizhao1HE Xiaoqi2HU Chao2
1( Taiyuan University of Science and Technology, Taiyuan 030024, China )
2(Ningbo Institute of Technology, Zhejiang University, Ningbo 315100, China )

The technology of the capsule endoscope for the detection of the gastrointestinal disease has made a major breakthrough. But the clinical feedback show that some problems are to be solved, including the problem of the location and tracking. Among the possible localization technologies, the magnetic positioning technology with advantages of no need for power and not much space occupation and so on, is very suitable to be applied to the problem of localization of the capsule endoscope. In this paper, for the positioning model of the magnetic dipole based on the magnetic positioning technology, a new algorithm —— hybrid arti fi cial bee colony algorithm was proposed and compared with the arti fi cial bee colony (ABC) algorithm and the nonlinear optimization algorithms that the random complex algorithm and the levenberg - marquart (LM) algorithm. The experimental results show that in terms of the positioning accuracy, the stability and the anti-noise ability, the hybrid arti fi cial bee colony algorithm has better performance than the other three methods.

wireless capsule endoscope; magnet’s localization technique; optimization algorithm; arti fi cial bee colony algorithm

R 445.9

A

2014-07-14

国家自然科学基金项目(61273332)

郑子昭，硕士研究生，研究方向为智能信息与图形图像信息处理；何小其(通讯作者)，博士，讲师，研究方向为机器学习、智能优化和网络安全技术，E-mail：hexq@nit.net.cn；胡超，博士生导师，三江学者特聘教授，研究方向为自动化、机器人控制和传感器技术。