基于最小面积差的三维模型简化算法

祁成武张宇婷舒振宇胡 超徐惠霞

1(浙江大学宁波理工学院信息科学与工程学院 宁波 315100)

2(浙江万里学院数学研究所 宁波 315100)

基于最小面积差的三维模型简化算法

祁成武1张宇婷1舒振宇1胡 超1徐惠霞2

1(浙江大学宁波理工学院信息科学与工程学院 宁波 315100)

2(浙江万里学院数学研究所 宁波 315100)

文章提出了一种基于面积误差度量下的三维网格模型简化方法。该方法通过极小化误差目标函数来简化三角网格模型。算法首先对边遍历，计算每条边的最小面积差；然后对面积差最小的边进行折叠；最后通过求解折叠边的最小面积差，确定新点的坐标。实验结果表明，该算法不仅可以反映局部表面几何变化，还可使模型仍具有较高保真度。最后用实例说明了该方法的有效性。

三维模型简化；QEM；最小面积差

1 引 言

在三维计算机图形学中，一般采用多边形模型来完成单个物体或整个三维环境的绘制。而三角网格模型依靠其运算快速、数学表达简单和便捷等特点脱颖而出，已成为当前图形软件三维建模的基本单元，在图形领域得到了广泛的应用[1]。但是，一个三维物体或场景的高精度三角面片的表示有时需要上百万甚至上亿个三角面片，这对于当前的计算机，特别是显示、传输和存储系统带来了很大的挑战。在这种情况下，通常需要在模型的精度和计算机的计算能力之间进行折衷。即保持模型在可允许的误差范围内变化，运用适当的简化技术来减少原始模型几何元素的数量，从而达到显示和处理的要求和质量。近年来，国内外学者提出了很多网格模型简化算法。这些算法使得大规模三维模型的处理、传输和渲染成为可能，具有重要的意义。本文提出了一种以三维网格模型最小面积变化值为目标的三维模型简化算法。实验结果表明，该算法能够在简化过程中较好地保持面积不变，具有一定的理论意义和实用价值。

现有的网格模型算法大多以特征值、体积和误差等作为简化的目标。它们主要是在保持网格模型的形状或外观基本不变的前提下，尽量减少网格模型的细节信息及多边形数目，从而提高网格模型的显示、传输和计算效率。

在过去的十年里，学者们提出了很多简化算法。其中一类算法[2-9]通过对网格模型进行局部改变，每次改变先删除一部分三角面片，然后用数量更少的三角面片代替，从而完成对三维模型的简化操作。这类方法主要考虑保持模型的逼近误差和拓扑结构，但并不强调三角网格的取样或质量。Garland[10]给出了有关这些方法的详细介绍。

还有一类简化算法[11-15]通过一种称为细分连接性的特殊结构实现模型的简化。这类算法通过不断重复将一个均匀的细分操作符运用到一个较为粗糙的基础网格上来完成简化操作。它的主要优点是可以提供不同级别的细节层次，从而使得多分辨率表达成为可能。但是，其基础网格的构造和顶点取样并不容易控制。

另外一些算法与网格重划有关。先输入一个三角形网格，然后重新取样，得到的新网格形状分布不同但仍近似于同一网格曲面，并满足某些质量要求。运用这种思路的算法[16-19]通常根据局部运算符来进行简化(例如顶点或边折叠)。还有一些方法[20-24]先将原始网格全局参数化，然后再在全部的参数空间中进行重取样，从而实现三维模型的简化。这些方法达到了很好的效果，但也具有计算量大和数值不稳定的缺点。一种改进的思路是用局部参数化方法[25,26]来替代，如 Sifri等[27]与 Peyré 等[28]提出的基于测地路径的网格重划方法。算法结果使得三维网格模型表面上顶点达到一致性分布或者自适应分布。Shu 等[29]通过结合红绿细分技术，并构造三维网格模型上的Voronoi 图以及对偶 Delaunay 三角化，实现了对三维模型的高精度简化。Alliez 和 Gotsman[30]给出了关于这些方法的综述。

2 基于最小面积差的三维模型简化

2.1 二次误差度量(Quadric Error Metrics，QEM)算法[6]简介

QEM 算法以新顶点到其相关平面的距离平方和最小为目标，反复进行边折叠，最终达到简化目的。边折叠操作如图1 所示，将一条边的两个端点 s 和 t 折叠为一个新的顶点 m，同时删除褪化的三角形，这里 m 的位置并不一定是中点，此即一次边折叠操作。

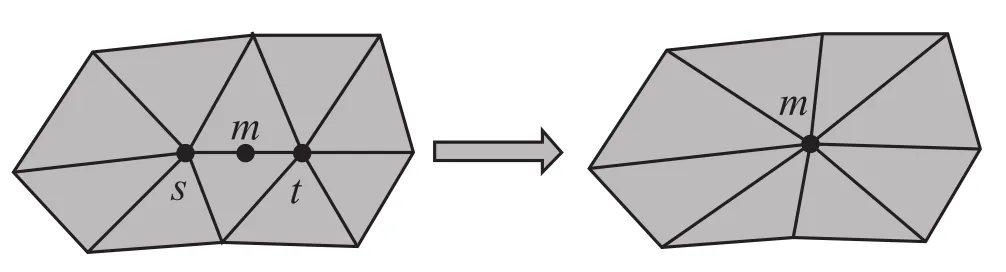
图1 边折叠过程Fig.1. The process of edge collapse

在三维空间中，令 v＝(x, y, z, 1)表示齐次坐标下的顶点，则一个平面可以用方程 pv＝0 表示。其中，p＝(a, b, c, d)T，a, b, c 满足 a2+b2+ c2＝1，是该平面单位法向量的三个分量；d 是固定距离。定义由边折叠引起顶点 v＝(vx, vy, vz, 1)T位置移动导致的二次误差为：

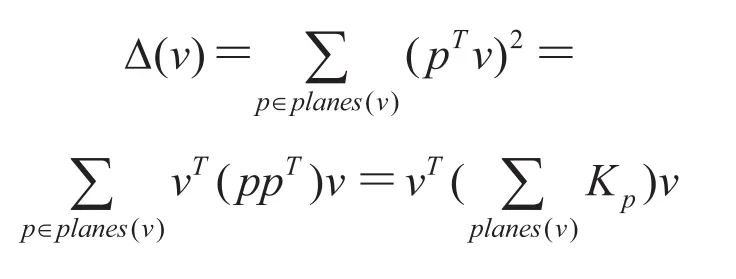
其中，planes(v)表示顶点 v 周围 1-邻域内所有三角面片所在的平面集合；为 v 的二次误差度量矩阵。因为每个初始顶点为周围 1-邻域内三角形的交点，所以初始顶点的二次误差为。当有边折叠操作为了让产生的二次误差最小，最佳的新顶点位置和二次误差分别为：

该算法具有高效且平均误差低等优点。

2.2 加入面积差因素的 QEM 算法

在 QEM 算法中，可以发现有两个关键的边折叠因素：一个是如何对折叠边排序，另一个是如何选择新顶点的位置。这两个因素决定了折叠简化后是否能得到优化的新网格。

网格折叠简化实质上可认为是一个优化问题。解决该问题的常用方法是定义目标函数，简化后的网格是目标函数的最优解，因此网格简化的关键是如何建立该目标函数。显然，目标函数应是表达新旧两个网格间差别的函数：通过极小化目标函数得到新顶点的位置，并使新旧两个网格间差别在某种意义下达到最小[31]。

2.2.1 定义面积差

本文的目标函数采用网格的平方面积变化作为衡量模型间差别的标准：使得三维网格简化前后的面积改变趋向于最小，同时又保持模型的特征基本不变。

图2 表明了在确定折叠边为 O1O2后，对边O1O2的边折叠并确立新点 C 的过程。其中，S1为含点 O1的三角面片的面积和；S2为含点 O2的三角面片的面积和；SC为含新点 C 的三角面片的面积和。 要使边折叠前后模型表面积变化越小，即使的值越小。

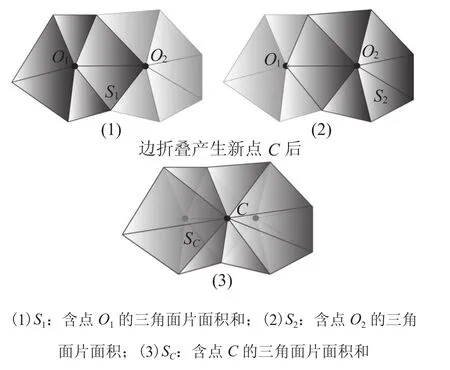
图2 边折叠过程Fig.2. The process of edge collapse

2.2.2 子算法一：确定折叠边

(1)按模型边顺序遍历所有边；

(2)对每条边计算其最小面积差；

(3)得到最小的最小面积差，并以该边为折叠边；

(4)边折叠后得到边的顺序、折叠边的最小面积差及新点坐标；

(5)一次边折叠结束。

2.2.3 子算法二：确定边折叠后新点的位置

图3 为确定边折叠后新点的最佳位置示意图。

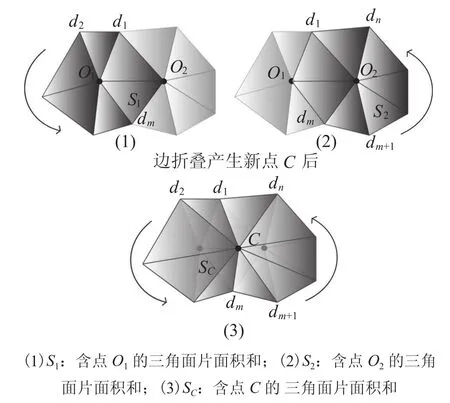
图3 确定边折叠后新点的最佳位置Fig.3. The optimal location of the new point after edge collapsing

如图3(1)中所示，可得

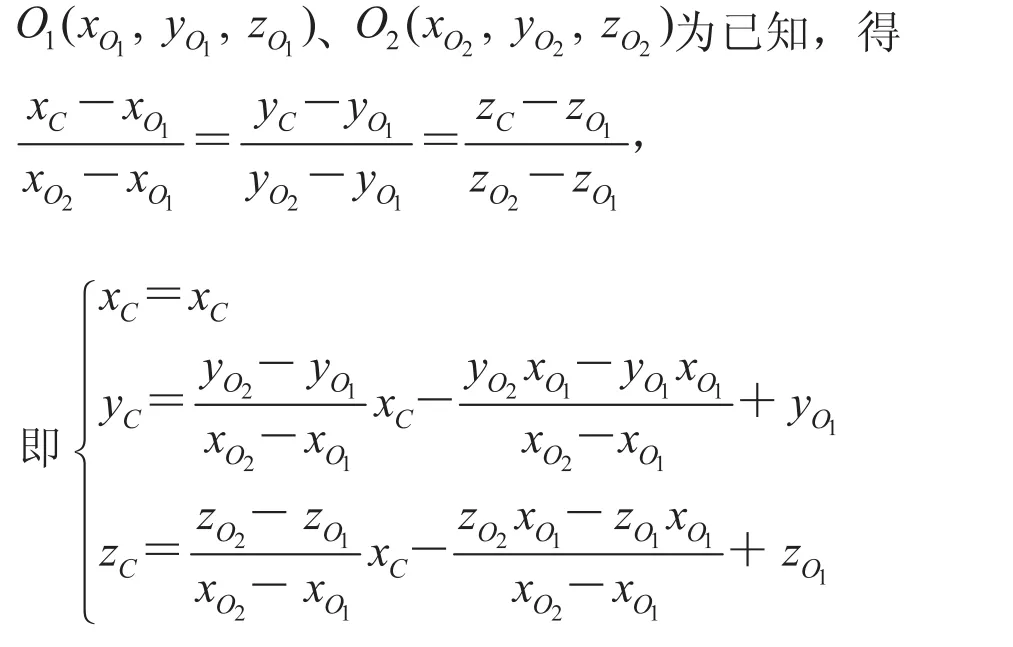
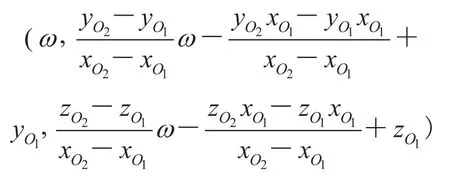
3 实验与讨论

3.1 实验结果

本节给出的实例是在 Intel(R) Core(TM)2 Duo CPU，2.00 G 内存 PC 上用 Visual Studio 2012 实现的。本文提出的网格简化算法基于三角形网格折叠，比较的模型实例是模型 Eight。

图4 给出了本文算法在 Eight 模型上的简化效果图。从图4 可以看出，本文算法选择边折叠前后面积变化小的边开始折叠。同时也可以看出，该模型数据有着明显的简化效果，证明了该算法的可行性和有效性。

3.2 面积对比

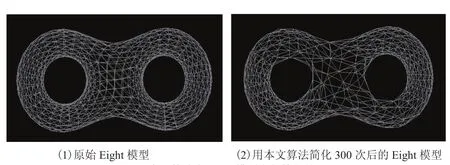
图4 本文算法在 Eight 模型上的简化效果图Fig.4. The effect of the simpli fi ed Eight model by using our method

图5 Seahorse 模型简化 90% 对比图Fig.5. The comparison results of the 90% simpli fi ed Seahorse model by using our method and the QEM algorithm

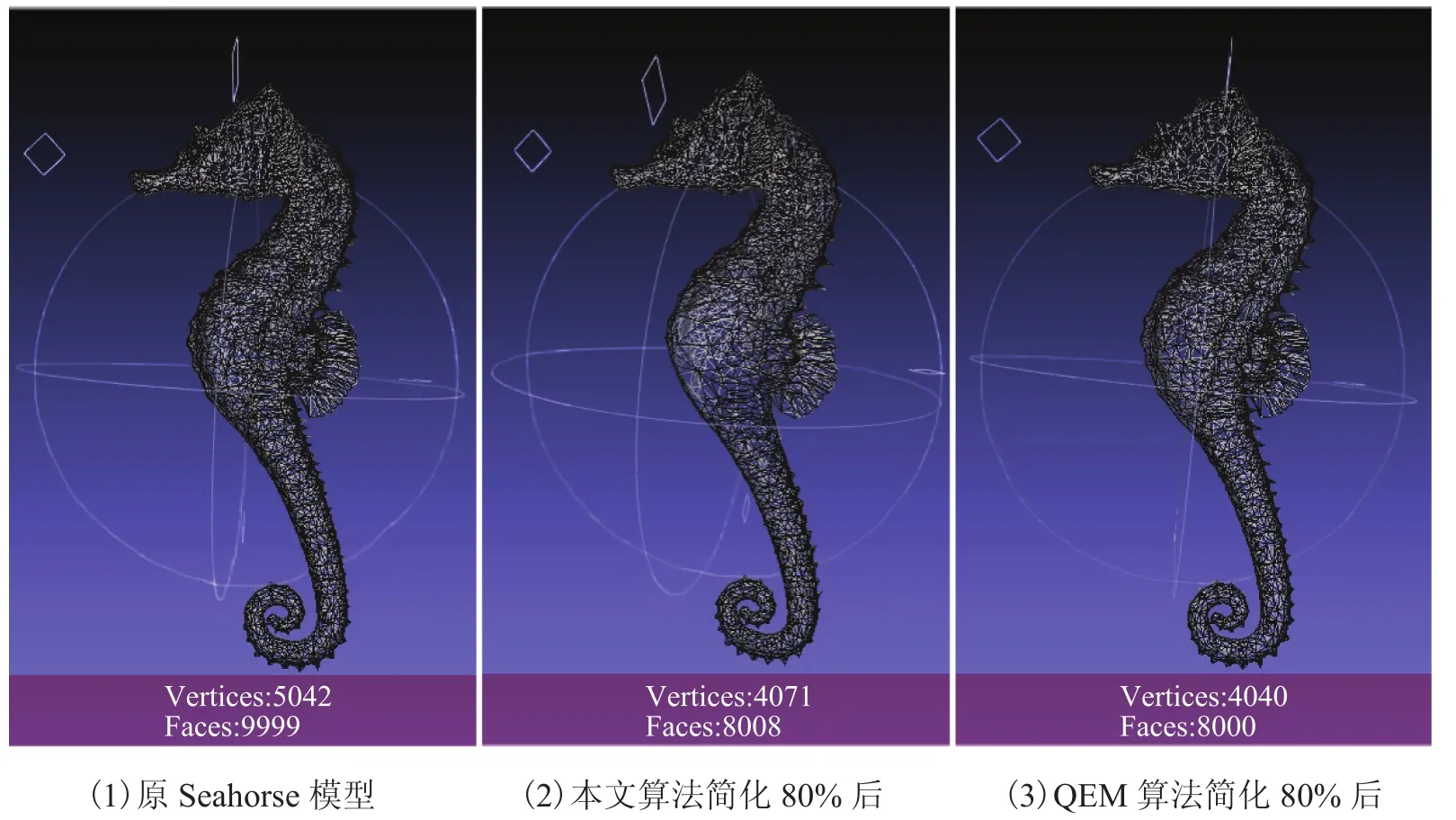
图6 Seahorse 模型简化 80% 对比图Fig.6. The comparison results of the 80% simpli fi ed Seahorse model by using our method and the QEM algorithm

为对比模型简化后的表面积维持效果，本文在模型 Seahorse(5042 个顶点，9999 个三角面片)上进行了算法实验和比较 ，结果见图5 和图6。该模型的点较为均匀，可以看出在采集点的时候属于均匀分布采集的方法。图5 和图6 显示，较为平整的面主要集中在 Seahorse 模型的肚子部位。从图5 和图6 中的(2)小图，即本文算法简化后的效果图，可以发现，Seahorse 肚子上明显点减少了，而图5 和图6 中的(3)小图中，Seahorse的肚子上点无明显减少。

从表1 可以看出，对三维网格模型进行相同比例的简化后，本文方法产生的表面积误差要远小于 QEM 算法。

第二个模型实例是模型 RockerArm(500 个顶点，1000 个三角面片)。与第一个的区别在于，该模型数据较小，可以考察在较小模型下，本文算法的面积误差有效性能否保持。

对 RockerArm 模型分别运用本文算法与QEM 算法，其模型简化对比如图7 所示，网格简化表面积维持率比较如表2 所示。

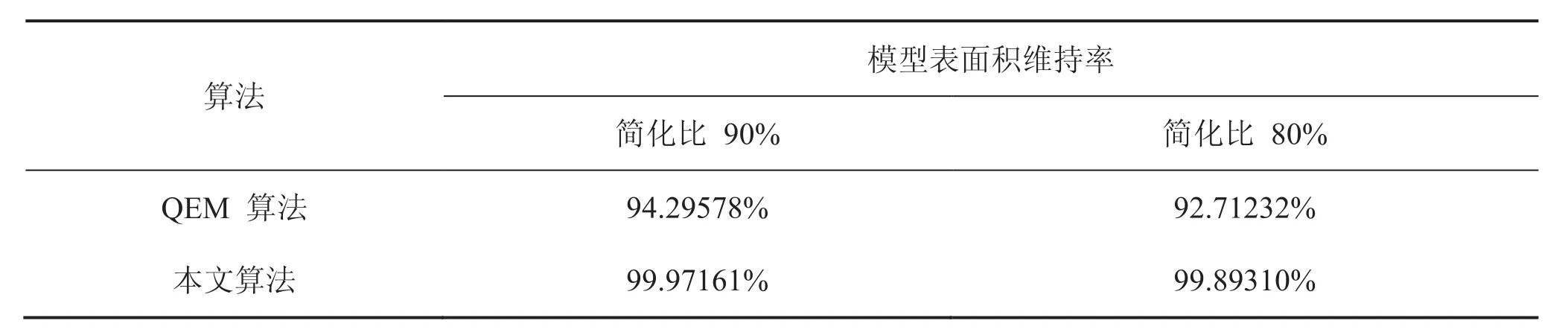
表1 Seahorse 模型简化表面积维持率比较Table1. A comparison between the retention rate of the surface area after simplifying the model of Seahorse from using the QEM and our method

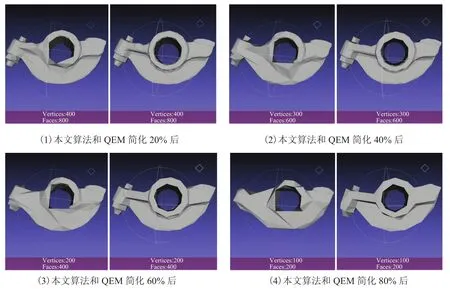
图7 RockerArm 模型简化对比图Fig.7. The comparison results of the RockerArm model

从表2 可以看出，对网格进行相同比例的简化后，本文方法产生的表面积误差要远小于QEM 算法。

同时，当模型数据很少时，本文算法对模型的特征保持率较低。但从另一面来讲，运用到实际中，如果模型较小，那其需要简化的概率也极小。一般只有当模型数据非常大时，才需要运用到简化算法。

3.3 距离误差对比

本文在 Seahorse 模型(5042 个顶点，9999 个三角面片)上对本文算法和 QEM 算法简化结果的Hausdorff 距离进行了对比。

为了比较两种方法在简化过程中网格模型的 Hausdorff 距离作为误差标准进行比较，Hausdorff 距离由下式定义，定义如下：

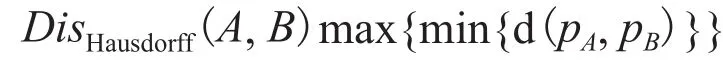
其中，d(pA, pB)为点与点之间的距离。

从表3 可以看出，运用这两种算法分别对网格进行相同比例的简化后，本文算法产生的平方体积误差要大于采用 QEM 算法的所产生的平方体积误差。虽然如此，但是从 Hausdorff 距离的比较结果来看，在简化比率不是很大的情况下，本文算法具有较好的简化效果。

3.4 运行时间对比

使用模型 RockerArm 来进行运行时间对比。QEM 作为模型简化中常用的方法，其主要原因就是其简化效率高，而简化后模型表面特征保持良好。本文算法与 QEM 网格简化运行时间比较如表4 所示。

从表4 可以看出，本文算法和 QEM 算法的运行时间较为接近。说明本文算法具有较好的运算效率和可操作性。

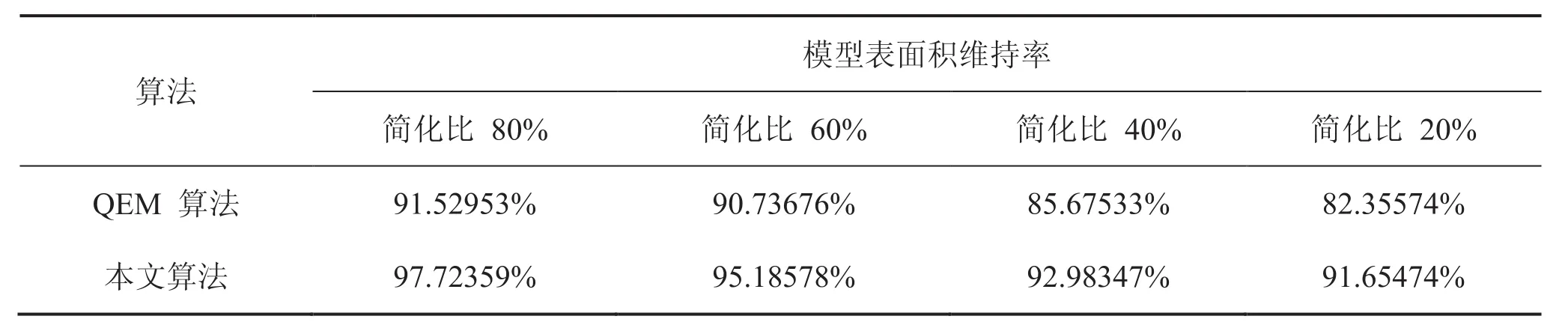
表2 RockerArm 模型简化表面积维持率比较Table2. A comparison of the retention rate of the surface area after simplifying the RockerArm by using the QEM algorithm and our method

表3 Seahorse 模型简化的 Hausdorff 距离比较Table3. A comparison of the Hausdorff distances after simplifying the model of Seahorse by using the QEM algorithm and our method

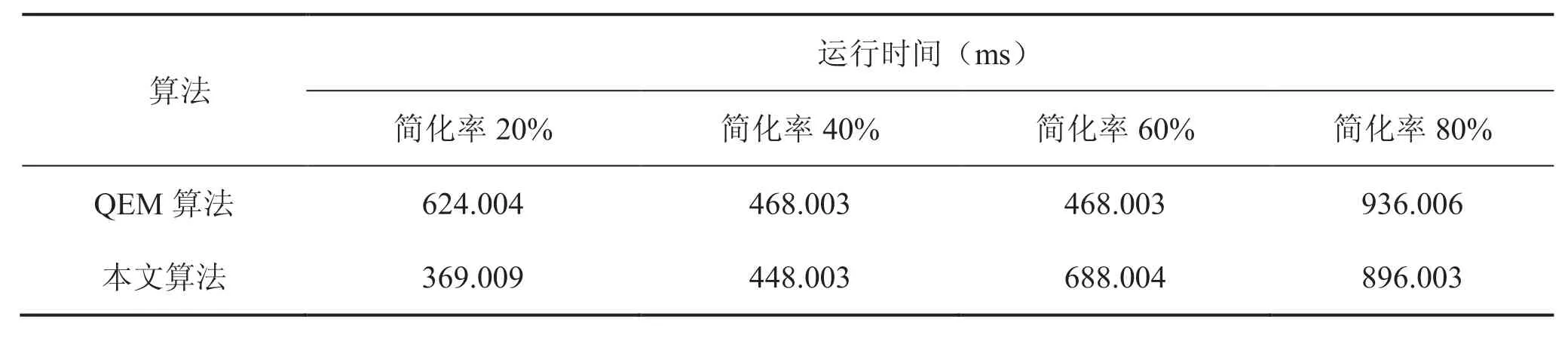
表4 网格简化运行时间比较Table4. A comparison of the running time of mesh simpli fi cation by using the QEM algorithm and our method

4 结 论

本文提出了一种基于面积误差度量下的三维网格模型简化方法。该方法通过极小化误差目标函数来简化三角网格模型：首先对模型中所有边进行遍历，并对每条边计算其最小面积差，折叠其中最小结果的边，之后通过求解最小面积差，确定新点的坐标。从代码编写后生成的效果图可以看出，改进后的算法不仅可以反映局部表面几何变化，同时模型仍具有较高保真度。本文最后用实例说明本文方法的有效性。

随着三维打印等技术的出现，更多的实际应用场合为了追求三维效果，开始使用三维模型，三维模型简化也会有越来越多的应用机会。从目前国内外研究及应用来看，虽然已经有大量网格简化的相关研究工作，但是还没有一种适合所有应用的网格简化，绝大多数算法都是针对具体问题提出的。另外不管哪种网格简化算法都有其优劣性，也许在不久的将来，随着硬件软件的更新换代，能实现一种智能算法，可以判断模型简化的倾向性并能将多种经典的简化算法融合在一起，同时仍能保持高速运算。

[1] 丁大伟, 邵新宇, 邱浩波, 等. 多边形网格模型简化算法综述 [J]. 机械设计与制造, 2007, 9: 181-183.

[2] Schroeder WJ, Zarge JA, Lorensen WE. Decimation of triangle meshes [C] // Proceedings of the 19th Annual Conference on Computer Graphics and Interactive Techniques, 1992: 65-70.

[3] Cohen J, Varshney A, Manocha D, et al. Simpli fi cation envelopes [C] // Proceedings of the 23rd Annual Conference on Computer Graphics and Interactive Techniques, 1996: 119-128.

[4] Hoppe H. Progressive meshes [C] // Proceedings of the 23rd Annual Conference on Computer Graphics and Interactive Techniques, 1996: 99-108.

[5] El-Sana J, Varshney A. Controlled simplification of genus for polygonal models [C] // Proceedings of the 8th Conference on Visualization, 1997: 403-410.

[6] Garland M, Heckbert PS. Surface simplification using quadric error metrics [C] // Proceedings of the 24th Annual Conference on Computer Graphics and Interactive Techniques, 1997: 209-216.

[7] Lindstrom P, Turk G. Fast and memory efficient polygonal simplification [C] // Proceedings of the Conference on Visualization, 1998: 279-286.

[8] Kobbelt L, Campagna S, Seidel H. A general framework for mesh decimation [C] // Proceedings of Graphics Interface, 1998: 43-50.

[9] Zelinka S, Garland M. Permission grids: practical, error-bounded simpli fi cation [J]. ACM Transactions on Graph, 2002, 21(2): 207-229.

[10] Garland M. Multiresolution modeling: survey & future opportunities [C] // State of the Art Reports, 1999: 111-131.

[11] Eck M, DeRose T, Duchamp T, et al. Multiresolu-tion analysis of arbitrary meshes [C] // Proceedings of the 22nd Annual Conference on Computer Graphics and Interactive Techniques, 1995: 173-182.

[12] Lee AWF, Sweldens W, Schröder P, et al. MAPS: multiresolution adaptive parameterization of surfaces [C] // Proceedings of the 25th Annual Conference on Computer Graphics and Interactive Techniques, 1998: 95-104.

[13] Kobbelt LP, Vorsatz J, Labsik U, et al. A shrink wrapping approach to remeshing polygonal surfaces [J]. Computer Graphics Forum, 1999, 18(3): 119-130.

[14] Guskov I, Vidimce K, Sweldens W, et al. Normal meshes [C] // Proceedings of the 27th Annual Conference on Computer Graphics and Interactive Techniques, 2000: 95-102.

[15] Hormann K, Labsik U, Greiner G. Remeshing triangulated surfaces with optimal parameterizations [J]. Computer-Aided Design, 2001, 33(11): 779-788.

[16] Turk G. Retiling polygonal surfaces [J]. ACM SIGGRAPH Computer Graphics, 1992, 26(2): 55-64.

[17] Hoppe H, DeRose T, Duchamp T, et al. Mesh optimization [C] // Proceedings of the 20th Annual Conference on Computer Graphics and Interactive Techniques, 1993: 19-26.

[18] Frey PJ, Borouchaki H. Geometric surface mesh optimization [J]. Computing and Visualization in Science, 1998, 1(3): 113-121.

[19] Frey PJ. About surface remeshing [C] // Proceedings of the 9th International Meshing Roundtable, 2000: 123-136.

[20] Alliez P, Meyer M, Desbrun M. Interactive geometry remeshing [J]. ACM Transactions on Graphics, 2002, 21(3): 347-354.

[21] Alliez P, Cohen-Steiner D, Devillers O, et al. Anisotropic polygonal remeshing [J]. ACM Transactions on Graphics, 2003, 22(3): 485-493.

[22] Alliez P, Verdiere EC, Devillers O, et al. Isotropic surface remeshing [C] // International Conference on Shape Modeling and Applications, 2003: 49-58.

[23] Alliez P, Verdiere EC, Devillers O, et al. Centroidal Voronoi diagrams for isotropic surface remeshing [J]. Graphical Models, 2005, 67(3): 204-231.

[24] Gu X, Gortler SJ, Hoppe H. Geometry images [J]. ACM Transactions on Graphics, 2002, 21(3): 355-361.

[25] Surazhsky V, Gotsman C. Explicit surface remeshing [C] // Proceedings of the 2003 Eurographics/ACM SIGGRAPH Symposium on Geometry Processing, 2003: 20-30.

[26] Surazhsky V, Alliez P, Gotsman C. Isotropic remeshing of surfaces: a local parameterization approach [C] // Proceedings of the 12th International Meshing Roundtable, 2003: 215-224 .

[27] Sifri O, Sheffer A, Gotsman C. Geodesic-based surface remeshing [C] // International Meshing Roundtable, 2003: 189-199.

[28] Peyré G, Cohen L. Geodesic remeshing using front propagation [J]. International Journal of Computer Vision, 2006, 69(1): 145-156.

[29] Shu Z, Wang G, Dong C. Adaptive triangular mesh coarsening with centroidal Voronoi tessellations [J]. Journal of Zhejiang University Science A, 2009, 10(4): 535-545.

[30] Alliez P, Gotsman C. Recent advances in compression of 3D meshes [C] // Proceedings of the Symposium on Multiresolution in Geometric Modeling, 2003: 3-26.

[31] 周元峰, 张彩明, 贺平. 体积平方度量下的特征保持网格简化方法 [J]. 计算机学报, 2009, 32(2): 205-206.

3D Model Simpli fi cation Algorithm Based on Minimum Surface Area Error

QI Chengwu1ZHANG Yuting1SHU Zhenyu1HU Chao1XU Huixia2
1( School of Information Science and Engineering, Ningbo Institute of Technology, Zhejiang University, Ningbo 315100, China )
2(Institute of Mathematics, Zhejiang Wanli University, Ningbo 315100, China )

A new algorithm for 3D mesh simplification based on minimum surface area error was presented in this paper. The algorithm simpli fi es 3D models by minimizing an error objective function. Firstly, the algorithm used the edge traversal algorithm for calculating the minimum area of each edge. Then the vertex coordinates of those new points were determined by fi nding the minimum surface area error. The results of our experiment show that our algorithm can not only re fl ect the local surface geometry changes, but also keep the model in a relatively high fi delity. Experimental results for the effectiveness of the algorithm were also presented.

3D model simpli fi cation; QEM; minimum surface area error

TP 391.72

A

2014-07-22

国家自然科学基金(11226328，61273332，61303144)；浙江省自然科学基金(LY13F020018)；宁波市自然科学基金(2013A610096)

祁成武，硕士研究生，研究方向为计算机图形学；张宇婷，本科生，研究方向为计算机图形学；舒振宇(通讯作者)，博士，副教授，研究方向为计算机图形学和计算机辅助几何设计等，E-mail：shuzhenyu@163.com；胡超，博士，教授，博士生导师，三江学者特聘教授，研究方向为自动化、机器人控制和传感器技术等；徐惠霞，博士，副教授，研究方向为计算机辅助几何设计。