MATLAB在自适应电力系统稳定器中的智能优化分析
2014-07-19葛俊峰
葛俊峰
(集宁师范学院 科研设备处, 内蒙古 乌兰察布 012000)
MATLAB在自适应电力系统稳定器中的智能优化分析
葛俊峰
(集宁师范学院 科研设备处, 内蒙古 乌兰察布 012000)
为提升电力系统稳定器的使用效果,分析了影响低频振荡的因素,并对自适应电力系统稳定器的相关配置进行了分析,在此基础上,并以 MATLAB 为工具,研究了自适应电力系统稳定器智能调节分析的优化方法.
电力系统;稳定器;自适应;智能优化
随着我国经济、社会的不断发展,人们对电力的使用需求越来越高.为满足社会不断增长的电力需求,超高压远距离输电线路及其相应的发电设备不断地被开发出来,电力系统行业也逐渐向着长距离、大容量、高复杂性的方向发展.由于电力系统的不断发展,相应的问题也逐渐显现,其中最为明显的是低频振荡对电力系统整体安全造成的威胁.如何对电力系统进行设计与改进,从而能够在方便管理的前提下,有效解决电力系统低频振荡问题,是目前行业内亟待解决的关键性问题.虽然电力系统稳定器的开发对于低频振荡有一定的缓解作用,但由于电力系统本身的复杂性,仅仅依靠人工对电力系统稳定器进行整定与控制,一方面缺乏准确性,另一方面,在安全性、快捷性上也存在诸多方面的不足.
鉴于此,本文就自适应电力系统稳定器展开研究,并以MATLAB为研究手段,对其参数的智能优化进行了仿真与分析.成果有利于新一代的电力系统稳定器的研发.
1 电力系统低频振荡探讨
在不同的电网之间,发电机通过相应的输电线路平行地运行.在这种情况下,当扰动出现时,发电机转子之间会出现相互的摆动现象,这种摆动的现象在一定条件下会引发持续的振荡,进而引起低频振荡的发生.电力系统低频振荡是较为常见影响电力系统安全性的因素.它主要由以下几个方面的因素引起:
(1)电网之间的弱联系.两个独立电网之间联络回路较少、导线截面较小以及阻抗过大都会引起电网之间弱联系的出现.
(2)长线路、远距离输电的影响.由于供电的需求,长线路、远距离的输电系统往往在所难免,在这样的系统中,低频振荡是较为常见的现象.
(3)励磁系统的影响.低频振荡往往更容易发生在高放大倍数的励磁系统的电力系统中,对电力系统的安全造成隐患.
归结起来,电力系统产生低频振荡的原因为:电力系统机械模式阻尼较小造成系统振荡无法平息,从而引起低频振荡;电力系统在励磁控制过程中,励磁电流对励磁电压产生的之后作用导致了低频振荡的产生;由于励磁系统变化时间过短造成的电力系统扰动过大从而引起低频振荡;电力系统本身具有非线性特性,这种非线性特性在较小的扰动下容易使电力系统特性和状态发生变异,从而导致低频振荡的发生;人为的不适当控制引起的电力系统扰动,从而诱发低频扰动.
2 自适应电力系统稳定器的构建
为了更为有效地解决电力系统低频振荡问题,从上世纪 50年代起,自适应电力系统稳定器就被研发出来.自适应电力系统稳定器大致可分为自动校正稳定器、模型参考自适应稳定器以及其他类型自适应稳定器.在这其中,自校正稳定器是一种将模型参数的预估和控制器参数的设计相结合起来的、综合性的稳定器自适应技术.这种技术具有设计灵活、操作简单的优势,在电力系统中得到了较为广泛的应用.
本文所描述的自适应电力系统稳定器是基于带有遗忘因子的递推最小二乘法构建的.其方法为在原有递推运算时,对数据进行相应的加权计算,从而使相应的数据作用得到突出,从而达到“遗忘”的目的.其具体的算法为:以 λ(0<λ<1)为加权因子(遗忘因子),在相应的数据得以测出时,以该数值乘以遗忘因子,以达到加权的目的.
2.1 自适应稳定器的电力系统结构
自适应电力系统稳定器的构成一般分为:系统模型、控制器与参数识别器.在这其中,系统模型是自适应电力系统稳定器的基础,它是以数学方法将电力系统数值化地表示出来,并对其结构进行验证与检测,从而得到相关数据.参数识别器的主要功能是对自适应稳定器的参数进行计算,在其中,所采用的算法是带有遗忘因子 λ 的递推算法.控制器是在不断调整极点移动配置控制的基础上开发的能够直接对系统进行控制的应用程序.自适应电力系统稳定器的各个组成部分不是独立地进行运作,而是作为一个有机的整体进行运转,以达到降低低频振荡的目的.
2.2 自适应电力系统稳定器系统模型的选择
电力系统本身是一个极为复杂的非线性的体系,在自适应电力系统稳定器计算的过程中,必须考虑其参数的未知性与时变性.针对自适应电力系统稳定器的非线性状况,很难用较为精确的数值模型对其进行仿真.在模型选择时,应从部分出发,将系统的整体分割为不同的小系统,在各个小系统中利用线性模型进行表示.
2.3 自适应电力系统稳定器闭环参数的识别
就自适应稳定器而言,其参数识别器是在闭环条件下展开运行的.在这种条件下,参数识别器接收到的往往是一组特征并不明显的数据,利用这种数据,很难对系统参数进行估计.因此,在实际应用过程中,往往在电力系统输入或输出端口进行相应的信号扰动,从而使得系统的行为不断地得到激励.扰动信号应具有足够的频率带,以使其能够涵盖系统的频率.另外,扰动信号应不影响系统本身的合理运行.因此,扰动信号应具有能够实时调节或自动调节的功能,从而使得参数识别器的使用效果更为优良.
3 基于 MATLAB 的自适应电力系统稳定器优化分析
作为一种具备精确计算与数值仿真功能的高性能交互式计算机语言平台,MATLAB为电力系统的运算与仿真提供了专有的 SimPowerSystems模型库,主要由电源库、电机模型和测量元件等相关部分组成.在 SimPowerSystems模型运算过程中,用户可将不同的元件进行连接,并通过相应地语言进行控制,以达到模拟仿真的目的.
3.1 带 λ 参数识别器的实现
本文中,以三阶离散模型对电力系统进行表征.在模型中,引入权值遗忘因子 λ,并采用 S-Function Builder工具对相应的识别器函数进行编写.在此基础上,将编译完成的S-Function进行封装.为保证自适应电力系统稳定器仿真过程中参数识别器计算仿真的准确性,本文在 MATLAB的基础上研发了相应的计算验证程序.验证结果表明,当时间为0.09s时,识别器能够对参数进行识别,模型识别参数与实际参数的相关性良好.
3.2 极点移动配置控制器的实现
自适应电力系统稳定器 MATLAB仿真中机电移动配置控制器由参数估计值确定,其设计控制律如式(1)所示.

在式(1)的基础上,通过数值运算,得到控制器的控制量如式(2)所示.
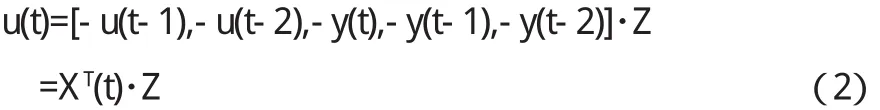
在 MATLAB中,自适应电力系统稳定器极点移动配置控制器由 MATLAB中的 Fen模块构建,并最终封装成一个控制模型.
3.3 移动因子自动调节控制仿真
不同的移动因子参数输入能够获得不同的控制仿真效果.当移动因子为1时,控制器无输出;而当移动因子为0.9995-0.9998时,控制器的输出对于改良低频振荡能够取得较为良好的效果.由此看来,移动因子的微小变化对控制器有较大的影响.本文在此基础上,研究了移动因子的自动调节控制方法,以控制相应的参数数值在一定范围以内,从而达到抑制低频振荡的目的.在 MATLAB仿真中,将移动因子设定在一定合理的范围,当自适应稳定器输出超出范围后,通过程序的自动识别,可将移动因子进行自动调节,以完成对输出结果控制的目的.
4 结语
自适应电力系统稳定器是抑制低频振荡的较为直接也较为有效的方法.为提升电力系统稳定器的使用效果与操控效果,本文在对低频振荡产生因素进行分析的基础上,对自适应电力系统稳定器的相关参数与配置进行了构建,并以MATLAB为工具,研究分析了自适应电力系统稳定器智能调节分析的优化方法.成果有利于自适应电力系统稳定器的不断完善与推广应用.
〔1〕王海风,韩祯祥,B.W.Hogg.自适应电力系统稳定器设计的频域方法[J].中国电机工程学报,1992(06):3-12.
〔2〕杨祉涵,张雪霞,李奇,邓美玉.基于自适应差分算法的电力系统稳定器参数设计[J].四川电力技术,2011(03):26-28+72.
〔3〕杨敏虹.电力系统稳定器参数选择和优化分析[J].电工技术,2001(09):42.
〔4〕刘杨名,严正.基于自适应遗传算法的系统PSS参数优化[J].中国农村水利水电,2007(11):129-132+136.
〔5〕温嘉斌,汤伟.基于MATLAB的PSS的仿真分析[J].信息技术,2010(04):75-78.
TM44
A
1673-260X(2014)08-0040-02
内蒙古教育厅科研项目(NJZC14292)阶段性成果
