On the Strong Rates of Convergence for Arrays of Rowwise Extended NegativelyDependent Random Variables

ZHENG Lu-lu,XU Chen,HUANG Xu-feng,WANG Xue-jun

(School of Mathematical Science,Anhui University,Hefei 230601,China)

On the Strong Rates of Convergence for Arrays of Rowwise Extended Negatively
Dependent Random Variables

ZHENG Lu-lu,XU Chen,HUANG Xu-feng,WANG Xue-jun

(School of Mathematical Science,Anhui University,Hefei 230601,China)

A general result on the strong convergence rate and complete convergence for arrays of rowwise extended negatively dependent random variables is established.As applications,some well-known results on negatively dependent random variables can be easily extended to the case of arrays of rowwise extended negatively dependent random variables.

extended negatively dependent random variables;negatively dependent;complete convergence

§1.Introduction

The concept of complete convergence for a sequence of random variables was introduced by Hsu and Robbins[1]as follows.A sequence{Un,n≥1}of random variables converges completely to the constant θ,if

In view of the Borel-Cantelli lemma,this implies that Xn→θ almost surely.Therefore, the complete convergence is a very important tool in establishing almost sure convergenceof summation of random variables as well as weighted sums of random variables.Moreover, Hsu and Robbins[1]proved that the sequence of arithmetic means of independent identically distribution(i.i.d)random variables converges completely to the expected value if the variance of the summands is f i nite.Erd¨os[2]proved the converse.The result of Hsu-Robbins-Erd¨os is a fundamental theorem in probability theory and this result has been generalized and extended in several directions,see Gut[3],Hu et al[45],Chen et al[6],Sung[78],Wang et al[9],Zhou et al[10],Wu[1113],Shen[1415]and so forth.The main purpose of this investigation is to provide the complete convergence results for weighted sums of arrays of rowwise extended negatively dependent(END,in short)random variables.The material in this note is closely related to what proposed by Chen et al[6]and Qiu et al[16].

To proved the main results,we need some notions and some important lemmas.

The following dependence structure was introduced by Liu[17].

Def i nition 1.1We call random variables{Xn,n≥1}END if there exists a constant M＞0 such that both

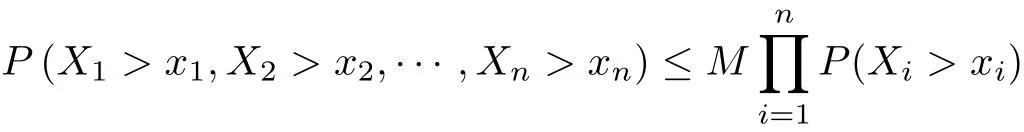
and

hold for each n≥1 and all real numbers x1,x2,···,xn.

In the case M=1,the notion of END random variables reduces to the well-know notion of so-called negatively dependent(ND)random variables,which was introduced by Lehmann[18](cf. also Joag-Dev and Proschan[19]).As it mentioned in Liu[17],the END structure is substantially more general than ND structure,it can ref l ect not only a negative dependence structure but also a positive one,to some extent.Liu[17]pointed out that the END random variables can be taken as negatively or positively dependent and provide some interesting examples to support this idea.Joag-Dev and Proschan[19]also pointed out that negatively associated(NA)random variables must be ND and ND is not necessarily NA,thus NA random variables are END. For more details about END random variables,one can refer to Liu[20],Shen[21],Wang and Wang[22],and so forth.

Throughout this article,let{Xni,1≤i≤kn,n≥1}be a sequence of END random variables def i ned on a f i xed probability space(Ω,F,P)with the same M in each row,where{kn,n≥1} be a sequence of positive integers such that limn→∞kn=∞.Denote X+=max{0,X}, logx=max{1,lnx},where lnx denotes the natural logarithm.C and M will represent positive constants which values may change from one place to another.For t＞0,letn≥1.

§2.Preliminary Lemmas

The following there lemmas provide us some useful properties for END random variables. The f i rst one is a basic property for END random variables,which was obtained by Liu[20].

Lemma 2.1[20]Let random variables X1,X2,···,Xnbe END.

(i)If f1,f2,···,fnare all nondecreasing(or nonincreasing)functions,then random variables f1(X1),f2(X2),···,fn(Xn)are END.

(ii)For each n≥1,there exists a constant M＞0 such that

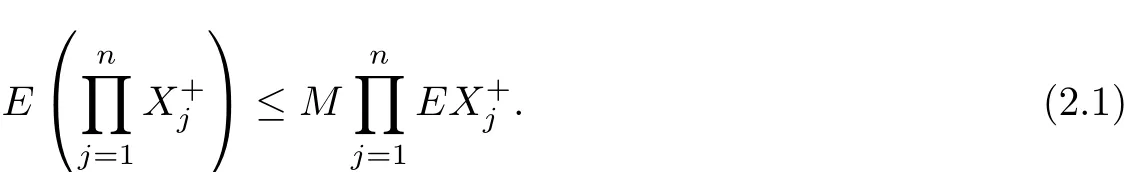
The next one is a simple corollary of the previous one.For the proof,one can refer to Shen[21].

Lemma 2.2[21]Let{Xn,n≥1}be a sequence of END random variables and{tn,n≥1} be a sequence of nonnegative numbers(or nonpositive numbers),then for each n≥1,there exists a constant M＞0 such that

As a byproduct,for any t∈ℝ,

The last one is a very important probability inequality for END random variables,which was obtained by Shen[21].

Lemma 2.3[21]Let{Xn,n≥1}be a sequence of END random variables with EXi=0 for each i≥1.Then for any h,x,y＞0,there exists a positive constant M such that

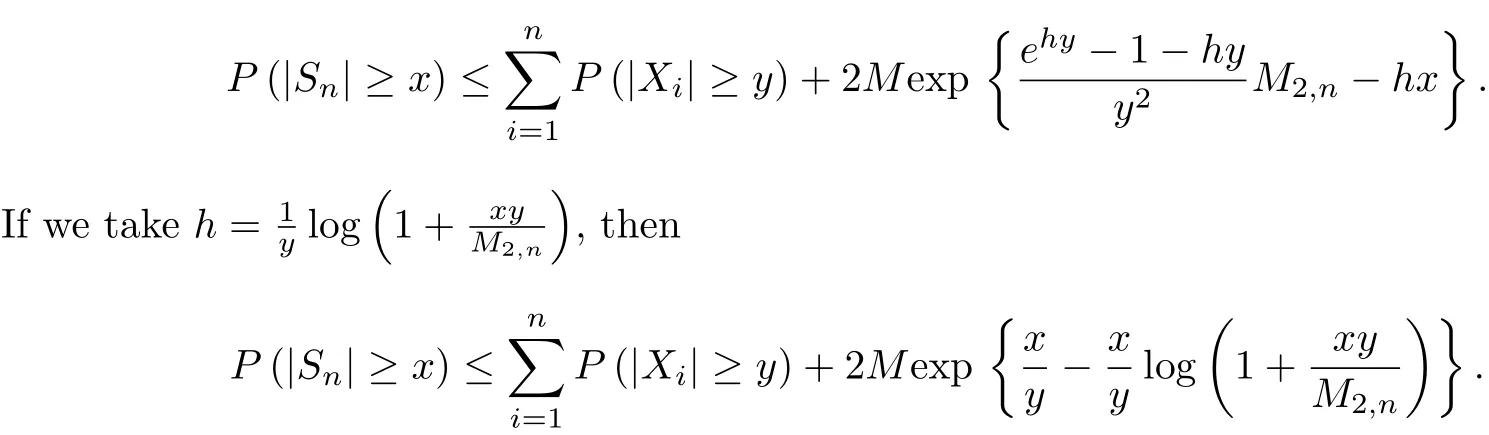
§3.Main Results and Their Proofs

In this section,we will study the complete convergence of weighted sums for arrays of rowwise END random variables,which generalize the corresponding ones for ND random variables.

Theorem 3.1Let{Xni,1≤i≤kn,n≥1}be an array of rowwise END random variables. Assume that{ani,1≤i≤kn,n≥1}is an array of real numbers and{an,n≥1}is a sequence of positive constants.If for any ε＞0 and some δ＞0,

and there exists q≥1 such that

Then

ProofNote that for any f i xed ε＞0 and n≥1,

By condition(3.1),it suffices to show that

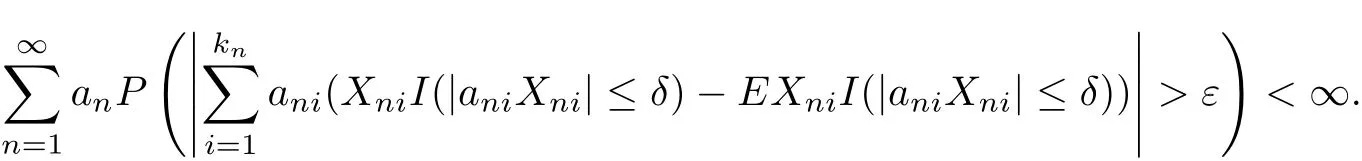
Denote for 1≤i≤knand n≥1,

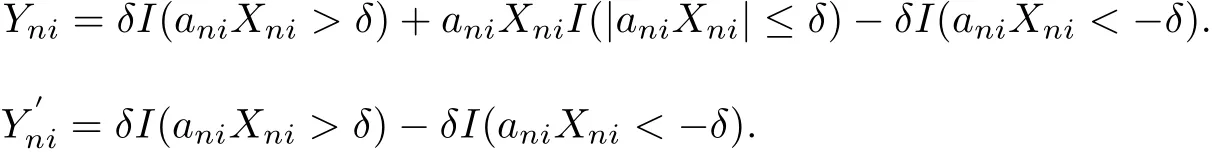
We have

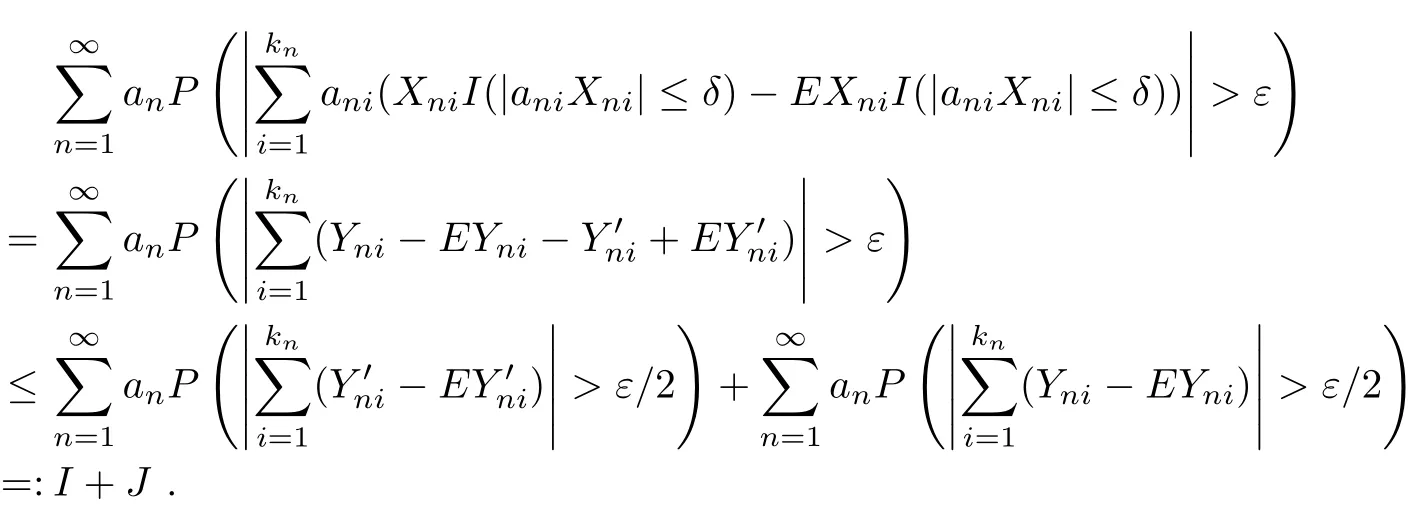
For I,by Markov’s inequality and condition(3.1),we have

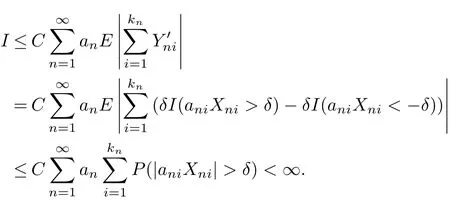
For any y＞0,let d=min{1,y/6δ},

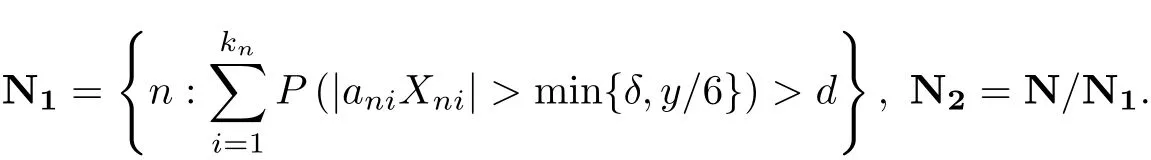
Note that

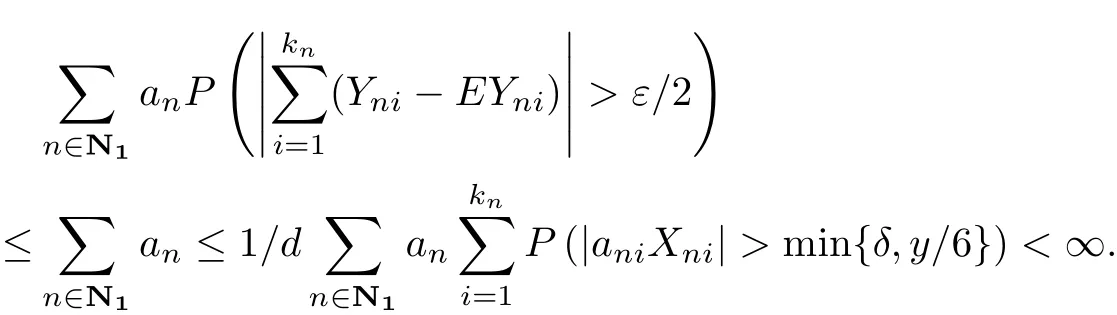
Hence,it is sufficient to prove that when n∈N2,it’s also true.By Lemma 2.1,we know that {Yni−EYni,1≤i≤kn,n≥1}is an array of rowwise END random variables.By Lemma 2.3 we have that

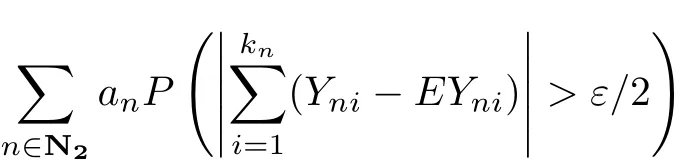
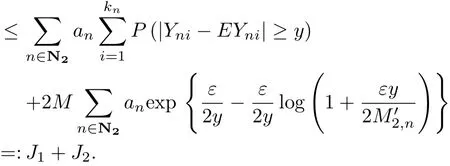
Note that for n∈N2,

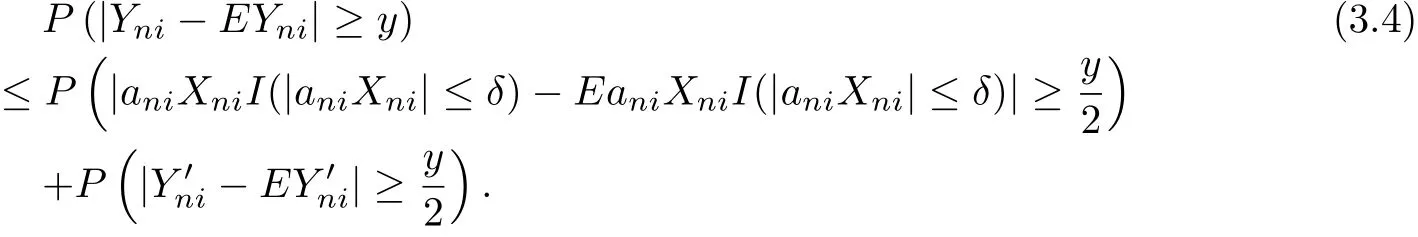
It is easy to check that for n∈N2,

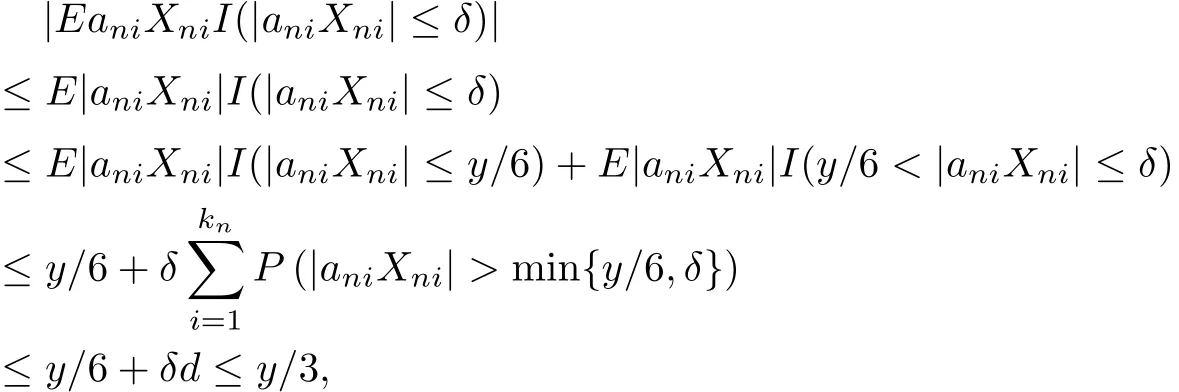
which implies that for n∈N2,

Therefore,by(3.1)we obtain

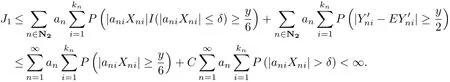
Now we prove J2＜∞.When n∈N2,we have that≤1.Let y=ε/2q,by conditions(3.1)and(3.2),we obtain

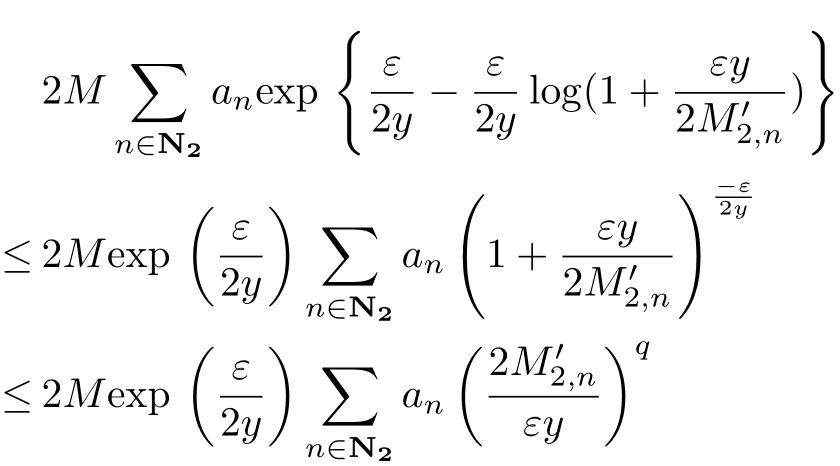
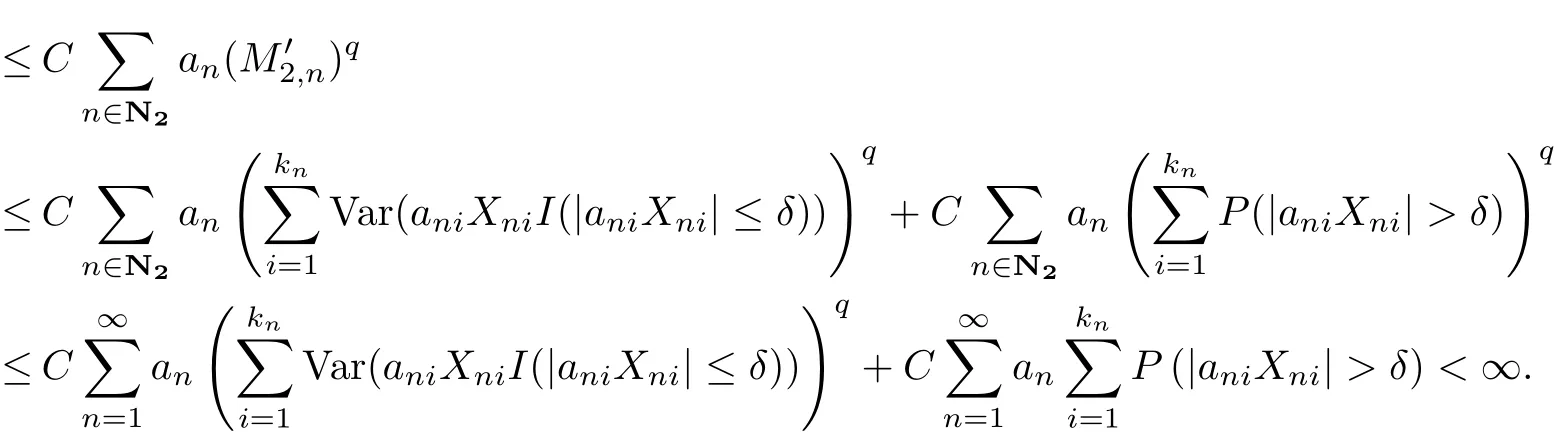
This completes the proof of the theorem.

By Theorem 3.1,we can get the following corollary immediately.The details are omitted.

Corollary 3.1Let{Xni,1≤i≤kn,n≥1}be an array of rowwise END random variables.Assume that{ani,1≤i≤kn,n≥1}is an array of real numbers and{an,n≥1}is a sequence of positive constants.If conditions(3.1)and(3.2)of Theorem 3.1 satisfy and

Then

The following corollary is an application of Corollary 3.1.

Corollary 3.2Let{Xni,1≤i≤kn,n≥1}be an array of rowwise END random variables with EXni=0,for all 1≤i≤kn,n≥1.Assume that{ani,1≤i≤kn,n≥1}is an array of real numbers and{an,n≥1}be a sequence of positive constants.Let Φ(x)be a real function such that for some δ＞0,

Suppose that for all ε＞0,(3.1)satisf i es and there exists some q≥1,such that

and

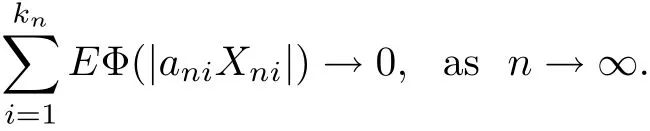
Then

ProofWe will check the conditions of Corollary 3.1 are satisf i ed.It is easily seen that

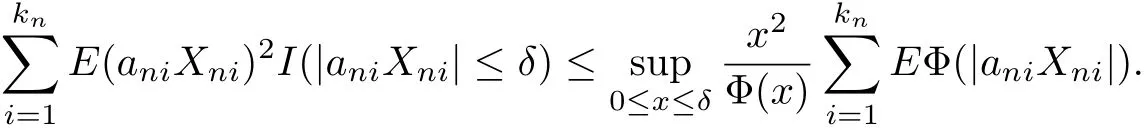
Since EXni=0,it follows that

which implies that

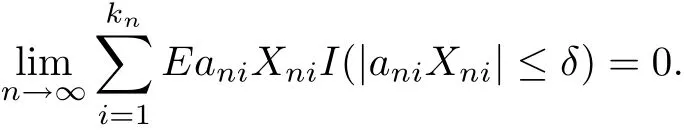
The desired result follows from Corollary 3.1 immediately.The proof is complete.

With the Theorem 3.1 accounted for,we can get the following result for arrays of rowwise END random variables with mean zero.

Theorem 3.2Let{Xni,1≤i≤kn,n≥1}be an array of rowwise END random variables with EXni=0.Assume that{ani,1≤i≤kn,n≥1}is an array of real numbers and {an,n≥1}be a sequence of positive constants.Assume that for any ε＞0 and some δ＞0,

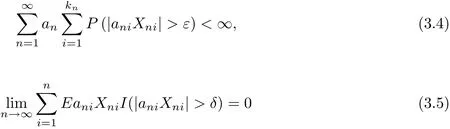
and there exist q≥1 and 0＜t≤2 such that

Then

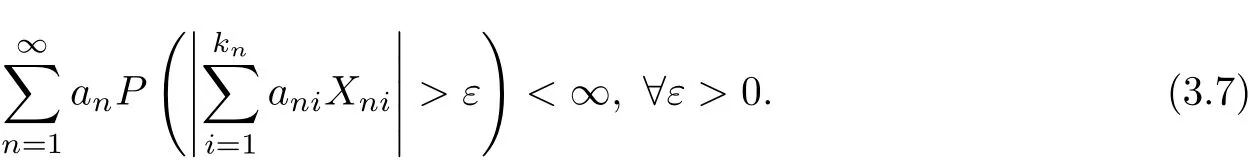
ProofIt suffices to prove that condition(3.2)of Theorem 3.1 is satisf i ed.Let 0＜t≤2, we have

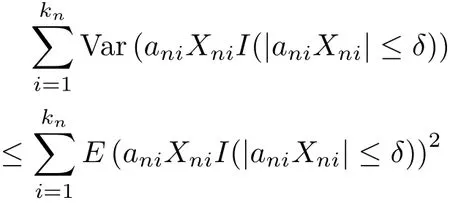
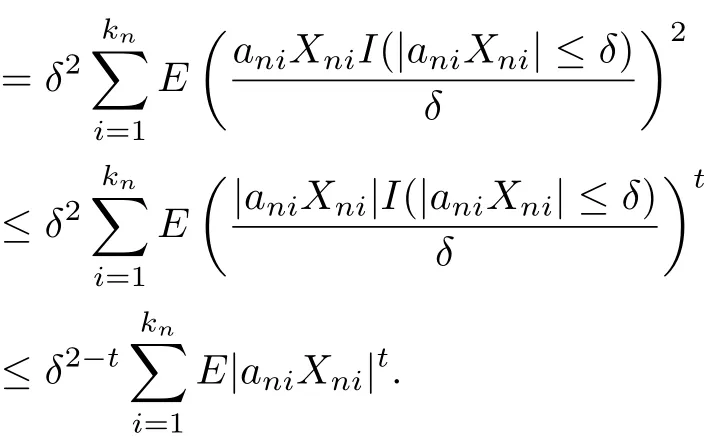
Then

By condition(3.5),for any f i xed ε＞0 and n large enough,

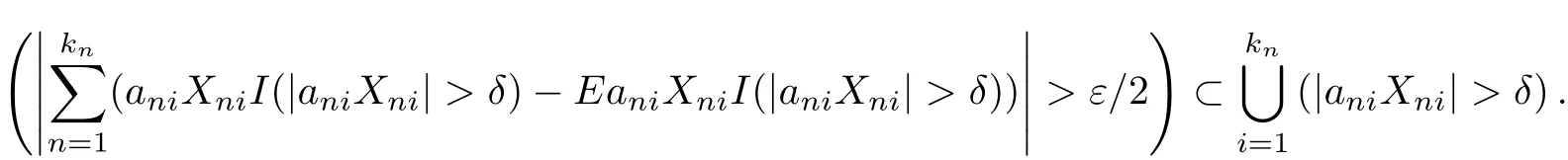
Therefore,by EXni=0,we have for n large enough that

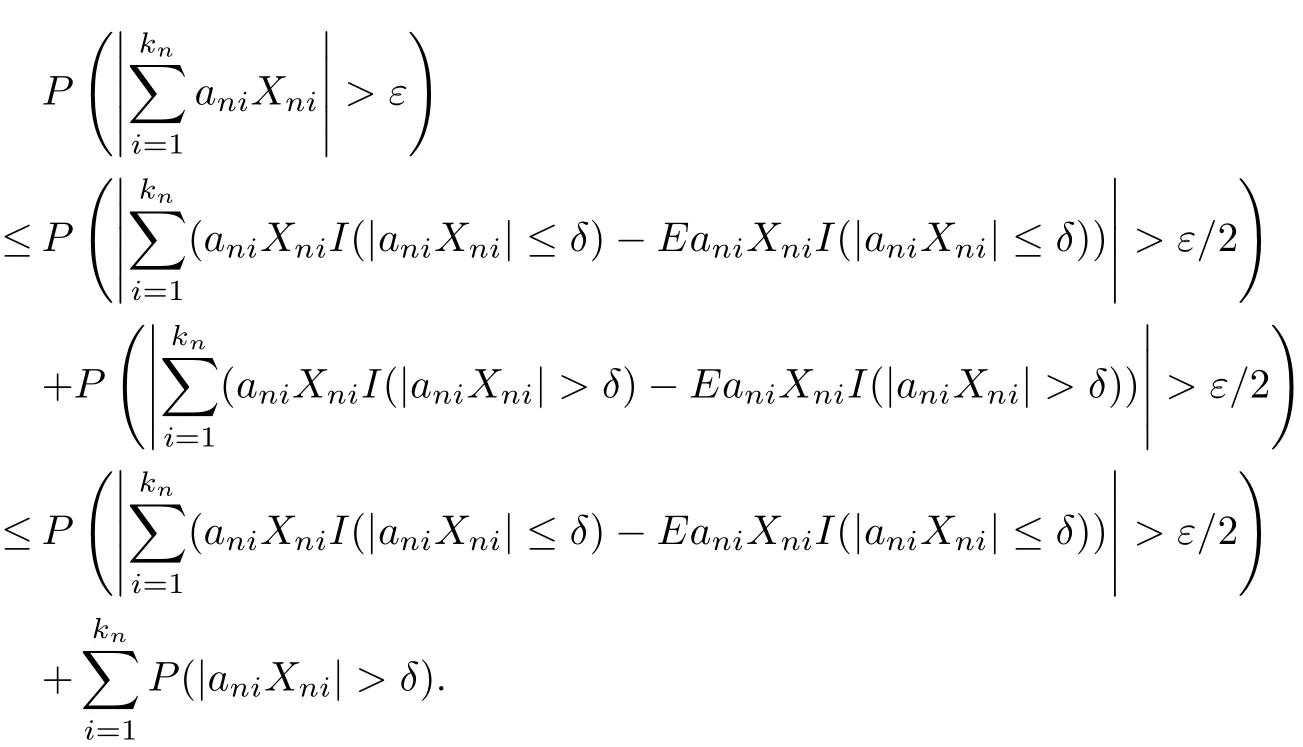
By the same argument as in the proof of Theorem 3.1,the proof of the Theorem 3.2 is completed.

AcknowledgementThe authors are most grateful to the editor and anonymous referees for careful reading of the manuscript and valuable suggestions which helped in signif i cantly improving an earlier version of this paper.

[1]HSU P,ROBBINS H.Complete convergence and the law of large numbers[J].Proceeding of the National Academy of Science of the United States of America,1947,33(2):25-31.

[2]ERD¨OS P.On a theorem of Hsu and Robbins[J].The Annals of Mathematical Statistics,1949,20:286-291.

[3]GUT A.On complete convergence in the law of large numbers for subsequences[J].Annals of Probability, 1985,13(4):1286-1291.

[4]HU T C,SZYNAL D,VOLODIN A.A note on complete convergence for arrays[J].Statistics and Probability Letters,1998,38(1):27-31.

[5]HU T C,VOLODIN A.A note on complete convergence for arrays[J].Statistics and Probability Letters, 2000,47(2):209-211.

[6]CHEN Ping-yan,HU T C,LIU Xiang-dong,et al.On complete convergence for arrays of rowwise negatively associated random variables[J].Theory of Probability and Its Applications,2008,52:323-328.

[7]SUNG S H.Complete convergence for weighted sums of random variables[J].Statistics and Probability Letters,2007,77(3):303-311.

[8]SUNG S H.A note on the complete convergence for arrays of rowwise independent random elements[J]. Statistics and Probability Letters,2008,78(11):1283-1289.

[9]WANG Xue-jun,HU Shu-he,YANG Wen-zhi.Complete convergence for arrays of rowwise negatively orthant dependent random variables[J].RACSAM,2012,106:235-245.

[10]ZHOU Xin-cai,TAN Chang-chun,LIN Jin-guan.On the strong laws for weighted sums of ρ∗-mixing random variables[J].Journal of Inequalities and Applications,2011,2011(1):1-8.

[11]WU Qun-ying.A strong limit theorem for weighted sums of sequences of negatively dependent random variables[J].Journal of Inequalities and Applications,2010,2010(1):1-8.

[12]WU Qun-ying.Sufficient and necessary conditions of complete convergence for weighted sums of PNQD random variables[J].Journal of Applied Mathematics,2012,2012(1):1-10.

[13]WU Qun-ying.A complete convergence theorem for weighted sums of arrays of rowwise negatively dependent random variables[J].Journal of Inequalities and Applications,2012,2012(1):1-10.

[14]SHEN Ai-ting.On strong convergence for weighted sums of a class of random variables[J].Abstract and Applied Analysis,2013,Volume 2013,2013(1):1-7.

[15]SHEN Ai-ting,WU Ran-chao.Strong convergence for sequences of asymptotically almost negatively associated random variables[J].Stochastics:An International Journal of Probability and Stochastic Processes, 2014,86(2):291-303.

[16]QIU De-hua,CHANG K C,ANTONINI R G,et al.On the strong rates of convergence for arrays of rowwise negatively dependent random variables[J].Stochastic Analysis and Application,2011,29:375-385.

[17]LIU Li.Precise large deviations for dependent random variables with heavy tails[J].Statistics and Probability Letters,2009,79(9):1290-1298.

[18]LEHMANN E.Some concepts of dependence[J].The Annals of Mathematical Statistic,1966,37:1137-1153.

[19]JOAV-DEV K.,PROSCHAN F.Negative association of random variables with applications[J].The Annals of Statistic,1983,11:286-295.

[20]LIU Li.Necessary and sufficient conditions for moderate deviations of dependent random variables with heavyitails[J].Science in China Series A:Mathematics,2010,53(6):1421-1434.

[21]SHEN Ai-ting.Probability inequalities for END sequence and their applications[J].Journal of Inequalities and Applications,2011,2011(1):1-12.

[22]WANG Shi-jie,WANG Wen-sheng.Extended precise large deviations of random sums in the presence of END structure and consistent variation[J].Journal of Applied Mathematics,2012,2012(1):1-12.

tion:60F15

1002–0462(2014)04–0592–10

date:2013-04-21

Supported by the National Natural Science Foundation of China(11201001);Supported by the Natural Science Foundation of Anhui Province(1208085QA03,1308085QA03);Supported by the Research Teaching Model Curriculum of Anhui University(xjyjkc1407);Supported by the Students Science Research Training Program of Anhui University(KYXL2014017)

Biographies:ZHENG Lu-lu(1989-),female,native of Hefei,Anhui,M.S.D.,engages in probability limit theorem;WANG Xue-jun(1981-),male,native of Hefei,Anhui,an associate professor of Anhui Universiry, Ph.D.,engages in probability limit theorem.

CLC number:O211.4Document code:A