On Laguerre Isopararmetric Hypersurfaces in ℝ7

JI Xiu,HU Chuan-feng

(College of Arts and Science,Yangtze University,Jingzhou 434000,China)

On Laguerre Isopararmetric Hypersurfaces in ℝ7

JI Xiu,HU Chuan-feng

(College of Arts and Science,Yangtze University,Jingzhou 434000,China)

Let x:M→ℝnbe an umbilical free hypersurface with non-zero principal curvatures,then x is associated with a Laguerre metric g,a Laguerre tensor L,a Laguerre form C,a Laguerre second fundamental form B,which are invariants of x under Laguerre transformation group.A classical theorem of Laguerre geometry states that M(n＞3)is characterized by g and B up to Laguerre equivalence.A Laguerre isopararmetric hypersurface is def i ned by satisfying the conditions that C=0 and all the eigenvalues of B with respect to g are constant.It is easy to see that all Laguerre isopararmetric hypersurfaces are Dupin hypersurfaces.In this paper,we established a complete classif i cation for all Laguerre isopararmetric hypersurfaces with three distinct principal curvatures in ℝ7.

laguerre metric;laguerre form;laguerre tensor;laguerre second fundamental form;laguerre isopararmetric hypersurface

§1.Introduction

Let Uℝnbe the unit tangent bundle over ℝn.An oriented sphere in ℝncentered at p with radius r can be regarded as the“oriented sphere”{(x,ξ)|x−p=rξ}in Uℝn,where x is the position vector and ξ the unit normal of the sphere.An oriented hyperplane in ℝnwith constant unit normal ξ and constant real number c can be regarded as the”oriented hyperplane”{(x,ξ)|x·ξ=c}in Uℝn.A dif f eomorphism ψ:Uℝn→Uℝnwhich takes oriented spheres to oriented spheres,oriented hyperplanes to oriented hyperplanes,preserving the tangentialdistance of any two spheres,is called a Laguerre transformation.All Laguerre transformations in Uℝnform a group called Laguerre transformation group.

An oriented hypersurface x:M→ℝncan be identif i ed as the submanifold(x,ξ):M→Uℝn,where ξ is the unit normal of x.Two hypersurfaces x,x′:M→ℝnare called Laguerre equivalent,if there is a Laguerre transformation ψ:Uℝn→Uℝnsuch that(x′,ξ′)=ψ◦(x,ξ). In Laguerre geometry one studies properties and invariants of hypersurfaces in ℝnunder the Laguerre transformation group.

Laguerre geometry of surfaces in ℝ3has been developed by Blaschke and his schools[1]. Further discussions in this direction have been carried out by many other authors[25].

In[6],Li and Wang have studied Laguerre dif f erential geometry of oriented hypersurfaces inℝn.For any umbilical-free hypersurface x:M→ℝnwith non-zero principal curvatures,they def i ned a Laguerre invariant metric g,a Laguerre tensor L,a Laguerre form C and a Laguerre second fundamental form B on M,and showed that{g,B}is a complete Laguerre invariant system for hypersurfaces in ℝnwith n＞3.In the case n=3,a complete Laguerre invariant system for surfaces in ℝ3is given by{g,B,L}.

An important class of hypersurfaces for Laguerre dif f erential geometry is the so-called Laguerre isopararmetric hypersurfaces in ℝn.Recall that,according to[7],by a Laguerre isopararmetric hypersurface in ℝn,we mean that it is an umbilical free hypersurface with non-zero principal curvature of ℝnsuch that Laguerre form vanishes and all Laguerre principal curvatures are constant.Note that,by Laguerre principal curvatures,we mean the so-called eigenvalues of B with respect to g.In[7],Li and Sun classif i ed all Laguerre isopararmetric hypersurfaces inℝ4.Recently,we have classif i ed all Laguerre isopararmetric hypersurfaces in ℝ5and ℝ6.Here, we will classify all Laguerre isopararmetric hypersurfaces in ℝ7with three distinct principal curvatures.In order to obtain our result,we will use the following theorems.

Theorem 1.1[8]Let x:Mn−1→ℝnbe an umbilical free hypersurface with non-zero principal curvatures.If its Laguerre second fundamental form is parallel,then x is Laguerre equivalent to an open part of one of the following hypersurfaces.

(1)The oriented hypersurface x:Sk−1×ℍn−k→ℝnwill be given by the following Example 1;

(2)The image of τ of the oriented hypersurface x:ℝn−1→ℝn0will be given by the following Example 2.

Theorem 1.2[9]Let x:Mn−1→ℝnbe an umbilical free hypersurface with non-zero principal curvatures,where x has constant Laguerre eigenvalues.If Laguerre form of x is vanishing and x is not a Laguerre isotropic hypersurface,then x is Laguerre equivalent to an open part of one of the following hypersurfaces.

(1)The oriented hypersurface x:Sk−1×ℍn−k→ℝnwill be given by the following Example 1;

(2)The oriented hypersurface will be given by the following Example 3.

Example 1For any integer k with 1≤k≤n−1 we denote by ℍn−k={(v,w)∈|υ·υ−ω2=−1,ω＞0}the hyperbolic space embedded in the Minkowski spaceand Sk−1the k−1-dimensional unit sphere in ℝk.We de fi ne x:Sk−1×ℍn−k→ℝnby

In[8],the authors have proved that the Laguerre second fundamental form of x is parallel, and x is a Laguerre isopararmetric hypersurface with two distinct Laguerre principal curvatures.

Before giving the second example,we have to describe the Laguerre embedding τ:→Uℝn(for details we refer to[6]).Letbe the Minkowski space with inner product

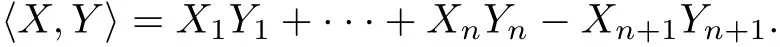
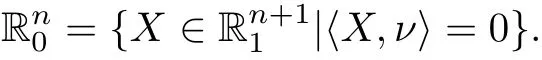
We def i ne

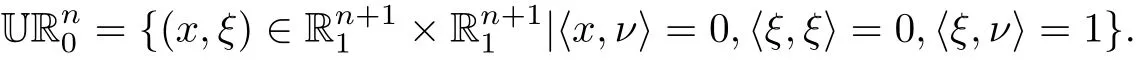
And we def i ne τ:Uℝn0→Uℝnby

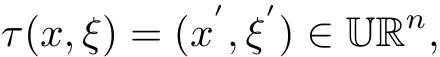
where x=(x1,x0,x1)∈ℝ×ℝn−1×ℝ,ξ=(ξ1+1,ξ0,ξ1)∈ℝ×ℝn−1×ℝ and

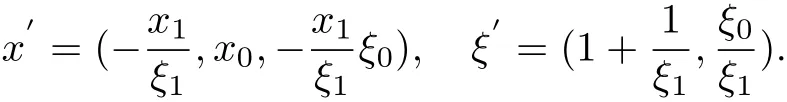
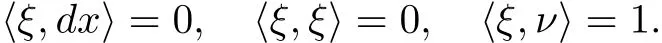
From τ(x,ξ)=(x′,ξ′)∈Uℝn,we get a hypersurface x′:M→ℝn.

Example 2For any positive integers m1,···,mswith m1+···+ms=n−1 and any non-zero constants λ1,···,λs,we def i ne x:ℝn−1→ℝn0,a space-like oriented hypersurface inℝn0by

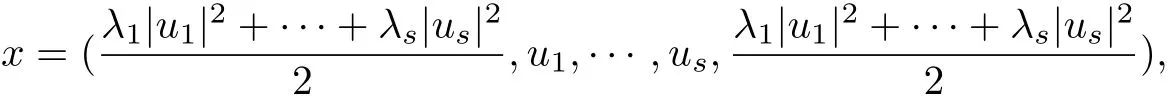
where(u1,···,us)∈ℝm1×···×ℝms=ℝn−1and|ui|2=ui·ui,i=1,···,s.Then τ◦(x,ξ)= (x′,ξ′):ℝn−1→ℝn0and we get the hypersurface x′:ℝn−1→ℝn.

In[8],the authors have proved that the Laguerre second fundamental form of x is parallel, and x is a Laguerre isopararmetric hypersurface with s distinct Laguerre principal curvatures.

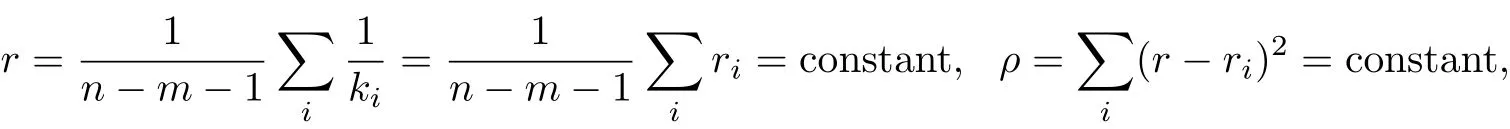
where kiare the principal curvatures of y.

Let f:Sm(1)→ℝm+1be the canonical embedding where Sm(1)is a m-dimensional unit sphere.Locally we can def i ne hypersurface in ℝnas follows,

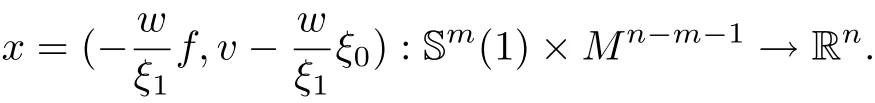
In[8],the authors have proved that x has constant Laguerre eigenvalues and vanishing Laguerre form,and x is a Laguerre isopararmetric hypersurface with two distinct Laguerre principal curvatures.

Our main objective here is to prove the following main theorem.

Theorem 1.3(Main Theorem)Let x:M6→ℝ7be an umbilical free hypersurface with non-zero principal curvatures.If x is Laguerre isopararmetric hypersurfaces with three distinct Laguerre principal curvatures,then x is Laguerre equivalent to the image of τ of the oriented hypersurface x:ℝ6→ℝ70given by Example 2 with s=3.

The organization of this paper is as follows.In section 2,we review some elementary facts of Laguerre geometry for hypersurfaces in ℝn.In section 3,by investigating Laguerre isoparametric hypersurfaces in ℝ7with three distinct Laguerre principal curvatures and▽B/=0, we prove that there are no such Laguerre isopararmetric hypersurfaces(Theorem 3.1).Finally, in section 4,we complete the proof of the Main Theorem.

§2.Laguerre Geometry of Hypersurfaces in ℝn

In this section,we review Laguerre invariants and structure equations of hypersurfaces inℝn.For more details we refer to[6].

Let ℝn+3

新课程改革要求课堂的教学形式要多样化、活动化、开放化，提倡将一些生动有趣的教学形式引入课堂。因此，打造学生的幸福课堂，必须丰富我们的课堂教学形式。

2be the space ℝn+3,equipped with the inner product

Let Cn+2be the light-cone in ℝn+3given by Cn+2={X∈ℝn2+3|〈X,X〉=0}.Denote by LG the subgroup of orthogonal group O(n+1,2)on ℝn2+3given by

where℘=(1,−1,0,0),0∈Rn,is a light-like vector in ℝn+32.

Let x:M→ℝnbe an umbilical free hypersurface with non-zero principal curvatures and ξ:M→Sn−1be its unit normal.Let{e1,···,en−1}be the orthonormal basis for TM withrespect to dx·dx,consisting of unit principal vectors.We write the structure equations of x:M→ℝnby

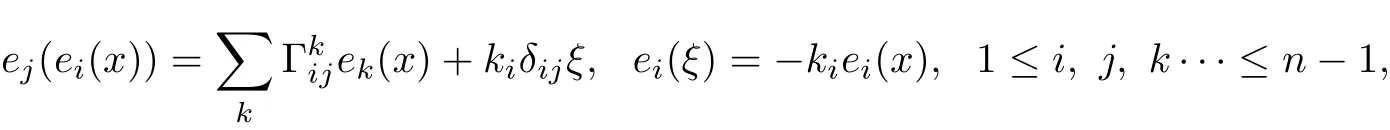
where ki/=0 is the principal curvature corresponding to ei.Let

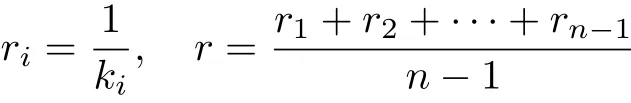
be the curvature radius and mean curvature radius of x respectively.We def i ne

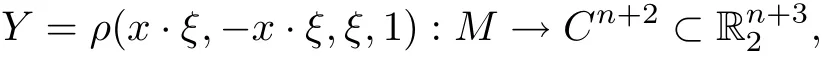
Theorem 2.1Let x,x˜:M→ℝnbe two umbilical free oriented hypersurfaces with non-zero principal curvatures.Then x andx˜ are Laguerre equivalent if and only if there exists T∈LG such thatY˜=Y T.

From this theorem we see that

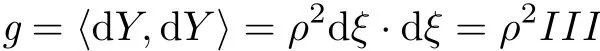
is a Laguerre invariant metric,where III is the third fundamental form of x.

Letting△be the Laplace operator of g,we def i ne

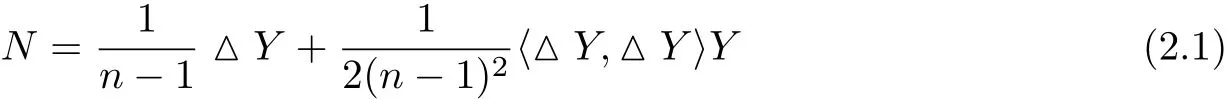
and

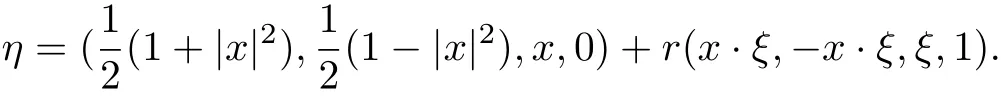
From(2.1)we get

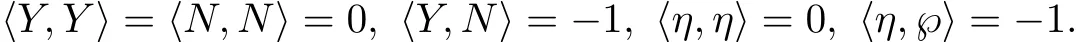
Let{E1,···,En−1}be an orthonormal basis for g=〈dY,dY〉with dual basis{w1,···,wn−1}. Then we have the following orthogonal decomposition

We call{Y,N,E1(Y),E2(Y),···,En−1(Y),η,℘}a Laguerre moving frame in ℝn+32of x.By taking derivatives of this frame,we obtain the following structure equations

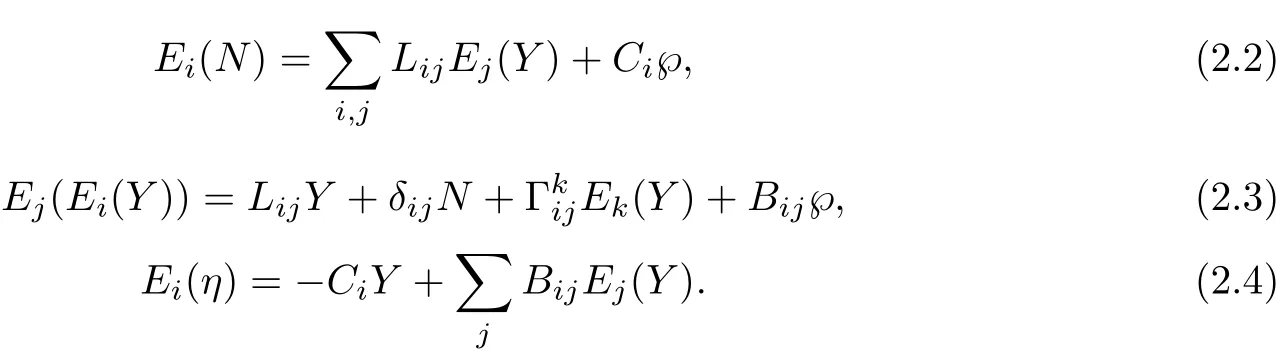
From these equations we obtain the following basic Laguerre invariants.

1)The Laguerre metric g=〈dY,dY〉;

2)The Laguerre second fundamental form

3)The Laguerre symmetric 2-tensor

The covariant derivative of Lij,Bijare def i ned by

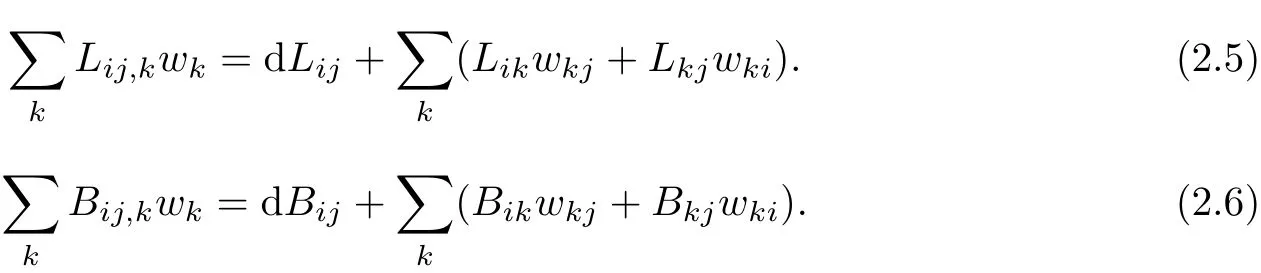
The second covariant derivative of Bijare def i ned by

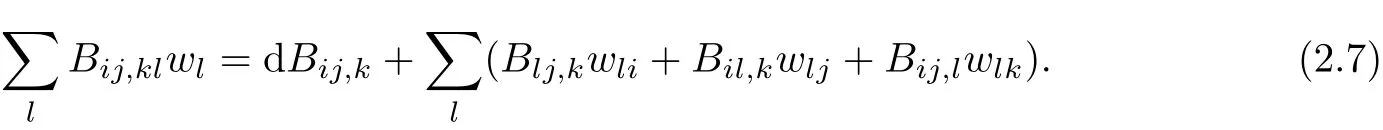
By exterior dif f erentiation of(2.6),we have the following Ricci identities

By taking further derivatives of(2.2)～(2.4),we get the following relations between these invariants

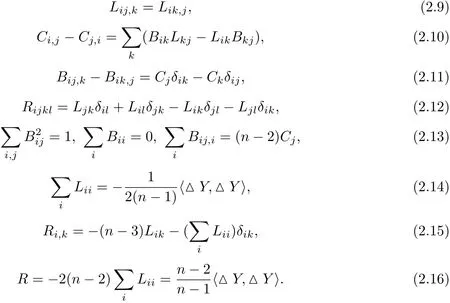
In the case n＞3,we know from(2.13)and(2.15)that Ciand Lijare completely determined by the Laguerre invariants{g,B}and thus we get

Theorem 2.2Two umbilical free oriented hypersurfaces in ℝn(n＞3)with non-zero principal curvatures are Laguerre equivalent if and only if they have the same Laguerre metric g and Laguerre second fundamental form B.

We def i ne˜Ei=riei,1≤i≤n−1,then{˜E1,···,˜En−1}is an orthonormal basis for III=dξ·dξ.Then{Ei=ρ−1˜Ei|1≤i≤n−1}is an orthonormal basis for the Laguerre metric g and we write{w1,···,wn−1}for its dual basis.By a direct calculation,we have

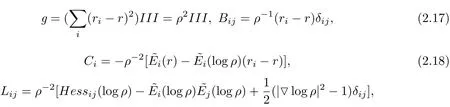
where,(Hessij)and▽are Hessian matrix and the gradient with respect to the third fundamental form III=dξ·dξ of the hypersurface x.

§3.Laguerre Isoparametric Hypersurfaces with Three Distinct Laguerre Principal Curvatures

In this section,we consider the case that x:M6→ℝ7is a Laguerre isoparametric hypersurface with three distinct Laguerre principal curvatures.If▽B≡0,we can use Theorem 1.1 directly;Now,we only consider the case that▽B/=0.Since the Laguerre form C vanishes,we can choose an orthonormal basis{Ei|1≤i≤6}with respect to Laguerre metric g such that

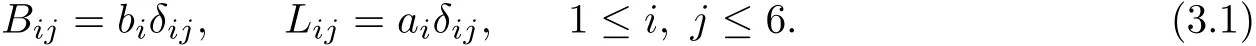
From(2.13)we have

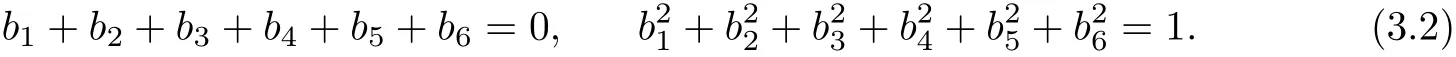
From(2.9),(2.11)and Laguerre form C=0,we see that both Lij,kand Bij,kare totally symmetric tensors.We def i ne

From(2.6),(3.1)and{bi}being constant,we get that for all i,j,k

3.1 Firstly,we consider the case that the multiplicities of principal curvatures are 2,2,2,respectively.

Now,we assume

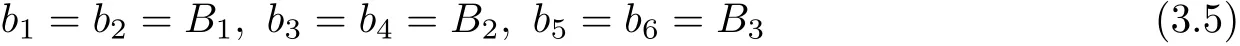
and B1,B2and B3are mutually distinct.From(3.4)we have for all i,j

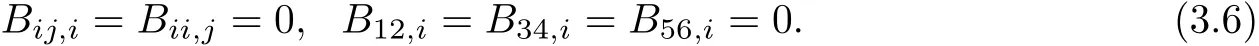
In this subsection,we use the following convention of indices

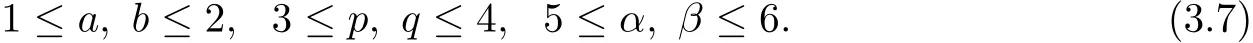
Lemma 3.1Bij,k/≡0,the following hold

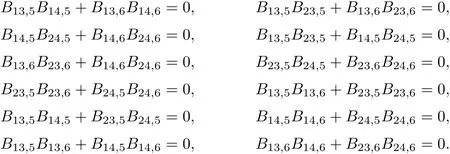
ProofFrom(2.7),(3.3)and(3.4),we have

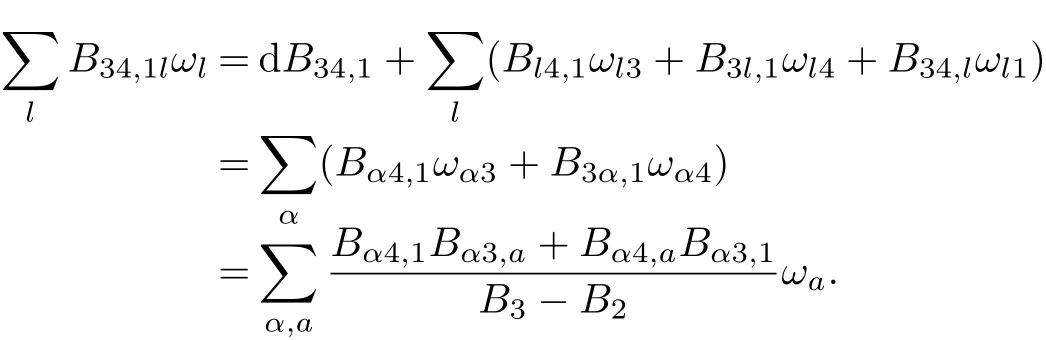
Therefore

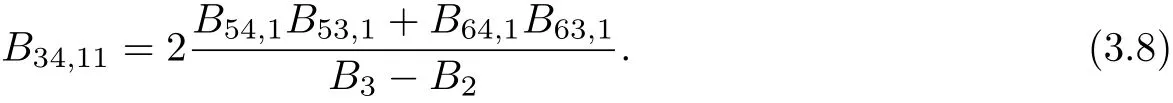
According to

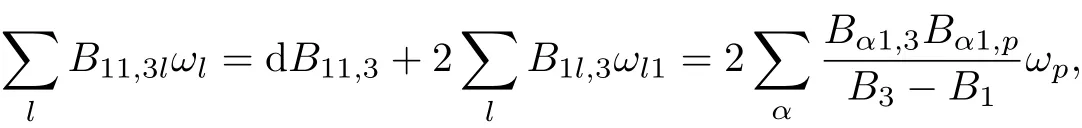
we can obtain

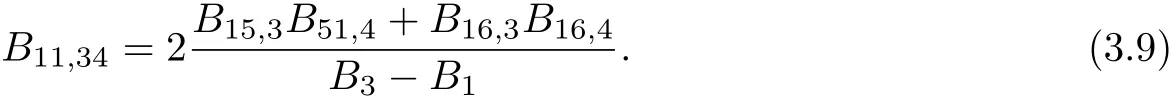
Using Ricci identity(2.8)and(3.1),we have

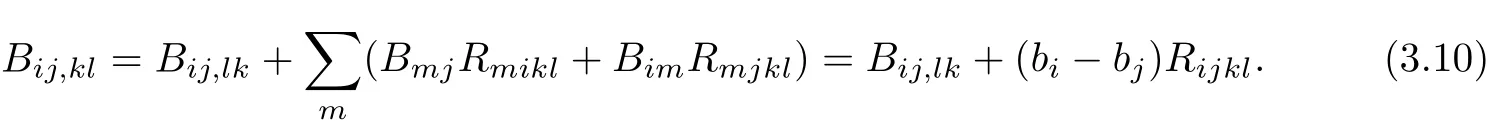
On the other hand,the Gauss equation(2.12)and(3.1)imply that

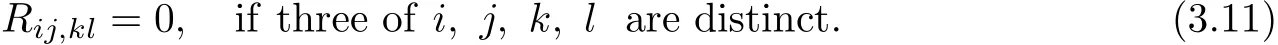
From(3.10)and(3.11),we get

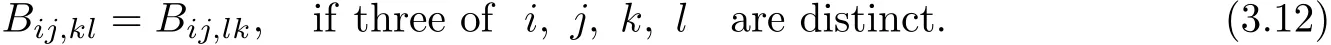
It follows from(3.12)that

Then,(3.8)～(3.9)and(3.13)give that B13,5B14,5+B13,6B14,6=0.Using the same way we can obtain the others.

Lemma 3.2Using Ricci identity,the following hold

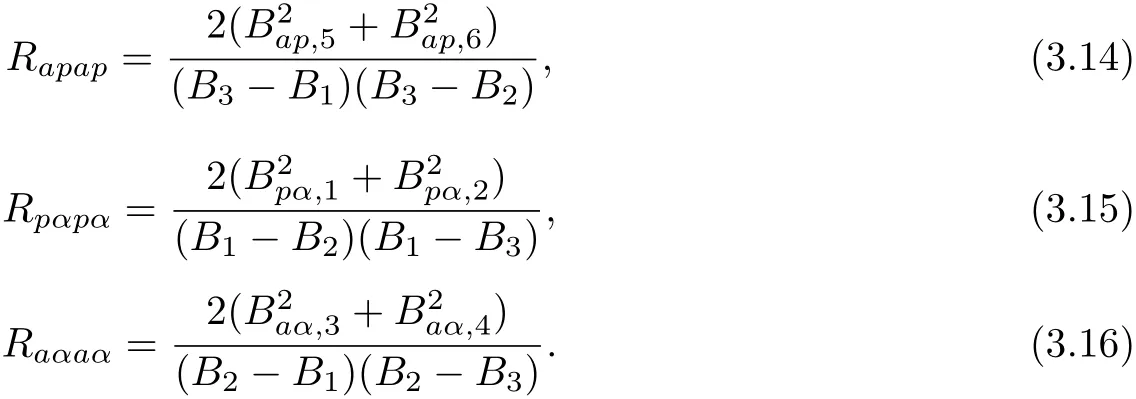
ProofFrom(2.7),(3.3)and(3.4),we have

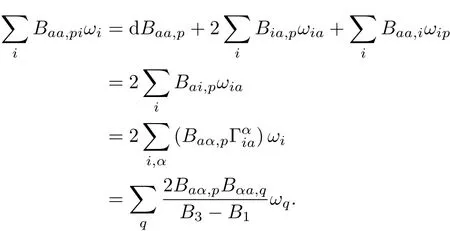
Hence

Analogously,we have

From(3.1)and(2.8),we obtain

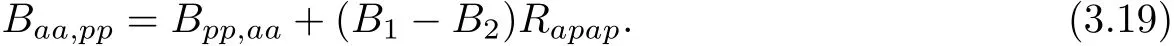
Then,(3.14)follows from(3.17)～(3.19).

From(3.6),we see that in{Bij,k}i≤j≤k,only eight elements,that is

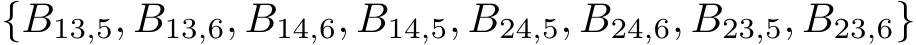
can be probably non-zero.Let α denote the number of non-zero elements in

According to Lemma 3.1,we know that α=1,2,3,4,8.

If α=1,without loss of generality we assume B13,5/=0,then we have one case:I-1;

If α=2 and B13,5/=0,by Lemma 3.1 B13,6=B14,5=B23,5=0,so one of{B14,6,B24,5, B24,6,B23,6}is non-zero,then we have four cases:I-2-I-5;

If α=3 and B13,5B14,6/=0,by Lemma 3.1 B13,6=B14,5=B23,5=B24,6=0,so one of{B24,5,B23,6}is non-zero,then we have two cases:I-6-I-7;If α=3 and B13,5B23,6/=0 or B13,5B24,5/=0,by Lemma 3.1 we have one case:I-(7)B24,5B13,5B23,6/=0.However,using the symmetry of indices 1 and 2 and the symmetry of indices 5 and 6,we easily see that I-(7)can be transformed into I-7.If B13,5B24,6/=0,by Lemma 3.1,we needn’t to consider;

If α=4 and B13,5B14,6B24,5/=0,by Lemma 3.1,we have one case:I-8;

In summary,we are sufficient to consider the following nine independent cases

I-1 B13,5/=0 and B13,6=B14,6=B14,5=B24,5=B24,6=B23,5=B23,6=0;

I-2 B13,5B14,6/=0 and B13,6=B14,6=B14,5=B24,5=B23,5=B23,6=0;

I-3 B13,5B23,6/=0 and B13,6=B24,6=B14,5=B24,5=B23,5=B23,6=0;

I-4 B13,5B24,5/=0 and B13,6=B14,6=B14,5=B24,5=B24,6=B23,5=0;

I-5 B13,5B24,6/=0 and B13,6=B14,6=B14,5=B24,6=B23,5=B23,6=0;

I-6 B13,5B14,6B24,5/=0 and B13,6=B14,5=B24,6=B23,5=B23,6=0;

I-7 B13,5B14,6B23,6/=0 and B13,6=B14,5=B24,5=B24,6=B23,5=0;

I-8 B13,5B14,6B23,6B24,5/=0 and B13,6=B14,5=B24,6=B23,5=0;

I-9 B13,5B13,6B14,6B14,5B24,5B24,6B23,5B23,6/=0.

Proposition 3.3Case I-1-I-9 do not occur.

Proof of Proposition 3.3

I-1B13,5/=0 and B13,6=B14,6=B14,5=B24,5=B24,6=B23,5=B23,6=0.

From Lemma 3.2,we have

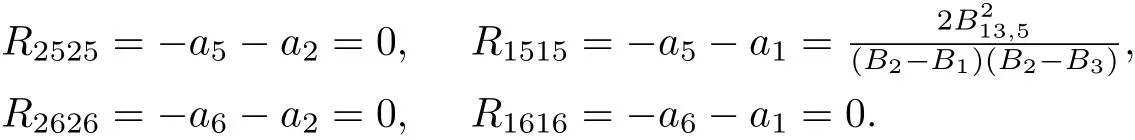
Since

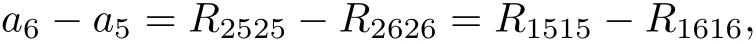
then,we get B13,5=0,a contradiction,so I-1 does not occur.Using the same way,we can obtain I-2～I-4 do not occur.

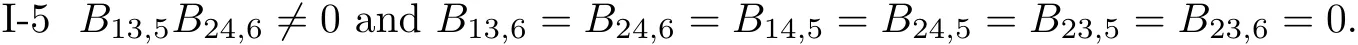
From Lemma 3.2,we have

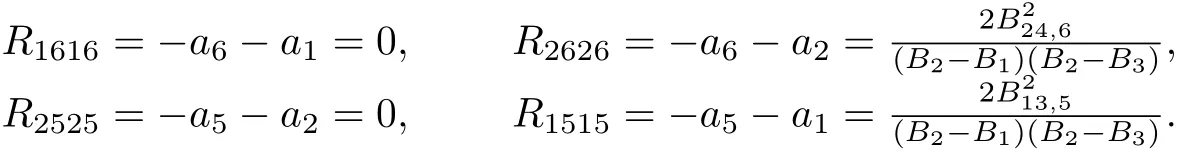
Since

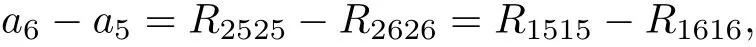
I-6 B13,5B14,6B24,5/=0 and B13,6=B14,5=B24,6=B23,5=B23,6=0.

From Lemma 3.2,we have

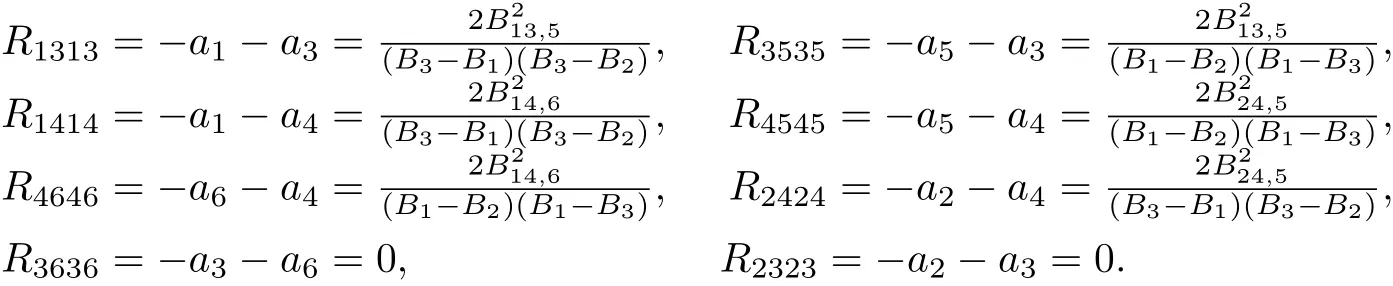
From

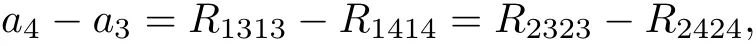
we have

From

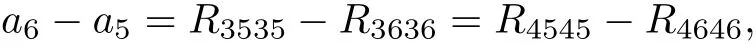
we get

Then(3.21)+(3.20)gives that B13,5=0,a contradiction,so I-6 does not occur.Using the same way,we can obtain I-7 does not occur.

I-8B13,5B14,6B24,5B23,6/=0 and B13,6=B14,5=B24,6=B23,5=0.

From Lemma 3.2,we have

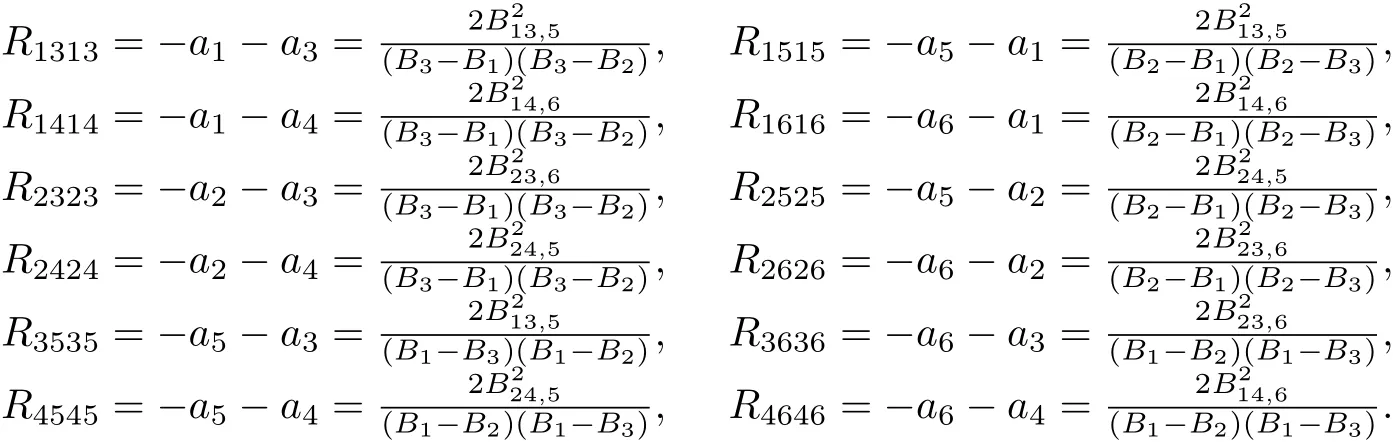
Since

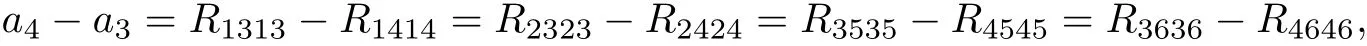
then,we have

From a5−a6=R1515−R1616=R2525−R2626,we get

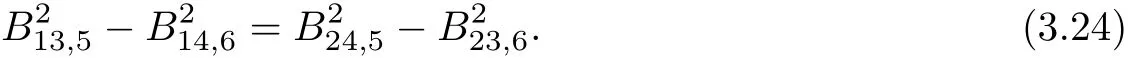
(3.22)+(3.23)gives that

(3.22)+(3.24)gives that

It follows from(3.25)and(3.26)that.Hence,we have R1313−R2323=a1−a2=0,R1313−R1414=a3−a4=0,R2525−R2626=a5−a6=0. Which imply that

Since

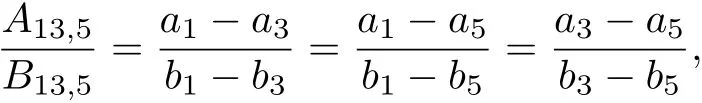
then,we have two functions λ andµso that a1+λb1=a3+λb3=a5+λb5=µ.

From(3.5),(3.27),we have

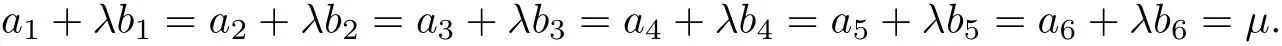
At the end of the paper,we can prove λ andµare constant.Thus,L has constant eigenvalues. If a6=a5=a4=a3=a2=a1,according to the above formulas,from R1313=R1515and R1313=R3535we have

Which implies that B1=B2,a contradiction.So x is not a Laguerre isotropic hypersurface. According to Theorem 1.2 and the hypersurfaces in Example 3 has only two distinct Laguerre principal curvatures,this produces the contradiction and therefore I-8 does not occur.

I-9 B13,5B13,6B14,6B14,5B24,5B24,6B23,5B23,6/=0.

Since

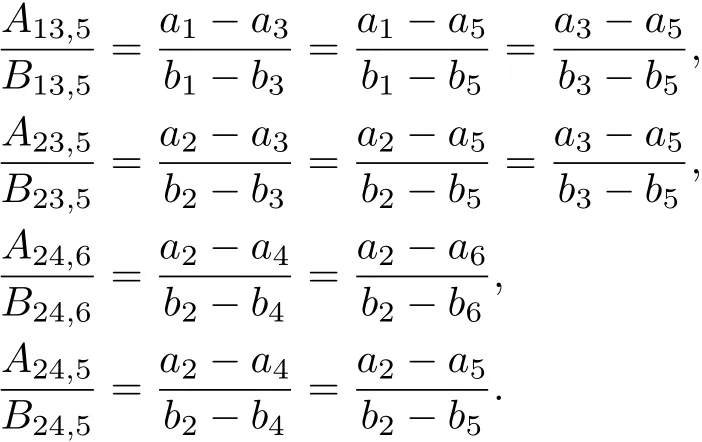
Then we have

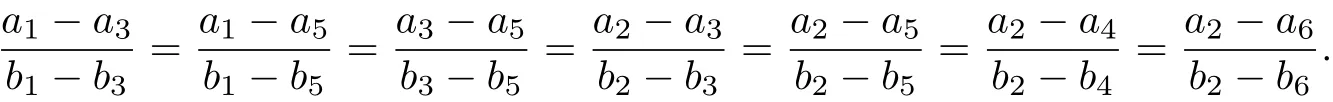
Hence,we have two functions λ andµso that

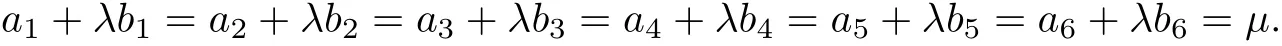
At the end of the paper,we can prove λ andµare constant.Thus,L has constant eigenvalues. From Lemma 3.2,we have

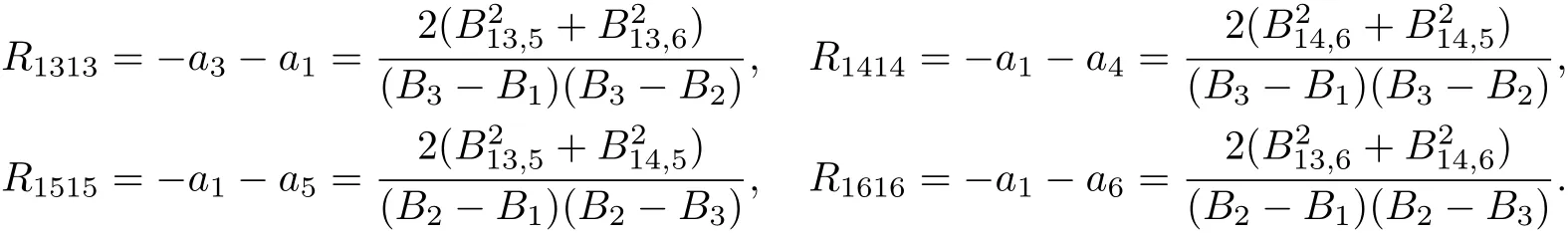
If a6=a5=a4=a3=a2=a1,from the above formulas,we have

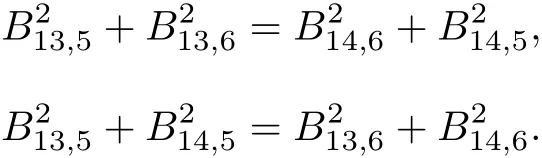
Analogously,we can obtain

It follows from(3.28)and(3.29)that B1=B2,a contradiction.So x is not a Laguerre isotropic hypersurface.According to Theorem 1.2 and the hypersurfaces in Example 3 has only two distinct Laguerre principal curvatures,this produces the contradiction and therefore I-9 does not occur.

3.2Now,we consider the case that the multiplicities of principal curvatures are 1,2,3,respectively.

We assume

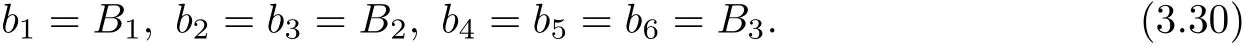
From(3.4),we have for all i,j

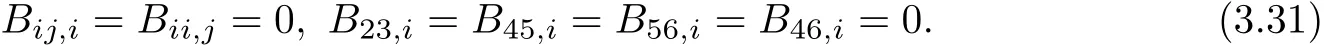
In this subsection,we use the following convention of indices

Lemma 3.4Bij,k/≡0,the following hold

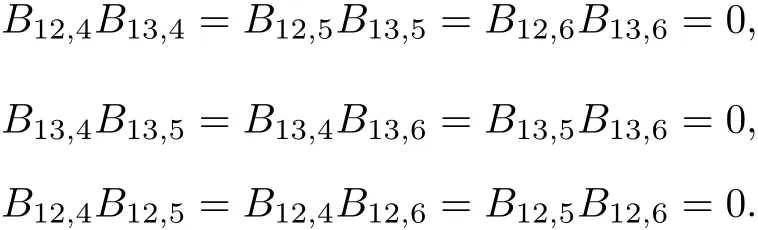
ProofFrom

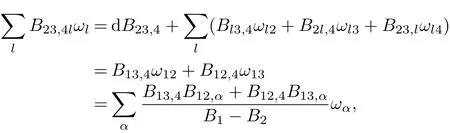
we get

According to

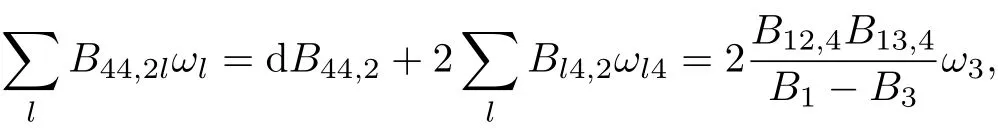
we can obtain

(3.12),(3.33)and(3.34)give that B12,4B13,4=0.using the same way we have the others.

Lemma 3.5Using Ricci identity,the following hold

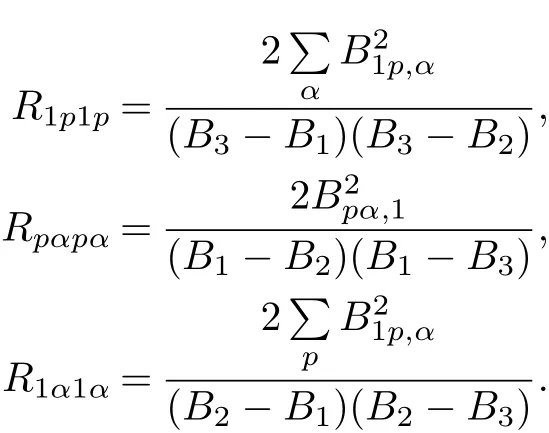
ProofUsing the similar proof of Lemma 3.2.

Since▽B/=0,according to Lemma 3.4,we know that at most one of{B12,4,B12,5,B12,6}or {B13,4,B13,5,B13,6}is nonzero.Hence,at most two of{B12,4,B12,5,B12,6,B13,4,B13,5,B13,6} are nonzero.According to Lemma 3.4,we may assume B12,4/=0 and B12,5=B12,6=B13,4= B13,5=B13,6=0,or B12,4B13,5/=0 and B12,5=B12,6=B13,4=B13,6=0,or B12,4B13,6/=0 and B12,5=B12,6=B13,4=B13,5=0,so we need consider the following three cases.

Case II-1B12,4/=0 and B12,5=B12,6=B13,4=B13,5=B13,6=0;

Case II-2B12,4B13,5/=0 and B12,5=B12,6=B13,4=B13,6=0;

Case II-3B12,4B13,6/=0 and B12,5=B12,6=B13,4=B13,5=0.

Proposition 3.6Case II-1～II-3 do not occur.

ProofII-1 B12,4/=0 and B12,5=B12,6=B13,4=B13,5=B13,6=0.

From Lemma 3.5,we have

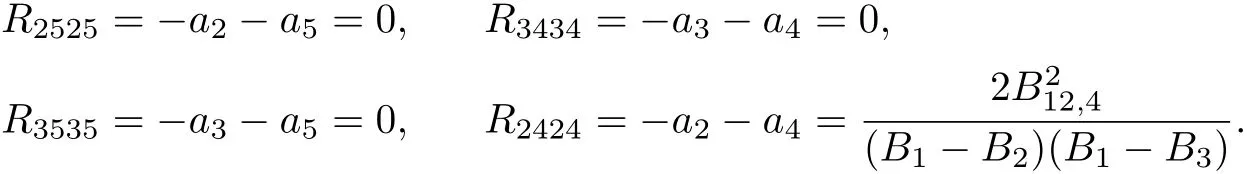
From

We obtain B12,4=0,a contradiction.So Case II-1 does not occur.Using the same way,we can obtain II-2 and II-3 do not occur.

As a combination of Proposition 3.3 and Proposition 3.6,we have

Theorem 3.1Let x:M6→ℝ7be an umbilical free hypersurface with non-zero principal curvatures.If x is Laguerre isopararmetric hypersurfaces with three distinct Laguerre principal curvatures,then▽B≡0.

ClaimLet x:Mn−1→ℝnbe an umbilical free hypersurface with non-zero principal curvatures which satisf i es(i)C=0(ii)L+λg+µB=0 for some functions λ andµ,then λ andµare constant.

ProofUsing the similar proof of[10].

§4.Proof of Theorem 1.3

Let x:M6→ℝ7be an umbilical free hypersurface with non-zero principal curvatures.If x is Laguerre isopararmetric hypersurfaces with three distinct Laguerre principal curvatures, then,by Theorem 3.1,Theorem 1.1,Example 1 and Example 2,we complete the proof of Theorem 1.3.

[1]BLASCHE W.Vorlesungen¨Uber Dif f erentialgeometrie[M].Berlin:Springer-Verlag,1929.

[2]LI Tong-zhu.Laguerre geometry of surfacs in ℝ3[J].Acta Mathematica Sinica,2005,21:1525-1534.

[3]MUSSO E,NICOLODI L.Laguerre geomery of surfaces with plane lines of curvature[J].Abh Math Sem Univ Hamburg,1999,69:123-138.

[4]MUSSO E,NICOLODI L.The Bianchi-Darboux transformation of L-isothermic surfaces[J].International Journal of Mathematics,2000,11:911-924.

[5]PALMER B.Remarks on a variation problem in Laguerre geometry[J].Rendiconti di Mathematica,Serie VII,1999,19:281-293.

[6]LI Tong-zhu,WANG Chang-ping.Laguerre geometry of hypersurfacs in ℝn[J].Manuscripta Math,2007, 122:73-95.

[7]LI Tong-zhu,SUN Hua-fei.Laguerre isopararmetric hypersurfaces in ℝ4[J].Acta Mathematica Sinica, English Series,2011,28:1179-1186.

[8]LI Tong-zhu,LI Hai-zhong,WANG Chang-ping.Classif i cation of hypersurfacs with parallel Laguerre second fundamental form in ℝn[J].Dif f erential Geom Appl,2010,28:148-157.

[9]LI Tong-zhu,LI Hai-zhong,WANG Chang-ping.Classif i cation of hypersurfacs with constant Laguerre eigenvalues in ℝn[J].Science China Mathematics,2011,54:1129-1144.

[10]LI Hai-zhong,WANG Chang-ping.Mobius geometry of hypersurfacs with constant mean curvature and constant scalar curvature[J].Manuscripta Math,2003,112:1-13.

tion:53A40,53B25

1002–0462(2014)04–0486–15

date:2012-10-15

Supported by the Department of Education of Hubei Province(B2014281)

Biographies:JI Xiu(1979-),female,native of Xinyang,Henan,a lecturer of Yangtze University,M.S.D., engages in global dif f erential geometry;HU Chuan-feng(1978-),male,native of Xinyang,Henan,a lecturer of Yangtze University,M.S.D.,engages in global dif f erential geometry and combinatorics and graph theory.

CLC number:O186.11Document code:A