A Kind of Identities for Products Reciprocals of q-binomial Coefficients

YANG Ji-zhen,WANG Yun-peng

(1.Department of Mathematics,Luoyang Normal College,Luoyang 471022,China;2.Department of Mathematics and Physical,Luoyang Institute of Science and Technology,Luoyang 471023,China)

A Kind of Identities for Products Reciprocals of q-binomial Coefficients

YANG Ji-zhen1,WANG Yun-peng2

(1.Department of Mathematics,Luoyang Normal College,Luoyang 471022,China;2.Department of Mathematics and Physical,Luoyang Institute of Science and Technology,Luoyang 471023,China)

The purpose of this paper is to establish some identities with products of q-Hermite polynomials,q-ultraspherical polynomials and reciprocals of q-binomial coefficients.

q-gamma function;q-beta function;q-integral;q-binomial coefficients

§1.Introduction

Let 0＜q＜1,q-gamma function Γq(x)is def i ned by

It is easy to see that

The generalized q-binomial coefficient is def i ned by

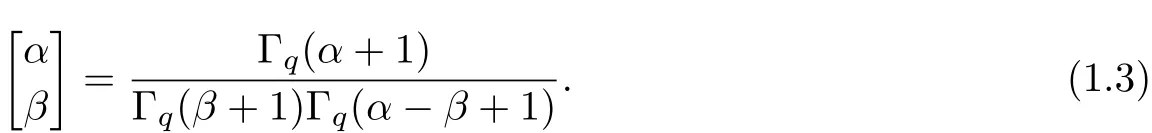
The q-Beta function is def i ned by

Thomae and Jackson introduced the q-intergral

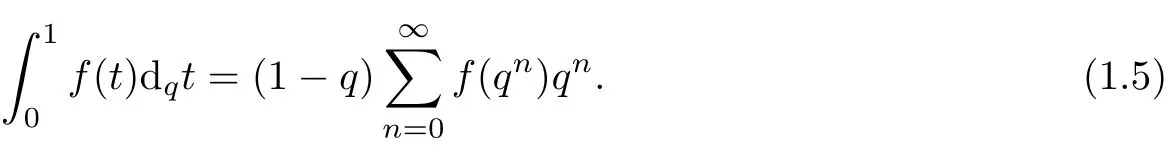
Then

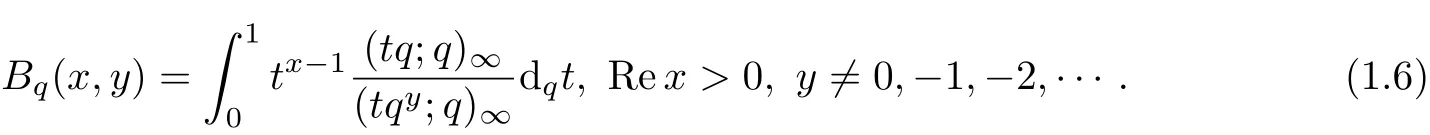
The details of above content,see[1,pages 20-24].

In[2-4],the integral representations and closed form representations for products reciprocals of binomial coefficients were discussed.The purpose of this paper is to get some identities with products of q-Hermite polynomials,q-ultraspherical polynomials and reciprocals of q-binomial coefficients.

§2.Main Results and Their Proofs

Theorem 1Let aibe real numbers with ai≥0,ji≥0(1≤i≤m)and|···＜1.Then

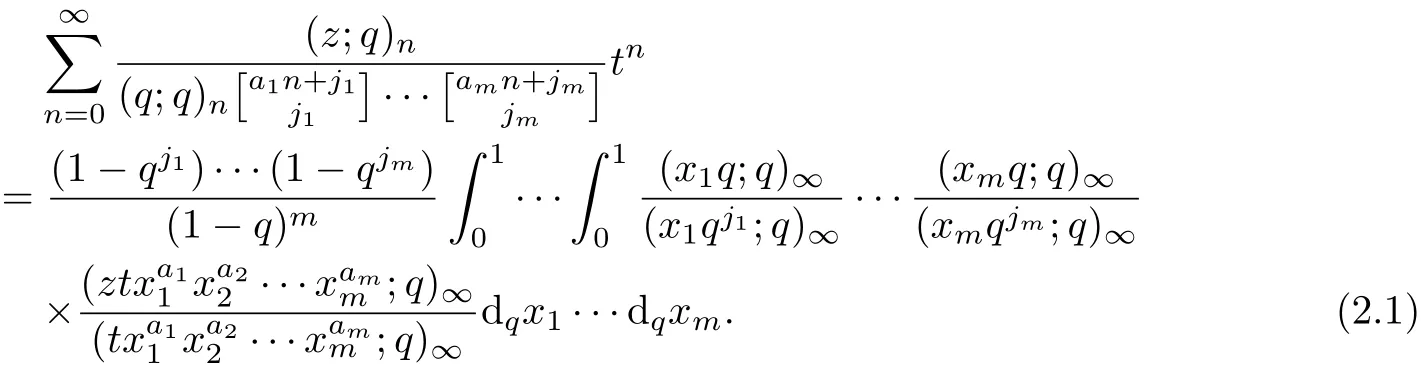
ProofApplying(1.1)～(1.6),we have

The proof of the theorem is completed.

If we take z→q and q→1 in Theorem 0.1,we can get the following identity. Corollary 1Let aibe real numbers with ai≥0,ji≥0(1≤i≤m)and|txa1

1···xamm|＜1.Then

Let m=1 in Corollary 1,we can get the following identity.

Corollary 2Let a be real numbers,j≥0 and|txa|＜1.Then

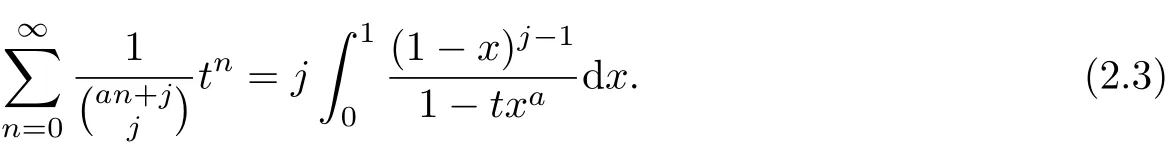
We can also obtain another result.

Theorem 2Let aibe real numbers with ai≥0,ji≥0(1≤i≤m)and|txa11···xamm|＜1. Then

ProofApplying(1.1)～(1.6),we have

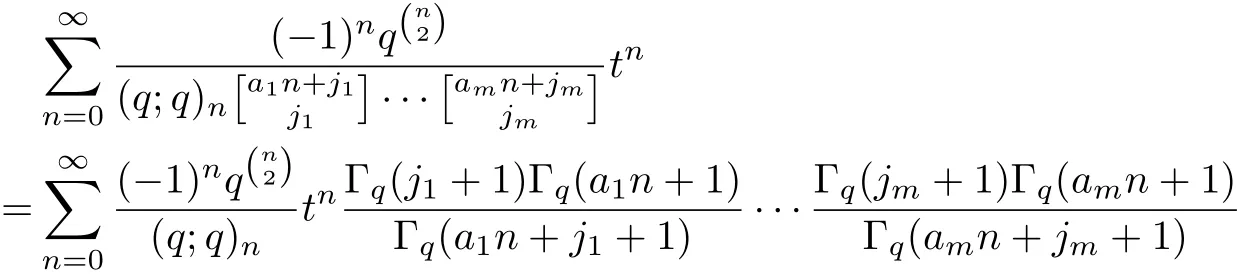
The proof of Theorem 2 is completed.

The continuous q-Hermite polynomials[1]are def i ned by

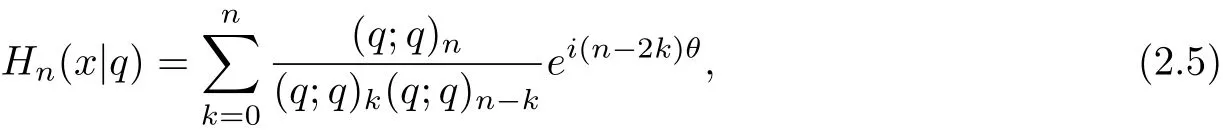
where x=cosθ.

By the excise 1.28 of[1]

We can obtain the following identity.

Theorem 3Let aibe real numbers with ai≥0,ji≥0(1≤i≤m)and|txa11···xamm|＜1. Then

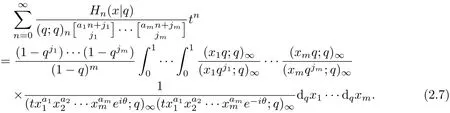
ProofBy equation(2.6),and using the same method in Theorem 1 and Theorem 2,we can get equation(2.7).

The continuous q-ultraspherical polynomials[1]are def i ned by

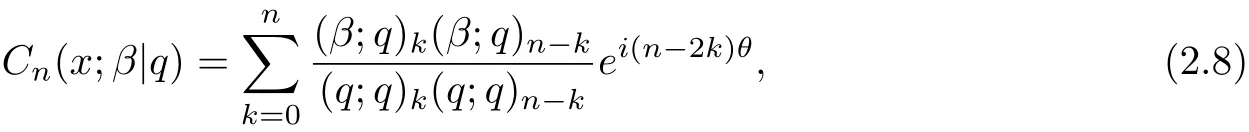
where x=cosθ.

By the excise 1.29 of[1]

and

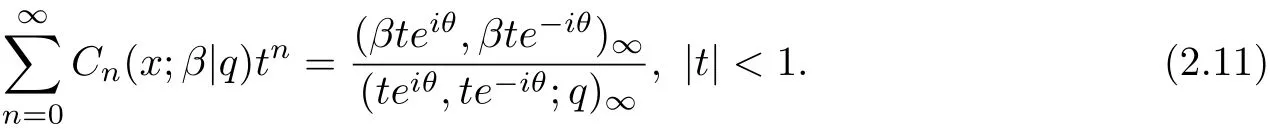
We can obtain the following identity.

Theorem 4Let aibe real numbers with ai≥0,ji≥0(1≤i≤m)and|txa11···xamm|＜1.Then

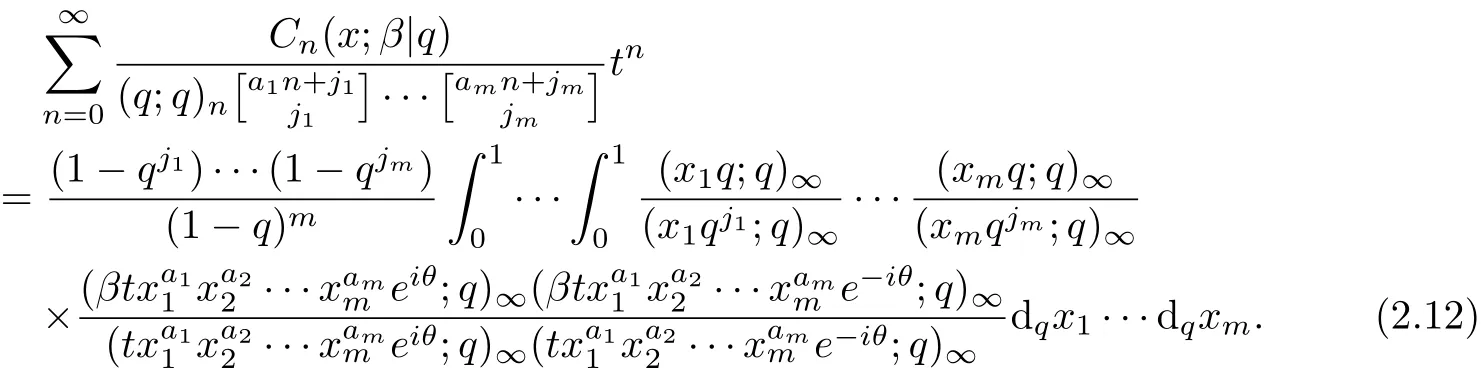
ProofSimilarly to Theorem 3,we can get the theorem.

§3.Summation Rormula Involving q-harmonic Numbers

The q-harmonic numbers are def i ned by

The generalization q-harmonic numbers can be def i ned by

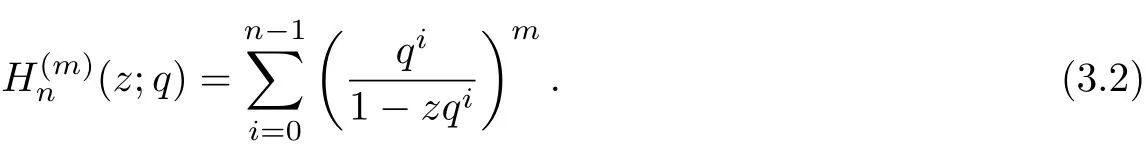
Observed that,let m=1 in the above identity,then

Dif f erentiating the identity of Theorem 1 with respect to the variable z,we can get the following identity.

Theorem 5Let aibe real numbers with ai≥0,ji≥0(1≤i≤m)and|txa1

1···xam

m|＜1.Then

ProofSince(z;q)n=(1−z)(1−zq)···(1−zqn−1),then

By the expansion of

Dif f erentiating the equation(3.5)with respect to the variable z,we have

Let N→∞in the above identity,we get

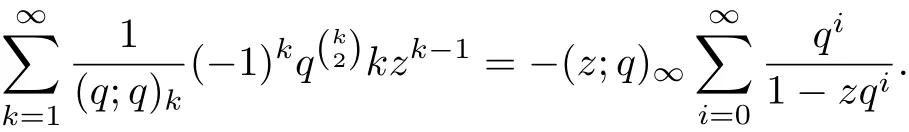
Applying the Euler expansion of

Then

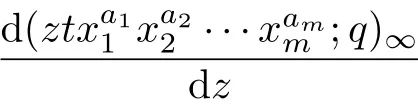
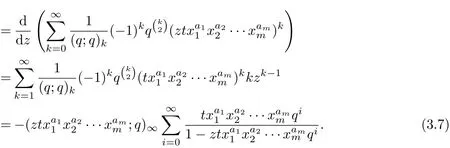
Dif f erentiating the equation(2.1)with respect to the variable z,then

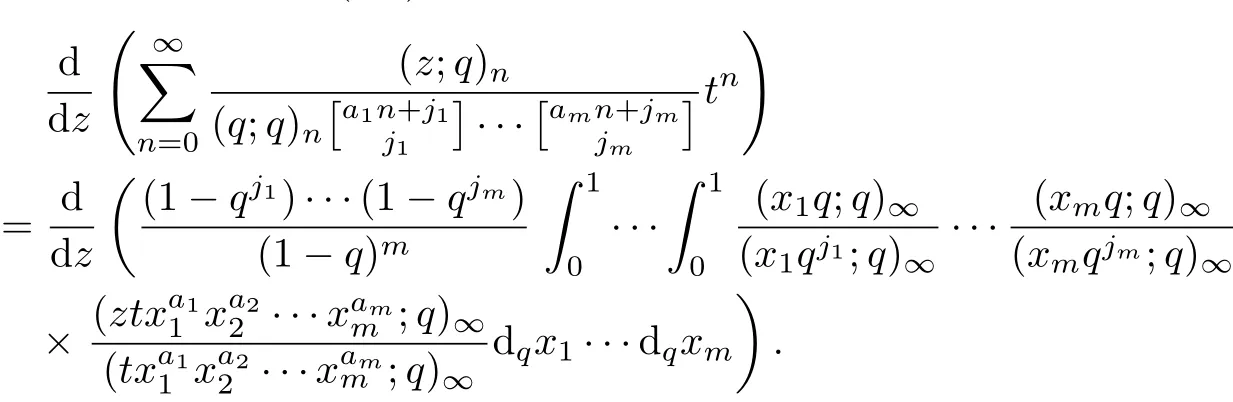
Using the identity(3.4)and(3.7),the result can be obtained.

Let m=2 in Theorem 5,then we can get the following identity.

Corollary 3Let aibe real numbers with ai≥0,ji≥0(1≤i≤2)and|t|＜1. Then

Dif f erentiating the identity of Theorem 1 with respect to the variable z twice,we can get the following identity.

Theorem 6Let aibe real numbers with ai≥0,ji≥0(1≤i≤m)and|txa1

1···xamm|＜1. Then

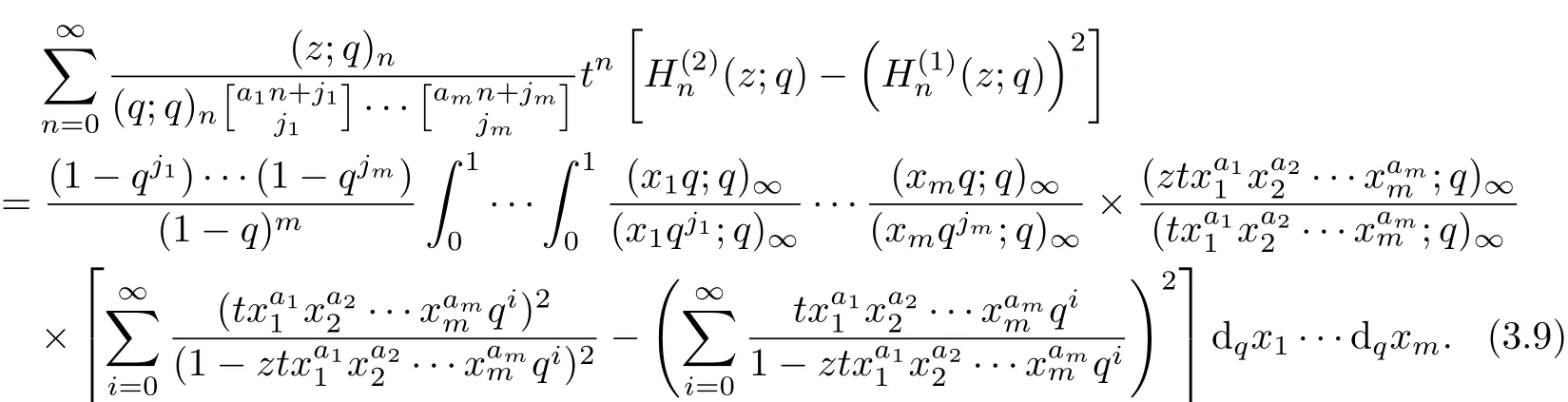
ProofDif f erentiating the equation(3.3)with respect to the variable z

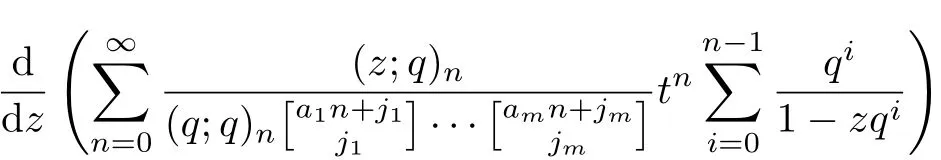
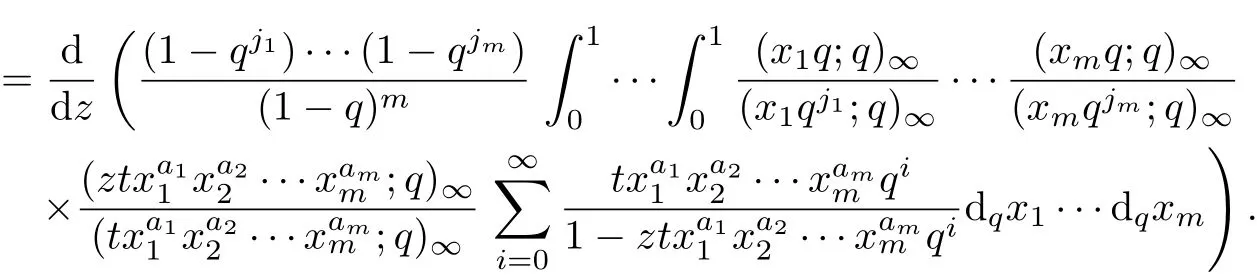
Since

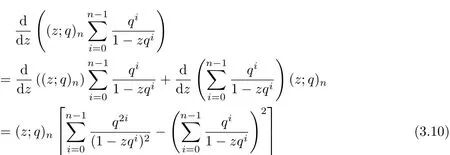
and

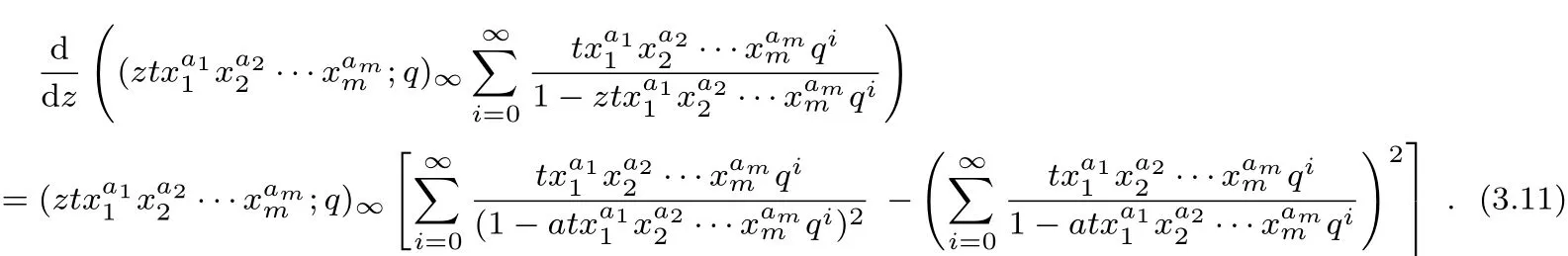
By equation(3.10)and(3.11),the result can be obtained.

Let m=2 in Theorem 0.6,we can get the following identity.

Corollary 4Let aibe real numbers with ai≥0,ji≥0(1≤i≤2)and|tx|＜1. Then

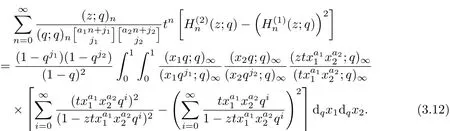
Dif f erentiating the identity of Theorem 1 with respect to the variable z for three times,the following identity can be deduced.

Theorem 7Let aibe real numbers with ai≥0,ji≥0(1≤i≤m)and|txa1

1···xam

m|＜1.Then

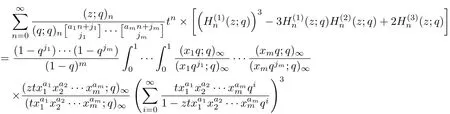
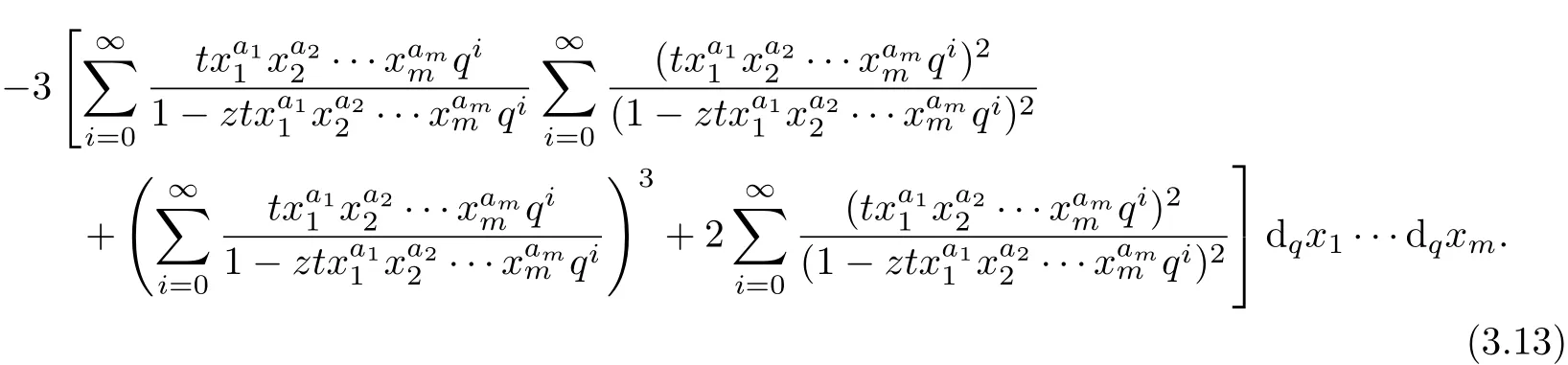
ProofDif f erentiating the equation(3.9)with respect to the the variable z

By

and

The result can be obtained.

Let m=2 in Theorem 7,we can get the following identity.

Corollary 5Let aibe real numbers with ai≥0,ji≥0(1≤i≤2)and|tx|＜1.

Then

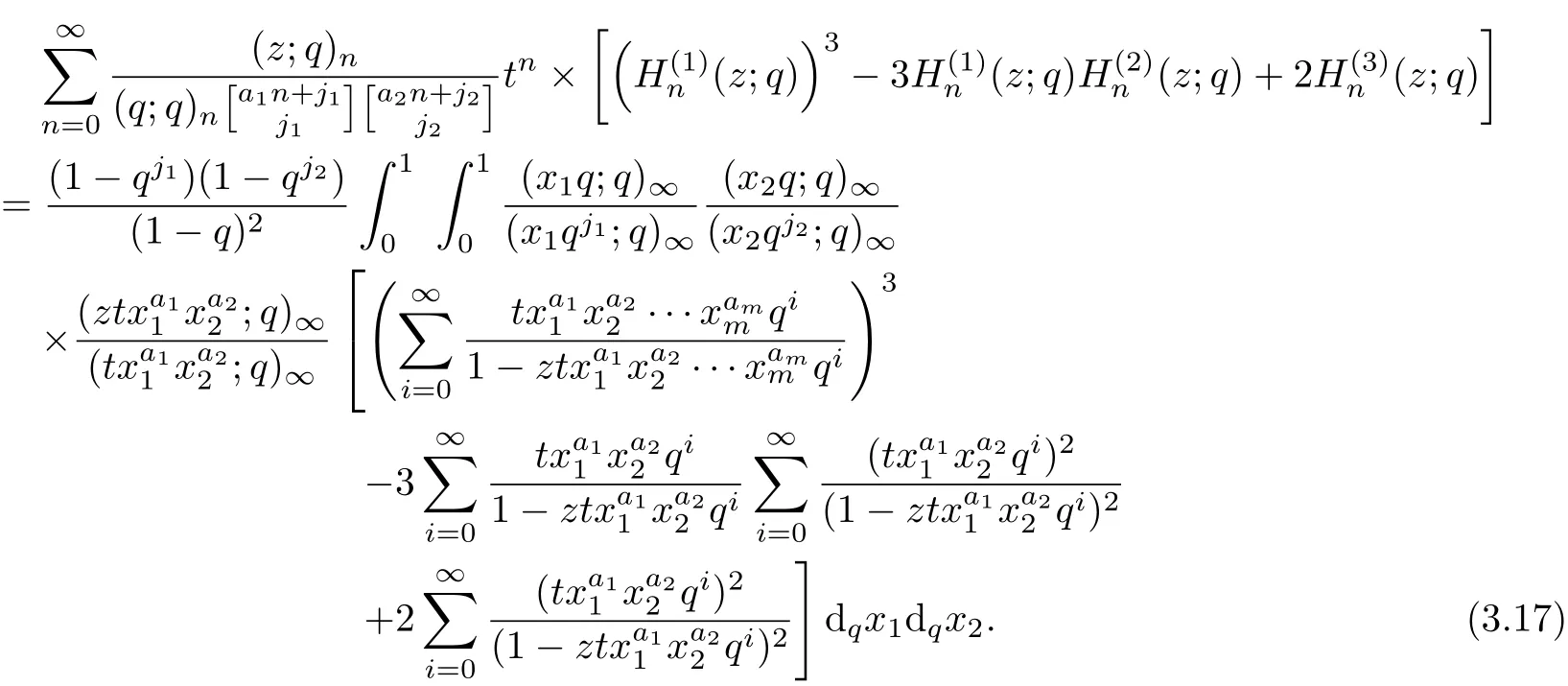
[1]GEORGE G,Mizan R.Basic Hypergeometric Series[M].Cambridge:Cambridge University Press,2004: 24-33.

[2]ANTHONY S.Sums of derivatives of binomial coefficients[J].Adv Appl Math,2009,42(1):123-134.

[3]ANTHONY S.Summation formula involving harmonic numbers[J].Analysis Math,2011,37(1):51-64.

[4]ANTHONY S.Integral forms of sums associated with harmonic numbers[J].Appl Math Comput,2009, 207(2):305-372.

tion:33D05,33C60,34A25

1002–0462(2014)04–0573–10

date:2013-03-03

Supported by the National Natural Science Foundation of China(10771093);Supported by the Youth Foundation of Luoyang Normal College(2013-QNJJ-001);Supported by the Youth Foundation of the Luoyang Institute of Science and Technology(2012QZ05)

Biographies:YANG Ji-zhen(1984-),female,native of Luoyang,Henan,a lecturer of Luoyang Normal College, M.S.D.,engages in combinatorial mathematics;WANG Yun-peng(1981-),male,native of Yingkou,Liaoning,a lecturer of Luoyang Institute of Science and Technology,M.S.D.,engages in combinatorial mathematics.

CLC number:O157.1Document code:A