计及车身弯曲变形和车轮侧偏的转向系统研究

严飞龙， 王国丽,2， 姜 宏

(1.北京理工大学 机械与车辆学院，北京 100081；2.吉林大学 汽车仿真与控制国家重点实验室长春 130025)

计及车身弯曲变形和车轮侧偏的转向系统研究

严飞龙1， 王国丽1,2， 姜 宏1

(1.北京理工大学 机械与车辆学院，北京 100081；2.吉林大学 汽车仿真与控制国家重点实验室长春 130025)

通过分析车身的纵向弯曲变形对赛车转向的影响，得出提高车身纵向弯曲刚度能减小因车身的弯曲变形而产生的侧偏角，提高转向时的操纵稳定性.运用有侧偏转向的阿克曼理论设计赛车的转向系统参数并运用Matlab中非线性最小二乘函数进行优化，使得内、外车轮的转角变化情况与考虑侧偏的理论阿克曼公式接近，轮胎的侧滑量为最小，从而提高了赛车在弯道中的操纵稳定性.

车身弯曲变形；车轮侧偏角；转向系统；操纵稳定性；阿克曼理论

大学生方程式(FSC)赛车使用的是钢管车身和超软轮胎.在转弯工况中，车身纵向弯曲刚度和轮胎刚度均小于乘用车，因此车身的弯曲变形和车轮侧偏角将对转向系统的影响很大.车辆在转向过程中最合理的状态是所有车轮绕同一个转动中心转动，但是实际上这种情况是不可能出现，只能通过合理设计和优化，使得其更接近理想状况，从而减少车轮在转向时的滑动量，提高赛车在弯道上的灵活性和操纵稳定性[1].

通过分析FSC赛车的车身纵向弯曲变形和车轮侧偏对转向特性的影响，提出了一种优化方案，优化结果满意.所应用的方法对车辆转向特性研究有一定的意义，为以后赛车的设计和应用提供了依据.

1 转向梯形的数学关系推导

FSC赛车采用断开式转向系统，假设车辆向左转弯，取图1所示坐标系，对内侧车轮的转向机构进行分析，可得齿条行程S与内轮转角的关系.

S=l1cos(γ-θi)+

.

(1)

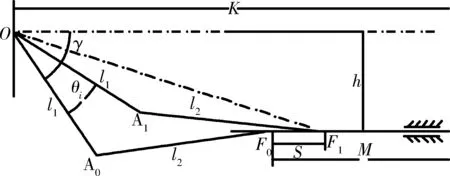
图1 内轮一侧杆系运动情况

外轮一侧则如图2所示，由于齿条左移行程S，通过右横拉杆拉动右梯形臂转动，可得行程S与外轮转角的关系.

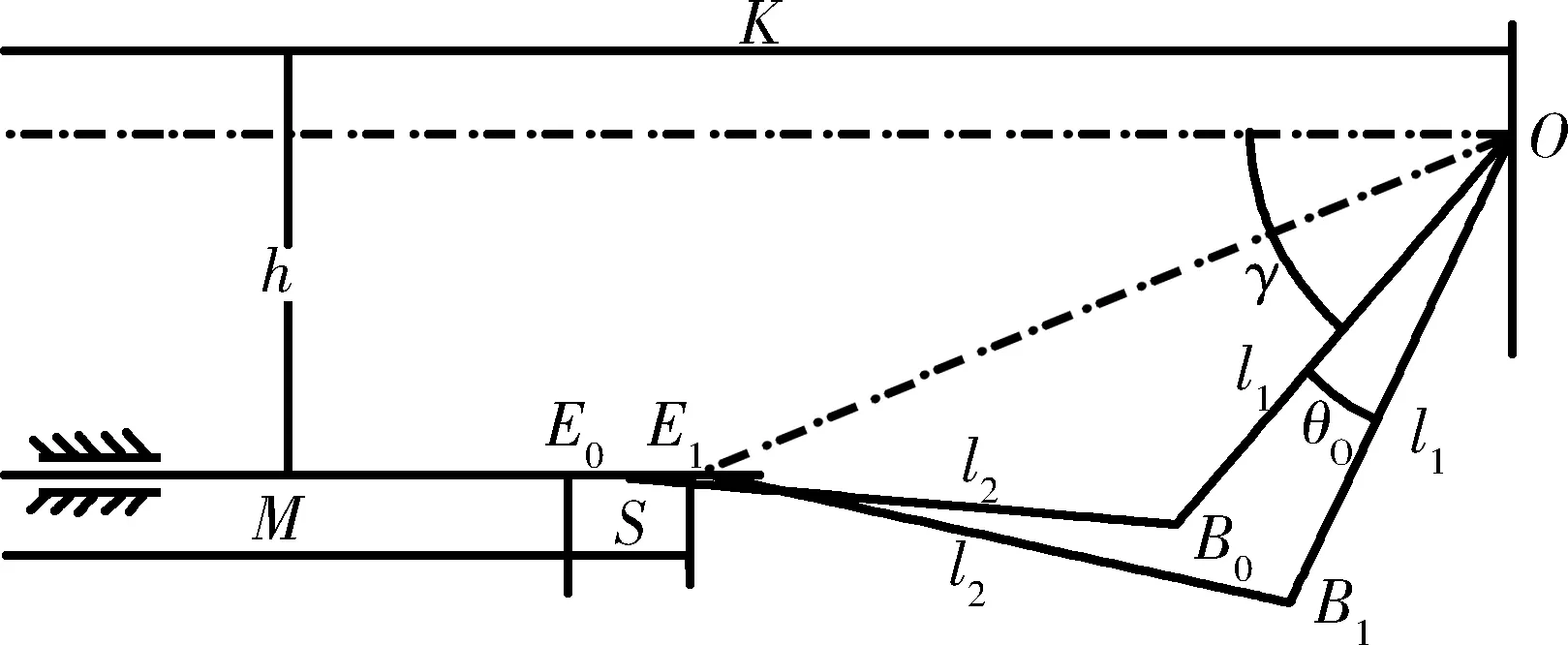
图2 外轮一侧杆系运动情况

由图可知：

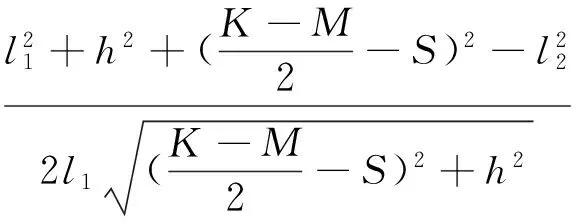
(2)

联立(1)、(2)式，消除S便可将θo表示为θi的函数,θo=φ′(θi).

2 车身的弯曲变形分析

FSC比赛赛道中弯道较多，且转弯半径较小，赛车在高速转弯时，侧向加速度可以达到1.5 g，此时车身不应视为刚体，车架纵向容易发生弯曲变形，导致前后车轮相对行进方向发生偏转[2].如图3所示，赛车向左转弯时前后车轮的偏转情况.

图3 车身弯曲变形时前、后车轮侧偏情况

整车质量为M；侧向加速度为Ay；质心处受到离心力F；前后悬架的内、外侧轮胎的横向摩擦力可以等效在前、后车桥的中心，分别为F1和F2；车架的纵向弯曲刚度为Kb，根据几何关系有

(3)

对整车横向进行受力分析

(4)

则前、后车轮因车身弯曲产生的侧偏角分别为

(5)

3 轮胎的侧偏特性分析

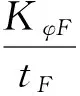
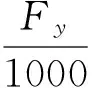
内外侧轮胎的侧向力与轮胎的垂直载荷成正比，整车前后轴荷分配比例为t:(1-t)，则前后桥的内外侧轮胎上的侧向力分别为

综上所述，得到前后桥的内外侧车轮侧偏角与整车的侧向加速度之间的关系如下所示：

假设该赛车的侧向弯曲刚度Kb=32 000 N/m，在转弯工况中侧向加速度的峰值为1.5 g，当侧向加速度在0与之间变化时，各轮胎的侧偏角的变化情况如图4所示.

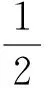
赛车在1.5g的最大侧向加速度工况中，各轮胎的侧偏角随着车身侧向弯曲刚度的变化情况如图5所示.加大车身侧向弯曲刚度能减小轮胎的侧偏角，有利于转弯工况中赛车的操纵稳定性.因此，如何设计车身，增大侧向弯曲刚度Kb是提高赛车在转弯工况中的操纵稳定性的关键所在.

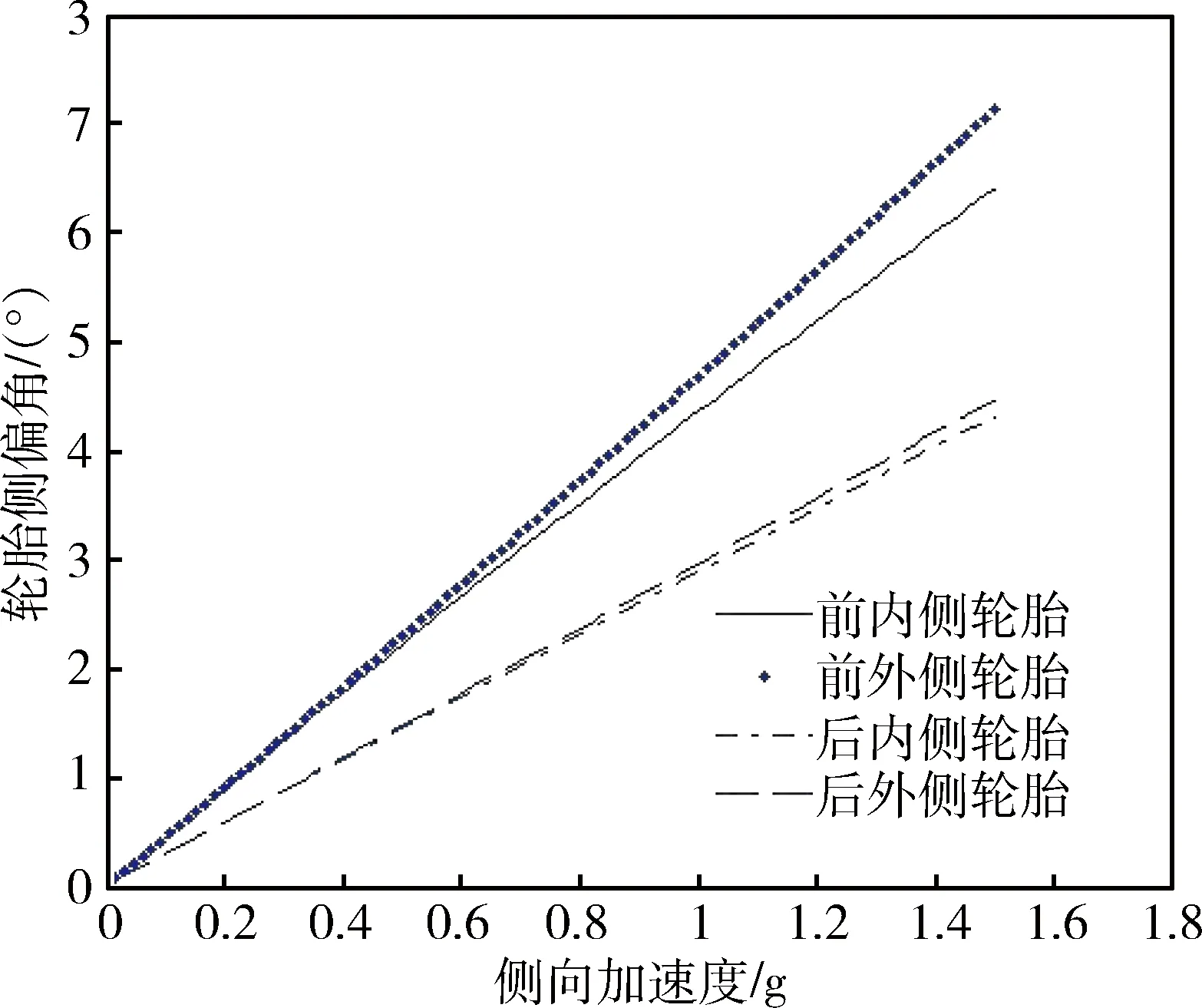
图4 各轮胎侧偏角变化曲线

图5 轮胎侧偏角随车身侧向弯曲刚度变化

4 有侧偏的阿克曼转角公式

车辆转向时，要获得良好的操纵稳定性，就要求内外转向轮行进方向一致，各轮胎不发生侧滑，即左右转向轮在转向过程中应尽量符合阿克曼公式[5].在有轮胎侧偏角存在的情况下，车辆转弯的情形如图6所示.

图6中，K为车辆主销轴线和地面交点连线的长度，L为轴距；L′为车辆主销轴线和地面交点连线与瞬时转动中心的距离.在理想状态下，要使全部车轮绕转向中心旋转，则必须满足下式

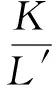
(6)

式中：

.

从而得到外侧车轮转角θO随着内侧车轮转角θi变化的理论关系式θO=φ(θi).优化转向梯形的结构参数，得到θi与θO之间实际的函数关系θO=φ′(θi)与理论关系式非常接近时，所有轮胎将不会发生侧滑，从而保证了车辆在弯道上的操纵稳定性.

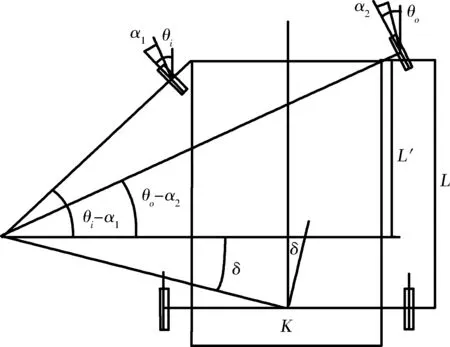
图6 存在侧偏角时车辆转弯示意图

5 优化设计

5.1 优化变量

FSC赛车的断开式转向系统左、右对称，取梯形一边进行优化.如图1所示，选取梯形底角γ、梯形臂长l1、齿条中心到梯形底边的安装距离h、横拉杆长度为优化变量l2，即X=[l1,l2,γ,h].

5.2建立目标函数

要实现所有车轮转向时近似做纯滚动，实际因变角θ0=φ'(θi)的变化情况应尽可能接近理论上的期望值θ0=φ(θi).引入加权因子，构成评价设计优劣的目标函数

f(x)=

(7)

其中加权因子为

5.3 约束条件

优化变量的预设值，以及变化范围如表1所示，即约束条件.

表1 优化变量的约束条件

在Matlab中，利用非线性最小二乘函数lsqnonlin(fun,x0,lb,ub,options)求解该最优问题，得到的变量优化结果为：X=[70.43,330.98,64.87°,35.92].外侧车轮转角随内侧车轮转角的初始、理论、实际优化变化情况如图7所示.

图7 内、外侧车轮转角变化情况

经过优化后实际的变化曲线更加接近理论的变化曲线，说明赛车在转弯工况中，四个车轮的转角接近理想阿克曼公式，赛车转向过程中的操纵稳定性得到了提高.优化前后的内、外侧车轮与理想变化情况的差值如图8所示.

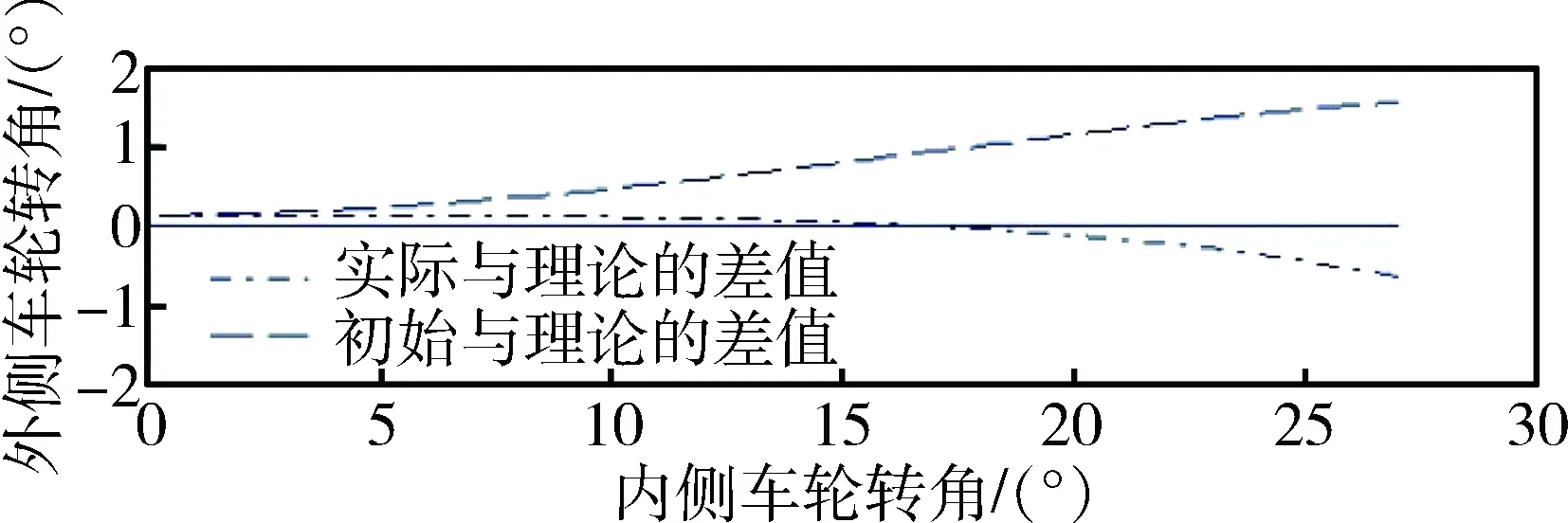
图8 优化前后与理论变化曲线的差值

可以看出，随着内侧车轮转角的增大，外侧车轮的转角与理论值的偏差总体上呈增大趋势，优化后的实际变化曲线与理论的差值要小于优化前，在内侧车轮最大转角处，优化后的差值从1.562 6°减小到0.641 3°，减小了59%.在大转角的工况下，操纵稳定性得到提高，优化结果满意.

6 结 论

FSC赛车在高速弯道工况中，车身在大的侧向加速度的影响下容易发生纵向弯曲变形，从而增大前后车轮的侧偏角.通过提高车身纵向弯曲刚度能减小因车身的弯曲变形而产生的侧偏角.同时，合理优化转向梯形，使得内外车轮的转角变化情况与考虑侧偏的理论阿克曼公式接近，轮胎的侧滑量为最小，从而提高了赛车在弯道中的操纵稳定性.

[1] 王霄锋，张小乐，胡 涛.轿车转向杆系的优化设计[J].清华大学学报(自然科学版),2004,44(11)：1528-1531.

[2] 周 兵，杨 凡，徐 琪.基于ADAMS的转向机构的优化设计[J].湖南大学学报：自然科学版，2008，35(12)：23-27.

[3] 曾 红，张志华，李铁军.基于ADAMS的横置液压缸式叉车转向系统的优化设计[J].机床与液压，2009,6(37)：179-182.

[4] 余志生，夏群生，赵六奇.汽车理论[M].北京：机械工业出版,2009.

[5] 伍文广，谷正气，李伟平.计及侧偏特性的转向系统分析和优化[J].湖南大学学报(自然科学版)，2011,38(5)：54-58.

Research on Steering System Considering Body deformation and Cornering Characteristics

YAN Fei-long1，WANG Guo-li1,2，JIANG Hong1

(1.School of Mechanical Engineering, Beijing Institute of Technology, Beijing 100081, China; 2.State Key Laboratory of Automotive Simulation and Control, Jilin University, Changchun 130025, China)

By analyzing the influence of the deformation of a racing car body on its cornering properties, it is summed up that increasing the longitudinal stiffness in bend of the body will help to reduce the sideslip angle of tire and to improve the cornering stability. By using Ackermann theory based on the cornering characteristics, the parameters of its steering system are designed and optimized by means of the nonlinear least square function in Matlab. The results show that the changes of the inner and outer sideslip angles of the wheels are close to the theoretical Ackermann formula based on the cornering characteristics, the lateral slip of the tires are minimized and the steering stability of the car is improved on the corner.

Longitudinal bending deformation of body; Sideslip angle of tire; Steering system; Handling and stability; Ackermann theory

1009-4687(2014)04-0035-05

2013-10-17

严飞龙(1988-)，男,研究生，研究方向车辆底盘.

U462

A