流化床内不同密度颗粒流动特性的数值模拟

李 斌， 周遵凯， 姚 路， 焦明月， 宋小龙

(1.华北电力大学 能源动力与机械工程学院，河北保定 071003;2.河北衡丰发电有限责任公司，河北衡水 053000)

流化床内不同密度颗粒流动特性的数值模拟

李 斌1， 周遵凯1， 姚 路1， 焦明月1， 宋小龙2

(1.华北电力大学 能源动力与机械工程学院，河北保定 071003;2.河北衡丰发电有限责任公司，河北衡水 053000)

将计算流体力学和离散单元法相结合，在自行开发程序上对流化床内随机生成的密度服从正态分布的颗粒的流动特性进行数值模拟，得到了不同床层表观气速下床内颗粒的流化过程图、气相速度场以及不同密度颗粒的速度场、体积分数沿床高的分布和分离率.结果表明：在较小床层表观气速下，床内不同密度的颗粒会出现分离现象，并且颗粒的密度差越大，颗粒分离越明显，当增大床层表观气速后，颗粒间的分离程度减弱；小密度颗粒的速度大于大密度颗粒，颗粒间的密度差越大，颗粒间的速度差也越大.

流化床； 离散单元法； 颗粒分离； 流动特性； 数值模拟

流化床燃烧技术作为一种新型的高效、低污染的清洁燃煤技术，在电力行业中得到了广泛的应用.在燃烧过程中，流化床内的煤颗粒随着成分发生变化其密度也会发生变化，同时由于流化床自身的特点，炉内脱硫需要向炉内添加脱硫剂以及在启动过程中加入循环物料，使得流化床内颗粒的密度具有极大的不均匀性.不同密度颗粒在床内的流动特性是不同的，当床层表观气速较小时，床内颗粒会出现分离.颗粒的混合和分离行为将影响颗粒在床内的分布、传热传质速率、床层膨胀及化学转换速率[1]，因此研究不同密度的颗粒在床内的流动特性更具有实际意义.

目前，已有学者对不同密度颗粒的流动进行了研究.刘阳等[2]采用硬球模拟方法对二维鼓泡流化床内非等密度双组分颗粒的流动特性以及弹性恢复系数对分层流动的影响进行了数值模拟.江茂强等[3]对2种不同表观气速下三维非等密度颗粒的气固两相流动进行了数值模拟，并对不同表观气速下床内颗粒的分层和混合进行了比较.袁竹林等[4-5]对不同密度和不同直径的颗粒进行了直接数值模拟，研究了不同密度和不同直径的颗粒在床内的运动规律.Ren等[6]对三维喷动床内等粒径非等密度的二元混合体系进行了数值模拟.Shoushtari[7]等对增压流化床内不同密度颗粒的混合和分离特性进行了研究.以上研究颗粒的密度均是直接给定的，具有一定的局限性.

数值模拟的关键是建立正确的数学模型，流化床内的气固两相流属于稠密气固两相流，对稠密气固两相流进行数值模拟的模型主要有2类：一是基于欧拉方法的双流体模型[8-9]；二是基于拉格朗日法的颗粒轨道模型[10-11].为了研究不同密度的颗粒在床内的运动情况，笔者采用随机数生成服从正态分布的颗粒密度，并将属于拉格朗日范畴的离散单元法和计算流体力学结合起来在自行编制的程序上对流化床内不同密度颗粒的流动特性进行了数值模拟，得到了不同床层表观气速下颗粒的流化过程图和气相速度场、不同密度颗粒的速度场和体积分数沿床高的分布以及不同密度颗粒的分离率随时间的变化趋势.

1 数学模型

将离散单元法和计算流体力学结合起来，建立模拟流化床内不同密度颗粒流动特性的数学模型.在拉格朗日坐标系下考察颗粒的运动，颗粒间的碰撞采用软球模型，根据牛顿第二定律建立每一个颗粒的运动方程，对每一个颗粒的运动进行求解.在欧拉坐标系下考察气相的运动，气相采用考虑气固耦合的Navier-Stocks方程，气相湍流模型采用k-ε两方程模型，并采用Simpler算法进行求解；气固两相间的耦合采用牛顿第三定律[12].

1.1 颗粒的运动方程和气相运动控制方程

颗粒在床内的运动主要受颗粒间的碰撞力、颗粒与壁面的碰撞力、气体对颗粒的曳力和颗粒自身重力作用.根据物理学定律，颗粒在床内的运动可分解为平动和转动.

平动运动方程为

(1)

式中：mi为颗粒i的质量；ui为颗粒速度；Fy,i为气体对颗粒的曳力；Fp为颗粒间的碰撞力，颗粒间的碰撞力采用软球模型计算[13].

转动运动方程为

(2)

Tij=Ri×ft,ij

(3)

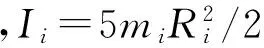
当颗粒i同时与周围的颗粒发生碰撞时，可通过矢量叠加计算颗粒i所受的合力和合力矩.

气相运动控制方程的求解过程见文献[13].

1.2 气体对颗粒的曳力

采用Gidaspow的曳力模型[14]，气体对颗粒的曳力为

当εg>0.8时，利用Wen & Yu等式可得

(4)

当εg≤0.8时，采用Ergun修正方程可得

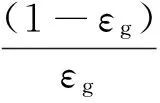
(ug-vp)Vp

(5)

(6)

式中：n为空隙率修正因子，一般n的取值为-4.65；Cd为单颗粒的曳力系数.

当Rep≤1 000时，

(7)

当Rep>1 000时，

Cd=0.44

(8)

Rep的计算式为

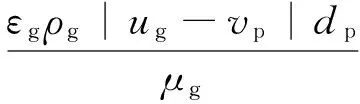
(9)

空隙率的表达式为

(10)

式中：ΔV为划分网格的体积；kc为所划分网格内颗粒的个数.

2 数值模拟对象

图1 颗粒密度的分布图

3 数值模拟结果

3.1 床内颗粒的流化过程图

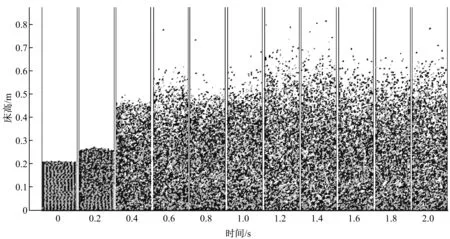
图2给出了床层表观气速v为1.6 m/s和2.27 m/s时0～2.0 s内床内不同密度颗粒的流化过程图，其中黑色代表中间密度颗粒，灰色代表大密度颗粒,其余代表小密度颗粒.从图2可以看出，初始时刻颗粒混合较均匀，在较小的床层表观气速下，随着流化气体的加入，床内颗粒逐渐流化，床层不断膨胀，起始阶段大密度颗粒在中小密度颗粒的推挤下跟随中小密度颗粒一起向上运动，但是随着时间的推移，大密度颗粒逐渐聚集在床层的中下部，尤其是靠近床层底部区域的大密度颗粒较多，小密度颗粒逐渐运动到床层中上部，床层底部区域小密度颗粒的数目逐渐减少，整体表现为大密度颗粒在床层的底部，小密度颗粒在床层上部，床内颗粒出现分离的现象.从图2还可以看出，增大床层表观气速后，颗粒的整体运动范围扩大，尤其是大密度颗粒，颗粒的分离程度减弱，但小密度颗粒的运动范围始终大于大密度颗粒.

3.2 气体速度分布

图3和图4分别给出了床层表观气速为1.6 m/s时，床内气体水平方向速度和垂直方向速度沿床高的分布，其中h为床高.由图3可知，在水平方向上，床层底部由于主气流的卷吸作用，喷口中心左侧的气体速度为正值，气体向右运动；右侧气体速度为负值，气体向左运动，两侧的气体向喷口中心聚集，在床层上部区域，气体分别向两侧扩散，并且随着床高的增加，气体水平方向速度减小.由图4可知，在垂直方向上喷口中心处气体的速度最大且为正值，靠近壁面两侧气体速度为负值，并且随着床高的增加呈减小的趋势.

3.3 颗粒速度分布

图5和图6分别给出了床层表观气速为1.6 m/s时不同密度的颗粒在水平方向和垂直方向的速度沿床高的分布.由图5可以看出，靠近床层底部的颗粒由于受到主气流的卷吸作用，喷口左侧的颗粒速度为正值，颗粒向右运动；右侧的颗粒速度为负值，颗粒向左运动，颗粒向喷口中心运动直到进入喷射区，床层上部的颗粒分别向壁面两侧运动.从图6可以看出，在垂直方向上，喷口中心位置处颗粒的速度为正值，颗粒向上运动；而靠近壁面两侧的颗粒速度为负值，颗粒向下运动，这是由于靠近壁面处气体的速度较小，气体对颗粒的曳力小于颗粒自身重力，颗粒向下运动，到达床层底部区域向喷口中心聚集进入喷射区，周而复始地形成了床内颗粒的内循环.此外，对比不同密度颗粒的速度可知，大密度颗粒的速度小于小密度颗粒，这是由于根据颗粒所受气体的曳力公式，相同粒径的颗粒在同一位置处所受曳力相同，但是其质量与密度成正比，因而不同密度的颗粒所获得的加速度不同，最后的速度也不同，密度大的颗粒的速度小于密度小的颗粒，并且密度差越大，速度差也就越大，不同密度间的颗粒相对滑移速度越大.由图5和图6还可以看出，颗粒的速度分布与气体的速度分布趋势基本一致，这是由于颗粒在运动过程中主要受气体对颗粒的曳力、颗粒自身重力及颗粒间的碰撞力所致.

(a)v=1.6 m/s

(b)v=2.27 m/s

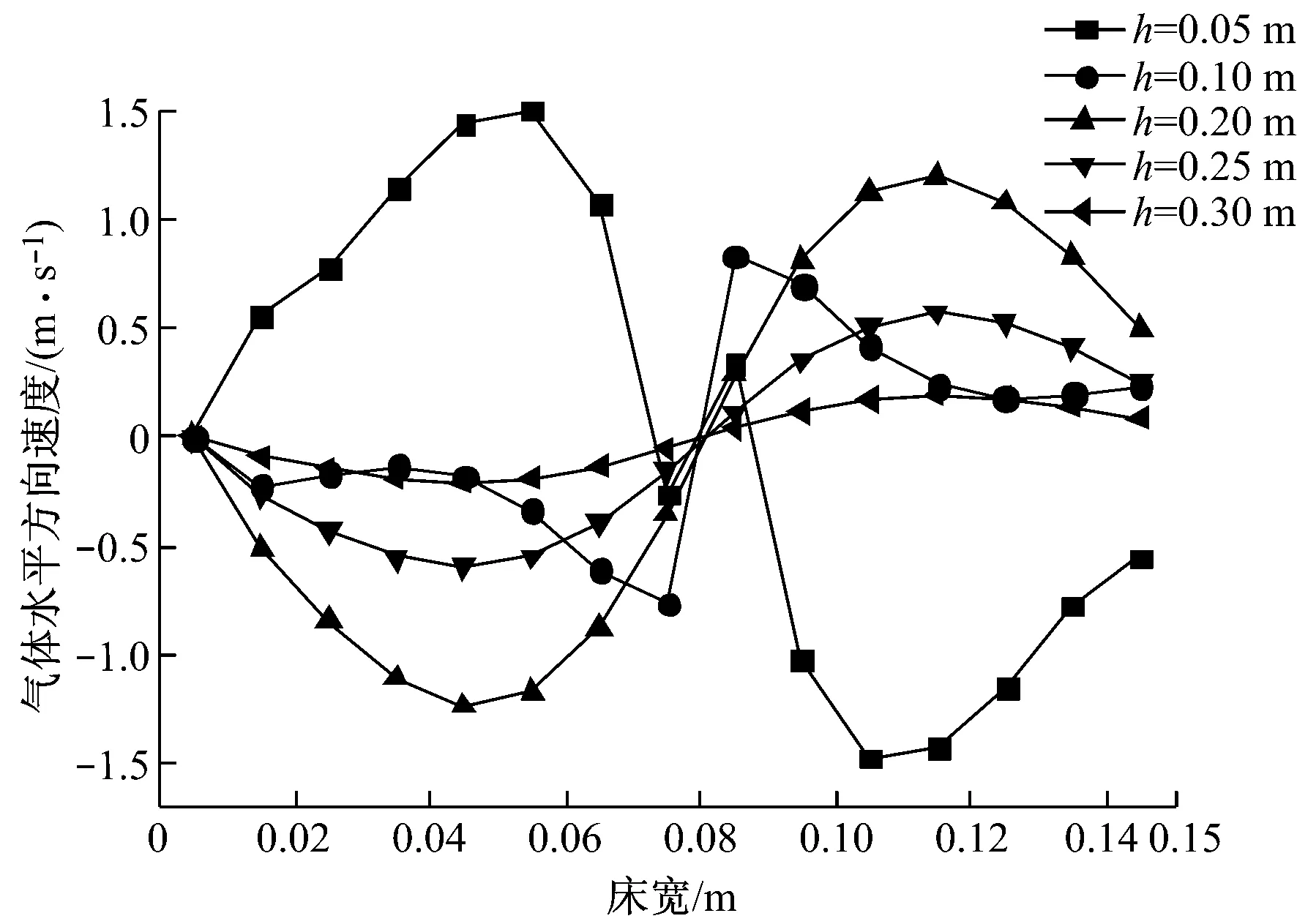
图3 气体水平方向速度

图4 气体垂直方向速度

图5 不同密度颗粒水平方向的速度分布

图6 不同密度颗粒垂直方向的速度分布

3.4 床内不同密度颗粒的体积分数沿床高的分布

图7和图8分别给出了床层表观气速为1.6 m/s和2.27 m/s时不同密度颗粒的体积分数沿床高的分布.从图7和图8可以看出，在初始时刻不同密度的颗粒体积分数沿床高的分布趋势基本一致，较小的床层表观气速下，在1.0 s左右床高0.3 m以下大密度颗粒的体积分数逐渐大于中小密度颗粒，床高0.3 m以上小密度颗粒的体积分数逐渐大于中大密度颗粒，颗粒逐渐出现分离现象，并且随着时间的推移，颗粒的分离现象逐渐明显.但是在较大的床层表观气速下，不同密度的颗粒并没有出现较小床层表观气速下明显的颗粒分离现象，只是在1.5 s后床高0.6 m以上小密度颗粒的体积分数大于中大密度颗粒.由此可见，增大床层表观气速后，不同密度颗粒的分离程度减弱，并且不同密度颗粒发生分离的起始时间延迟，发生分离的位置沿床高提高.这是由于增大床层表观气速后，床内不同位置的气体速度均有所增大，颗粒所受的曳力增大，颗粒的运动范围扩大，有利于减弱颗粒的分离.

(a)t=0.02s(b)t=0.5s(c)t=1.0s(d)t=1.5s(e)t=2.0s

图7v=1.6 m/s时不同密度颗粒的体积分数沿床高的分布

Fig.7 Distribution of volume fraction of different density particles along bed height at 1.6 m/s

(a)t=0.02s(b)t=0.5s(c)t=1.0s(d)t=1.5s(e)t=2.0s

图8v=2.27 m/s时不同密度颗粒的体积分数沿床高的分布

Fig.8 Distribution of volume fraction of different density particles along bed height at 2.27 m/s

3.5 不同密度颗粒的分离率

采用颗粒分离率[15]对不同密度的颗粒在流化过程中的分离程度进行定量分析，颗粒分离率s的定义为

(11)

(12)

(13)

(14)

式中：hi为某一组分颗粒的平均床高；wi为颗粒的质量分数；φs,k为计算网格内颗粒的体积分数；Vk为计算网格的体积；hk为计算网格中心的高度；Ncells为所有网格的数目.

图9给出了床层表观气速为1.6 m/s和2.27 m/s时，床内不同密度颗粒的分离率随时间的变化趋势.由图9可知，在较小的床层表观气速下，不同密度颗粒的分离率随着时间的推移不断增大，并且颗粒的密度差越大，颗粒的分离率也越大.对比不同床层表观气速下颗粒的分离率可知，增大床层表观气速后，颗粒出现明显分离的时刻向后延迟，同时颗粒的分离率减小，不同密度颗粒的分离程度减弱.

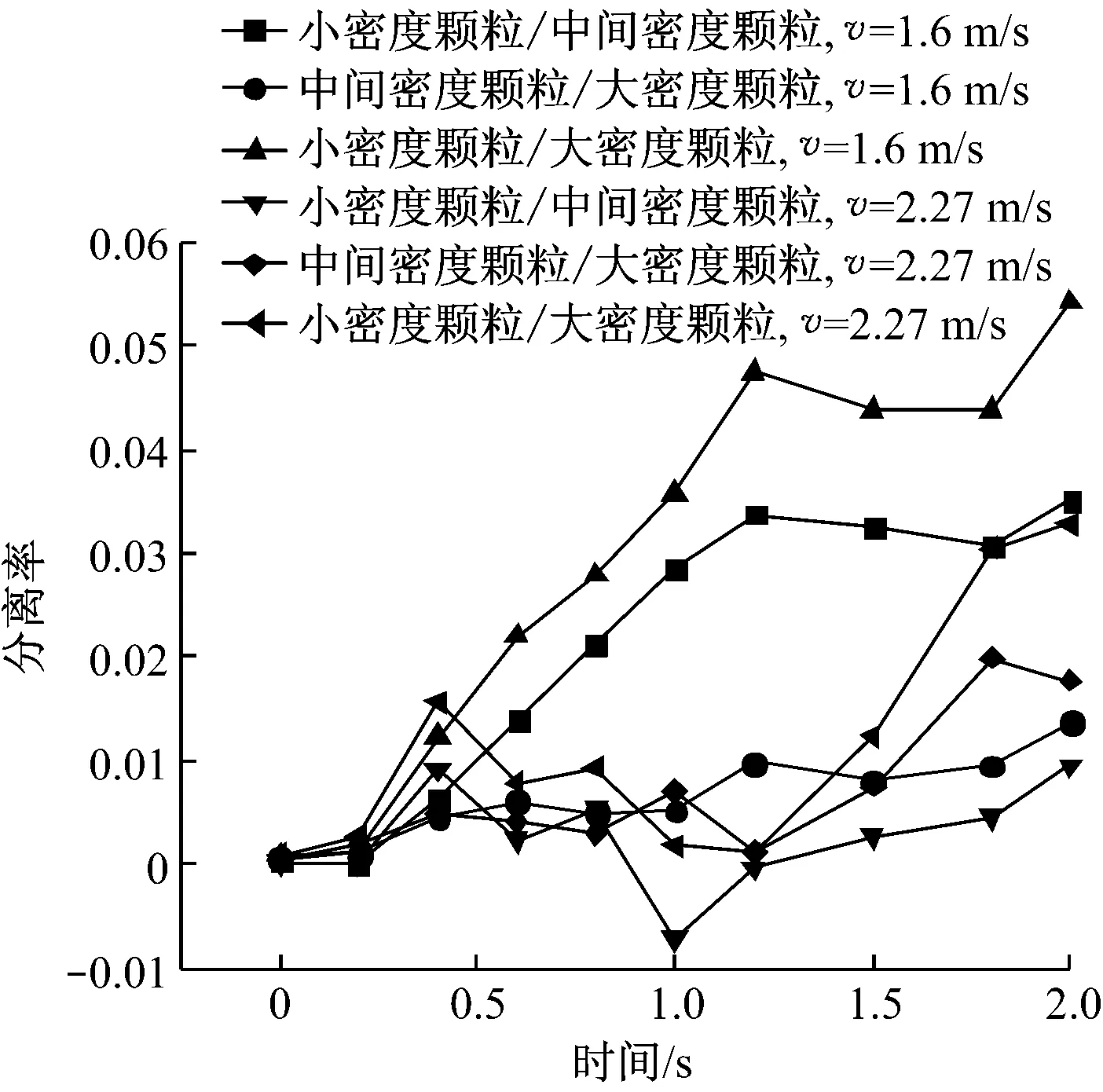
图9 不同床层表观气速下不同密度颗粒的分离率随时间的变化

Fig.9 Variation of segregation rate of different density particles with time at different superficial gas velocities

4 结 论

(1)在水平方向上，床层底部喷口中心左侧气体速度为正值，右侧气体速度为负值，气体向喷口中心聚集，在床层上部区域气体分别向两侧扩散，并且随着床高的增加，气体速度减小.在垂直方向上，中间气体速度较大且为正值，靠近壁面两侧的气体速度为负值，并且随着床高的增加，气体速度减小.

(2)颗粒速度沿床高的分布与气体速度的分布趋势基本一致，并且小密度颗粒的速度大于大密度颗粒，密度差越大，颗粒间的速度差也越大.

(3)在床层表观气速较小时，不同密度的颗粒出现分离现象，整体表现为大密度的颗粒聚集在床层底部区域，小密度颗粒在床层上部区域，小密度颗粒的运动范围大于大密度颗粒.当增大床层表观气速后，不同密度颗粒发生较明显分离的位置提高，发生分离的时刻向后延迟，颗粒分离的程度减弱.

[1] OLAOFE O O，BUIST K A，DEEN N G，etal．Segregation dynamics in dense polydisperse gas-fluidized beds[J]．Powder Technology，2013,246:695-706．

[2] 刘阳，刘文铁，何玉荣，等．流化床内非等密度双组分颗粒流动特性的研究[J]．热能动力工程，2005，20(6):62-65．

LIU Yang，LIU Wentie，HE Yurong，etal．A study of the flow characteristics of non-isodensity and dual-component particulates in a fluidized bed[J]．Journal of Engineering for Thermal Energy and Power，2005，20(6):62-65．

[3] 江茂强，赵永志，郑津洋．非等密度颗粒气固流化床的微观尺度模拟与分析[J]．浙江大学学报：工学版，2009，43(9):1703-1708．

JIANG Maoqiang，ZHAO Yongzhi，ZHENG Jinyang．Micro-scale simulation and analysis of gas-solid fluidized bed with multi-density distribution of particles[J]．Journal of Zhejiang University：Engineering Science，2009，43(9):1703-1708．

[4] 袁竹林，马明．稀疏气固两相流动中颗粒分离特性的数值模拟[J]．燃烧科学与技术，2001，7(4):235-238．

YUAN Zhulin，MA Ming．Numerical simulation of particle segregation in dilute gas solid two-phase flow[J]．Journal of Combustion Science and Technology，2001，7(4):235-238．

[5] 袁竹林．流化床中颗粒流化运动的直接数值模拟[J]．燃烧科学与技术，2001，7(2):120-122．

YUAN Zhulin．Study on fluidized region of particles using direct simulation method[J]．Journal of Combustion Science and Technology，2001，7(2):120-122．

[6] REN B，SHAO Y，ZHONG W，etal．Investigation of mixing behaviors in a spouted bed with different density particles using discrete element method[J]．Powder Technology，2012，222:85-94．

[7] SHOUSHTARI N A，HOSSEINI S A，SOLEIMANI R．Investigation of segregation of large particles in a pressurized fluidized bed with a high velocity gas: adiscrete particle simulation[J]．Powder Technology，2013，246:398-412．

[8] 何玉荣，陆慧林，别如山，等．鼓泡流化床宽筛分颗粒气固两相流动的流体动力学[J]．动力工程，2003，23(5):2646-2651．

HE Yurong，LU Huilin，BIE Rushan，etal．Hydrodynamics of gas-solid flow in bubbling fluidized bed with wide particle size distribution[J]．Power Engineering，2003，23(5):2646-2651．

[9] CHANG J，WANG G，GAO J，etal．CFD modeling of particle-particle heat transfer in dense gas-solid fluidized beds of binary mixture[J]．Powder Technology，2012，217:50-60．

[10] XU B H，YU A B．Numerical simulation of the gas-solid flow in a fluidized bed by combining discrete particle method with computational fluid dynamics[J]．Chemical Engineering Science，1997，52(16):2785-2809．

[11] 李斌，宋小龙．循环流化床内颗粒混合特性的数值模拟[J]．动力工程学报，2013，33(10):759-764．

LI Bin，SONG Xiaolong．Numerical simulation on mixing characteristics of particles in circulating fluidized bed [J]．Journal of Chinese Society of Power Engineering，2013,33(10):759-764．

[12] 纪律．循环流化床流动及磨损特性的DEM数值模拟[D]．保定:华北电力大学，2011．

[13] 李斌，纪律．流化床炉内颗粒混合的离散单元法数值模拟[J]．中国电机工程学报，2012，32(20):42-48．

LI Bin，JI Lü．Numerical simulation of particle mixing in circulating fluidized bed with discrete element method[J]．Proceedings of the CSEE，2012，32(20):42-48．

[14] DEEN N G，VAN S A M，VAN D H M A，etal．Review of discrete particle modeling of fluidized beds[J]．Chemical Engineering Science，2007，62(1):28-44．

[15] GOLDSCHMIDT M，LINK J M，MELLEMA S，etal．Digital image analysis measurements of bed expansion and segregation dynamics in dense gas-fluidised beds[J]．Powder Technology，2003，138(2):135-159．

Numerical Simulation on Flow Characteristics of Different Density Particles in a Fluidized Bed

LIBin1,ZHOUZunkai1,YAOLu1,JIAOMingyue1,SONGXiaolong2

(1. School of Energy, Power and Mechanical Engineering, North China Electric Power University,Baoding 071003, Hebei Province, China; 2. Hebei Hengfeng Power Generation Co., Ltd., Hengshui 053000, Hebei Province, China)

Numerical simulation was conducted on the flow characteristics of different density particles in a fluidized bed, whose density is randomly generated and obeys normal distribution, with self-developed program combining computational fluid dynamics and the discrete element method, during which the fluidization process of different density particles at different superficial gas velocities, the gas velocity field, the particle velocity, the distribution of volume fraction along bed height and the segregation rates were obtained. Results show that separation phenomenon appears in different density particles at relatively low superficial gas velocities; the larger the density difference is, the more obvious the separation phenomenon will be, which weakens with the rise of superficial gas velocity. The velocity of small density particles is greater than that of large ones, and the larger the density difference is, the greater the velocity difference will be.

fluidized bed; discrete element method; particle separation; flow characteristic; numerical simulation

1674-7607(2014)12-0932-06

TK224

A

470.10

2014-03-10

2014-04-24

李 斌(1969-)，男，河北保定人，副教授，博士，主要从事气固两相流数值模拟方面的研究.电话(Tel．)：0312-7522917； E-mail：binli.ncepu@gmail.com.