基于“复杂人”假设的增长社会网络模型

王金平等高玉静 王德华

（山东科技职业学院基础部,山东潍坊 261053）

基于“复杂人”假设的增长社会网络模型

王金平等高玉静 王德华

（山东科技职业学院基础部,山东潍坊 261053）

以组织行为学中“复杂人”假设作为个体的基本假设，提出基于“效用最大化”和“朋友的朋友”的建边规则，构造一个基于个体选择的增长社会网络模型，利用计算机仿真的方法研究该模型的小世界特性、集聚性、同配性等结构特性，证明该网络的度分布、集聚性、层次性、小世界特性、同配性同现实网络更为拟合。该模型有助于了解复杂社会网络形成的机理，并进一步认识社会网络中的一些参数可能对网络拓扑结构造成的影响。

社会网络；结构特性；效用最大化；朋友的朋友；复杂网络

1 引言

自从Barabási和Albert在对互联网的研究中发现网络的无标度特性后，各行各业的研究者在不同的研究领域中都发现了网路的无标度特性。这对传统的描述复杂网络的随机图模型提出了前所未有的挑战。基于对随机图模型和现实网络特性的深入分析，Barabási和Albert提出了“成长”和“择优连接”两种连接机制，从而从理论上解释了现实中大规模网络的无标度特性。此后，涌现出大量的研究关注于如何通过各种不同的机制生成复杂网络的无标度特性。

社会网络的拓扑结构对于社会网络的产出起着至关重要的作用。这样的例子包括学术合作者关系网络、公司间的合作研究网络、政治联盟、贸易网络以及通过人际交往网络共享工作职位信息等。鉴于社会网络的拓扑结构如此重要，研究社会网络形成的原因和机制是非常有价值的。

然而，到目前为止，对于复杂网络的研究多数集中于自然网络、技术网络等领域，对于社会网络的研究非常有限[1-2]。近年来的研究发现，同自然、技术网络相比，社会网络具有许多独特的拓扑属性[3-7]。例如，小世界特征就是社会网络的一种最具代表的拓扑特性，具有小世界特征的社会网络通常称为小世界网络，具有较短的平均路径长度，又具有较高的聚集系数；现实世界中小世界网络也很常见，大部分人的朋友都是和他们住在同一条街上的邻居（平均路径短的特征），或在同一单位工作的同事（聚集性高的特征）。这就需要从社会网络的成员特质出发，识别并捕捉对网络拓扑结构形成起作用的影响因素的动态变化过程，探索社会网络拓扑结构的形成机理。然而，对社会网络的建模却一直没有得到应有的重视。现有的社会网络建模多数从数学机理出发，忽视了社会网络成员的个体选择。同时，研究者所建立的社会网络模型都只能生成社会网络的部分结构特性，还没有能够全面反映社会网络各种结构特性的网络模型[8-12]。

本文以组织行为学中 “复杂人”假设作为社会网络成员的基本假设，提出了社会网络的两种建边机制，构建了一个增长社会网络模型。数值模拟表明，该模型能够较全面地满足大规模社会网络的主要结构特性。

2 模型节点的个体选择

考察社会网络的构成，其节点代表人或其他的社会实体，边代表实体间交互作用、合作或相互影响等关系。相对于自然网络的节点，作为社会网络的成员，人具有智能、感情和自我决策的能力。因而，其形成原因也更为复杂。然而，节点间边的变化归根结底是由个体选择决策的。

然而个体选择决策是以潜在的个体人性假设为基础的，比如 “效用最大化”原则实质上归结于“经济人”假设，体现了个体的理性；“朋友的朋友”原则实质上归结于“社会人”假设，体现了个体的感性。但是随着组织行为学的发展和研究的深入，学者们提出了更全面的个体假设——“复杂人”假设，认为个体同时具有理性和感性的一面，所以个体的选择决策原则中也应该体现这两方面的特征。

“效用最大化”原则来源于经济学中的理性经济人假设。经济学中通常假定经济人在决策时遵循个人效用最大化的原则，按照利己的原则进行决策。经济人在建立连接时，总是试图最大化自己的效用，从他人那里获得尽可能多的资源。BA无标度模型中的择优连接在一定程度上体现了这种原则。然而，在BA模型中，节点的优势仅仅体现在节点的连接数量上。而在实际生活中，连接数量仅仅是个体的资源之一。每个个体，不管是人，还是企业、团体，都还存在着地位、财富等其他独特的资源或特点。在很大程度上，社会网络中成员的优势正是来源于这些其他的资源。比如说，人际交往中那些本身地位较高或者财富较多的人更容易受到人们的关注，更多的人愿意成为他们的朋友。而在引文网络中，某些高质量论文可能暂时引用量并不大，在网络中连接数量较小，然而由于其本身的高质量，其可能在随后受到关注，而在短时间内获得大量的引用。而BA模型无法体现出这些其他的资源和特点。在BA模型中节点除了连接数量的差异，是完全同质的。

“朋友的朋友”原则，即朋友的朋友更容易成为朋友。这种原则在一定程度上体现了人的感性因素。在生活中，朋友的朋友更容易给我们亲切感，让我们更加信任，从而更容易成为朋友。而在经济网络中，出于对合作伙伴的信任，企业更容易与合作伙伴的合作伙伴建立合作关系。另外，在人际关系网络中，由于朋友关系，成员与朋友的朋友交往的机会相对较多，更容易成为朋友，产生了朋友圈的重叠。这种现象在现实中也较为常见。而在经济网络中，由于可以从合作伙伴那里获得更多其合作伙伴的信息，因而这种传递性也很容易得到实施。

以下，将基于这两条原则，来确定模型中节点的个体选择。首先借鉴Jackson和Watts提出的连接模型定义模型中的效用函数。JW模型主要是描述经济学中的合作问题[8]。根据他们的连接模型，行为主体通过所有的直接和间接连接获得收益。间接联结可获得的收益小于直接连接获得的收益，行为主体从其他主体那里获得的效用取决于二者之间的路径长度。

因此，成员i从网络中获得的效用为，

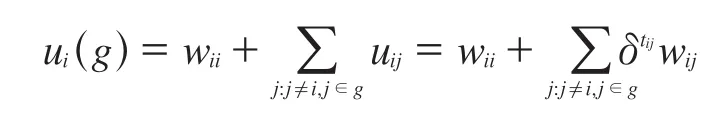
其中，δ为边际收益；tij表示成员i，j间的最短距离；δtij表示收益随成员i，j间的最短距离而递减；wij表示节点j对节点i的固有价值。

其次，对于wij的定义，借鉴了Adamic等提出的增长模型中的定义[13]，成员均匀地分布在二维空间中，每维空间代表一种成员特征，比如成长背景、行业领域等，成员坐标（xi, yt）代表其不同的特征值，两个成员之间的特性差异为：

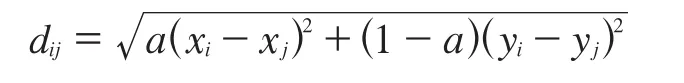
其中，a控制着不同特征对于成员交往的相对重要性。

于是i对于j的固有效用为：

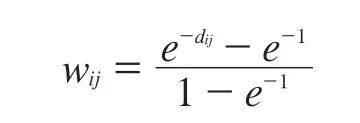
j对i的固有效用为wji=wij。

于是效用函数可改为：

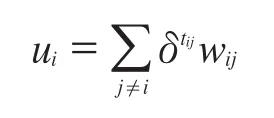
在定义了节点的效用函数后，接下来开始建立增长社会网络模型。

（1）初始状态：初始网络为m个初始节点随机均匀分布在二维空间中，节点之间链状连接；

（2）增长：每个时刻，一个新节点i加入到网络当中，该节点带有l条边；

（3）连接：新节点i加入网络后，首先按照“效用最大化”规则选择一个网络中已有的节点建边，与节点i连接的概率为其中与新节点同节点i连接所可能获得的效用成正比，具体形式如下：

然后，以概率p采用“朋友的朋友”原则建立剩下l-1条边：在初始节点的所有邻居中按照“效用最大化”规则建立l-1条连接；以概率l-p在除了初始节点之外的所有节点中采用“效用最大化”原则建立剩下l-1条连接。

3 网络结构的特性

3.1 度分布特征

（1）p的变化对度分布的影响

这里主要考虑两种极端的情况，当δ=0和δ=1时，p的变化对度分布的影响。首先考虑当δ=0时，p的变化对度分布的影响。

如图1（a），当δ=0，p=0时，网络度分布呈现指数分布。这是因为每一时刻新节点按照“效用最大化”原则建立l条连接，这里节点之间相对效用仅由两个节点的相对位置决定，而新节点位置是随机均匀分布的，所以每一时刻，每个老节点被选择的概率完全一样，新节点的所有连接都没有偏好。

如图1（b），当δ=0，p=1时，网络度分布呈现幂律分布。这是因为每一时刻新节点首先按照“效用最大化”原则建立一条初始连接，然后在此节点的邻居中再按照“效用最大化”原则建立l-1条二次连接，这里节点之间相对效用仅由两个节点的相对位置决定，而新节点位置是随机均匀分布的，所以每一时刻，在新节点建立初始连接时，每个老节点被选择的概率完全一样。但是在新节点建立二次连接时，度大的节点被选择的概率大，度大的节点是很多节点的邻居，以邻居身份被选的可能性就大一些，所以此时新节点是有连接偏好的，偏向于连接度大的节点。由此可见，新节点的初始连接是没有偏好的，但是二次连接是有偏好的，偏向于连接度大的节点。

下面考虑当δ=1时，p的变化对度分布的影响。

如图2（a），当δ=1，p=0时，网络的度分布呈现幂律分布。这是因为每一时刻新节点按照“效用最大化”原则建立l条连接，这里老节点i对新节点j的效用不仅包括i对j固有效用，还包括i的所有邻居节点对j的固有效用之和，这样邻居多的节点被连接的概率就大一些。也就是说，新节点的所有连接都是有偏好的，偏向于连接度大的节点，所以网络度分布呈现幂律分布。

如图2（b），当δ=1，p=1时，网络的度分布呈现幂律分布。这是因为每一时刻新节点首先按照“效用最大化”原则建立一条初始连接，然后在此节点的邻居中再按照“效用最大化”原则建立l-1条二次连接，这里老节点i对新节点j的效用不仅包括i对j固有效用，还包括i的所有邻居节点对j的固有效用之和，这样邻居多的节点被连接的概率就大一些。也就是说，新节点的所有连接都是有偏好的，偏向于连接度大的节点，所以网络度分布呈现幂律分布。

由此可以看出，保持δ=0不变，控制参数p由0增大到1，可以得到网络度分布存在指数分布、介于指数分布和幂律分布之间的分布、幂律分布这3种形式；保持δ=1不变，控制参数p由0增大到1，虽然得到的网络度分布均为幂律分布，但是可以得到指数值不同的幂律分布。

（2）δ的变化对度分布的影响

这里同样首先考虑两种极端情况，当p=0和p=1时，δ的变化对度分布的影响。

p=0、δ=0；p=0、δ=1；p=1、δ=0；p=1、δ=1对应的度分布图都可以在图2、图3中找到，各自的分析也可以在p的变化对度分布的影响分析中找到，在此不再赘述。

图1 (a)δ=0，p=0时网络节点度分布图

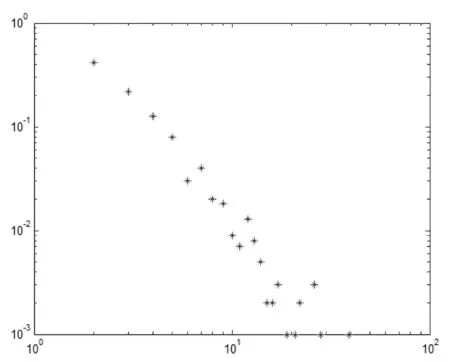
图1 (b)δ=0，p=1时网络节点度分布图

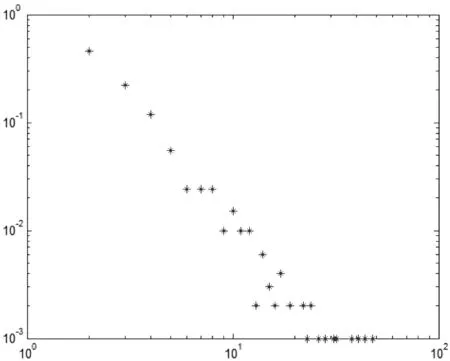
图2 (a)δ=1，p=0时网络节点度分布图

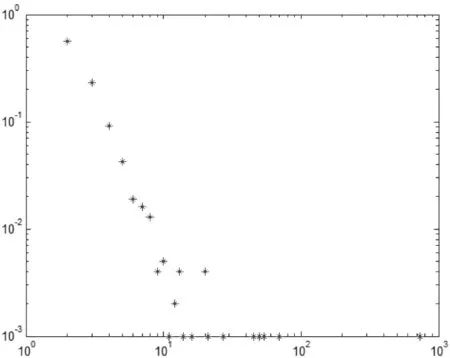
图2 (b)δ=1，p=1时网络节点度分布图

由此可以看出，保持p=0不变，控制参数δ由0增大到1，可以得到网络度分布存在指数分布、介于指数分布和幂律分布之间的分布、幂律分布这3种形式；保持p=1不变，控制参数δ由0增大到1，虽然得到的网络度分布均为幂律分布，但是可以得到指数值不同的幂律分布。

总结以上两种分析，都与实证的社会网络度分布吻合。实证研究表明，许多社会网络的顶点度分布并不能呈现出完全的无标度。在电影演员网络和一些协作网络中常见的是带指数截点的幂律形式。而在熟人网络中网络的度分布由两段幂律分布组成，且度较小的部分其幂律指数较小，整体可以近似看作指数分布。社会网络的度分布范围通常不会像自然网络那么宽，不存在度非常大的节点。

效用的传递性越强，网络中节点的度分布就越不均匀；反之，网络中节点的度分布就越均匀。

3.2 小世界特征

网络中任意一对不相邻的节点之间的路径长度，指连通两节点的路径上所经过的节点个数，其中节点个数最少的路径长度称为最短路径长度。网络中任意一对节点之间的最短路径长度的平均值叫做网络的平均最短路径。如图5给出了当δ=0. 6，p=0. 6时平均最短路径随节点数量的变化情况，可以看出，随着节点数量的增加，模型的平均路径长度增长速度逐渐变小，l～lnN。从图5中可以看出，当节点增加到一定数量后平均最短路径的增长趋于缓和，取值在4～5之间，这与小世界现象的实验值几乎吻合。因此，通过实验证明：在δ和p所有的参数组合下，平均最短路径长度随着节点数的变化都符合小世界特征。

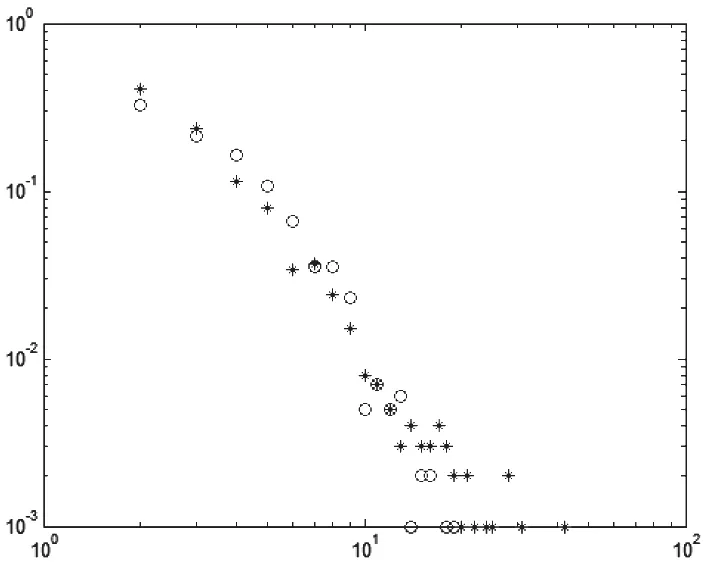
图3 (a)δ=0，p=0（ o ）；δ=0，p=1（*）时节点度分布图

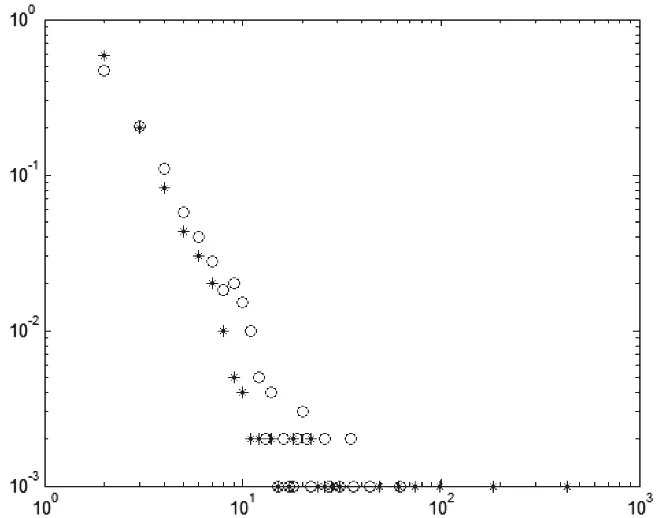
图3 (b)δ=1，p= 0（ o ）；δ=1，p= 1（*）时节点度分布图

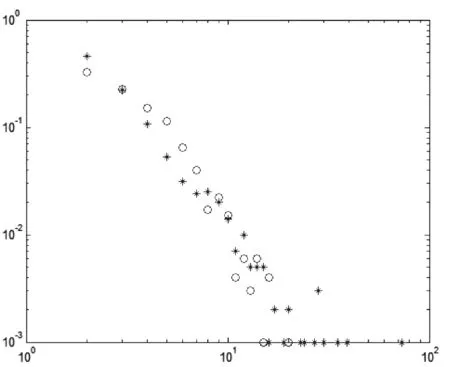
图4 (a)p=0，δ=0（ o ）；p=0，δ=1（*）时节点度分布图

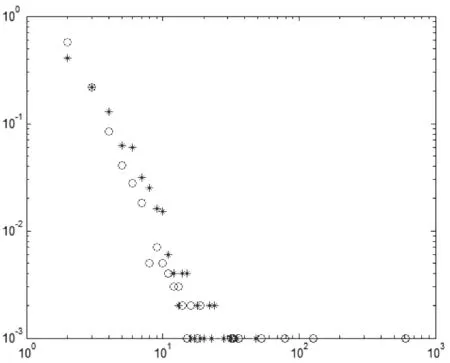
图4 (b)p=1，δ=0（ o ）；p=1，δ=1（*）时节点度分布图

3.3 聚集性特征

在本模型中，利用“朋友的朋友”这一择优原则来生成较大的集聚系数。这来源于生活中人们交友时的习惯。在每一轮中，网络个体以概率p选择朋友的朋友建立二次连接。这样很显然可以在网络中生成更多的三角形，从而提高网络的聚集系数。

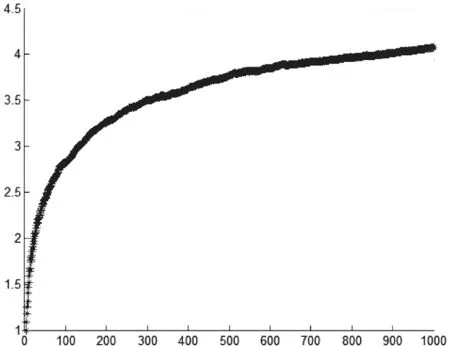
图5 δ=0.6，p=0.6时，平均最短路径随节点数量的变化图

图6给出了不同效用传递系数（δ）值下聚集系数随策略选择概率（p）的变化情况。可以看出：当δ不变时，随着参数p的增大，聚集系数越来越大，而且几乎为线性关系。

因为节点越来越多地采取“朋友的朋友”的择友策略，选择同“朋友的朋友”建立连接，从而在网络中形成了更多的“三角形”结构，导致网络的聚集系数不断增大。当p=0时，模型即等同于前述以“效用最大化”建边的模型，模型生成的网络聚集系数接近0；当p 达到1时，模型等同于以“朋友的朋友”原则建边，网络的聚集系数可以达到0.7～0.8。

3.4 同配性特征

图7给出了不同效用传递系数（δ）值下同配性系数随策略选择概率（p）的变化情况。可以看出：当δ不变时，随着参数p的增大，同配性系数越来越小，而且几乎为线性关系。

因为从对度分布的分析可知，随着p的增加，网络从指数分布过度到标准的幂律分布，网络中节点的度分布越来越不均匀，当以平均最短路分析中的δ=1时，p从0到1的过度中，以网络的度分布和网络图为例，网络中的hub节点越来越明显，最终当p=1时，几乎所有小节点都与同一个巨大的hub节点相连，网络的同配性降到了最低。

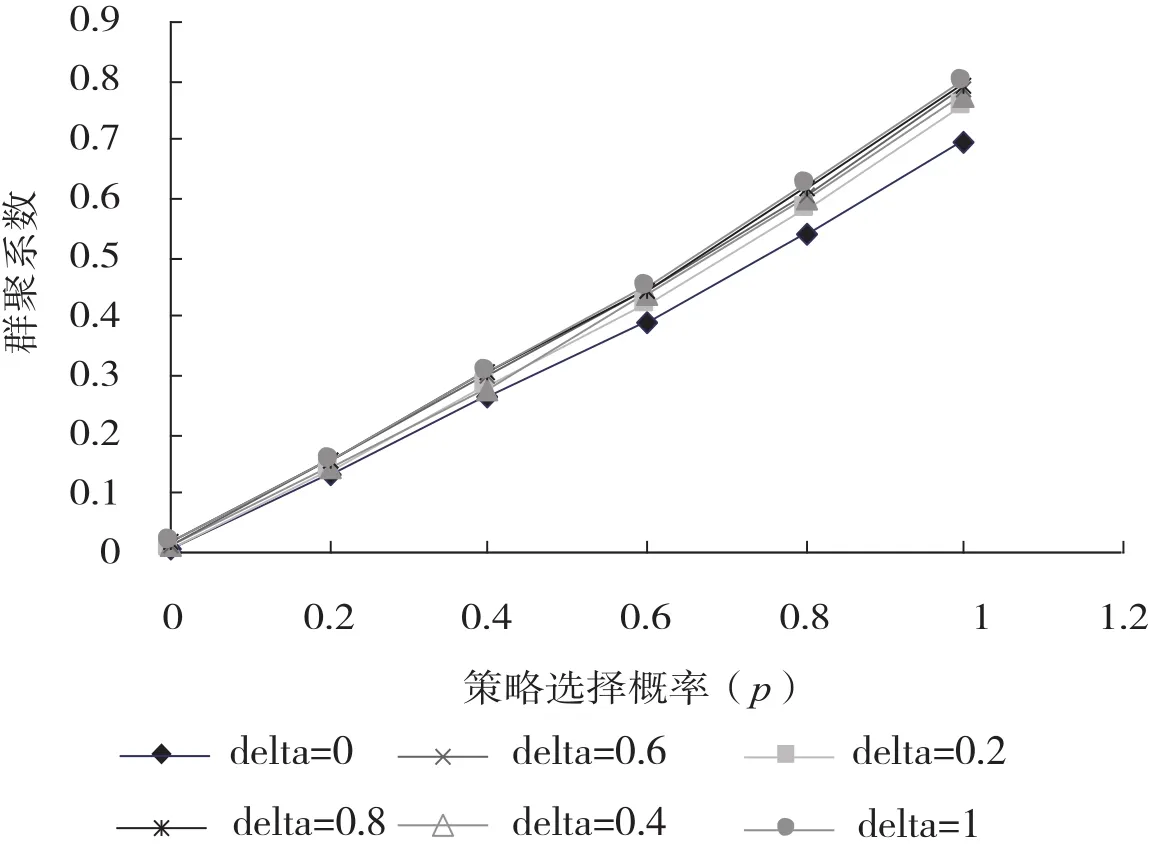
图6 不同效用传递系数(δ)值下聚集系数随策略选择概率(p)的变化图

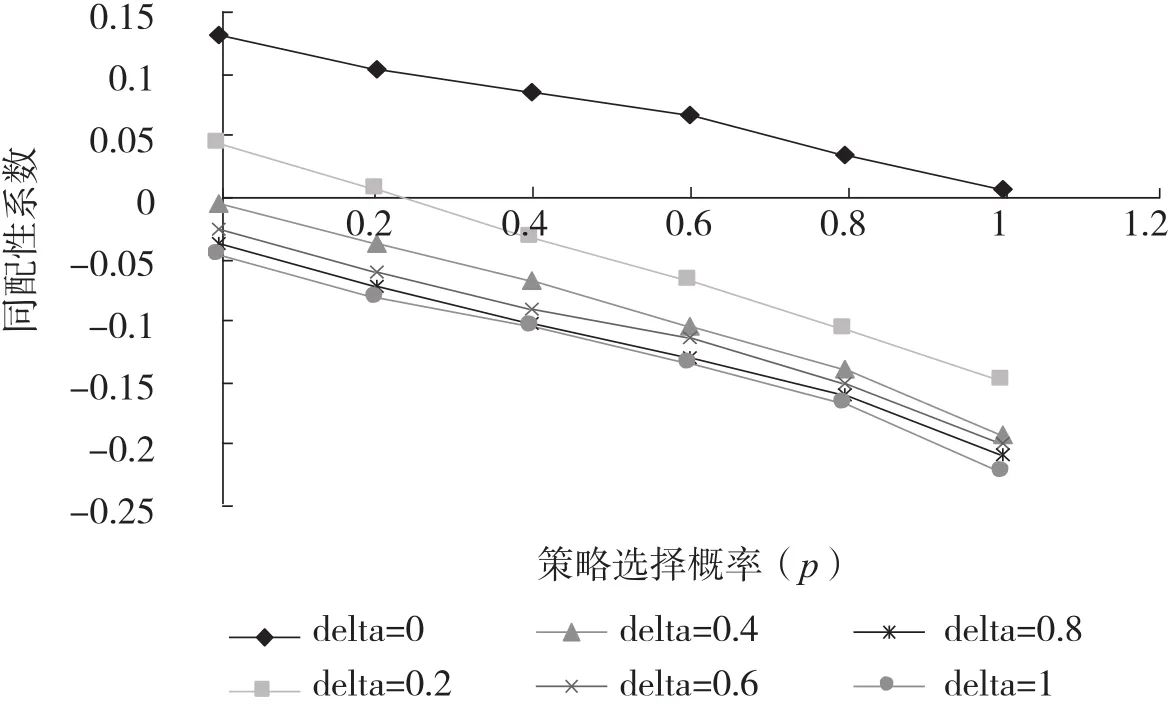
图7 不同效用传递系数(δ)值下同配性系数随策略选择概率(p )的变化图

从以上的数值模拟结果可以看出，当网络中的节点以“效用最大化”和“朋友的朋友”原则作为建边原则时，在参数p、δ位于某个区间时，演化生成的网络将同时具有小世界特性、同配性、层次性、聚集性等特性。同时，可以通过这些参数的调整，来生成同现实数据更为拟合的网络模型。因而，可以用“效用最大化”和“朋友的朋友”原则较全面地解释社会网络的这些结构特性。其中，增长和“效用最大化”原则解释了社会网络特殊的度分布、同配性和小世界特性，而“朋友的朋友”原则解释了社会网络的集聚性。

4 模型在科技人才方面的应用

本文构建的网络模型，在参数p 、δ位于某个区间时，演化生成的网络模型将同时具有小世界特性、同配性、层次性、集聚性等网络结构特性，这些特性经常被应用到科技人才的发现与评价中。

（1）在科技人才发现时，可利用网络的度分布特征与同配性，即度大的节点倾向于与度大的节点连接，将网络中度较大的个体以及与它连接的个体作为科技人才的重点考察对象。如在学术合作者关系网络中，网络中度较大的科技人才及与其有连接的科技人才是网络中的关键节点，都可作为很好的科技人才发现目标。首先，生成一个科技人才合作关系网络，绘制出网络图；再从图中找出度较大的节点，这些节点表示与它合作的人比较多，反映出它的学术影响力或者科研能力较强；最后再找出与其连接的节点，根据同配性可知，该节点也具有较强的学术科研能力。这样就完成了科技人才的发现。

（2）在对科技人才进行评价时，同样可以先生成科技人才合作网络，可以利用网络的层次性对科技人才进行从上到下的评价；利用网络的集聚性对以个体科技人才为中心形成的科技人才研发合作网络进行团队的整体评价。利用同配性来评价某个节点时，比如评价科研能力，可以得出与其连接的节点具有同样的科研能力结论。

5 结论

本文基于组织行为学中的“复杂人”假设，从社会网络中成员的“效用最大化”和“朋友的朋友”择友策略出发，构建了一个参数可调的增长社会网络模型。通过采用计算机仿真的方法进行几十万次的模拟实验，并将得到的数据与现实网络进行比较验证表明，该模型生成的网络所具有的结构特性可以同现实社会网络拟合。该模型的创立，可以帮助我们了解复杂社会网络形成的机理，进一步认识社会网络中的一些参数可能对网络拓扑结构造成的影响。今后更深一步的研究将是采集大量的数据，用实证调研的方法将理论模型的结果与实证研究进行比较，进一步判断该模型的适用性和正确性。

[1] Albert R, Barabasi A L. Statistical Mechanics of Complex Networks[J]. Reviews of Modern Physics, 2002, 74(1):47-36.

[2] Boccaletti S, Latora V, Moreno Y. Complex Networks: Structure and Dynamics[J]. Physics Reports, 2006,424: 175-308.

[3] Jackson MO, Rogers BW. Meeting Strangers and Friends of Friends: How Random Are Social Networks[J]. American Economic Review, 2007,97(3): 890-915.

[4] Watts D, Strogatz S. Collective Dynamics of‘Smallworld’Networks[J]. Nature, 1998,393:440-442.

[5] Barabási A, Albert R. Emergence of Scaling in Random Networks[J]. Science, 1999,286:509-512.

[6] Newman M. Assortative Mixing in Networks[J]. Physical Review Letters, 2002,89(20):208701.

[7] Ravasz E, Barabási A. Hierarchical Organization in Complex Networks[J]. Physical Review E, 2003,67: 1232-1237.

[8] Jackson MO, Wolinsky A. A Strategic Model of Social and Economic Networks[J]. Journal of Economic Theory, 1996,71(1):44-74.

[9] Toivonen R, Onnela JP, Saramäki J. A Model for Social Networks[J]. Physica A, 2006,371(2):851-860.

[10] Kossinets G, Watts DJ. Empirical Analysis of an Evolving Social Network[J]. Science, 2006,311:88-90.

[11] Boguńá M, Pastor-Satorras R. Models of Social Networks Based on Social Distance Attachment[J]. Physical Review E, 2004,70(5):056122.

[12] MEJ Newman, DJ Watts, SH Strogatz. Random Graph Models of Social Networks[J]. Proc Natl Acad Sci USA, 2002,99:2566-2572.

[13] Adamic L, Huberman B. Growth Dynamics of the World Wide Web[J]. Nature, 1999,401:131-133.

Model of Growing Social Network Based on Hypothesis of “Complicated Agent”

Wang Jinping, Gao Yujing, Wang Dehua
(Shandong Vocational College of Science & Technology, Weifang 261053)

Based on the hypothesis of “complicated agent” in organization behavior, proposed two addedge mechanisms in social networks: “utility maximization” and “friends of friends”. Following these two mechanisms, proposed a growing network model. Theoretic analyses and simulation results indicate that the structural characteristics such as degree distribution, clustering, assortativity, hierarchy of the model fit the measured data of the real-world social networks well. The model can help us study the mechanism of social network’s formation.

social networks, structural characteristics, utility maximization, friends of friends, complicated network

O411.3；O242.1

A

10.3772/j.issn.1674-1544.2014.03.014

王金平*（1968- ），女，硕士，山东科技职业学院教授，研究方向：应用数学。高玉静（1983- ），女，山东科技职业学院讲师，研究方向：微分方程。王德华（1985- ），男，山东科技职业学院讲师，研究方向：无网格法。

2013年11月5日。