基于UG的减振弹簧有限元分析

崔联合

(江阴职业技术学院，江苏 江阴 214405)

基于UG的减振弹簧有限元分析

崔联合

(江阴职业技术学院，江苏 江阴 214405)

在理论计算的基础上，采用UG软件建立减振弹簧模型，结合理论值对弹簧模型进行有限元分析，从分析结果可知：模型刚度有限元分析结果与理论计算值基本一致；对弹簧的疲劳强度分析可知，理论疲劳安全系数与有限元分析结果基本相等，模型的强度足够；弹簧静强度安全系数为1.42，静强度合格；弹簧最小固有频率大于振动机振动频率，故弹簧不会发生共振。

UG; 减振弹簧; 有限元; 刚度; 疲劳强度

0 前言

热熔断体鼓簧振动筛是用来实现鼓簧能自动装配于热熔断外壳内的一台重要设备，振动筛减振弹簧的主要作用是支撑振动筛机体, 使机体实现所需要的振动, 并保证鼓簧在振动电机激振力的作用下，通过振动筛筛孔均匀、准确地落入热熔断体铝合金壳内。同时，减振弹簧还起着减小振动电机传给基础或结构架动载荷的作用。振动筛工作时, 减振弹簧的刚度、质量、自由高度和自振频率等参数均会影响振动筛筛网的振幅、效率及振动轨迹, 从而直接影响热熔断体鼓簧安装的效果和效率。因此弹簧的强度、刚度和共振等特性已成为专业人员研究的重点[2-5]。文章根据减振弹簧实际工况进行弹簧理论设计计算，采用UG软件对弹簧建模并对减振弹簧进行刚度、疲劳强度、静强度和共振有限元分析与研究，以期对减振弹簧各项理论计算值进行校验，获得最优解，减少设计误差。

1 弹簧基本参数确定与计算

根据减振弹簧工作状况，螺旋弹簧上端安装振动筛，下端固定于支架上，承受交变轴向力，已知弹簧受到的最小工作载荷F1=100N，最大工作载荷F2=300N，工作行程h为8mm。振动筛弹簧属于I类负荷弹簧，受循环载荷作用次数在1×106次以上。弹簧两端并紧且磨平，支承圈数为2圈。振动电机转速ω=105rad/s。

1) 材料选择

根据振动筛工作情况，初选弹簧中径D2=25mm，材料选用40Cr，用UG库材料AISI_STEEL_4340代替，该材料切变模量G=80.8×103N/mm2，弹性模量E=193×103N/mm2，泊松比为0.284，密度ρ=7.85e-006kg/mm3，抗拉强度σb=1420MPa，疲劳强度系数为1917MPa，疲劳强度指数为-0.099，疲劳韧性系数为1.122，疲劳韧性指数为-0.72。

2) 弹簧参数计算

估取弹簧直径为4mm，由文献[1]参照碳素弹簧钢丝抗拉极限强度，取弹簧丝σb=1420MPa，当循环载荷作用次数N=106时，则弹簧许用应力τp=0.3σb=0.3×1420=426MPa

初定旋绕比C和曲度系数K，根据公式：

(1)

查文献[1]取C=6.6,K=1.227。

弹簧丝直径：

d=D2/C=25/6.6=3.79mm

(2)

式中：C为旋绕比；D2为弹簧中径。根据文献[1]取d=4mm。

确定旋绕比C：

C=D2/d=25/4=6.25

(3)

确定曲度系数K由公式：

(4)

式中：C为旋绕比。

由F1，F2求弹簧刚度：

(5)

式中：f1为最小工作载荷下的变形量；f2为最大工作载荷下的变形量；F1为最小工作载荷，F2为最大工作载荷。

最小工作载荷下的变形量：

f1=F1/k=100/25=4mm

(6)

最大工作载荷下的变形量：

f2=F2/k=300/25=12mm

(7)

式中：F1为最小工作载荷，F2为最大工作载荷；k为弹簧刚度。

压并时变形量Fb取全变形量的65% 则：

Fb=f2/0.65=12/0.65=18.5mm

(8)

式中：f2为最大工作载荷下弹簧的变形量。

弹簧有效圈数：

(9)

式中：G为材料切变模量；d为弹簧丝直径；f2为最大工作载荷下弹簧的变形量；F2为最大工作载荷；D2为弹簧中径。

按文献[1]取弹簧有效圈数n=7，弹簧总圈数。

n1=n+2=9

(10)

式中：n为弹簧有效圈数。

压并高度：

(11)

式中：n为弹簧有效圈数；d为弹簧丝直径。

弹簧自由高：

H0=Hb+Fb=34+18.5=52.5mm

(12)

式中：Hb为压并高度；Fb为压并时变形量。

按文献[1]取H0=55mm。

节距p：

p=(H0-1.5d)/n=(55-1.5×4)/7=7mm

(13)

式中：H0为弹簧自由高度；d为弹簧丝直径；n为弹簧有效圈数。

3) 验算

a) 稳定性

高径比：

b=H0/D2=55/25=2.2﹤5.3 满足要求。

(14)

式中：H0为弹簧自由高度；D2为弹簧中径。

b) 疲劳强度

最小切应力：

(15)

最大切应力：

(16)

式中：F1最小工作载荷；F2最大工作载荷；D2为弹簧中径；K为曲度系数；d为弹簧丝直径。

根据文献[1]，当循环载荷作用次数N=106时：

τ0=0.33σb=0.33×1420=468.6MPa。

(17)

式中：σb为弹簧丝抗拉强度。

疲劳安全系数：

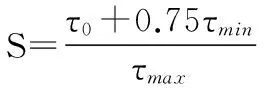
(18)

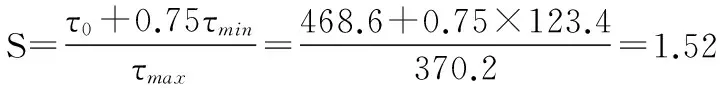
式中：τ0为脉动疲劳极限；τmin最小切应力；τmax最大切应力；Sp为许用安全系数, 当弹簧的设计计算及材料数据精确性较高时, 取Sp= 1. 3～1.7。

c) 静强度

取脉动疲劳极限：

τs=0.42σb=0.42×1420=596.4MPa

(19)

式中：σb为弹簧丝抗拉强度。

静强度安全系数：

Ss=τs/τmax=596.4/370.2=1.61，满足要求。

(20)

式中：τs为脉动疲劳极限；τmax最大切应力。

d) 共振验算

弹簧自振频率：

(21)

式中：d为弹簧丝直径；n为弹簧有效圈数；D2为弹簧中径。

而强迫机械振动频率为：

(22)

式中：ω为振动电机转速。

fn/fr=325.5/16.7=19.5>10 满足要求。

(23)

2 减振弹簧有限元分析

2.1 刚度分析

为了确保应力计算的精确性, 采用三维实体单元进行网格化分，单元类型为CTETRA(10), 单元大小为2mm，模型共计26179个节点, 13147个单元。弹簧工作时, 在上支承圈平面上承受轴向交变载荷, 因此, 在下支承圈平面上施加固定约束, 在上支承圈平面上施加轴向强迫位移。图3为减振弹簧三维模型，图4为减振弹簧的有限元模型。

图3 减振弹簧三维模型

图4 减振弹簧有限元模型

图5为本例模型在施加轴向交变载荷所得到的弹簧位移云图，从图中可知，此时最大位移为9.738e+000mm；图6为弹簧在此工况下，节点所受到的约束反力，从图6可知，x、y、z向节点最大反作用力Fxmax=-1.065e+001N，Fymax=6.294e+001N，Fzmax=-2.763e+001N, 则弹簧刚度为27.63N/mm，该值与由式(5)计算得到的理论刚度值25N/mm接近。

图5 减振弹簧位移云图

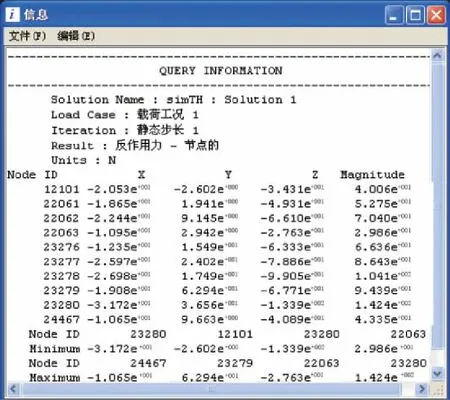
图6 轴向强迫位移下弹簧的约束反力

2.2 疲劳强度分析

由于热熔断体鼓簧振动筛在实际生产中，通常为24h连续作业的，所以振动筛的破坏形式主要是减振弹簧的疲劳断裂，因此对减振弹簧进行疲劳强度分析是有现实意义的。

在UG创建耐久性解算方案中，应力安全因子的应力准则选取为强度极限；疲劳安全因子的设计寿命准则确认为无限寿命，疲劳强度因子Kf取1；疲劳寿命准则选取Smith_Watson_Topper。在疲劳载荷变化参数设定中，取缩放函数为完整单位周期，循环次数取1e6，缩放因子取1。图7为弹簧模型在疲劳工况下的强度安全因子云图，从图7可以看到，单元上SSF值最小为1.069e+000，最大为5.036e+007，这说明此模型的强度是足够的。图8为模型在疲劳工况下的疲劳安全因子云图，从图8可知，在弹簧支承圈内则区域单元上的FSF值最小为1.731e-002，这说明在这些部位弹簧易出现疲劳裂纹或失效；图9为模型在疲劳工况下的疲劳寿命云图，从图9可以看到，在弹簧支承圈与有效圈数过渡处寿命最小为1.000e+000，这表明了在弹簧的这些区域容易发生破坏。

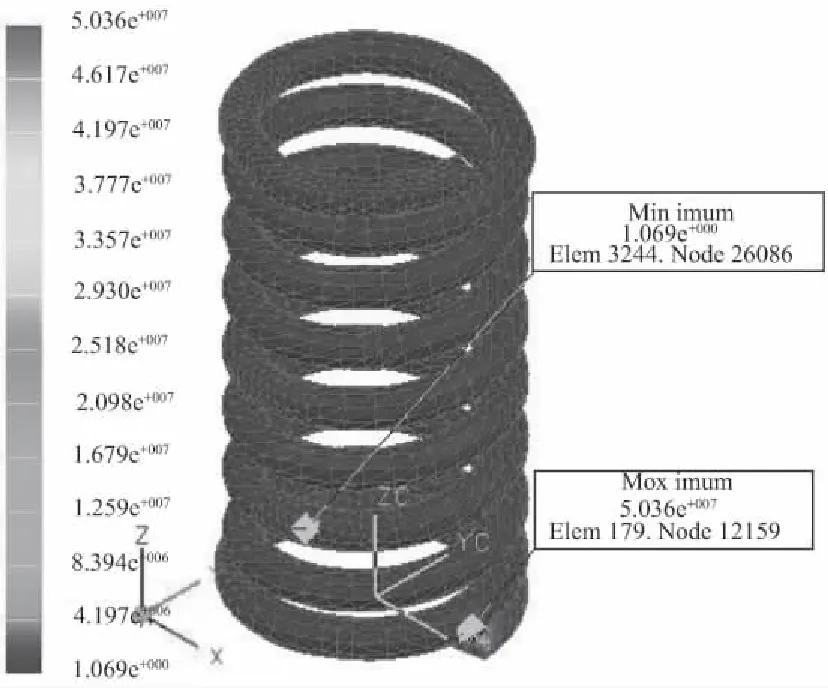
图7 强度安全因子云图

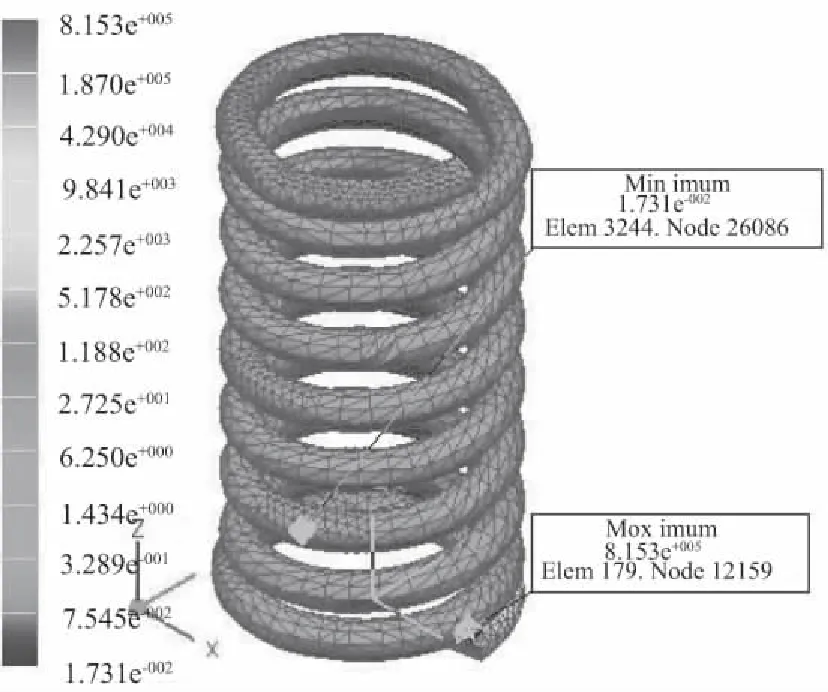
图8 疲劳安全因子云图

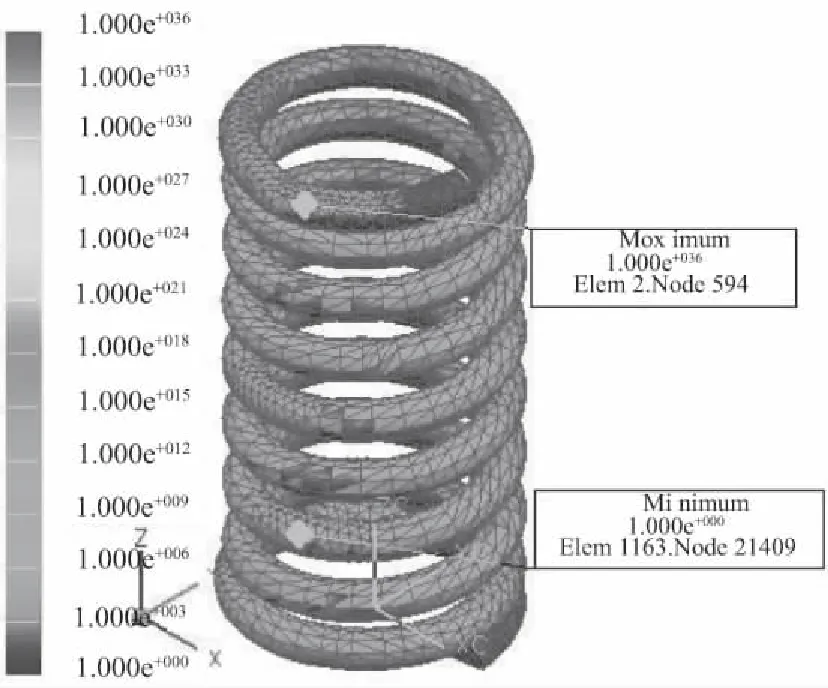
图9 疲劳寿命云图

2.3 静强度分析

图10为减振弹簧受到交变轴向压力时的Von-Mises应力云图，由图10可知, 弹簧的最大应力为4.206e+002MPa，发生在第一支承圈的内侧。该弹簧材料为40Cr钢, 由GB4537-1989可知其强度极限为1420MPa , 则安全系数为1.42 , 可见该弹簧静强度合格。

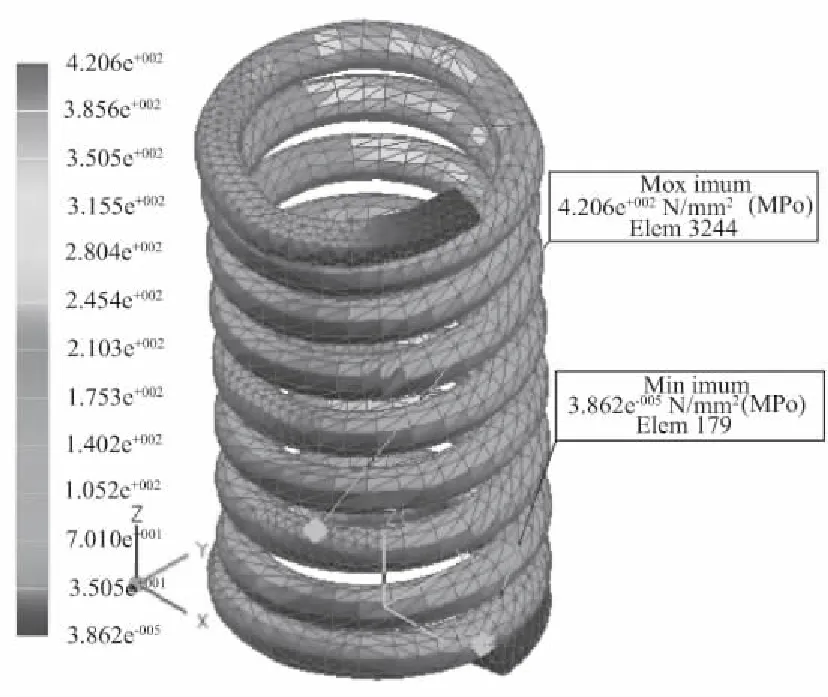
图10 减振弹簧Von-Mises应力云图

2.4 共振分析

热熔断体鼓簧振动机在工作时，振动源及减振弹簧运行的平稳性对鼓簧筛选的效率具有重要影响，因此要对弹簧的动态特性(即弹簧自身的固有频率与激励频率)进行必要的分析与研究。对弹簧进行动力学有限元分析，可了解弹簧的动态性能，对设计与计算弹簧具有一定的参考价值。模态分析时，在弹簧支承圈下平面上约束弹簧的全部刚体位移, 分析并得到弹簧前4 阶固有频率和振型, 表1为模型计算结果，从表中可知，模型最大固有频率为1.432e+002Hz，最小固有频率为6.008e+001Hz, 该值大于振动机强迫机械振动频率16.7Hz , 故弹簧不会发生共振。图11 为模态下幅值位移云图, 从表1及图11可知，一阶振动节点x向最大位移为6.869e+000mm，最大幅值位移为7.351e+000mm，模型振型主要为横向变形; 二阶振动节点y最小位移为-6.867e+000mm，z向为-2.157e+000mm，最大幅值位移为7.291e+000mm，模型振型为横向和轴向耦合变形; 三阶振动z向节点最大位移为-5.691e+000mm，最大幅值位移为5.722e+000mm，其振型为轴向变形; 四阶振动x向最小位移为-6.564e+000mm，最大为-3.689e+000mm ，y向最大位移为5.210e+000mm，y向最小位移为-5.420e+000mm，z向位移量较小，幅值位移在6.557e+000mm到6.594e+000mm之间波动，模型振型主要为扭转变形[3]。

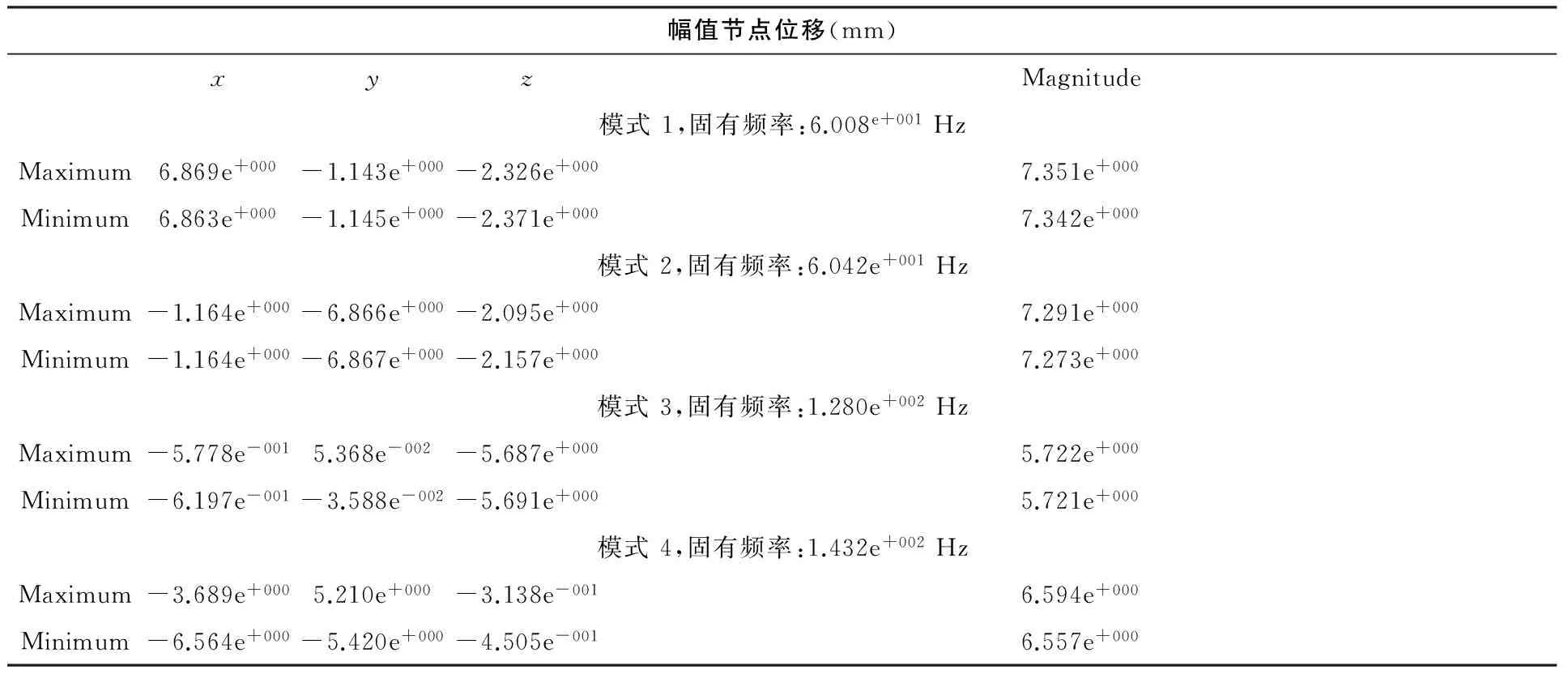
表1 模型计算结果

(a)一阶振动

(b)二阶振动

(c)三阶振动

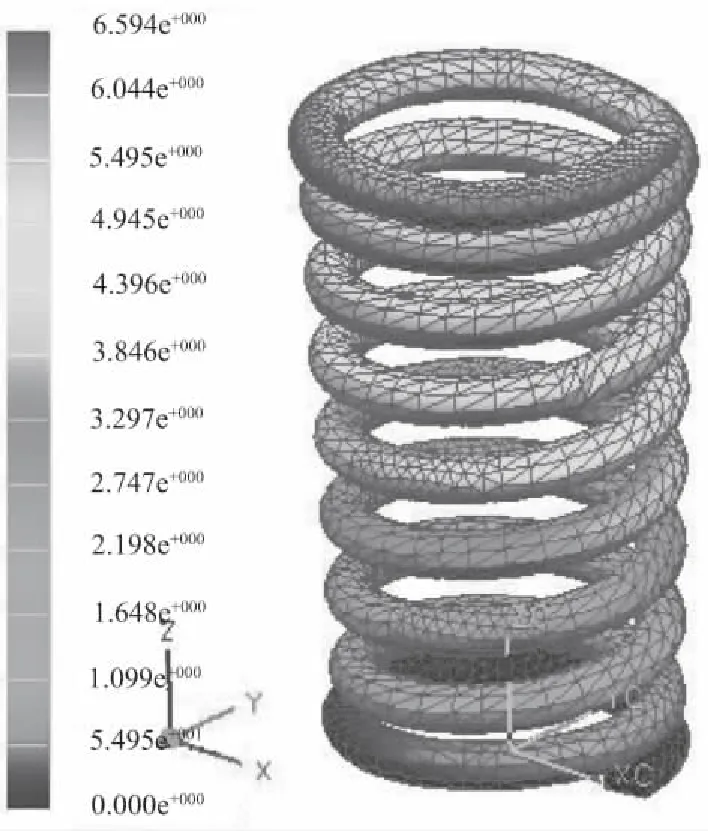
(d)四阶振动图11 模态下幅值位移云图

3 结论

在理论计算的基础上，建立减振弹簧模型，结合理论值对弹簧模型进行有限元分析，从分析结果得出以下结论：

1) 模型刚度有限元分析结果与理论计算值基本一致；

2) 从对弹簧的疲劳强度分析可知，理论疲劳安全系数与有限元分析结果基本相等，模型的强度足够；

3) 弹簧静强度安全系数为1.42 ，静强度合格；

4) 弹簧最小固有频率大于振动机振动频率，故弹簧不会发生共振。

[1] 成大先.机械设计手册[M].北京:化学工业出版社,2008.

[2] 李红艳.基于ANSYS的圆柱螺旋弹簧的强度与疲劳寿命分析[J].机械设计与制造,2010,10:92-93.

[3] 商跃进,曹茹,戴蓉. 圆柱压缩螺旋弹簧三维静动态有限元分析与寿命预测[J].中国农机化,2008,2:75-78.

[4] 钟文彬.圆柱螺旋弹簧刚度特性的有限元分析[J]. 机械, 2011, 38 (12):21-23.

[5] 范俊,米彩盈. 基于子模型技术的螺旋弹簧应力分布的有限元分析[J]. 机械, 2010, 37 (9):22-24.

Finite Element Analysis of Damping Spring Based on UG

CUI Lian-he

(JiangyinPolytechnic College, Jiangyin 214405, China)

The model of damping spring is built by UG software on the basis of theoretical calculation, and the finite element analysis of damping spring is processed, in combination with the theoretical values. In analysis result, it can be found out that the theoretical value of the model stiffness is the same with that of the finite element analysis; the theoretical fatigue safety factor is basically identical with that of the finite element analysis, and the model strength is enough; the static strength safety factor of the spring is 1.42, which meets the requirement of the static strength; the smallest natural frequency of the damping spring is bigger than the vibration frequency of the vibrating machine, so the spring does not resonate at a certain frequency.

UG; damping spring; finite element; stiffness; fatigue strength

崔联合(1968-)，男，安徽铜陵人，副教授，工学硕士，主要从事材料成形及机械制造等方面的科研和教学工作。

TB115.1

A

1671-5276(2014)02-0139-05

2013-01-16