基于ARCH模型簇的路径行程时间可靠性分析
2014-07-18李玮峰段征宇郭高华
李玮峰,段征宇,郭高华
(同济大学道路与交通工程教育部重点实验室,上海200092)
基于ARCH模型簇的路径行程时间可靠性分析
李玮峰,段征宇*,郭高华
(同济大学道路与交通工程教育部重点实验室,上海200092)
行程时间可靠性是反映道路交通网络可靠性的重要指标.由于交通系统存在不确定性,行程时间的波动具有异方差性,利用传统数理统计方法建立的行程时间预测模型,无法对行程时间进行准确的预测.针对行程时间波动的尖峰厚尾、集群性等特点,引入计量经济学中的ARCH模型簇.通过实证分析,评价行程时间波动的时变性、持续性,描述系统外部信息冲击的分布,分析行程时间波动对外部信息冲击的反应机制.结果表明,ARCH模型簇能很好地适应行程时间序列数据的方差变化特点,与交通系统的自身特性相吻合,能够对路径行程时间的可靠性进行有效的评价.
交通工程;可靠性;ARCH模型簇;行程时间;时间序列
1 引言
行程时间反映了从起点到目的地的出行成本.由于受到交通需求随机性变化及道路交通实际运行状况的影响,路网中的路径行程时间变化具有时变性、随机性和不确定性,且表现出复杂的波动特性[1].
在现有的大量研究中,利用数理统计方法建立行程时间的预测模型,主要方法包括:历史平均模型、线性回归模型、时间序列模型、卡尔曼滤波模型、马尔可夫预测模型、极大似然估计模型等[2].然而,交通系统是一个服从一定概率分布的随机过程,行程时间的波动则是这个随机数据生成过程的实现.交通系统的不确定性,使得路径行程时间变化的时间序列在数值变化规律上具有一些独特的特征,主要表现为行程时间变化的异方差性.异方差性违反了线性回归模型关于同方差性的假设,也使得常规的时间序列分析方法(如ARMA模型等)不再适用,模型得到的参数估计量不再有效,基于模型得到的行程时间预测值也会产生偏差.
本文基于路径行程时间波动的尖峰厚尾、集群性等特性,引入计量经济学中的ARCH模型簇(Autoregressive Conditional Heteroskedasticity Model,自回归条件异方差模型),利用模型参数从不同的角度对路径行程时间的可靠性进行评价.通过模型,既对路径行程时间波动的时变性、持续性进行评价,也对系统外部信息的分布进行描述,并分析了路径行程时间波动对外部信息冲击的反应机制.
2 问题描述与模型建立
2.1 研究对象与研究数据
为了研究路径行程时间的可靠性,综合考虑数据质量、路段长度、交通控制与管理等因素,在上海市快速路系统中选择了5条路径作为研究路径,如图1所示.利用采集于研究路径上的浮动车数据,估算得到各路径在不同时段的行程时间;将计算得到的路径行程时间,按照时间顺序依次排列,即得到路径行程时间的时间序列,从而为后续的建模与分析提供基础数据.

图1 研究对象Fig.1 Study objects
本文使用的浮动车数据,采集于2010年5月5日至5月11日,更新周期为两分钟.利用浮动车数据计算得到路段行程时间,以及与之匹配的道路路段长度,路径行程时间的计算公式为式中表示路径i在t时刻的路径行程时间;Ii表示组成路径i的路段集合;lj表示路段j的长度表示路段j的路段平均行驶速度.

2.2 行程时间波动特性分析
行程时间序列本身是一个非稳定的时间序列,但是,李玮峰等[3]的研究表明,在对行程时间序列进行对数化处理后,所得到的时间序列是一个一阶单整序列.也就是说,对数化处理后的行程时间序列,其一阶差分序列是一个稳定的时间序列.利用该序列进行统计分析,能够消除回归模型中随机误差项的异方差性,减少不确定性因素的干扰,从而保证分析结果具有良好的统计特性.
参考经济学中对收益率等的定义,将行程时间对数值的一阶差分定义为行程时间的波动率,即
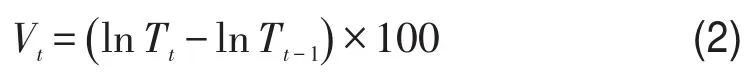
式中Tt为t时刻的路径行程时间.
以第1条路径为例,其行程时间波动率序列Vt和均方波动率序列分别如图2(1)和图2(2)所示.和分别表示行程时间波动率围绕其均值水平的双向波动和均方波动.对于这两个序列的进一步分析,可以得到行程时间波动的一系列特征.
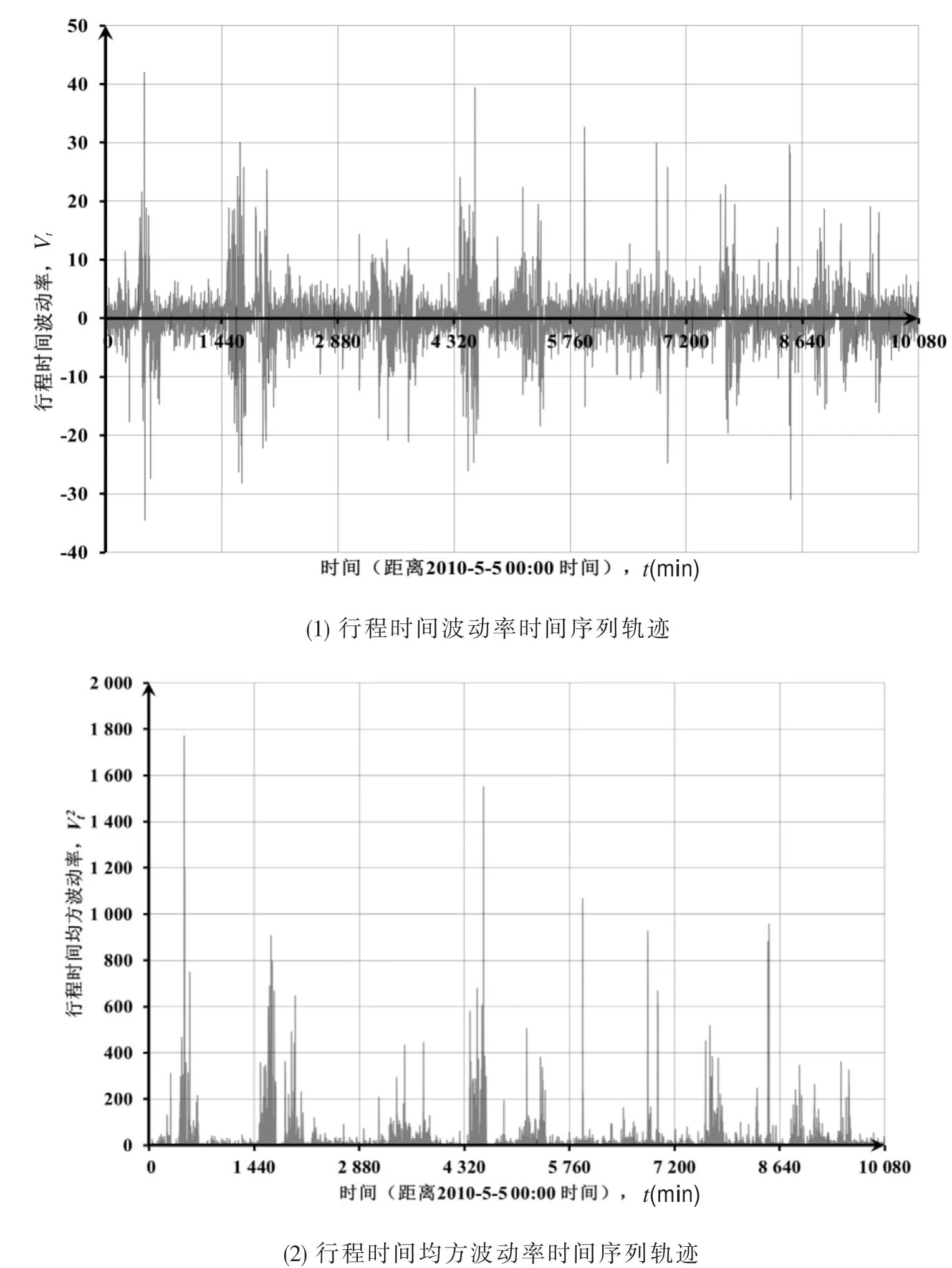
图2 第1条路径的行程时间波动率序列Fig.2 Series of travel time volatility of Route 1
特征一:集群性.
图2(1)和图2(2)中,时间序列的变化轨迹均出现了多个异常的峰值,行程时间波动率的变化在某一时间段内持续偏高或持续偏低,在序列方差变化过程中,幅度较大的变化相对地集中在某些时段内,而幅度较小的变化也会集中在另外一些时段内.行程时间波动率的波动表现出以某种相似特征集群出现的现象,说明行程时间波动率具有集群性的特点.另外,行程时间波动的集群性特征,也表明其具有异方差性.
特征二:尖峰厚尾
进一步计算路径行程时间波动率的统计特征值,包括平均波动率(均值)、标准差、偏度、峰度、Jarque-Bera统计量等,根据统计量的数值特征,对行程时间的波动特性进行分析.各统计量的定义如式(3)~式(7)所示.
平均波动率(均值)

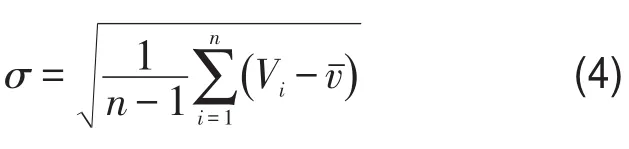
偏度

峰度
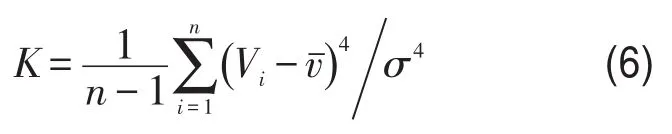
Jarque-Beta统计量

式(3)~式(7)中,n为样本容量;式(7)中,k为自由度.各统计量中,Jarque-Bera统计量是用来检验一组样本能否认为来自正态分布总体的统计量.
各路径行程时间波动率序列的统计量计算结果如表1所示,可以得到以下结论:
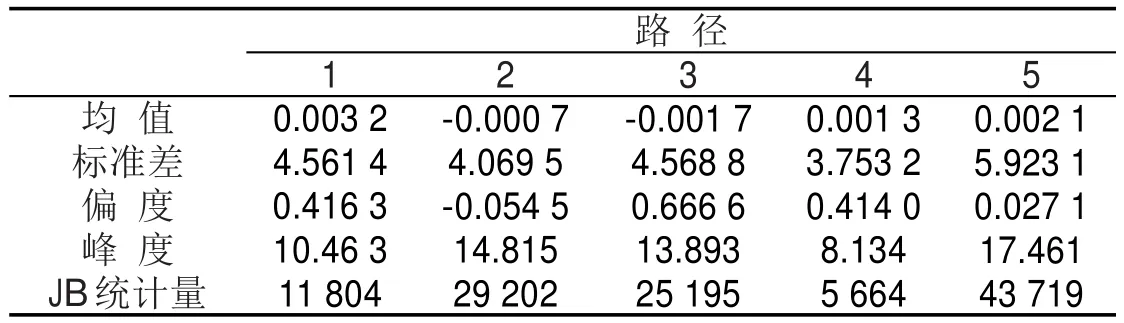
表1 行程时间波动率序列统计量计算结果Table 1 Statistics of travel time volatility series
(1)五条路径的行程时间波动率序列均值都在0上下浮动,说明其均值为常数;
(2)五条研究路径中,仅第2条路径的偏度值略小于0,说明除了第2条路径的波动率序列具有不太明显的左偏情况,其余各条路径均具有右偏的特性,即有较长的右拖尾;
(3)五条路径的峰度均远远大于3,说明行程时间波动率相较于正态分布而言,形态更为陡峭,其中第2条路径的凸起程度最为明显;
(4)五条路径的JB统计量数值都非常大,说明波动率序列均不服从正态分布.
由此,可以认为行程时间波动率具有尖峰厚尾的特性,即与正态分布相比,会呈现出更高的峰度和更厚的尾部,在统计量的数值上表现为不等于0的偏度,以及大于3的峰度.
2.3 ARCH模型簇
ARCH模型是恩格尔[4]在1982年基于对时间序列数据波动的集群性,以及分布的厚尾特点等的考虑提出的.从时间序列的统计特性角度而言,ARCH模型对于行程时间波动率的分析具有较好的适用性.ARCH模型的基本思想是指在以前信息集下,某一时刻噪声的发生服从正态分布.该正态分布的均值为零,方差是一个随时间变化的量,即条件异方差;并且这个随时间变化的方差是过去有限项噪声值平方的线性组合,即为自回归.一个完整的ARCH() q模型可以表示为

式中yt是一组时间序列数据;x2t,x3t,…,xnt是解
在ARCH模型中,条件方差方程中的滞后阶数有可能过大,在有限样本的情况下会带来计算效率与精度上的缺陷,条件方差方程中系数非负的约束也很难满足.因此,Bollerslev[5]、Glosten[6]及Nelson[7]等人分别在ARCH模型的基础上进行改进,得到了GARCH模型(Generalized Autoregressive Conditional Heteroskedasticity Model,广义自回归条件异方差模型)、TARCH模型(Threshold ARCH Model,门限自回归条件异方差模型)及EGARCH模型(Exponential GARCH Model,指数广义自回归条件异方差模型).
GARCH模型.
GARCH() p,q模型的条件方差公式为
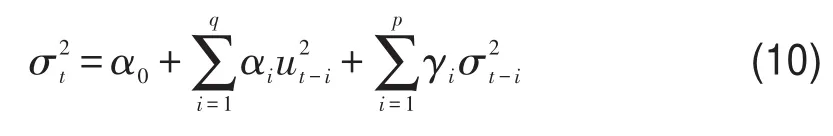
式中p为条件方差的滞后期数;q为残差项的滞后期数.
GARCH模型既考虑了上期的预测方差,也考虑了前期观测到的波动信息,并通过常数项对长期均值进行了加权平均,兼顾了时间序列波动的长期平衡和阶段性的短期变化,可以很好地刻画时间序列波动的长期平衡和阶段性的短期变化.
TARCH模型.
TARCH模型在GARCH模型的基础上,引入了非对称变量,其条件方差公式为

式中It是一个虚拟变量,若ut<0,则It=1,其余情况It=0.
在经济学中,定义收益率出现非预期性增加表示市场出现“利好消息”,而收益率上的非预期降低表示市场出现“利空消息”.若利空消息引起资产的波动与利好消息引起的资产波动不一致,则表明存在非对称效应.在TARCH模型中,当ut>0(利好消息)时,有一个α1的冲击,当ut<0(利空消息)时,有一个α1+θ的冲击.若θ显著不等于0,则表明存在非对称效应.
EGARCH模型.
EGARCH模型是在考虑非对称影响的同时,将其看作指数形式,其条件方差公式为
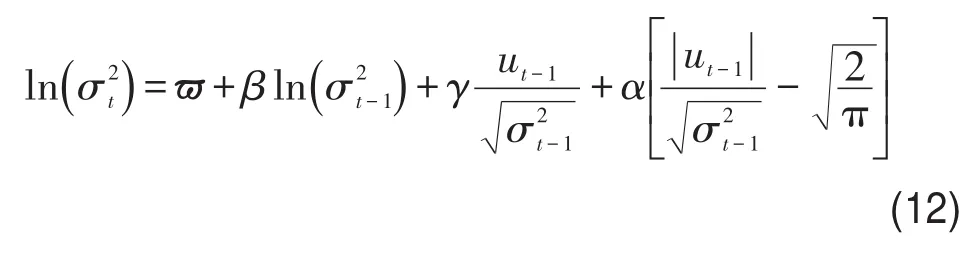
本文主要利用GARCH() 1,1模型、TARCH模型,以及EGARCH模型对行程时间波动率序列进行建模.
3 基于ARCH模型簇的行程时间可靠性分析
根据式(8)~式(12),建立了各条研究路径的GARCH(1,1)方程、TARCH方程及EGARCH方程.利用EVIEWS软件分别对各方程的参数进行估计,结果如表2所示.

表2 ARCH模型簇参数估计Table 2 Factors of ARCH model cluster
根据表2数据,将从路径行程时间波动的时变性、波动的持续性、系统新信息冲击的分布、系统对外部新信息的反应等角度,根据不同的参数指标对各条研究路径的行程时间可靠性进行分析.
3.1 路径行程时间波动的整体评价
路径行程时间的整体波动,可由波动的时变性进行评价,即通过行程时间波动率序列残差项的异方差性来反映.利用各条路径在EGARCH模型下得到的条件方差序列,对五组波动率序列的波动性进行了比较.
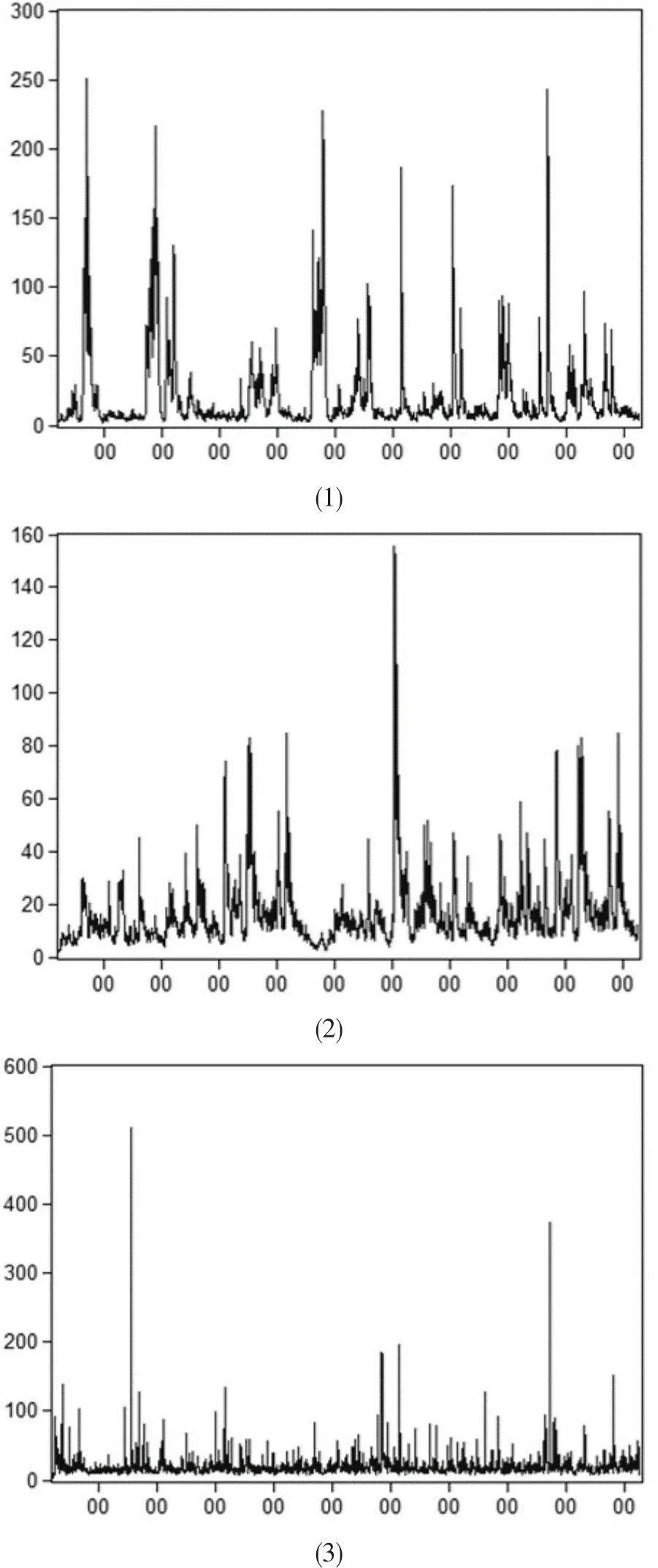
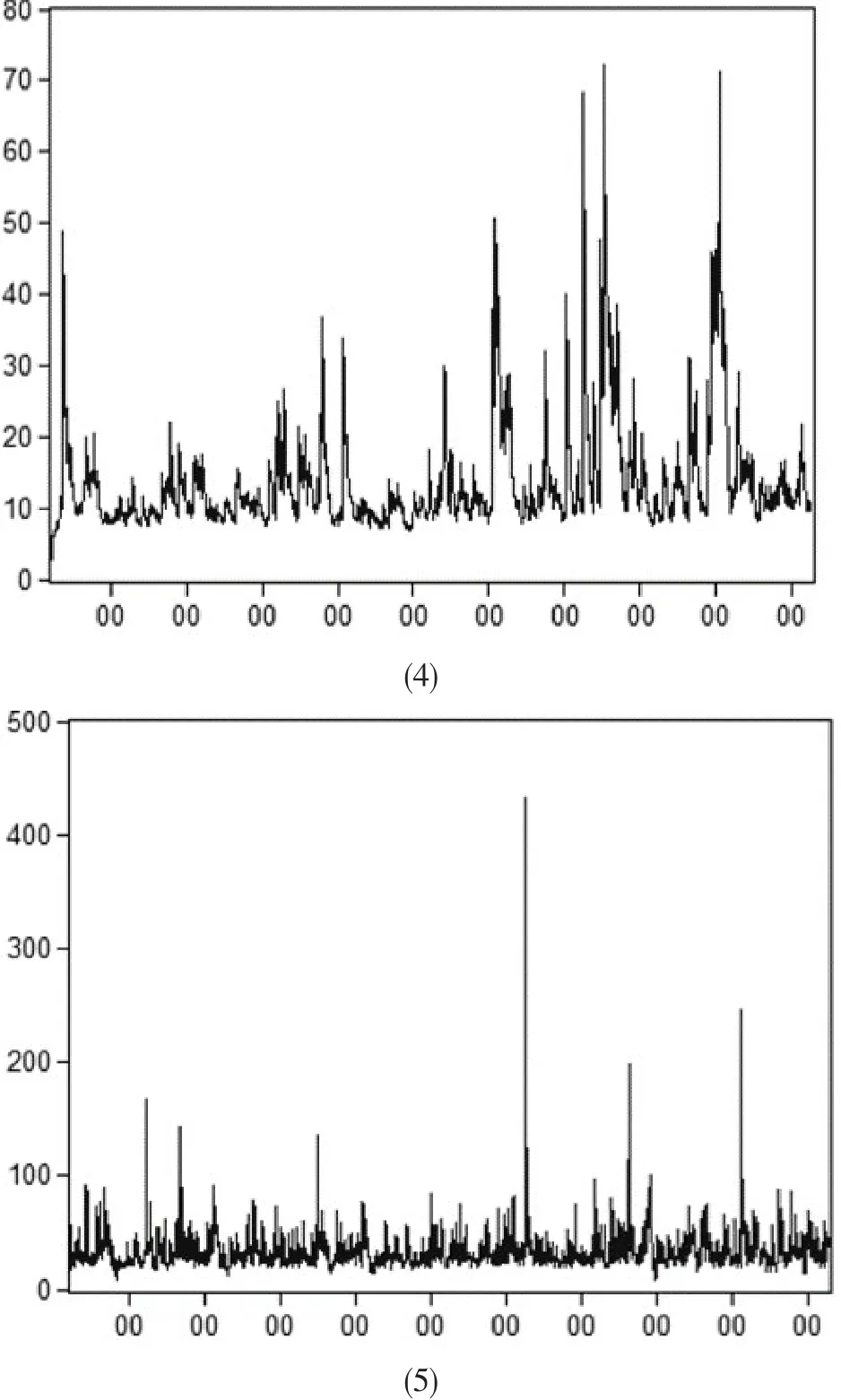
图3 EGARCH模型行程时间波动率条件方差序列Fig.3 Conditional variance series of travel time volatility in EGARCH model
根据图3分析,各条路径的条件方差波动均比较剧烈,且都有异常的峰值.在整个样本区间内,第2、3、5条路径行程时间的波动较另外两条更为剧烈.为了能够更好地刻画各条路径的波动特点,对条件方差序列的统计特征量进行了计算,计算结果如表3所示.
通过比较条件方差序列的算术平均值和中位数,各路径条件方差的大小关系为即第5条路径的行程时间波动最明显,其可靠性最差,而第4条路径的行程时间波动最小,可靠性较高.
3.2 新信息冲击的分布
城市交通系统是一个受环境影响的开放系统,交通问题涉及到人、车、路、环境等之间的复杂关系,系统以外的外部因素干扰,也会对交通系统运行的可靠性产生影响.因此,研究系统外部信息冲击的分布,对评价路径行程时间的可靠性至关重要.
新信息冲击的分布,可以通过EGARCH模将标准化残差序列的分布特征与标准正态分布进行对比,评价新信息冲击分布的密集程度,标准化残差序列的统计特征值如表4所示.型中的标准化残差序列进行评价.通过

表3 条件方差序列统计值Table 3 Statistics of conditional variance series
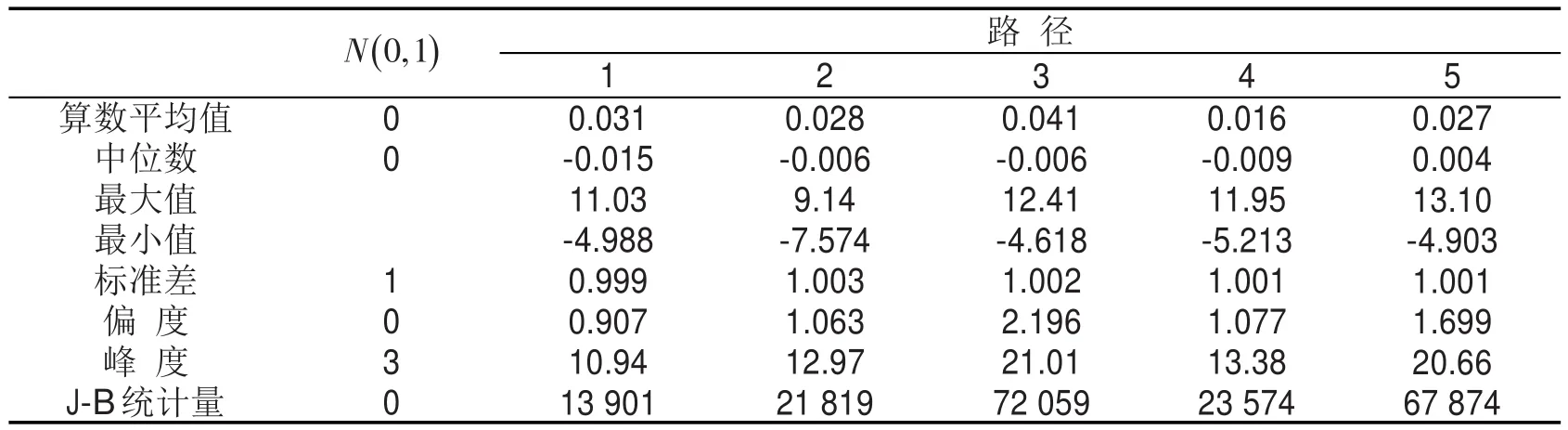
表4 标准化残差序列统计值Table 4 Statistics of standardized residuals series
第3条路径对所应的峰度值最高,第1条路径的峰度最小,说明第3条路径当期新信息的冲击较其他路径而言更为集中和强烈,第1条路径新信息的冲击较为温和.
3.3 路径行程时间对新信息冲击的反应
以日常经验为例,当交通系统出现拥堵,行程时间会产生向上的波动,也就是在交通系统中出现了经济学中的“利好消息”;当拥堵逐渐消散,行程时间向下波动,即出现了“利空消息”.当路径行程时间向不同方向波动时,对行程时间波动的影响亦是不同的,TARCH模型和EGARCH模型中的不对称项系数都可以作为衡量非对称效应程度的尺度.
从参数数值来看,表2中各路径EGARCH模型的γ值,有γ4<γ1<γ2<γ5<γ3,即第4条路径的不对称效应程度最小,而第3条路径的不对称效应程度最大.TARCH模型中各路径均有θ<0,表明各路径行程时间向上波动时,会使行程时间的波动减小,而向下波动时,则会使行程时间的波动增大.
另一方面,利用EGARCH模型中的回归系数α和γ,将标准化残差序列{vt}至lnS=α|v|+γv中,可得不同路径行程时间波动率序列的信息反应曲线,如图4所示.
在图4中,横坐标v是标准信息过程,v<0表示利空消息,v>0表示利好消息,其绝对值大小表示信息冲击的强弱.纵坐标lnS可以表示系统对信息的反应.曲线沿y轴正向的位置越高,说明系统在受到信息冲击后,波动越大.
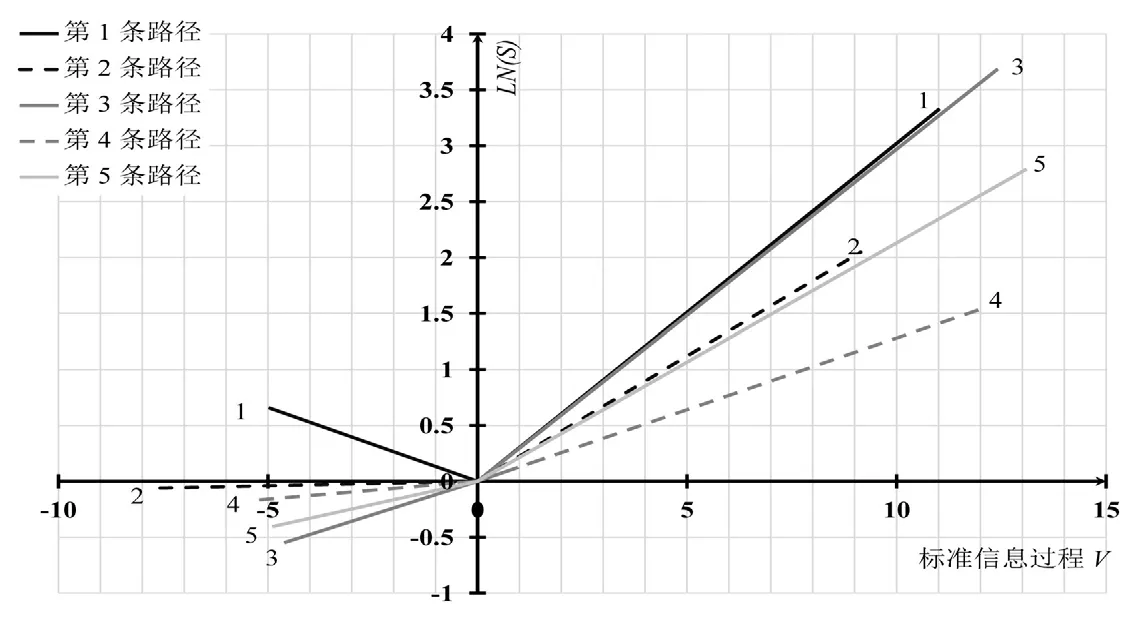
图4 行程时间波动率信息反应曲线Fig.4 Information response curve of travel time volatility
根据图4,五条研究路径行程时间波动率序列的信息反应曲线都具有非常明显的非对称特点,对于所有的路径,对利好消息的反应都比利空消息强烈,表明当路径行程时间向上或向下波动相同程度时,向上波动对行程时间波动产生的影响更大.以第3条研究路径为例,在受到信息冲击时,反映出两个特征,一是对于利空信息,其行程时间波动率的波动性最小,对于利好信息,其吸收信息的能力则较差,其非对称效应程度最大;二是随着信息冲击加强,信息反应曲线与其他曲线的高差逐渐加大,说明其对于冲击程度较大的新信息,吸收能力较差.
3.4 路径行程时间波动的持续性
GARCH模型兼顾了阶段性的波动与平稳,可以用来评价路径行程时间波动的持续性.设参数λ=α1+γ1,利用滞后残差的平方与滞后条件方差系数的和,比较波动率序列波动性的持续性强弱.
根据表2数据对不同路径的λ值进行计算,有λ4<λ5<λ2<λ3<λ1=0.302,表明五条路径的路径行程时间波动均不具有很强的持续性,其中第4条路径波动持续性最小,第1条路径的持续性最强.
4 研究结论
根据ARCH模型簇分析结果,结合行程时间波动率尖峰厚尾的特性,本文对路径行程时间波动率序列的波动特点的总结如表5所示.
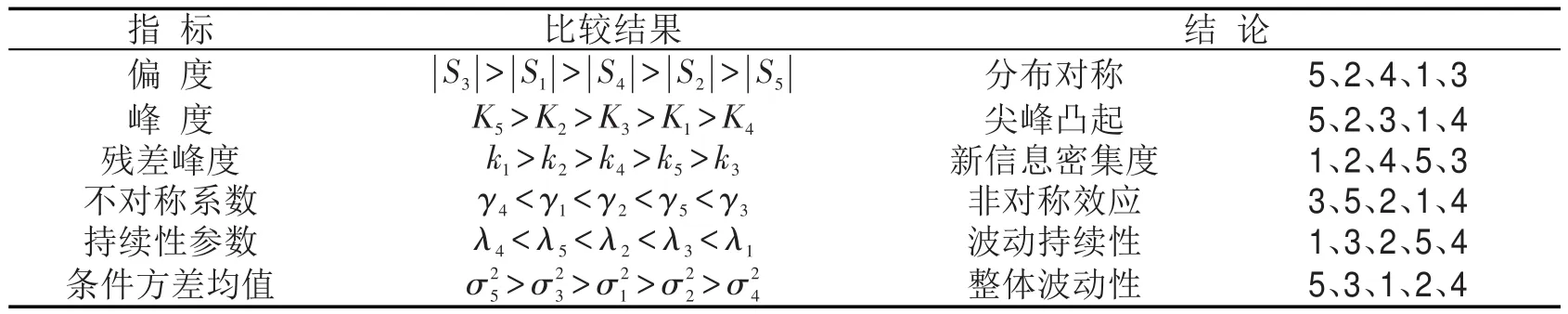
表5 行程时间波动率序列波动特点总结Table 5 Summary of characteristics of travel time volatility
以第3条路径为例,其尖峰凸起程度较高,分布对称性最差,具有明显的尖峰厚尾特征,因此虽然该路径新信息的密集程度不大,但是其波动的持续性较强,吸收新信息的能力较差,尤其是在冲击程度较大的情况.第3条路径对于不同方向上的波动,其吸收能力具有明显的不对称性.
本文所提出的方法是基于计量经济学中的ARCH模型簇对路径行程时间的可靠性进行分析. ARCH模型簇对分析具有集群性、持续性,以及分布厚尾特点的时间序列数据的方差变化特点,具有非常好的效果.ARCH模型簇非常简练地概括了外生变量、滞后的内生变量、时间、参数和前期残差等对于时间序列波动的影响.与交通系统的自身特性也较为吻合,能够有效地刻画路径行程时间波动的时变性与持续性、系统外部信息冲击的分布、系统对外部信息冲击的反应等,从而对路径行程时间的可靠性做出评价.
[1]陈小鸿,冯均佳,杨超.基于浮动车数据的行程时间可靠度特征研究[J].城市交通,2007,5(5):42-45. [CHEN X H,FENG J J,YANG C.Research on travel time reliability characteristics based on floating car data [J].Urban Ttransport of China,2007,5(5):42-45.]
[2]王进,史其信.短时交通流预测模型综述[J].中国公共安全·学术卷,2005,1(1):92-98.[WANG J,SHI Q X. The summary or the short-term traffic flow predicts mod⁃el[J].China Public Security,Academy Volume,2005,1 (1):92-98.]
[3]李玮峰,段征宇,郭高华.基于协整理论的浮动车行程时间修正模型[J].北京理工大学学报,2013,33(1):141-144.[LI W F,DUAN Z Y,GUO G H.Error correc⁃tion model of travel time for floating car data based on co-integration theory[J].Transactions of Beijing Insti⁃tute of Technology,2013,33(1):141-144.]
[4]Engle R F.Autoregressive conditional heteroskedasticity with estimates of the variance of U.K.inflation[J]. Econometrica,1982,50(4):987-1007.
[5]Bollerslev T.Generalized autoregressive conditional het⁃eroskedasticity[J].Journal of Econometrics:1986,31: 307-327.
[6]Glosten L R,Jagannathan R,Runkle D.On the relation between the expected value and the volatility of the nom⁃inal excess return on stocks[J].The Journal of Finance, 1993,48(5):1779-1801.
[7]Nelson D B.Conditional heteroskedasticity in asset re⁃turns:a new approach[J].Econometrica:Journal of the Econometric Society,1991,59(2):347-370.
Route Travel Time Reliability Analysis Based on ARCH Model Cluster
LI Wei-feng,DUAN Zheng-yu,GUO Gao-hua
(Key Laboratory of Road and Traffic Engineering,Ministry of Education,Tongji University,Shanghai 200092,China)
The reliability of travel time is a key index of transportation network reliability.The heteroskedasticity occurs in the variability of travel time because of the uncertainty of traffic network.Thus the travel time cannot be accurately predicted through traditional mathematic statistic method.To cope with the characteristics of clustering,high peak and fat tail,the paper introduces ARCH model cluster in the econometrics. The models are formulated in the empirical analysis to evaluate the volatility and continuity of route travel time variability,describe the distribution of extrinsic information and analyze the response of route travel time variability to the inference of extrinsic information.Results show that ARCH model cluster adapted well to the variability of variance of travel time and corresponded to the features of traffic network.Effective evaluation of route travel time reliability is also obtained.
transportation engineering;reliability;ARCH model cluster;travel time;time series
1009-6744(2014)04-0186-08
U491.2
A
2013-12-20
2014-02-19录用日期:2014-02-24
国家自然科学基金青年科学基金项目(71001079).
李玮峰(1990-),男,上海人,博士生. *
d_zy@163.com
