模拟导弹制导的交通系统路径诱导算法
2014-07-18李苏剑邢恩辉
,李苏剑*,邢恩辉
(1.北京科技大学机械工程学院,北京100083;2.佳木斯大学机械工程学院,黑龙江佳木斯154007)
模拟导弹制导的交通系统路径诱导算法
(1.北京科技大学机械工程学院,北京100083;2.佳木斯大学机械工程学院,黑龙江佳木斯154007)
模拟导弹制导的单车诱导算法利于交通系统优化目标(车流量平衡目标).为避免多车诱导导致的交通拥堵,以模拟导弹制导的单车诱导算法为基础,提出了模拟导弹制导的交通系统路径诱导算法.按照出行需求,对模拟导弹制导的时间最短路径算法进行改进,使算法满足各类单车路径规划目标,以提高单车诱导接受率.系统路径诱导算法以交通系统优化为最终目标,对超出路网通行能力的诱导进行修正,使交通流运行趋势符合驾驶员出行需求.建立系统优化评价指标和系统诱导接受率指标,并以北京部分地区为例进行仿真.仿真结果表明,算法能够达到系统优化目标,同时保证了较高的系统诱导接受率.
交通工程;系统诱导算法;模拟导弹制导;出行需求;系统优化
1 引言
城市交通网络中,车辆导航系统的应用率越来越高.传统的单车诱导算法以单车路径优化为主要目标,分别偏重距离因素[1,2]或时间因素[3-5],忽略单车诱导算法对系统优化的影响.车辆导航系统目前面临的首要难题之一是在同一路网内,多车同时采用只考虑单车路径优化的算法,不利于交通系统最优化,可能造成城市交通的拥挤或堵塞[6].为解决以上问题,以利于系统优化的模拟导弹制导的单车路径诱导算法[7,8]为基础,进行交通系统路径诱导算法研究.
车辆导航系统目前面临的另一难题为交通系统的诱导接受率问题.路径诱导的接受率即提供的路径规划是否满足驾驶员的出行需求(单车路径规划目标).参考文献[9,10]指出,实际交通环境中,驾驶员对时间、距离因素均有要求且较为看重,对路径诱导的选择偏好直接影响了单车诱导接受率.根据交通调查,参考文献[11]将驾驶员的出行需求大体分为:出行时间最短、出行距离最短或出行时间和距离均较短三类.根据参考文献[11]的分类,对参考文献[7]提出的算法进行改进,使之适合各种出行需求的驾驶员.参考文献[12]指出,为协调单车诱导和交通系统诱导,除使单车诱导利于系统优化外,同时应使系统诱导符合单车诱导目标.本文以改进的模拟导弹制导的单车诱导算法为基础,使系统诱导的交通流调整符合单车诱导目标,以提高交通系统诱导接受率.
2 模拟导弹制导的单车诱导算法及改进算法
根据参考文献[7],模拟导弹制导的单车诱导算法协调单车路径规划目标和系统优化目标(车流量平衡目标),避免交通拥堵,使单车路径规划利于系统优化.
2.1 模拟导弹制导的算法原理
根据参考文献[7],导弹理想运行路线是到达目标的特定路线(时间最短的路线、距离最短的路线等).受地心引力等问题影响,导弹不可能按照理想路线运行.实质上,导弹制导提供的路线为协调理想运行和空间状态条件运行的路线.
车辆理想路径规划为满足单车路径规划目标的时间最短路径、距离最短路径等.受交通系统交通流状态影响,车辆按照单车路径规划目标运行可能导致交通拥堵.按照平衡交通流状态等系统优化目标行驶,车辆路径规划可能过度绕远或时间过长.为协调单车路径规划目标和系统优化目标的冲突,采用模拟导弹制导进行车辆路径规划.
2.2 考虑出行需求的单车诱导算法改进
[7]中,单车诱导算法的单车路径规划目标为出行时间最短.为提高单车诱导接受率,根据驾驶员的出行需求对单车诱导算法进行改进.
2.2.1驾驶员出行需求分类
参考文献[11]调查结果表明,驾驶员出行需求主要分为时间最短、距离最短、时间距离均较短三种.
2.2.2 改进单车诱导算法
参考文献[7]提出的模拟导弹制导的时间最短路径算法以单车出行时间最短为目标.针对出行需求分类,对参考文献[7]提出的算法进行改进,使改进算法适用于参考文献[11]指出的三种单车路径规划目标.
改进方法为:求取理想路径和进行动态路径规划的算法不变.实际路径规划协调单车路径规划目标和系统优化目标,需要根据单车路径规划目标进行改进.
参考文献[7]指出,单车路径规划目标为出行时间最短时,理想路径称为时间理想路径.实际路径规划选择标准为:以两条理想路径(系统优化理想路径和时间理想路径)为标准,选择与理想路径所围的面积最小的以车辆所在的路段起点至终点的实际路径.
单车路径规划目标为出行距离最短时,理想路径称为距离理想路径.距离理想路径为路径规划起点与终点的连线.实际路径规划选择标准与单车路径规划目标为出行时间最短时相似,只需将时间理想路径改为距离理想路径.
单车路径规划目标为出行时间、距离均较短时,实际路径规划选择标准改为:以三条理想路径(系统优化理想路径、时间理想路径和距离理想路径)为中心,实际路径规划搜索方法与其他两种相似.
3 提高系统诱导接受率的交通系统路径诱导算法
根据参考文献[7],模拟导弹制导的单车诱导算法利于系统优化即车流量平衡.同一路网内,运用该算法的车辆越多,越利于交通系统优化.当过多车辆同时采用同一路径规划时,可能导致交通拥堵,不能达到系统优化目标.
为保证单车诱导算法的利用率,在模拟导弹制导的单车诱导算法及改进算法的基础上,提出一种交通系统路径诱导算法.针对多车诱导导致的交通拥堵问题,算法以交通系统优化为最终目标,在修正路径诱导过程中,使交通流运行趋势符合驾驶员出行需求.
3.1 算法原理
传统算法分别根据单车路径规划目标和系统路径规划目标确定单车诱导和系统诱导.再将两者进行协调,对单车路径规划进行修正.传统算法的协调(见图1)不一定符合驾驶员出行需求,路径诱导的接受率得不到保证.
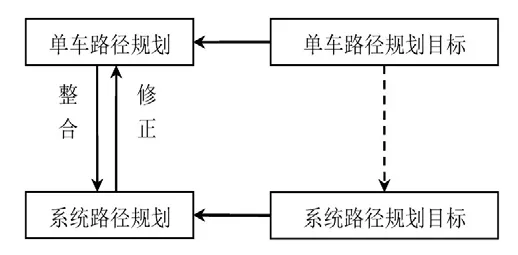
图1 传统方法原理图Fig.1 Schematic diagram of the traditional method
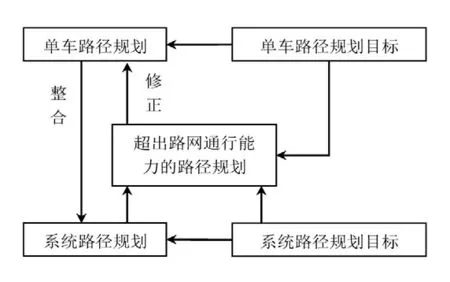
图2 算法原理图Fig.2 Schematic diagram of the proposed method
本文算法在传统算法的基础上,根据交通状况确定超出路网通行能力的诱导.根据系统优化目标及单车诱导目标,对超出路网通行能力的路径规划进行修正.本文算法在路径规划修正时考虑单车路径规划目标,提高诱导接受率.图2为算法原理图.
3.3 路网状态分析
参考文献[12]指出交通系统诱导是将系统所有单车诱导整合,通过物联网平台对于超出交通系统通行能力的车辆重新进行诱导.根据参考文献[12],进行交通系统诱导,首先需要建立未修正前的交通网状态模型.
以路网为基础,对路网状态进行分析.根据实时交通状况,建立实时时间相关网.再根据交通系统诱导目标,建立理想时间相关网.理想时间相关网与实时时间相关网比较得出速度差距网.交通系统诱导将根据速度差距网确定超出路网通行能力的诱导.
3.3.1 实时时间相关网
本文交通系统诱导目标为路网车流量分布均衡,不产生拥堵,各路段及交叉口速度相等.为达到交通系统诱导目标,需表征交通网相对于时间的距离分配,建立实时时间相关网.
实时时间相关网中各路段的值为

式中Vi与路段长度成正比,与总行程时间成反比;li为路段长度;ti为通过路段的时间;t'i为路口等待时间.
3.3.2 理想时间相关网
以路网为基础,建立符合交通系统诱导目标的理想时间相关网.理想时间相关网内,各路段及交叉口车辆均匀分布无拥堵,各路段对应的值V'均相等.
3.3.3 速度差距网
速度差距网中各路段的值为
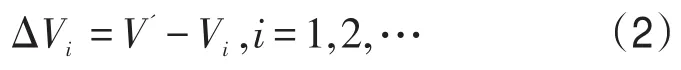
速度差距网表示路网理想交通状态与实际交通状态的差距.通过修正,当速度差距网中的ΔVi值均为零时,交通系统诱导达到目标.
3.4 算法步骤
根据速度差距网,确定拥堵路段相关诱导,即确定超出路网通行能力的诱导.交通系统诱导对超出路网通行能力的诱导进行修正.修正的目标是降低速度差距网的值至零,交通流理想运行趋势按照单车诱导目标趋势.在理想状态下,需要修正的诱导应按照速度差距网满足驾驶员出行需求(最优解)进行修正.为符合系统目标,避免仅满足单一车辆目标导致的拥堵.修正的诱导中超出速度差距网允许范围的诱导选择次优解进行修正.再对二次修正的诱导进行判断,对超出速度差距网允许范围的诱导再次修正.以此类推,至速度差距网的值为零.其中,满足驾驶员出行需求的最优解路径和次优解路径等均由模拟导弹制导的单车诱导算法及改进算法得出.
3.4.1 确定拥堵路段相关诱导
根据速度差距网中各路段的值进行拥堵路段判断.
ΔVi>0时路段为拥堵路段,物联网提供修正触发信号,根据修正触发信号和诱导分布,确定所有包含拥堵路段且未到达该拥堵路段的诱导为拥堵路段相关的诱导.
3.4.2 修正路径诱导
根据ΔVi调整拥堵路段相关诱导车辆,将车辆调整至畅通路段,使所有路段的ΔVi=0,即达到系统优化目标.
由于路网状态实时动态,考虑时间因素,调整时按照车辆即将到达路段的时间先后顺序进行调整,先调整距离ΔVi>0的拥堵路段最近的相关路径.
根据单车诱导目标,未修正前的相关诱导为最优解路径(时间最短路径、距离最短路径或时间距离均较短路径).为满足单车诱导目标,以速度差距网为基础,拥堵路段相关诱导车辆应调整至次优路径.次优路径为修正时除原诱导外符合驾驶员出行需求的最优路径.为避免将车辆均调整至次优路径导致的新拥堵,需要判断调整以后是否会使次优路径超出速度差距网允许范围.如果超出允许范围,部分车辆调整至次优路径,其余路径再通过调整判断调整至第三优路径.以此类推,直至车辆均被调整.
再调整距离ΔVi>0的拥堵路段较远的相关路径,修正方法相同.调整后尽量使速度差距网中相关拥堵路段的值接近零.反复调整,至达到系统优化目标为止.
具体步骤流程图如图3所示.

图3 具体步骤流程图Fig.3 Flowchart of the specific process
4 复杂度及评价指标
4.1 方法复杂度分析
系统路径规划方法复杂度与单车路径诱导方法直接相关.本文采用模拟导弹制导的单车诱导算法.该算法的复杂度与搜索区域内节点数及搜索幅度正相关.驾驶员的出行需求、起讫点分配对系统路径规划算法复杂度影响较大.要降低系统路径规划方法复杂度,除以上因素外,还需考虑系统路径规划中修正路径规划的顺序(时间距离)问题.目前这些问题有待进一步研究.
4.2 方法评价指标
4.2.1 系统优化评价指标
在实际应用中,算法计算速度可能导致算法失效.距离拥堵路段越近的相关诱导对计算速度要求越高.而越近的相关诱导对系统优化的作用越大.为降低算法的计算速度,将算法系统优化目标ΔVi=0改为||ΔVi<δ,δ为常数,单位km/h.
当路网各路段||ΔVi的最大值小于系统优化评价目标时,算法达到预期的系统优化目标.
4.2.2 系统诱导接受率指标
为验证算法,提高系统诱导接受率,需建立各驾驶员n的接受指标:dn,n=1,2,….交通系统诱导提供的诱导满足判断条件时,dn=1;否则,dn=0.
当驾驶员出行需求为出行时间最短时,判断条件为修正的诱导时间小于原诱导.其他驾驶员出行需求的判断条件相似.
5 算例分析
5.1 模型参数
以北京奥林匹克公园附近区域为例对算法进行仿真,路网包含Kehui Road,Kehui South Road, Tatun North Road,Tatun Road路段.路网结构如图4所示.
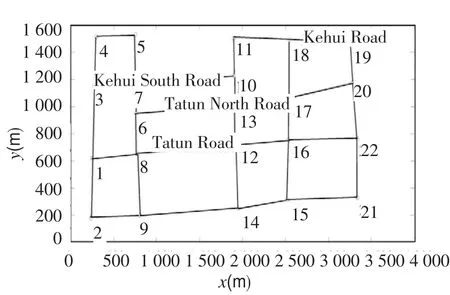
图4 路网图Fig.4 Diagram of the road network
如图4,交通网共22个交叉口,包含起点和终点.各交叉口用圆圈表示,各路段用实线表示.
为保证交通数据的随机动态特性,令各路段及各交叉口初始车辆数随机.采用元胞传输模型方法对交通流状态进行描述.各交叉口的配时方案与实际路网信号配时相同.δ=2 km/h.
假设驾驶员出行需求在驾驶员出行过程中是不变的.根据参考文献[11]对北京地区驾驶员出行需求的调查,选取工作日高峰时段数据作为仿真数据.即驾驶员出行需求中出行时间最短的占61.54%,出行距离最短的占7.93%,出行时间和距离均较短的占29.6%,其它的占0.932%.其中,出行需求为其它的驾驶员占有比例不足1%,为简化模型,假设这类驾驶员出行路线随机.
用matlab软件验证,仿真时间1800 s.
5.2 仿真结果及分析
改变仿真数据,对本文方法5次仿真.
5.2.1 系统优化仿真结果
5次仿真路网各路段||ΔVi的最大值如图5所示.
5次仿真的系统优化评价指标值分别为:0.48、0.77、0.21、0.96和1.34.指标值均小于系统优化评价目标,即||ΔVi<δ,δ=2 km/h.算法达到预期的系统优化目标.
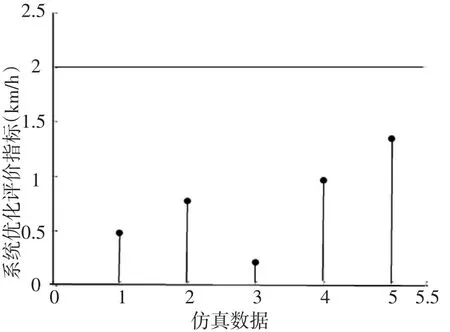
图5 系统优化评价指标Fig.5 System optimization evaluation index
5.2.2 系统诱导接受率仿真结果
参考文献[14]提出的多智能体方法兼顾个体出行者和路网系统管理者在路径选择过程中的利益,协调系统优化目标与单车目标,在一定程度上利于提高诱导的接受率.
将参考文献[14]与本文算法的系统诱导接受率指标仿真结果进行比较,如表1所示.

表1 系统诱导接受率指标值Table.1System guidance acceptance rate index
仿真结果表明:本文算法的系统诱导接受率指标值高于文献[14]的指标值6.11%—26.98%.
6 研究结论
为解决多车诱导导致的交通拥堵问题,提出了模拟导弹制导的交通系统路径诱导算法.算法修正超出路网通行能力的诱导;在对诱导进行修正时,按照单车诱导目标(考虑驾驶员出行需求)进行修正,利于提高交通系统诱导接受率,有益于交通管理;反复修正不超出差距网允许范围,直至差距网达到阈值(符合系统优化目标).本文算法符合实际交通系统发展趋势,提高系统诱导接受率,达到系统优化目标,利于交通系统的智能化和自动化,是车辆交通系统诱导的新方法.
本文假设驾驶员出行需求在出行过程中是不变的,并将驾驶员出行需求作了简单分类.在出行过程中驾驶员出行需求改变及其复杂分类问题,是本文算法有待进一步研究的方向.
参考文献:
[1]Dijkstra E.A note on two problems with graphs[J].Num⁃er Math,1959,1(1):269-271.
[2]Floyd R W.Algorithm 97,shortest path[J].Comm.ACM, 1962,5(6):345.
[3]Vidal T,Crainic T G,Gendreau M,et al.A hybrid genet⁃ic algorithm with adaptive diversity management for a large class of vehicle routing problems with time-win⁃dows[J].Computers&Operations Research,2013,40(1): 475-489.
[4]Tavakkoli-Moghaddam R,Gazanfari M,Alinaghian M, et al.A new mathematical model for a competitive vehi⁃cle routing problem with time windows solved by simu⁃lated annealing[J].Journal of Manufacturing Systems, 2011,30(2):83-92.
[5]Ding Qiu-lei,Hu Xiang-pei,Sun Li-jun,et al.An im⁃proved ant colony optimization and its application to ve⁃hicle routing problem with time windows[J].Neurocom⁃ puting,2012,98(3):101-107.
[6]Ma J,Fukuda D,Schmöcker J D.Faster hyperpath gener⁃ating algorithms for vehicle navigation[J].Transportmet⁃rica A:Transport Science,2013,9(10):1-24..
[7]Gong Yan,Li Su-jian,Xing En-hui.Least-time path al⁃gorithm based on missile guidance[J].Journal of Trans⁃portation System Engineering and Information Technolo⁃gy(English edition),2013,13(6):94-100.
[9]Fonzone A,Schmöcker J D,Ma Jiang-shan,et al.Linkbased route choice considering risk aversion,disappoint⁃ment,and regret[J].Transportation Research Record: Journal of the Transportation Research Board,2012,1 (2322):119-128.
[10]Papinski D,Scott D M.A GIS-based toolkit for route choice analysis[J].Journal of Transport Geography,2011, 19(3):434-442.
[13]马超,崔建勋.基于多智能体的多应急车辆信号优先控制研究[J].交通运输系统工程与信息,2013,13(1): 57-62.[MA C,CUI J X.Multiple emergency vehicles signal priority control based on multi agent approach[J]. Journal of Transportation Systems Engineering and Infor⁃mation Technology,2013,13(1):57-62.]
[14]安实,崔娜,王健,等.基于多智能体协商的路径选择行为仿真研究[J].系统仿真学报,2010,22(8):1890-1894. [AN S,CUI N,WANG J,et al.Multi-agent negotiation approach to simulate and analyze route choice behavior [J].Journal of System Simulation,2010,22(8):1890-1894.]
Traffic System Path Guidance Algorithm Based on Missile Guidance
GONG Yan1,LI Su-jian1,XING En-Hui2
(1.School of Mechanical Engineering,Beijing University of Science and Technology,Beijing 100083,China; 2.School of Mechanical Engineering,Jiamusi University,Jiamusi 154007,Heilongjiang,China)
ract:A simulated missile guidance algorithm is useful for single-vehicle path planning to achieve the system optimization objectives(vehicle flow balance objectives).To avoid traffic congestion caused by a planning algorithm in which multiple vehicles adopt the same path,a simulated missile guidance algorithm for traffic system path planning was proposed based on a simulated missile guidance algorithm for single-vehicle path planning.The least-time path algorithm based on missile guidance was improved in response to drivers’travel demands.The improved algorithm can be applied to all types of single-vehicle path planning objectives and can enhance the guidance acceptance rate.The ultimate goal of the system path guidance algorithm is to optimize the traffic system.To make the traffic flow tendency conform to drivers’travel demands, it modifies the guidance when the road network capacity is exceeded.A system optimization evaluation index and a guidance acceptance rate index were established.An area of Beijing was taken as an example,and the results show that the algorithm can achieve system optimization and ensure a high guidance acceptance rate.
ords:traffic engineering;system guidance algorithm;simulated missile guidance;travel demand;system optimization
1009-6744(2014)04-0180-06
U491
A
2014-03-31录用日期:2014-04-11
国家自然科学基金(50908101).
(1984-),女,吉林通化人,博士生. *
lisujian@me.ustb.edu.com
