基于服务分区的常规公交枢纽布局优化模型

俞洁，潘述亮，刘玥

(1.山东大学控制科学与工程学院,济南250061；

2.威斯康辛大学密尔沃基分校土木工程系，美国威斯康辛州WI 53201)

基于服务分区的常规公交枢纽布局优化模型

俞洁＊1，潘述亮1，刘玥2

(1.山东大学控制科学与工程学院,济南250061；

2.威斯康辛大学密尔沃基分校土木工程系，美国威斯康辛州WI 53201)

为提升公交系统运输效能与服务质量，并针对以往仅从网络流量或土地利用单一角度求解枢纽最优布局问题的局限性，从解析枢纽“服务分区”特性入手，建立“枢纽服务分区、线路干支分离”的城市常规公交枢纽布局优化模型；进而基于网络解构思想简化模型复杂度、探索最优求解算法并加以实现；最后结合苏州工业园区实际案例验证模型与算法普适性，并对模型的关键参数进行灵敏度分析.结果表明：通过引入“服务子区”概念可以从系统最优角度实现交通需求与土地利用互动的数学表述，因而可更科学客观地反映城市公共交通网络服务的实际特性与公交枢纽规划实践.

交通工程；布局优化；整数规划；常规公交枢纽；服务分区

1 引言

近年来，随着城市公交网络的快速拓展、客流换乘强度的增大，我国很多城市的公交系统普遍呈现出公交网络庞杂、重复系数高、换乘不便、服务水平低等尴尬局面.在此情况下，换乘枢纽对公交线网的级配优化作用，以及对网络客流的优化组织作用日渐凸显.然而，目前我国公交换乘枢纽的规划与建设仍显滞后，公交发展过程中存在重线路布设，轻枢纽规划的误区，这也导致公交换乘枢纽往往成为城市客运交通系统的瓶颈，使得高容量公交客运系统的功能与效率无法得到充分发挥.

枢纽布局优化理论方面的研究始于1987年O’Kelly对该问题的数学表述[1，2].归纳看来，城市客运枢纽布局优化理论方面的研究成果可分为四种：

(1)数学解析法[3].适应于在规划范围内只设置一个枢纽的布局问题，如重心法和微分法.

(2)运筹学模型[4-17].适合于多元枢纽布局规划，以运输系统的运输成本最低，或以运输和建设成本组成的总成本最低为目标函数，结合一定的约束条件，确定枢纽布局的最佳方案.近年来，模拟退火算法、神经网络技术、遗传基因算法等启发式算法都被用来改进求解中枢系统枢纽区位布局模型.

(3)交通配流法[18-20].主要是依据网络中交通分配的结果、节点交通流量的大小、或者节点被经过的次数来确定枢纽的布局.

(4)考虑用地性质的客运枢纽分级布局方法[21，22].该方法将城市客运换乘枢纽布局和城市土地利用性质紧密结合，进而提出基于TOD模式的客运换乘枢纽的布局规划方法.

上述客运交通枢纽布局优化方法可以进一步归纳为两类，即“交通流量决定型”与“城市用地布局决定型”.前者是从网络交通流量的角度考虑枢纽布局，但不考虑土地利用性质的影响；而后者则是从城市用地布局结构来对不同等级的枢纽进行位置选择与功能定位，但并未从运输系统最优的角度综合考虑枢纽之间的流量交换关系，同时该方法对城市空间结构依赖性较强，所提出的模型与方法普适性较差.因此，如何从系统最优的角度对上述两类方法进行集成与互补，从而使优化布局模型更科学、客观地反映城市公交网络的实际特性与公交枢纽规划实践，则是本研究需要深入考虑的问题.本研究以常规公交枢纽为对象，并假定研究区域内所有的轨道交通、对外交通枢纽的布局选址方案均是科学合理的，并将这两类枢纽作为常规公交枢纽的衔接换乘对象加以考虑.

2 问题描述

城市公交换乘枢纽布局受到交通需求与城市用地布局的交互影响，脱离其中任何一方面因素考量该问题都将是片面的.鉴于此，本文从土地利用与城市交通需求的有效整合角度出发，提出“枢纽服务分区、线路干支分离”(图1)的城市常规公交换乘枢纽布局优化选址问题.

(1)枢纽服务分区.

从解析枢纽服务范围受需求分布、用地布局、线网级配、枢纽功能等因素影响所呈现出的区域性与交叠性入手，首先将研究区域划分为若干个服务子区，每个子区中只允许设置一个枢纽，同时保证子区内各出行产生/吸引点对枢纽点的可达性，以及各子区枢纽间的连通性.枢纽服务分区的突出优点是可以使后续的公交枢纽布局方法研究避免陷入“流量决定型”方法的局限，使规划者从宏观层面对交通与土地利用的互动协调加以引导.

(2)线路干支分离.

接下来以各子区的枢纽为核心整合公交线网.公交枢纽之间布设面向中长距离出行的大运量公交干线，可采用大站快车等方式为乘客提供快速、准点的服务.子区内部主要布设面向中短距离出行的公交支线，可采用中小型巴士为乘客提高灵活多变的响应式需求服务.应该说，这种“干支分离”的客流组织模式提高了公交网络的覆盖能力和通达性，并使得柔性化、多样化、个性化的“门到门”服务成为可能.

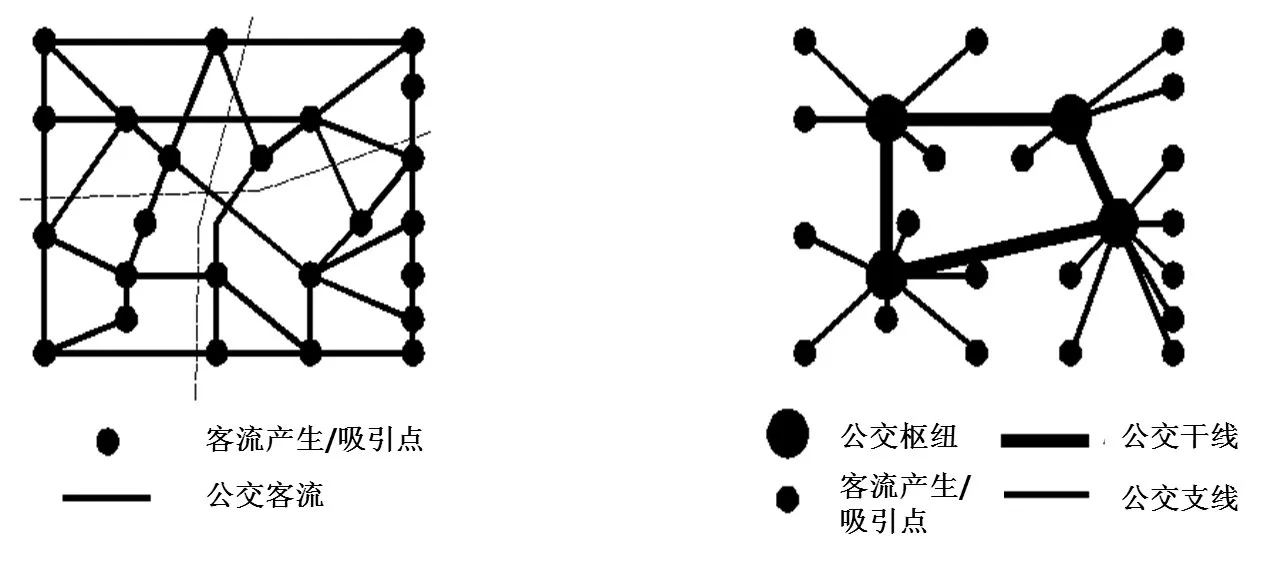
图1 城市常规公交换乘枢纽布局选址问题描述Fig.1 Problem statement for locating urban transit transfer centers

3 模型建立

为了从系统最优角度整合交通需求与用地布局的影响，本文通过设计和引入合理的决策与约束变量，来描述交通需求与土地利用相互影响机理的数学表述，并以核心约束条件的形式将其纳入后续公交枢纽布局优化模型之中，进而真正保证布局优化模型科学、客观地反映城市公共交通网络的实际特性与公交枢纽的规划实践.

3.1 模型假设

为了使研究问题得到简化,本文提出如下假设：

(1)网络中的公交客流由直达客流与换乘客流组成，并假定出行者在一次完整的出行过程中的最大换乘次数不超过2次.乘客根据是否为最短出行时间路径选择直达、换乘一次、或换乘两次.

(2)网络中的公交线路分为两类——干线与支线.枢纽与枢纽之间采用干线相连；枢纽与客流产生/吸引点之间采用支线相连；客流产生点与客流吸引点间如采用直达方式亦采用支线相连.为了体现枢纽之间运输的规模效应，假定干线与支线的平均速度之比为v干线:v支线=1:α(α＜1).

(3)鉴于本研究定位为宏观层面的枢纽布局选址规划问题，因此不考虑道路拥挤对于公交出行时间的动态影响.

3.2 模型参数

模型中涉及的参数及定义如下：

G——研究区域；

N——网络中的客流产生/吸引点的集合；

i——网络中客流产生/吸引点的编号；

(i,j)——客流产生/吸引点i和客流产生/吸引点j之间的路径；

p——网络中需要设置的服务子区数量；

Cr——研究区域内划分的第r个服务子区(r=1,…,p)；

Ci——客流产生/吸引点i所属的服务子区(i=1,…,n)；

wij——从客流产生/吸引点i到客流产生/吸引点j的公交客流量；

α——公交干支线路速度折减系数；

tij——从客流产生/吸引点i直达客流产生/吸引点j的出行时间；

tk——枢纽k的换乘时间；

tijkm——从客流产生/吸引点i到客流产生/吸引点j经由枢纽k、m中转的出行时间, tijkm＝tik+tk+αtkm+tm+tmj，(如换乘一次，m=k,tkm=0,tm=0)；

xij——当从客流产生/吸引点i到j采用直达方式出行时为1，其他情况为0；

yk——当公交枢纽设置在第k个备选点时为1，其他情况为0；

zijkm——当从客流产生/吸引点i到j采用中转方式出行(k=m,换乘一次；k≠m,换乘两次)时为1，采用直达方式时为0.

3.3 模型表述

目标函数

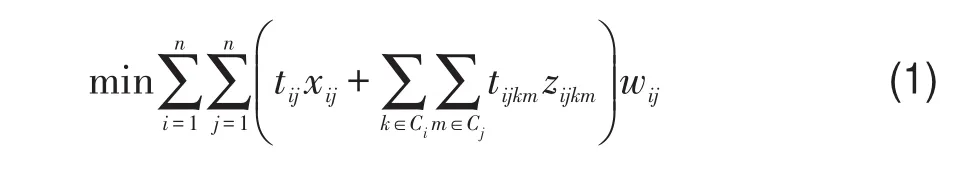
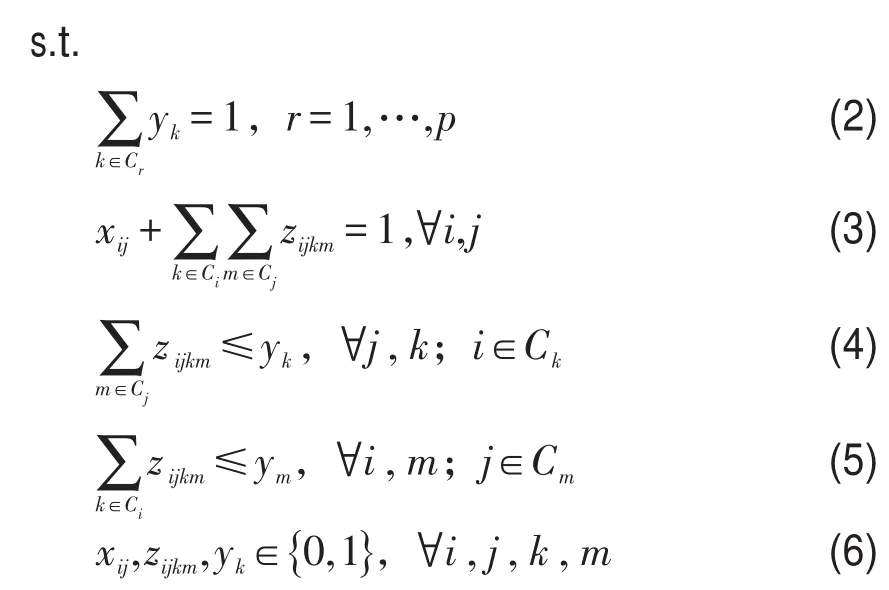
式(1)以研究区域中全体乘客的总出行时间最小化为优化目标；式(2)是每个服务子区只有一个枢纽入选的约束条件；式(3)限定了出行者在从客流产生/吸引点i到客流产生/吸引点j的过程中，仅可选择直接到达、换乘一次(k=m)或换乘两次(k≠m)中的任意一种方式；式(4)、式(5)限定了需要换乘的客流必须经过选中的枢纽k、m；式(6)是决策变量xij、zijkm、yk均为0-1变量的约束条件.

4 模型求解

上述问题为整数非线性规划模型，本文将基于网络解构思想，通过引入辅助决策变量，实现模型的非线性转化以简化模型复杂度，并通过将非线性约束的线性化改进，以确保在合理时间内得到全局最优解.

4.1 模型的非线性转化

如果服务子区的枢纽位置已经确定，可以确定任意服务子区间或服务子区内的公交出行路径，如图2所示.即，如果备选点k、m被确定为枢纽，则从客流产生/吸引点i到客流产生/吸引点j(i,j分别属于k和m所在的服务子区)的出行时间可表示为

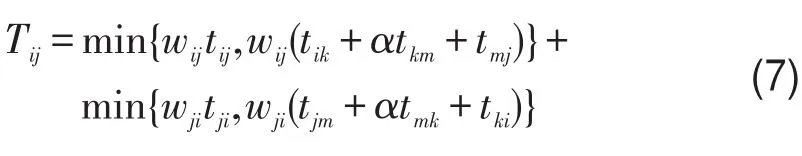
进而，从服务子区Ck到Cm的总出行时间为

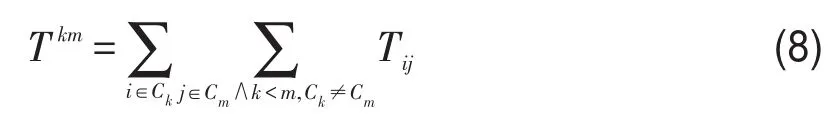
对于特殊情况k=m，Tkm改为Tk.

随后，引入辅助决策变量δkm(k＜m,Ck≠Cm)，当备选点k,m被选为枢纽时为1，否则为0.从而，上述模型可转化为

目标函数(10)对应于式(1)及式(3)；约束条件式(11)对应于式(2)；约束条件式(12)限定了只有在yk与ym同时为1的情况下，δkm才能取1；约束条件式(13)对应于式(6).

4.2 非线性约束的改进

为了解决上述非线性整数规划问题在合理时间内难以获得全局最优解的困难，本文将式(11)进一步转为下述线性约束：

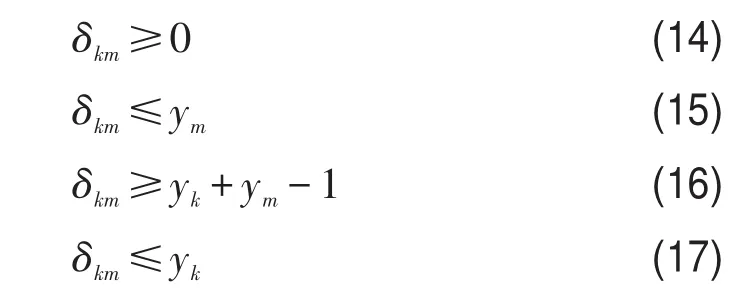
经过非线性约束的改进，该问题再次被转化为线性整数规划模型.与原始模型相比，由于决策变量数的显著缩减，从而可在合理时间内得到模型的全局最优解.

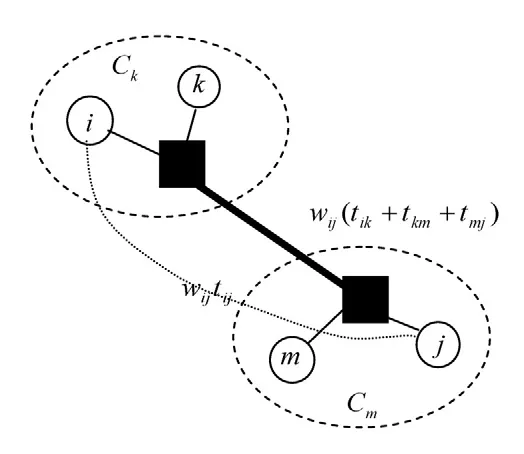
图2 服务子区间最小出行阻抗(时间)路线的选择Fig.2 Minimum demand-weighted total travel time between service zones

5 案例分析

以苏州工业园区(包含58个交通小区)为例，进行常规公交换乘枢纽布局选址规划，如图3所示.

5.1 模型输入与输出

该模型输入的已知条件包括以下4个部分：

(1)公交客流OD分布矩阵及距离矩阵.

(2)依据城市用地规划可将整个园区划分为1个行政区、2个工业区、2个商业区，以及1个大学园区.同时鉴于行政区内存在2个天然屏障（即金鸡湖和新华高速公路），因此，该行政区被划分为3部分，共计8个服务子区，如图4所示.

(3)线路速度：公交支线的平均速度为15 km/h，公交干线的平均速度为30 km/h(即取α=0.5).

(4)假设乘客换乘一次需要的时间为3分钟（根据公交换乘行为调查，以及公交公司实际运营情况调研后取值）.模型输出包括以下3个部分：

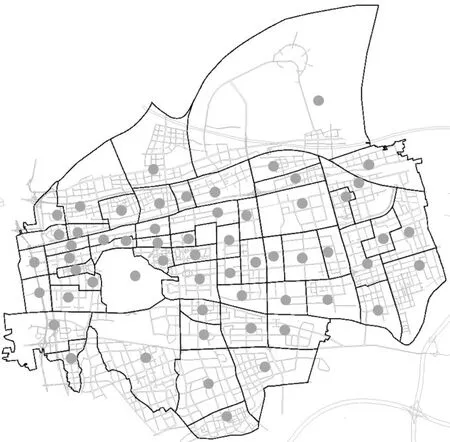
图3 园区交通小区的划分示意图Fig.3 Distribution of TAZs on study network

图4 园区服务小区的划分示意图Fig.4 Clustering rules for study network

(1)系统的运输效率，即研究区域总的出行时间.

(2)枢纽用地地理区位及规模(流入、流出的客流量).

(3)客流产生/吸引点间的路径选择.

使用LINGO 13.0求解公交枢纽布局选址的优化结果(位置及规模)如表1及图5所示.此时，系统中所有乘客的总出行时间为74 050小时，与系统中所有乘客采用直达出行(即不设枢纽)的总时间84 731小时相比，降低了13%.

5.2 参数敏感性分析

为进一步揭示不同服务子区及线路分级对枢纽布局优化结果的影响，本文计算汇总了不同服务子区划分情况(表2)及公交干支线路速度折减系数α所带来的目标函数值的变化情况，如表3及图6所示.可以看出：

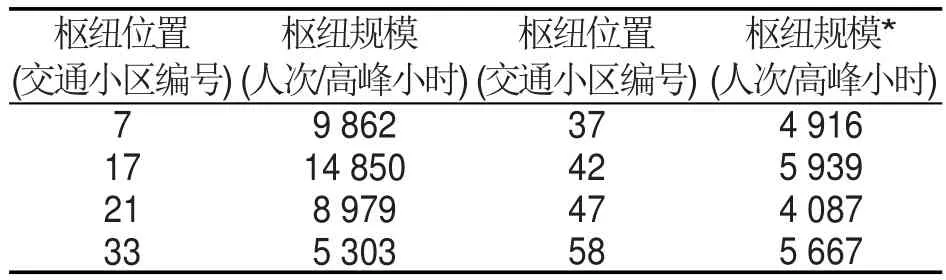
表1 枢纽布局优化位置及规模Table 1 Locations and scales of urban transit transfer centers

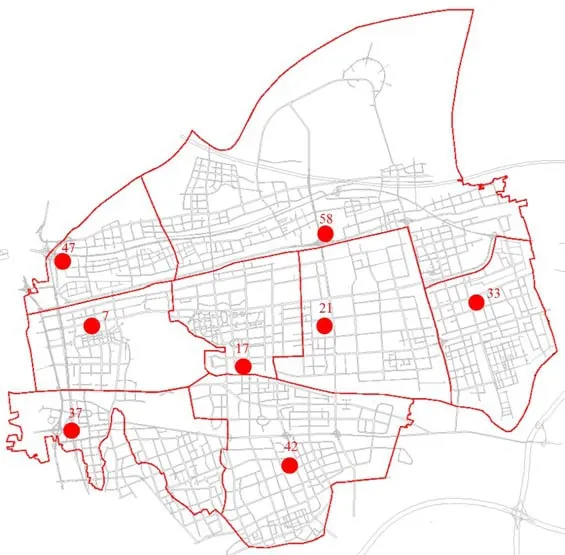
图5 枢纽布局优化位置分布图Fig.5 Optimal locations of urban transit transfer centers

(1)对于给定的α值而言，随着p值的增加，目标函数值会呈现下降趋势.当服务子区数量(也即枢纽数量)较少时，设置枢纽并不能提高公交网络的运行效率.以α=0.5为例，当p≤4时，网络中所有乘客的出行总时间反而大于乘客采用直达出行的总时间；而当p≥5时，随着服务子区设置数量的增加，公交网络的运行效率会得到显著提高.

表2 不同服务子区数量下交通小区服务子区划分情况表Table 2 Clustering rules under different numbers of service zones

表3 不同p值及α值对应的目标函数值(小时)Table 3 Objective function values under different scenarios(hrs)

图6 不同p值及α值对应的目标函数值对比结果Fig.6 Objective function values under different scenarios

(2)对于给定的p值而言，随着α的增加目标函数值有递增趋势.以p=6为例，当0.5≤α≤0.7时，网络中所有乘客的出行总时间小于乘客采用直达出行(即不设枢纽)总时间，而当α≥0.8时，设置枢纽后所有乘客的出行总时间反而大于直达出行总时间.因此，为了提高公交网络的运行效率，需要选择合适的α值，以指导公交线网的优化级配工作.

6 研究结论

本文从城市用地布局与交通需求的有效整合角度出发，以系统运输效率最大化为优化目标，建立了“枢纽服务分区、线路干支分离”的城市常规公交换乘枢纽布局优化模型，并设计了高效求解算法，进而结合实际案例验证了上述模型与算法的有效性.通过引入“服务子区”概念实现了交通需求与土地利用互动的数学表述，在客观上反映了城市公共交通网络服务实际特性与公交枢纽规划实践的同时，可更好发挥公交网络运输的规模经济效应，并进一步指导公交线网优化级配工作.

为了使公交换乘枢纽布局选址模型更能真实反映现实世界的交通情况，后续研究工作需要进一步考虑枢纽的等级特性及网络上实际交通运行状况对乘客路径选择的影响.

[1]O’Kelly M E.A quadratic integer program for the loca⁃tion of interacting hub facilities[J].European Journal of Operational Research,1987,32:393-404.

[2]Deborah L Bryan，Morton E O’Kelly.Hub-and-spoke networks in air transportation:An analytical review[J]. Journal of Regional Science,1999,39(2):275-295.

[3]胡列格,刘中,杨明.交通枢纽与场站[M].北京:人民交通出版社,2003.[HU L G,LIU Z,YANG M.Transport huband the station[M].Beijing:China Communications Press,2003.]

[4]AykinTurgut.Networking policies for hub-and-spoke systems with application to the air transportation system [J].Transportation Science,1995,29:201-221.

[5]Racunica I,Wynter L.Optimal location of intermodal freight hubs[J].Transportation Research Part B:Meth⁃odological,2005,39:453-477.

[6]Campbell J F.Integer programming formulations of dis⁃crete hub location problems[J].European Journal of Op⁃erational Research,1994,72：387-405.

[7]O’Kelly M E.Hub facility location with fixed costs[J]. Papers in Regional Science:The Journal of the Regional Science Association International,1992,71：293-306.

[8]Rodriguez V,M J Alvarez,L Barcos.Hub location under capacity constraints[J].Transportation Research Part E, 2007,43:495-505.

[9]Sung C S,H W Jin.Dual-based approach for a hub net⁃work design problem under non-restrictive policy[J]. European Journal of Operational Research,2001,132: 88-105.

[10]Kim D K,C H Park,T J Kim.Single allocation hub net⁃work design model with consolidated traffic flows.[C]// Transportation Research Record:Journal of the Trans⁃portation Research Board,No.2008,Transportation Re⁃search Board of the National Academies,Washington,D. C.,2007:51-59.

[11]袁虹,陆化普.综合交通枢纽布局规划模型与方法研究[J].公路交通科技,2001,18(3):101-105.[YUAN H,LU H P.Study on model and method of comprehensive transportation terminal planning[J].Journal of Highway and Transportation Research and Development,2001,18 (3):101-105.]

[12]覃矞.轨道交通枢纽规划与设计理论研究[D].上海:同济大学,2002.[TAN X.Study on theory of rail transit ter⁃minal planning and designing[D].Shanghai:Tongji Uni⁃versiry,2002.]

[13]崔叙.城市综合客运枢纽规划与设计理论研究[D].上海:同济大学,2005.[CUI X.Study on theory of compre⁃hensive transit terminal planning and designing[D]. Shanghai:Tongji Universiry,2002.]

[14]李旭宏,肖为周,陈大伟,等.大城市对外客运枢纽布局优化模型[J].交通运输工程学报,2010,10(2):75-81. [LI X H,XIAO W Z,CHEN D W,et al.Layout optimiz⁃ ing model of external passenger transport hub in metrop⁃olis[J].Journal of Traffic and Transportation Engineer⁃ing,2010,10(2):75-81.]

[15]姚锦宝，姚宝珍．基于迭代法优化换乘枢纽布局[J].武汉理工大学学报,2010,34(1):76-79.[YAO J B,YAO B Z.An iteration algorithm for transfer hub optimization [J].Journal of Wuhan University of Technology,2010,34 (1):76-79.]

[16]Yu J,Liu Y,G L Chang.A cluster-based hierarchical model for urban transit hub location planning:Formula⁃tion,solution,and case study[J].Transportation Research Record,the Journal of Transportation Research Board, 2009,2112:8-16.

[17]Yu J,Liu Y,Chang G L,et al.Cluster-based optimiza⁃tion of urban transit hub locations:methodology and case study in China[J].Transportation Research Record, the Journal of Transportation Research Board,2008, 2042:109-116.

[18]刘灿齐.现代交通规划学[M].北京:人民交通出版社, 2001.[LIU C Q.Modern transportation planning[M]. Beijing:China Communications Press,2001.]

[19]王炜,杨新苗,陈学武.城市公共交通系统规划方法与管理技术[M]．北京:科学出版社,2002.[WANG W, YANG X M.CHEN X W.Urban public transportation planning methods and management technologies[M]. Beijing,Science Press,2002.]

[20]魏恒,任福田.人—机参与公交客运枢纽选址方法[J].北京工业大学学报,1991,17(3):36-43.[WEI H,REN F T.Method for site determination of transit transfer cen⁃ters with the aid of computer[J].Journal of Beijing Poly⁃technic University,1991,17(3):36-43.]

[21]吕慎,田锋,李旭宏.组团式大城市客运综合换乘枢纽布局规划方法[J],交通运输工程学报,2007,7(4):98-103.[LU S,TIAN F,LI X H.Layout planning method for urban passenger intermodal transfer points in cluster cities[J].Journal of Traffic and Transportation Engineer⁃ing,2007,7(4):98-103.]

[22]俞洁,杨晓光,尹瑞,等.基于TOD模式的成长型城市公共交通规划研究[J].交通运输工程学报,2007，7(3): 106-110.[YU J,YANG X G,YIN R,et a1.Public trans⁃port planning of developing city based on TOD mode[J]. Journal of Traffic and Transportation Engineering,2007, 7(3):106-110.]

Locating Urban Transit Transfer Centers:A Service Zoning Based Approach

YU Jie1,PAN Shu-liang1,LIU Yue2
(1.School of Control Science and Engineering,Shandong University,Jinan 250061,China；2.Department of Civil Engineering and Mechanics,University of Wisconsin-Milwaukee,Milwaukee 53201,USA)

tract：In response to the need of promoting transport efficiency and service quality for urban transit systems,this paper proposes an optimal location model for urban transit transfer centers by integrating the concepts of“service zoning and route classifying”.It explicitly takes into account that the serving capacity of transit transfer centers will be affected by travel demand distribution,land use,and transit network topology.An efficient reformulation was developed to solve the proposed model and yield the global optimal solution for large-scale real-world applications.The model was successfully applied to optimize the transit transfer center locations in Suzhou Industrial Park,China,with the results of significantly improving the system performance and effectively capturing the interaction between travel demand and land use.

ords：traffic engineering;optimal location;integer programming;urban transit hubs;service zoning

1009-6744（2014）04-0113-07

U491.1+7

A

2013-12-10

2014-05-05录用日期：2014-05-15

国家自然科学基金青年基金项目(51108248);山东省自然科学基金项目(ZR2011GQ002);山东大学自主创新基金项目(2011TB019).

俞洁(1979-)，女，安徽芜湖人，副教授，博士，硕士生导师. *

jie.yu@sdu.edu.cn