信号控制人行横道格子气行人仿真模型

马新露,孙惠芳

（重庆交通大学交通运输学院，重庆400074）

信号控制人行横道格子气行人仿真模型

马新露*,孙惠芳

（重庆交通大学交通运输学院，重庆400074）

以格子气模型为基础，既考虑对向行人的干扰因素，同时考虑了本向行人由于速度差异造成的影响，改进了格子气模型，结合信号控制有倒计时人行横道行人过街特性，提出了新的行人过街格子气仿真模型，并将其编成仿真软件.用该软件对不同快中慢行人比、不同对向行人比、不同规格人行横道的行人过街进行了仿真.结果表明，慢的行人会增加行人总体延误，并且行人到达率越大，速度慢的行人影响越大；行人到达率较小时，对向行人比差距越大延误越小，当行人到达率超过一定值时，对向行人比差距越大延误反而越大；人行横道宽度越宽，行人延误越小，人行横道越长，行人延误增加越明显.在其他因素相同时，改变行人相位时间，在一定范围内随时间的增加，延误降低明显，此后增加行人相位时间对降低延误影响不大.

交通工程；行人流仿真；格子气模型；信号控制；行人过街；行人延误

1 引言

行人仿真模型可分为两类：连续型和离散型.连续型仿真模型中行人的移动空间是连续的，行人依据连续场的作用在空间上移动，主要有气体动力学模型和社会力模型等.气体动力学模型首先由Prigogine and Herman提出，该模型从统计物理学中引入phase-space density(相空间密度)比拟交通中的交通密度.Serge P Hoogendoorn在讨论了交通流离散属性和连续属性的基础上提出了一个通用的气体动力学的交通流模型[1].Dirk Helbing等提出了社会力模型，考虑了行人流的离散特征，社会力模型把行人看作有自驱动力的微粒，每个微粒都拥有一个移动目标并且以一定的速度向目标靠近，速度的大小反映了行人向目标移动时的急切程度[2].2000年又改进了社会力模型，针对逃生恐慌特征的人流进行了模拟[3].离散型仿真模型中行人的移动空间被划分为离散的网格状位置，行人依据一定的移动规则和条件在位置之间移动，按照元胞自动机的更新规则可划分为场域模型、格子气模型等.Ansgar Kirchner提出一种场域模型，该模型建立与行人的移动选择相应位置的静态场域矩阵和动态场域矩阵，场域值越高行人移动概率越大[4].Masakuni Muramatsu等提出了用格子气模型模拟过街行人，该模型中把行人看成气体粒子可以随机移动，对于过街行人有三个方向可以选择，直行和左右移动，当某方向被其他粒子占用，该方向将不被考虑，每个行人根据自己周围的情况有几种移动选择，然后依照各方向概率来选择自己下一步的行动，T Nagatani等针对行人从众行为改进了模型[5，6].

目前，行人的元胞自动机模型多是由物理学者完成的，多用于行人疏散，并且取得了一定成果，但是对人行横道处行人过街的仿真研究很少，并且目前也没有广泛应用的行人过街仿真模拟软件.Vissim仿真软件的行人模拟模块以社会力模型为基础，但是该模块两个方向的行人模拟是通过画两条不干扰的路实现，无法真实地反映对向行人间的相互干扰.格子气行人流模型是一种时间、空间、状态都离散的动力学模型，具有模型简单、容易编程、易于计算等优点.经典的格子气模型在计算机模拟时，采用随机串行更新规则，可以解决行人之间相互冲突的问题，并且在行人运动的过程中可以随时引入随机性，更能真实地描述行人流的运动.本文以格子气模型为基础，考虑对向行人的干扰因素，同时还考虑了本向行人由于速度不同造成的影响，结合行人过街特性提出了新的基于元胞自动机的信号控制人行横道行人过街仿真模型，用C#编程软件将其编成行人仿真软件,并对不同情况下行人过街进行了仿真.

2 行人过街特性

2.1 行人过街心理与行为

对于无信号控制人行横道，行人在穿过人行横道时，要利用车流中出现的安全穿越间隙通过.在信号控制人行横道处，机动车相位时行人在路边等候，当信号灯切换到行人相位时，路边第一排行人开始进入人行横道，后面的行人陆续进入人行横道，行人的速度是不一样的，因此后排速度较快的行人会选择紧跟其后，或者绕过前排速度较慢的行人，当遇到对向行人时，需要停止或者绕过进行避让.信号开始一段时间以后，谨慎过街者选择不进入人行横道，而冒险过街者会进入人行横道并且加快速度，尤其在有信号倒计时的人行横道中，行人会根据相位剩余时间，以及自身情况判断是否进入人行横道，行人相位末期一般不会有新的行人进入，而人行横道中的行人会依照绿灯剩余时间适当地加快脚步通过人行横道.

2.2 行人过街启动时间

过街启动时间是指从人行横道信号灯转为绿灯的时刻，到过街交通实体经过大脑反应意识到可以过街而起步离开路边缘的时刻为止的这段时间.行人过街启动时间受天气、年龄、性别等因素影响.根据调查，夏季男性的平均启动时间是1.47 s，女性是1.65 s，总体是1.56 s；冬季男性的平均启动时间是2.13 s，女性是2.53 s，平均启动时间是2.33 s[7].

2.3 行人过街步速

陈然对上海市行人过街步速进行了调查.上海市行人过街平均速度为1.24m s,平均步幅为0.63m,平均步频为1.96step/s；老年人平均步速1.09m s,平均步幅为0.58m,平均步频为1.87step/s；中年人平均步速1.22m s,平均步幅为0.63m,平均步频为1.95s；青年人平均步速1.30m s,平均步幅为0.65m,平均步频为1.99step/s[8].

3 格子气模型及改进

格子气模型中把行人看成气体粒子可以随机移动，行人过街时有四种可以选择，直行和左右移动，当某方向被其他粒子占用，该方向将不被考虑，假如各方向都被占用则停止.图1是向右行走的行人在移动过程中可能遇到的交通情况及其移动选择，其中×表示被其他粒子(即其他行人)占用.每种交通情形下对应的方向有其对应的移动概率，每个行人个体根据自己周围的情况依照一定的概率来选择自己下一步的行动.

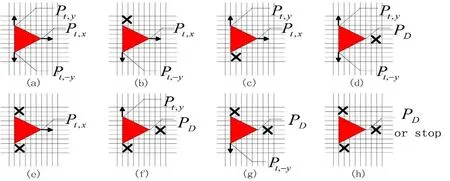
图1 向右行走的行人可能遇到的交通情况及其移动选择Fig.1 Traffic conditions of pedestrians to the right may encounter and his move choice

Masakuni提出的模型只要被其他粒子占用就要考虑改变方向，并且左右方向移动的概率相同，上述几种情况的移动概率如下：

其中，D为飘移强度系数，且0≤D≤1.当D=1时，行人移动的确定性最强；D=0时，行人移动的确定性最弱；随着D的增加，行人移动的确定性增加.Pt,x表示t时刻该行人右行前进的概率.Pt,y表示t时刻该行人上移的概率，相对于行人行走的方向是向左.Pt,-y表示t时刻该行人下移的概率，相对于行人行走的方向是向右.

根据上述模型进行修正，当行人左右方向被其他行人占用或是人行横道边缘时，该方向无法移动，其移动概率为0；但是行人行动前方被占用时，对向行人占用和被本向行人占用的情形是不一样的：

①如果是被对向行人占用要考虑左右“换道”绕过对方，如果周围没有空位就得停止.

②如果是被本向行人占用，就要对比两者的速度，如果前方行人速度快就可以跟在后面，如果前方行人速度相对较慢要考虑是降低自己的速度跟在后面，还是通过“换道”绕过对方.

另外考虑中国行人右行习惯，设定在左右漂移的时候，靠右的概率为0.6，靠左的概率为0.4.

则修正后各情况的移动概率如下：

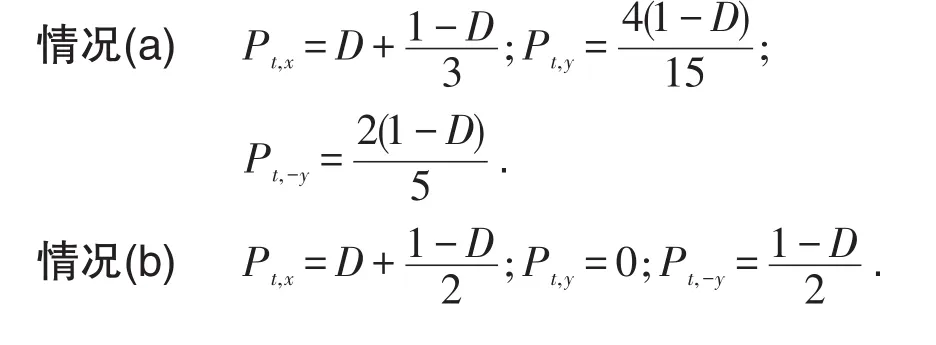
情况(d)

①如果前方被本向行人占用，且V0＜Vfront，则

②如果前方被对向行人占用，且占用位置偏行人左侧，则

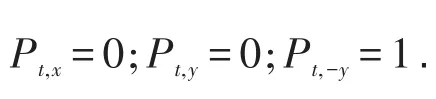
③如果前方被对向行人占用，且占用位置偏行人右侧，则

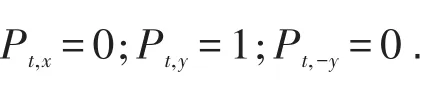
④如果正前方有对向行人占用，则

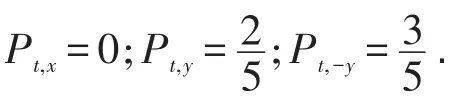
⑤如果前方被本向行人占用，V0＞Vfront，且占用位置偏行人左侧，则

行人以概率PD减速

⑥如果前方被本向行人占用，V0＞Vfront，且占用位置偏行人右侧，则

行人以概率PD减速

⑦如果正前方有本向行人占用，V0＞Vfront，则

行人以概率PD减速

情况(e)Pt,x=1;Pt,y=0;Pt,-y=0.

情况(f)

①如果前方被对向行人占用，Pt,x=0; Pt,y=1;Pt,-y=0.

③如果前方被本向行人占用，且V0＞Vfront，行人以概率PD减速,Pt,x=PD;Pt,y=1-PD;Pt,-y=0.

情况(g)

①如果前方被对向行人占用，Pt,x=0;Pt,y=0; Pt,-y=1.

③如果前方被本向行人占用，且V0＞Vfront，行人以概率PD减速,Pt,x=PD;Pt,y=0;Pt,-y=1-PD.

情况(h)

①如果前方被对向行人占用，行人被迫停止，Pt,x=0;Pt,y=0;Pt,-y=0.

②如果前方被本向行人占用，且V0＜Vfront，Pt,x=1,行人保持原来的速度继续前进.

③如果前方被本向行人占用，且V0＞Vfront，Pt,x=1;Pt,y=0;Pt,-y=0;行人减速.

其中，PD表示行人减速的概率；V0表示该行人t时刻的速度；Vfront表示该行人移动前方的本向行人t时刻的速度.

4 考虑速度差异的信号控制人行横道行人流元胞自动机模型

4.1 模型假设

在不同的过街条件下行人会反映出不同的过街特性，结合我国人行横道信号灯控制实际情况，大多数都有倒计时显示，本文将讨论信号控制且有倒计时的人行横道行人过街仿真模型.根据信号控制且有倒计时的人行横道行人过街特性，对模型做如下假设：

（1）行人到达随机，服从泊松分布.

（2）行人都是遵守信号灯的，并且只前进或停止，不能向后退.

（3）行人进入人行横道时，会判断能否过街，当行人过街相位剩余时间小于过街时间加上启动时间，行人将选择不进入人行横道.启动时间取1.5s.过街时间要考虑行人密度因素，在HCM2010中行人速度与密度呈线性关系，将单位ft换成m、min换成s后，斜率大约为-0.31,因此v1=-0.31K+v0(v1为考虑密度影响后的理论速度，m s；v0为行人期望速度，m s；K为行人密度，即人行道上单位面积的行人数，pm2)，判断过街时间大约为L v1，L为人行横道长度.

（4）在仿真的时候假定每种人在正常情况下都以自己对应的速度行走(期望速度)，假如遇到障碍减速或停止后，一旦前方有空间又立即恢复自己对应的速度.

根据国内外步速研究，这里将过街行人按速度快慢分为三种：①速度较慢的人群多为老年人，其对应步速为1.0m s；②正常速度的年轻人，其对应步速为1.2m s；③速度较快的人，其对应步行速度1.4m s.

（5）考虑到各种行人步速步幅不一样，这里将元胞单元格设为10cm×10cm，由于行人静止时所需空间为0.3m2[9]，则静止行人占用6×5个元胞，速度慢的行人在运动过程中每次占用6×10个元胞，同理正常速度行人运动占用6×11个元胞，速度快的行人占用6×12个元胞.

（6）一个元胞格只能被一个行人占用，但是一个行人可以同时占用多个元胞格.

（7）根据调查，老年人步频在1.87step/s左右，青年人在2step/s左右，仿真模型取行人步频都是2step/s，系统更新时间以行人一步为单位时间，即0.5s.

4.2 仿真流程图

仿真模型采用同步更新规则，系统开始检测是否为行人相位绿灯，在行人绿灯时，先检测每个行人周围交通情况，根据格子气模型的行走概率进行更新，行人仿真流程图如图2所示.根据绿闪时间内行人会加快脚步，软件内设置绿闪末尾清空人行横道，同时将剩余时间和先前行走时间一起记录到实际行走时间当中，表示绿闪期间少部分未走完的行人加快脚步到达人行横道对面.模型输出数据为行人延误，行人延误=行人实际过街时间-行人理论过街时间，行人实际过街时间=路边等候时间+人行横道通行时间（在仿真软件里表现为出现到消失的时间），行人理论过街时间是行人以期望速度通过人行横道所需时间，即行人理论过街时间=L/行人速度.

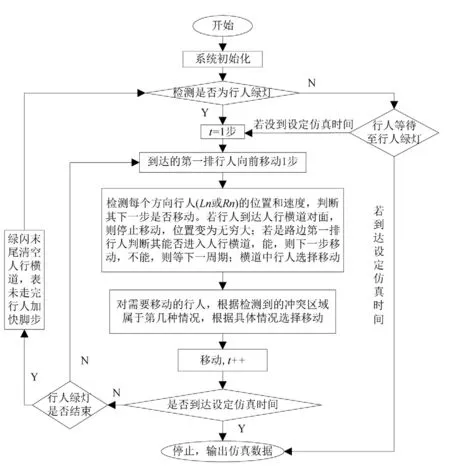
图2 行人仿真软件流程图Fig.2 Pedestrian simulation software flow chart

4.3 仿真结果

根据上述行人流模型编成基于元胞自动机的信号控制人行横道行人仿真软件，分别对快中慢行人比不同、对向行人比不同以及不同规格的人行横道几种情况进行了仿真.

4.3.1 不同快中慢行人比行人仿真

在仿真软件中设定人行横道长度为10m，宽度为4m，信号周期为60s，行人绿灯时间为20s，绿闪时间为5s，漂移强度系数和减速概率均为0.5，并分别对到达率为0.04ped/(m·s)、0.14 ped/(m·s)、0.42ped/(m·s)、0.69ped/(m·s)时，快中慢行人比分别为1:2:7、1:4:5、1:6:3、3:4:3、1:8:1、3: 6:1、5:4:1、7:2:1的情况进行了模拟，得出延误对比如图3所示.当Q=0.04ped/(m·s)和Q=0.14 ped/(m·s)时，延误曲线几乎重合，说明当到达率低于一定值时，行人的到达率的大小对行人的延误影响不大，同时快中慢行人比对延误的影响也不大，此时行人的延误主要和信号灯及人行横道的一些物理属性有关；当Q=0.42ped/(m·s)时，行人延误稍有增加，但快中慢行人比对延误的影响不大；当Q=0.69ped/(m·s)时，行人延误明显增加，并且当较慢的行人占绝大多数时，行人延误显著增加.同时四条曲线都呈下降趋势，表明慢的行人会增加行人总体延误，行人到达率越大，速度慢的行人对延误的影响越大.

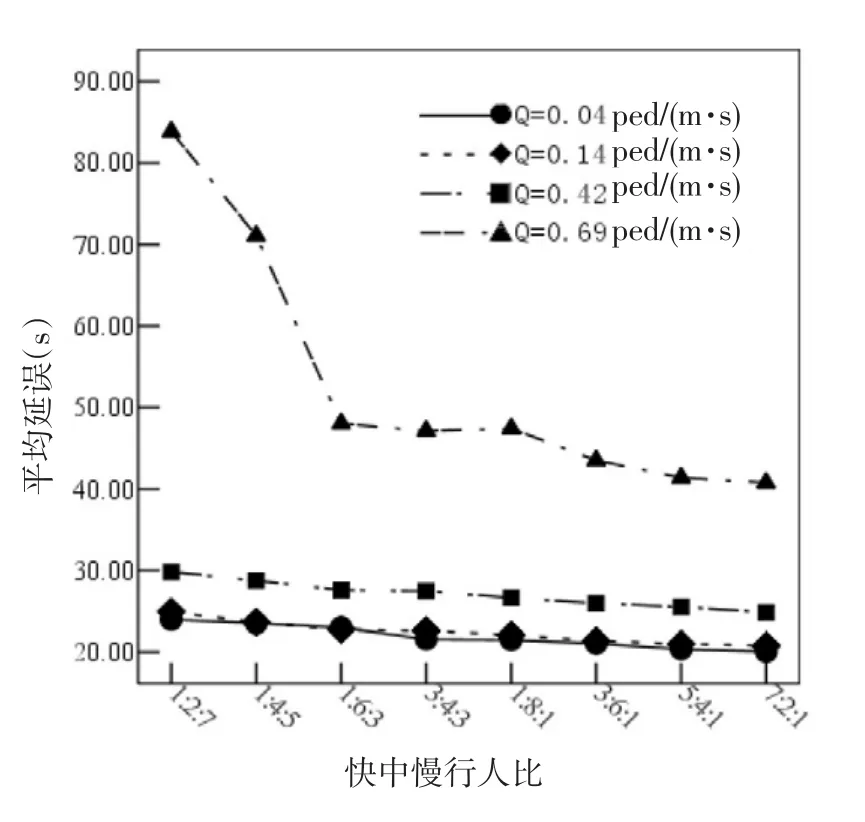
图3 不同到达率下不同快中慢行人比平均延误对比Fig.3 Under different arrival rate average delay comparison at different speed pedestrian ratio

4.3.2 不同对向行人比行人仿真

同样在人行横道长度为10m，宽度为4m，信号周期为60s，行人绿灯时间为20s，绿闪时间为5s，漂移强度系数和减速概率均为0.5的情况下，分别对到达率为0.04ped/(m·s)、0.14ped/(m·s)、0.28ped/(m·s)、0.42ped/(m·s)时，对向行人比分别为1:9、2:8、3:7、4:6、5:5的情况进行了模拟，得出延误对比如图4所示.行人到达率较小时，对向行人比差距越大延误越小，当行人到达率为0.14 ped/(m·s)，对向行人比差距对延误影响不大，随着行人到达率的增加，对向行人比差距越大反而增加延误.因为行人过街延误既受本向行人影响，也受对向行人影响，当行人量低于一定值时，主要受对向行人影响，对向行人比差距越大受对向行人影响越小；当行人量达到一定值时，如果一方行人特别多，后面的行人受前方行人影响较大，因而对向行人比差距越大延误越大.

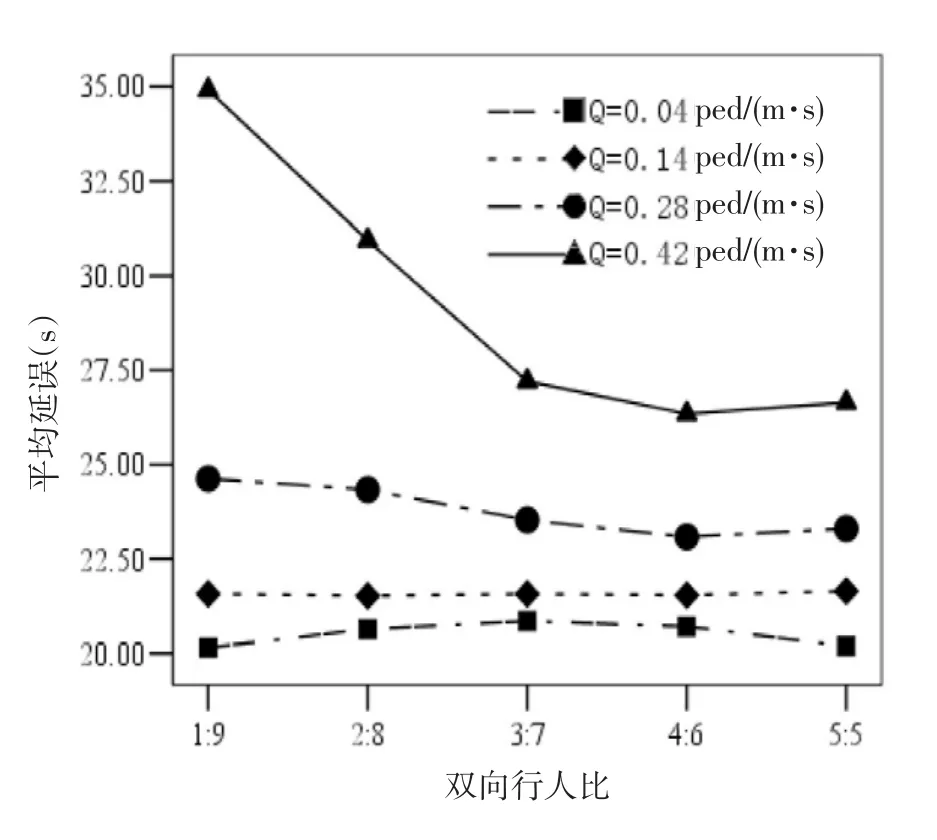
图4 不同到达率下不同对向行人比平均延误对比Fig.4 Under different arrival rate average delay comparison when pedestrian phase time is different

4.3.3 不同规格人行横道行人仿真

在信号灯周期不变，行人到达率都为2 000 ped/h的情况下，对长宽分别为10m×4m、10m× 6m、14m×4m、14m×6m四种规格的人行横道，分别观察其行人相位为20s、25s、30s、35s、40s的行人流模拟，得出延误对比如图5所示.人行横道宽度越宽，行人延误越小，并且在行人相位越小时越明显；人行横道越长，行人延误增加明显.在其他因素相同时，改变行人相位时间，在一定范围内随时间的增加，延误降低明显，此后增加行人相位时间对降低延误影响不大.

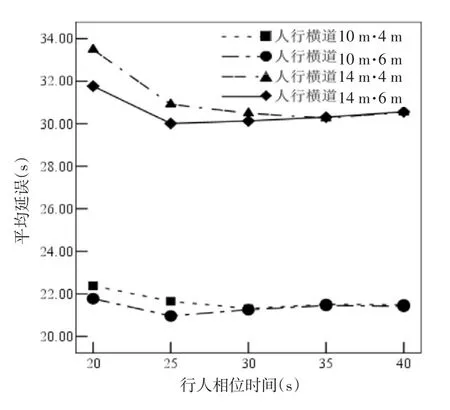
图5 不同规格人行横道行人相位时间不同时平均延误对比Fig.5 Under different specifications crosswalks average delay comparison at different bi-direction pedestrian ratio

5 研究结论

本文以人行横道为研究的交通环境，以双向行人为研究的交通实体，在考虑行人步行速度差异的前提下，基于Masakuni Muramatsu等提出的格子气行人流模型构建了信号控制下的行人通过人行横道的仿真模型.在仿真模型中，信号中后期，行人会衡量能否过街，在可能通过的时间内会选择过街，速度较慢的行人会稍显谨慎，这符合行人过街特性；同时模型中设置绿闪时间行人会加快脚步，也是行人过街的一种现象；并且模型考虑了中国行人靠右行的习惯，更符合现实情况.利用该模型对人行横道物理特性、行人步速快中慢的分布情况、信号灯配时状态对行人通过人行横道时产生的延误影响进行了仿真.

[1]Serge P Hoogendoorn,Piet H L Bovy.Generic gas-kinet⁃ic traffic systems modeling with applications to vehicu⁃lar traffic flow[J].Transportation Research Part B,2001, 35:317-336.

[2]D Helbing,P Molnar.Social force model for pedestrian dynamic[J].Physical Review E,1995,51(5):4282-4286.

[3]D Helbing,I Farkas,T Viesek.Simulating dynam

ical features of escape panic[J].Nature,2000,407:487-490.

[4]A Kirchner,A Schadschneider.Simulation of evacuation processes using a bionics-inspired cellular automaton model for pedestrian dynamics[J].Physical A,2002, 312:260-276.

[5]M Muramatsu,T Irie,T Nagatani.Jamming transition in pedestrian counter flow[J].Physical A,1999,267:487-498.

[6]Tajima,Yusuke,Kouhei Takimoto,et al.Pattern forma⁃tion and jamming transition in pedestrian counter flow [J].Physica A:Statistical Mechanics and its Applica⁃tions 313.3(2002):709-723.

[7]路婷.路段人行横道信号设置影响因素分析及控制方法研究[D].长春：吉林大学,2011.[LU T.Research on factors analysis and control methods of the midblock crosswalks signal setting[D].Changchun:Jilin University,2011.]

[8]陈然,董力耘.中国大都市行人交通特征的实测和初步分析[J].上海大学学报(自然科学版),2005,11(1):93-97.[CHEN R,DONG L Y.Observations and prelimi⁃nary analysis of characteristics of pedestrian traffic in Chinese metropolis[J].Journal of Shanghai University (natural science),2005,11(1):93-97.]

[9]顾金刚.路段行人过街信号设置方法及实例研究[D].长春：吉林大学,2010.[GU J G.Method and case study on signal setting of pedestrian crossing in road sections [D].Changchun:Jilin University,2010.]

Lattice Gas Simulation Model of Pedestrian at Signalised Crosswalks

MAXin-lu,SUN Hui-fang
(School of Transportation,Chongqing Jiaotong University,Chongqing 400074,China)

ract:Based on the lattice gas model,this paper improved the lattice gas model considering both the interference factors of opposing pedestrians and the impact of synclastic pedestrian due to different speed.It proposed a lattice gas simulation model of pedestrian crossing and compiled simulation software,combining with pedestrian crossing characteristics at countdown signalised crosswalk.The study carried out the pedestrian crossing simulation at different speed pedestrian ratio,different bi-direction pedestrian ratio and different specifications crosswalks by the simulation software.The results indicate that slow pedestrians will increase the overall delay of pedestrians and the pedestrian arrival rate higher,the slow pedestrian impact greater. When pedestrian arrival rate is low,the greater the gap between bi-direction pedestrian,the smaller the delay is.When the pedestrian arrival rate exceeds a certain value,the greater the gap between bi-direction pedestrian,the greater the delay is.The wider the crosswalk,the smaller pedestrian delay is.And the longer the crosswalk,pedestrian delay increased significantly.When other factors are the same,changing the pedestrian phase,delay reduced significantly with the increase of time in a certain range.And over this range increasing pedestrian phase time has little effect on delay.

rds:traffic engineering;pedestrian flow simulation;lattice gas model;signal control;pedestrian crossing;pedestrian delay

1009-6744（2014）04-0059-07

U491.2

A

2013-12-26

2014-03-23录用日期：2014-04-03

重庆交通大学教育创新基金项目资助(20130107).

马新露（1981-），男，重庆万州人，副教授，博士. *

maxinlu2002@163.com