快速公交系统离散仿真框架的设计和实施

Fergyanto E.GUNAWAN

（建国大学，雅加达11480，印度尼西亚）

快速公交系统离散仿真框架的设计和实施

Fergyanto E.GUNAWAN*

（建国大学，雅加达11480，印度尼西亚）

世界范围内，快速公交系统是缓解许多城市交通拥挤问题的有效方法之一.然而，系统的成功与否依赖多种因素，如服务规划、基础设施、车站设计、乘客信息系统及系统的集成和接口等.本文基于离散事件系统，构建了快速公交系统（BRT）的计算机仿真框架.这种方法在评估各种变量对BRT运行效果的影响时能够节约成本.结果表明，一部分子系统能够直接用于模拟典型的BRT系统.数值试验证明，开发的子系统能够合理地再现实际BRT系统中的常见情况.

城市交通；离散事件仿真；数值模型；交通拥挤；快速公交系统

1 引言

许多既有研究成果证明了这一工作的必要性和重要性.Campo[2]为世界范围内的城市公共交通提出了基于BRT系统的快速调度方法，如图1所示，基于BRT的公共交通系统数量快速增长.1974年该系统在巴西的库里蒂巴首先建立[3]，最初的支持率并不高.然而，在过去十年里，应用BRT系统的城市快速增加，并且出现了大规模的BRT系统，比如建于2000年12月的TransMilenio系统，建于2004年1月的TransJakarta BRT系统，以及建于2010年2月的广州BRT系统[4].

图1 基于BRT和基于轨道的公共交通系统的运营数量[2]Fig.1 The number of BRT-based systems and rail-based systems in operation[2]

由此可见，为BRT系统开发的计算机仿真模型有很大的应用潜力，比如研究系统的服务水平，评价某些措施的效果，甚至研究BRT系统对环境的影响等，例如，Nugroho等[5]将结构方程模型扩展至空间维度来进一步解释BRT交通走廊中二次污染的传播问题.

学者们很早就意识到了交通系统的计算机仿真模型的重要性，并且从诸多问题中得到了丰硕的研究成果[6-13].Valiguran等[13]构建了一种基于轨道的交通系统.Visser等[9]提出了基于离散事件仿真的智能交通系统的评价框架.Dos Santos Silva等[12]利用离散事件仿真和多准则决策分析法（Multi-criteria DecisionAnalysis,MCDA）优化了钢铁制造公司的闭环海运船队规模.Alves等[8]利用离散事件仿真和虚拟现实技术模拟了物流系统的运行过程.Li等[7]应用离散事件仿真研究了中国城市交通中公共汽车通行效率的影响因素.

2 模型构建

2.1 BRT系统的标准模型

为开发BRT子系统，首先将一般BRT系统简化到至少包含真实BRT系统所有必要的子系统.这种最简化的模型，称之为标准模型，如图2所示.

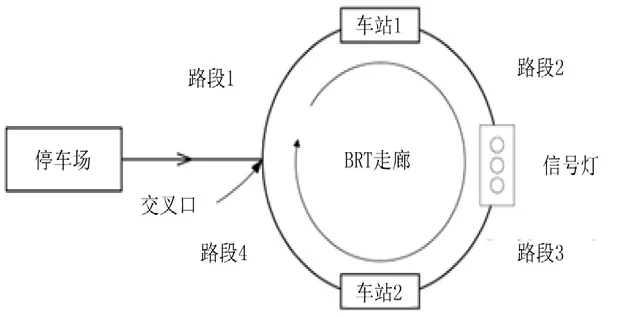
图2 BRT运输走廊的标准模型Fig.2 A canonical model of a BRT corridor

图2是BRT运输走廊的最简形式，走廊中的每辆车按照时刻表从停车场发车.时刻表应该与车辆的发车频率高度相关，尤其在高峰小时，如表1所示.然后，车辆通过路段1到达车站1.在TransJakarta BRT系统中，路段长度在0.3 km至1 km之间[14].车辆在车站1上下乘客后开往车站2.最后这辆车在走廊中循环行驶直至时刻表的终点，现代BRT系统要求运营至晚间[1].在实际BRT系统中，车辆服务很多车站，例如TransJakarta BRT系统中每个走廊有15-26个车站[14].

表1 高峰时段现代公共汽车的频率要求[1]Table 1 Modern requirement for bus frequency during peak period[1]

很明显，图2中标准模型需要必要的子系统来建立BRT系统走廊.这些子系统包括车站、路段、车辆停车场、交叉口、信号灯等.在下文中，将会讨论利用Matlab仿真事件模块进行每个BRT子系统的开发.

2.2 车站子系统

BRT系统的车站非常关键，很多交通活动在这里发生.为了乘客上下车，车辆必须在车站停靠，并且为了提高乘客上下车效率，车站站台应与车辆的地板同高度，使得上下车能在很短时间内完成.与常规公共交通系统相比，BRT车辆明显更加高效，这得益于BRT系统的三个重要设计：车站站台与车辆地板同高、车辆外收费及较宽的车门[1].

BRT车站的一个重要特点是系统能够准确地获得乘客到达车站的动态情况.这方面的重要研究成果包括O’Flaherty和Mangan[15]、Salek和Machemehl[16]、Fan和Machemehl[17]、Luethi等[18]、Islam和Vandebona[19]及Gunawan等[20]，其中一些研究成果利用数学解析方法描述了这种动态情况.

已有研究提出了乘客的系统动力学方法并有如下结论.概括来说，乘客的到达时间服从两种概率分布函数.根据车辆的车头时距分为均匀分布和对数正态分布，如图3所示.

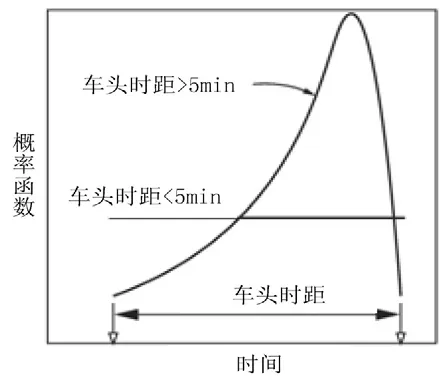
图3 不同公共汽车车头时距下乘客到达的概率函数Fig.3 Probability of passenger arrivals as a function of the bus headway

车辆的车头时距较短时，比如少于5 min，乘客的到达时间倾向于服从均匀分布，意味着乘客的到达是随机的；车辆的车头时距较长时，比如大于5 min，乘客的到达时间倾向于服从对数正态分布.在后面的案例中，多数乘客会按照车辆时刻表的前几分钟到达，前4 min左右的居多.多数研究将5 min的车头时距定义为车辆到达模型的临界值，需要说明的是，Fan和Machemehl[17]将两种分布的临界值取为10 min.

部分文献提出乘客的等待时间（w）是车头时距（h）的函数，车头时距较短时w=h/2[17].该模型建立在三个假设之上：①乘客的到达是随机的；②车辆到达是有规律的；③每位乘客都能坐上他们到站后的第一辆车.事实上，BRT车辆的车头时距变化可能很大[21].为了将此考虑在内，Osuna和Newell[22]、Holroyd和Scraggs[23]及Welding[24]建议按照以下公式计算：

式中w¯是乘客等待时间的期望；μ是车头时距的平均值；s2是车头时距的方差.此外，还有多种经验公式，比如参考文献[15]、[25]和[16]中的公式分别为

为了描述这些特征，车站子系统的设计如图4所示.子模块包括两部分：下层子模块和上层子模块.下层子模块的实体表示一位乘客，上层子模块的实体表示一辆车.

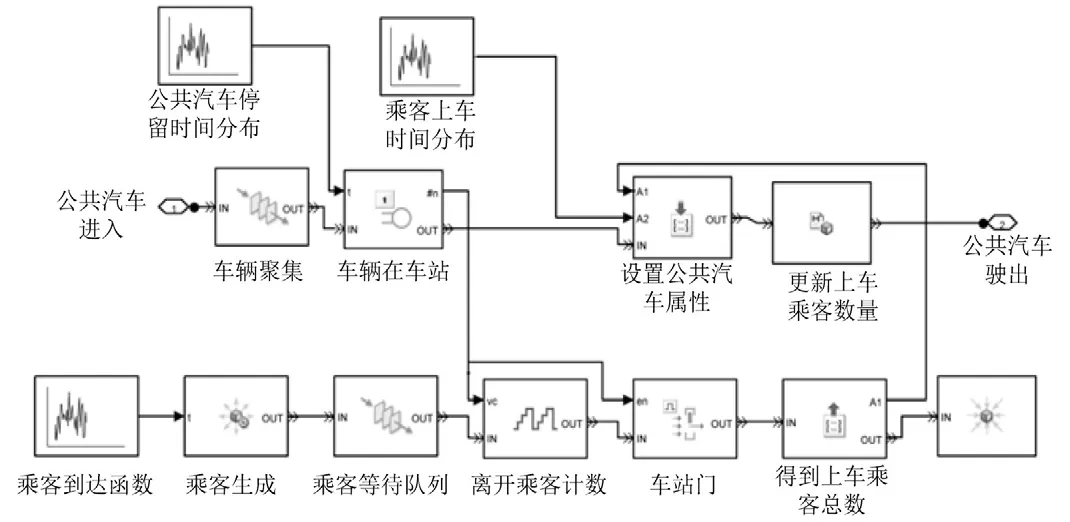
图4 BRT车站的仿真事件模块组成Fig.4 SimEvents block components for the BRT bus station

下层子模块始于乘客到达函数，本质上是一种反映乘客到达特性的统计函数.这个模块给乘客生成模块传递信号使其创建乘客到达事件，生成的乘客被传送到“先到先服务”队列中，乘客在队列中等待直到车门打开.当车辆到达并停靠在站台时，上层子模块就会发出信号打开车门.

上层子模块始于车辆进出车站的停靠区域.上层子模块的设计允许车辆聚集，车辆聚集是现代BRT系统面临的最大问题.当车站为空，车辆停靠在车站，停靠时间由车辆停靠时间模块根据停靠时间分布函数确定.随后，车辆实体会获得下车人数和在队列中等待需要上车的人数的数据.最后，车辆更新数据，保存为车辆属性数据和从该车站离开到下一车站的数据.

2.3 路段子系统

路段子系统必须能够仿真BRT车辆在走廊中的路段上的行驶过程，路段由两个临近车站连接.子系统的特征包括车辆行驶时间和路段上的车辆数量，并包含一个简单的“先到先服务”规则的排队模型.这种方法合理考虑了大多数专用道是1个车道的情况，因此无法超车.

研究和观测结果表明，车辆的行驶时间是服从单参数的指数分布，参数的大小受车辆平均行驶速度或平均行驶时间的影响（例如，Gunawan[21]等）.

图5是Matlab执行仿真事件的设计.设计允许车辆在路段上聚集，车辆行驶时间由该模块决定，该模块详细地给出了车辆行驶时间的统计分布.

图5 路段子系统的仿真模块组成Fig.5 SimEvents block components for the road-segment sub-system

2.4 停车场子系统

停车场子系统能够按照时刻表生成BRT车辆，其中，每个实体表示一辆车.仿真事件的执行过程如图6所示.子系统开始于车辆离开模块的时刻表，在车辆离开模块中，车辆的时刻表是确定.当车辆到站，车辆离开模块就会在每单位时间释放一辆车.因此，不允许停车场子系统在单位时间的服务对象多于一辆车.接着，子系统将记录车辆的离开时间，再分配一辆车.最后，给每辆车创建或附加一些包含乘客数据的属性：车上的乘客数和上一车站乘客上下车数.

图6 停车场子系统的仿真模块组成Fig.6 SimEvents block components for the pool of buses sub-system

2.5 交通信号子系统

交通信号子系统必须能够仿真BRT车辆通过手动控制的交通信号的行驶过程.因此，系统特征为信号灯的周期时长tc和绿灯时长tg，并且该子系统允许车辆在信号灯处排队.

为了达到上述目的，交通信号子系统的设计如图7所示.子系统主要利用“先到先服务”排队规则来指导车辆在信号灯前的等待，“先到先服务”模块之后是交通信号配时模块.“先到先服务”模块本质上是一个释放接口，接口会根据交通信号配时模块的时间打开.当接口打开之后，车辆可以前进.配时模块是两个变量的时间函数：交通信号周期时长tc和绿灯时长tg.

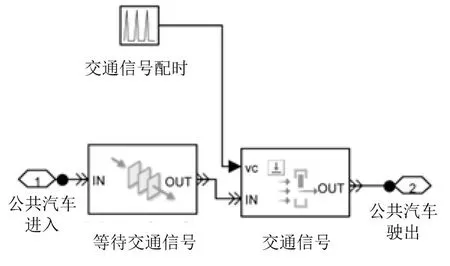
图7 交通信号子系统的仿真事件模块组成Fig.7 SimEvents block components for the traffic signal sub-system

图8证明了这一子模块的应用.在案例中，共有30辆车从停车场中被派出，信号灯周期时长设置为20 s，绿灯时长为5 s.从图中可以看出，在绿灯时，子系统允许车辆行驶，绿灯外的时间全部被禁行.

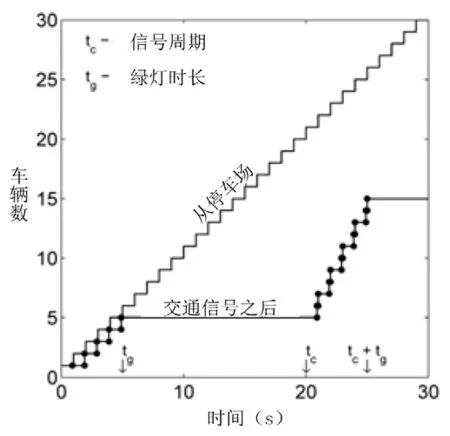
图8 交通信号子系统的测试案例Fig.8 A test case of the traffic signal sub-system

3 数值试验

3.1 乘客到达模型

本节将进行数值试验用以证明乘客到达BRT车站与车辆到达之间的关系，并讨论试验结果.这种关系相对简单，车头时距越长，排队乘客数的期望越大.此外，从目前的计算机仿真模型中获得的乘客排队时间，在一定程度上与通过现有乘客排队模型的预测结果一致，见式（1）和式（4）.

在讨论之前，需要重新说明BRT车站模型.车站子模型本质上包括两个子模块：上层子模块和下层子模块.上层子模块包含排队服务部分，允许车辆在车站聚集等待.下层子模块建立了乘客到达模型.下层子模块的实体是乘客，乘客排队直到上层子模块中的车辆到达.一旦车辆停靠，下层子模块就会开放接口释放乘客，计算上车人数，并将这一数据传输给上层子模块，接收到的乘客人数将会被保存在上层子模块的车辆属性数据中.

为了评价BRT车站模型，建立如下输入数据的数值试验.乘客随机到达车站，以每分钟2位乘客的平均到达概率服从指数分布.这一结论是早期由Gunawan等[20]得到的，作为许多TransJakarta BRT车站的准则.车辆在通过一个路段之后按照指数分布随机到达车站.车辆的车头时距平均值为5 min.这一假设依据Gunawan等[21]的观测，他们得到TransJakarta BRT车辆的行驶时间，如图9所示.

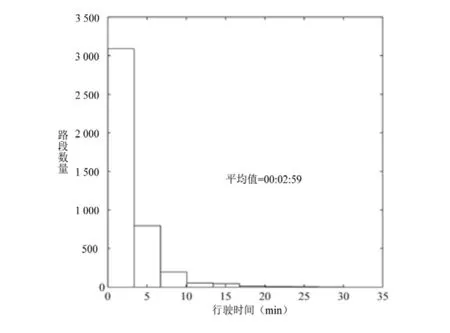
图9 TransJakarta BRT中车辆在两个临近车站的行驶时间分布[21]Fig.9 Distribution of the travel times between two-adjacent stations of TransJakarta BRT[21]

到达车站的车辆等待乘客上下车，等待时间设置为服从三角分布的随机数，三角分布的最小值、最大值、众数分别为1 min、3 min、2 min.

包含1 000辆车的仿真时间为5 000 min.前50 min的仿真结果如图10所示.

图10（a）表示前9辆车的到达和离开，相应数据如表2所示，可以推算出停靠时间和车头时距.数据表明，第3辆车离开时第4辆车刚好到达，第4和第5辆、第6和第7辆、第7和第8辆也同样如此.因此，在第4、5、7、8辆车到达之前没有排队.由于车头时距较大，第一辆车载客人数的期望比其他车辆大.

表2 仿真中前9辆车的到达时刻、离开时刻、停靠时间及车头时距Table 2 The arrival,departure,dwell,and headway times of the first-nine buses on the simulation

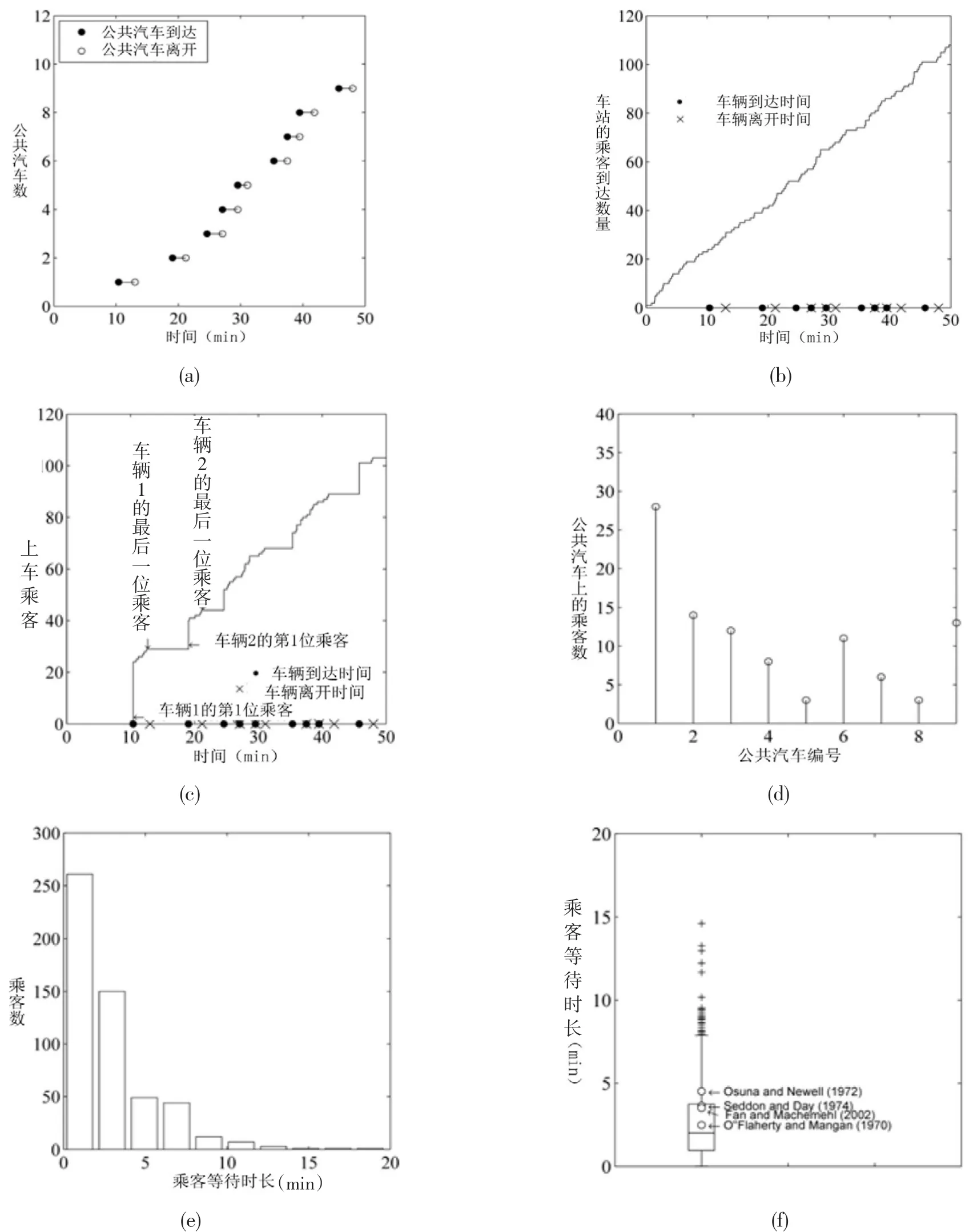
图10 仿真结果：(a)到达和离开车站的车辆数，仿真的前50 min结果；(b)乘客到达车站；(c)乘客上车；(d)乘客在车辆上；(e)乘客等待时间的分布；(f)乘客等待时间的箱线图，以及与一些数学模型的比较Fig.10 Simulation results:(a)Bus number arrived and left the station.Only the first 50-minute simulation time is shown;(b)The passengers arrived at the station;(c)The passengers boarding the buses;(d)The passenger on the buses;(e)The distribution of thepassenger waiting times;and(f)The boxplot of the passenger waiting times and its comparison to some mathematical models

图10（b）表示乘客到达车站数量随时间的分布，将此函数记为N() t，自变量仅有t≥0.明显看出，乘客的到达是一个平稳的泊松过程.图10（c）是乘客上车数量随时间的变化.在本案例中，前28位乘客上了第1辆车，其中有23位是在车辆来之前就在车站等待的乘客，5位是在车辆来的同时到达车站的.在图10（c）中，乘客的等待时间是一条长的垂直线，进一步说明了前述结论，即乘客在第4、5、7、8辆车之前不需要等待.图10（d）是前9辆车中乘客的数量.第1辆车载了28位乘客，是这些车辆载客人数中最多的，很好地印证了之前基于车头时距的观测结果.图10（e）是乘客等待时间分布.图10（f）是其箱线图形式的分布.箱线图与由式（1）至式（4）给出的等待时间的经验估计重叠，二者具有很强的一致性.事实上，4个模型求得的3个估计值大于仿真结果的中间值，并小于其上四分位数.

由这些试验得出结论：提出的乘客到达模型适用于模拟BRT车站乘客的到达.

3.2 简单通道

为数值试验建立一个较小的BRT对称网络.网络由一个停车场和两个BRT车站组成，BRT车站由两条路段连接.在仿真中，两辆车从停车场中出发进入网络.一旦车辆在网络中，就会从车站1行驶到车站2，然后从车站2行驶到车站1，循环往复.仿真事件模型如图11所示.

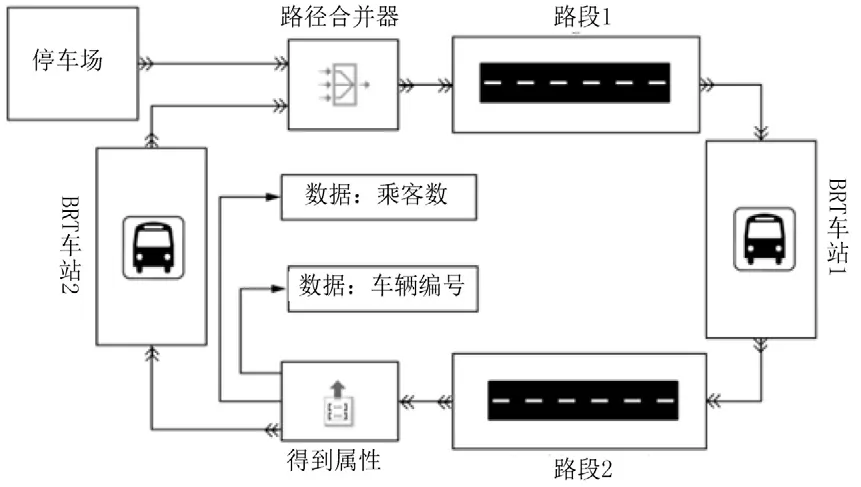
图11 两个车站的走廊的仿真模型Fig.11 The SimEvents-numerical model of the two-station corridor

除了路段子系统、停车场和BRT车站之外，上述仿真事件模型还包括其他子系统：路径组合和获取属性.前者允许车辆从停车场中或者从车站2行驶到路段1.后者允许提取车辆的内部数据或车辆的属性数据，包括车辆数量和车上的乘客数.

与仿真模型相关的完整模型参数如表3所示.这些参数包括BRT车站、路段、停车场.假设两个BRT车站完全相同，两条路段也完全相同.对于BRT车站，假设乘客到达服从平均到达率为1人/min的泊松分布，稍微小于Gunawan等[20]的研究结果；假设下车乘客数离散并均匀地分布在0至25人之间；车辆停靠时长约为2 min.对于路段，假设车辆行驶时间服从均值为5 min的指数分布，行驶时间的指数分布也由Gunawan等[21]研究得出.最后，根据高峰小时BRT发车频率标准，车辆的发车间隔设置为5 min[1].

表3 简单通道模型的参数Table 3 Parameters of the simple corridor model

图12 在200天重复试验中相对稳定情况下，两辆车上乘客时均数量的双边分布Fig.12 Bi-histogram of the distribution of the timeaveraged number of passengers on both the buses in steadystate condition for 200 replications

BRT系统通常每天运行18小时，本研究的仿真时长为24小时，试验重复200天.仿真结果如图12和图13所示.

图12是在稳定状态下，两辆车上乘客时均数量的分布.数据表现出了有趣现象，两辆车的乘客时均分布非常相似.鉴于模型的设计和输入参数都是对称的，这种现象是合理的.两辆车上的乘客数平均值为14，偏差为18.当车辆离开BRT车站2，85%的情况下有8位乘客上车，较少情况下第2辆车有大约60位乘客上车.第2辆车上的乘客数量变化范围很大，大约是第1辆车的两倍.

乘客数量的历史数据如图13所示，（a）是第1辆车，（b）是第2辆车.图右边是200天重复试验中乘客时均数量的最终状态.乘客数量通常在0至70之间波动.图中历史数据的描绘，对于车辆1，乘客62%的时间在车上，对于车辆2，乘客55%的时间在车上.

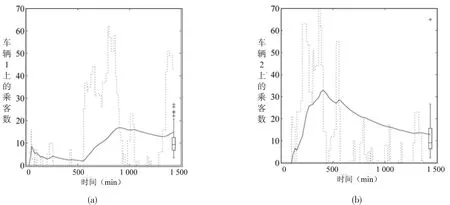
图13 车辆1和车辆2上的乘客数量（虚线），时均数量（实线），在最后分析中乘客时均数量的箱线图Fig.13 The history of the number of passengers on Buses 1 and 2(broken line),time-averaged(solid line),and a boxplot of the time-averaged number of passengers at the end of the analysis

4 研究结论

本文研究了仿真框架的应用潜力，建立了快速公交系统的动态仿真模型.框架建立在一般离散事件仿真系统的标准特征的基础上.对于这种特殊应用，BRT车站的建模较复杂，需要做出相关假设以方便系统开发.在数值试验中，较好地模拟了真实BRT系统的观测结果.

[1]Annie Weinstock,Walter Hook,Michael Replogle,et al. Recapturing global leadership in bus rapid transit:A survey of select U.S.cities[R].Technical Report,ITDP, May 2011.

[2]Carlos Campo.Bus rapid transit:Theory and practice in the United States and abroad[D].Master thesis,School of Civil and Environmental Engineering,Georgia Insti⁃tute of Technology,December 2010.

[3]Bus rapid transit in Brazil[R/OL].http://en.wikipedia.org/ wiki/Bus_rapid_transit_in_Brazil.Accessed on March2012.

[4]Fergyanto E Gunawan,Erwin Kusnandar.Evaluation of transjakarta performance in comparison with world class bud rapid transit(in Indonesian language)[J].Jurnal Ja⁃lan Dan Jembatan,2011,28(2).

[5]Sudarmanto Nugroho,Akimasa Fujiwara,Junyi Zhang. An empirical analysis of the impact of a bus rapid tran⁃sit system on the concentration of secondary pollutants in the roadside areas of the transjakarta corridors[J].Sto⁃chastic Environmental Research and Risk Assessment, 2011,25:655-669.

[6]Juha-Matti Lehtonen,Ulla Seppa.A methodology for da⁃ta gathering and analysis in logistics simulation project [J].Integrated Manufacturing Systems,1997,8(6):351-358.

[7]Huan Li,Baohua Mao,Robert L Bertini.Evaluating the impacts of bus facility design features on transit opera⁃tions in Beijing,China:A simulation approach[C].In 87th Annual Meeting of the Transp.Research Board, Jan.2008:13-17.

[8]G Alves,J Roßmann,R Wischnewski.A discrete-eventsimulation approach for logistic systems with real time resource routing and vr integration[J].World Academy of Science,Eng.,and Tech.,2009,58:821-826.

[9]A Visser,A J van der Wees,L O Hertzberger.Discrete event modelling methodology for intelligent transport systems[C].In Proc.of the World Congress on Intelli⁃gent Transport Systems,Torino,Italy,2000:2016.

[10]L V Bin,Niu Huimin.Realibility modeling and simula⁃tion of signalized intersections[J].Journal of Transporta⁃tion System Engineering and Information Technology, 2011,11(6):45-50.

[11]S Gao，Z Wu.Modeling passenger flow distribution based on travel time of urban rail transit[J].Journal of Transportation Systems Engineering and Information Technology,2011,11:124-130.

[12]Rodolfo Celestino Dos Santos Silva,Thiago Barros Brito, Rui Carlos Botter,et al.Modeling of a closed-loop mari⁃time transportation system with discrete event simula⁃tion and multi-criteria decision analysis[C].In Proc.of the World Congress on Eng.and Comp.Science,Vol⁃ume II,San Francisco,USA,Oct.2011:19-21.

[13]K Valiguran,M Foltin,M Blaho.Transport system real⁃izationinsimeventstool[R/OL].http://dsp.vscht.cz/ 20konference_matlab/MATLAB09/prispevky/107_vali⁃ gura.pdf,Accessed on March 2012.

[14]Transjakarta profile book[M].2012.

[15]C A O’Flaherty,D O Mangan.Bus passenger waiting times in central areas[J].Traffic Engineering and Con⁃trol,1970,11(9):419-421.

[16]Mir-Davood Salek,Randy B Machemehl.Characterizing bus transit passenger wait times.Technical Report Re⁃search Report 167211-1,Center for Transportation Re⁃search,June 1999.URL[R/OL].http://swutc.tamu.edu/ publications/technicalreports/167211-1.pdf

[17]Wei Fan,Randy B Machemehl.Characterizing bus tran⁃sit passenger waiting times[C].In 2nd Material Specialty Conference of the Canadian Society for Civil Engineer⁃ing,Montreal,Quebec,Canada,June 2002:5-8.

[18]Marco Luethi,Ulrich Weidmann,Andrew Nash.Passen⁃ger arrival rates at public transport stations.Institute for transport planning and systems,ETH Zurich,October 2006.URL[R/OL].http://www.andynash.net/nash-publi⁃cations/Luethi2007-pax-arrivals-TRB-paper.pdf.Re⁃trieved on July 2012.

[19]M K Islam,Upali Vandebona.Reliability analysis of pub⁃lic transit systems using stochastic simulation[C].In 33rd Australasian Transport Research Forum Confer⁃ence,Canberra,Australia,29 September-1 October, 2010.

[20]Fergyanto E Gunawan,Erwin Kusnandar,Bahtiar Saleh Abbas,et al.Empirical level of demand of transjakarta bus rapid transit[J].J.of Trans.Sys.Eng.and inf.Tech. (Review),2012.

[21]Fergyanto E Gunawan,Erwin Kusnandar,Bahtiar Saleh Abbas,et al.Travel time reliability of transjakarta,Indo⁃nesia bus rapid transit[J].J.of Trans.Sys.Eng.and Inf. Tech.(Review),2012

[22]E E Osuna,G F Newell.Control strategies for an ideal⁃ized public transportation system[J].Transportation Sci⁃ence,1972,21(1):55-61.

[23]E M Holroyd,D A Scraggs.Waiting times for buses in central London[J].Traffic Engineering and Control, 1966,8(3):158-160.

[24]P I Welding.The instability of a close-interval service [J].Operational Research Quarterly,1957,8(3):133-148.

[25]P A Seddon,M P Day.Bus passenger waiting times in greater Manchester[J].Traffic Engineering and Control, 1974,15:422-445.

Design and Implementation of Discrete-Event Simulation Framework for Modeling Bus Rapid Transit System

Fergyanto E.GUNAWAN
（Bina Nusantara University,Jakarta 11480,Indonesia）

ract:It is clear that bus rapid transit is a strong contender for the solution of massive traffic congestion faced by many cities across the globe.However,the success or failure of this system will depend on many variables such as service planning,infrastructure,station design,passenger information systems,and integration and access.In this work,we established a computational framework on the basis of the discrete-event system for modeling the bus rapid transit system.This particular development allowed us to cost-effectively evaluate the effects of some of those variables on BRT performance.The results were a few sub-systems that could directly be used to model a typical BRT system.Some limited numerical trials revealed that the developed sub-systems could reasonably reproduce phenomena commonly observed in an actual BRT system.

rds:urban traffic；discrete-event simulation；numerical model；traffic congestion；bus rapid transit

本文在离散事件仿真（Discrete-event Simulation,DES）的基础上，构建了一种快速公交系统的计算机仿真框架.与常规公交系统相比，快速公交系统具有独特的性质[1].构建的计算机框架是一组用于建立BRT系统仿真模型的子系统，这些子系统一般以DES系统的基本工具为基础.本文将对每个子系统的建立、设计和功能进行详细解释.

1009-6744（2014）04-0037-09

U491

A

2013-02-19

2013-06-25录用日期：2014-01-28

作者信息：Fergyanto E.GUNAWAN（1972-），男，博士，高级讲师. *

f.e.gunawan@gmail.com