Modeling and Optimization for Short-term Scheduling of Multipurpose Batch Plants*
2014-07-18CHENGuohui陈国辉YANLiexiang鄢烈祥andSHIBin史彬SchoolofMechanicalandElectronicEngineeringWuhanUniversityofTechnologyWuhan430070ChinaSchoolofChemicalEngineeringWuhanUniversityofTechnologyWuhan430070China
CHEN Guohui (陈国辉), YAN Liexiang (鄢烈祥)** and SHI Bin (史彬)School of Mechanical and Electronic Engineering, Wuhan University of Technology, Wuhan 430070, ChinaSchool of Chemical Engineering, Wuhan University of Technology, Wuhan 430070, China
Modeling and Optimization for Short-term Scheduling of Multipurpose Batch Plants*
CHEN Guohui (陈国辉)1, YAN Liexiang (鄢烈祥)2,** and SHI Bin (史彬)21School of Mechanical and Electronic Engineering, Wuhan University of Technology, Wuhan 430070, China2School of Chemical Engineering, Wuhan University of Technology, Wuhan 430070, China
In the past two decades, short-term scheduling of multipurpose batch plants has
batch plants, resource-task-network, unit-specific event, line-up competition algorithm, linear programming
1 INTRODUCTION
Multipurpose batch plants typically involve several processing units for producing many products with flexible production recipes and offer tremendous opportunities for improving productivity through scheduling of different operations. During the last two decades, the short-term scheduling of multipurpose batch plants has received considerable attention. This is motivated, on one hand, by the growing pressure to improve energy efficiency and reduce costs, and on the other hand, by the significant advances in relevant modeling and solution techniques and rapidly increased computational power.
Most scheduling problems are modeled using either state-task-network (STN) [1] or resource-task-network (RTN) [2] process representation. In contrast to the STN representation, RTN representation treats all the resources equally such as materials, processing and storage equipments, and utilities.
STN or RTN-based mathematical programming (MP) models can be classified into discrete-time and continuous-time models. Discrete-time models have two major disadvantages [3]. First, the size of mathematical model as well as its computational efficiency strongly depends on the number of time intervals. Second, sub-optimal or even infeasible schedules may be generated because of reduction of the domain of timing decisions. Due to these inherent limitations, continuous-time models have been developed for short-term scheduling of multipurpose batch plants in the past decade, in which events are potentially allowed to take place at any point in the continuous domain of time. The continuous-time models can be generally classified into three categories: slot-based [4-8], global event-based [9-12] and unit-specific event-based [13-20]. As shown in Fig. 1, in slot-based formulations, the time horizon is represented in terms of ordered blocks of unknown, variable length slots. Global event-based models use a set of events across all units, and the event point is defined for either the beginning or the end of each task in each unit. Unit-specific event-based models define events on a unit basis (non-uniform time grid), allowing tasks corresponding to the same event point but take place in different units at different time.
Most of these formulations applying continuoustime representation are based on either STN or RTN representation. Few formulations are based on both RTN representation and unit-specific events [18], in which continuous variable “finish time” was used. Since “finish time” can be expressed by continuous variables “start time”, the number of continuous variables and constraints in the model can be reduced. In order to explore the advantages of RTN and unit-specific events representation, an improved model for short-term scheduling of multipurpose batch plants under maximization of profit based on RTN and unit-specific events is proposed in this paper. A novel hybrid algorithm based on line-up competition algorithm and linear programming is applied to solve the model.
2 MODEL DEVELOPMENT
The short-term scheduling of multipurpose batch plants in this paper is as follows.
Given: (1) time horizon of operation; (2) RTN representation of processes; (3) processing time function of each task; (4) the maximum capacity of each equipment; (5) storage capacity (unlimited capacity in this study) and unit value of each material.
Determine: (1) resource equipment allocation foreach task; (2) amount of material in each task; (3) processing time of each task.

Figure 1 Concepts for continuous-time representation
2.1 Objective function
For the objective of maximum profit, the following formulation maximizes the amount of all material resources at the end of the last event point.

2.2 Constraints
2.2.1 Resource balances
At each event n, the amount of resource r equals the amount of resource r produced or consumed at event n and previous event n−1, and the amount of resource r at previous event n−1. The formulation can be written as

2.2.2 Capacity constraints
The amount produced by Task i at each event n is constrained by the lower and upper bounds on the capacity of corresponding units processing the material.

At each event n, the amount of resource r should between its lower and upper bounds.

2.2.3 Sequencing constraints
(1) Same task in the same unit
The start time of a task at the next event should be greater than the finish time of the same task at the current event.

(2) Different tasks in the same unit
In this paper, the changeover times are not considered.

(3) Different tasks in different units
For different tasks taking place in different units that either produce or consume the same material resource, the sequencing constraints are aligned as follows.

3 METHODOLOGY
3.1 Line-up competition algorithm
The line-up competition algorithm is an evolutionary algorithm [21, 22], but it is different from other evolutionary algorithms in nature. In the line-up competition algorithm, independent and parallel evolutionary families are always kept during evolution, each family producing offspring only by asexual reproduction. There are two levels of competition in the algorithm. One is the survival competition inside a family. The best one of each family survives in each generation. The other level is the competition between families. According to their values of objective function, families are ranked a line-up. The best family is in the first position in the line-up, while the worst family is in the final position. Families of different position have different driving forces of competition. The driving force of competition may be understood as the power of impelling family mutation. By competitions, the first family in the line-up is replaced continually by other families, or the value of its objective function is updated continually. As a result, the optimal solution is approached rapidly. The line-up competition algorithm has been applied to solve many difficult problems in theory and engineering, such as location-allocation [23], optimization of pressure relief header network [24], scheduling [25-27] and so on.
3.2 The hybrid algorithm
To solve the proposed mixed integer linear programming model, a novel hybrid algorithm based on line-up competition algorithm and linear programming is presented. The hybrid algorithm has two sides, inner side and outer side. Its basic idea lies in searching binary variables from the outer side by line-up competition algorithm, and solving the problem with linear programming in the inner side. The hybrid algorithm can be described as follows.
Step 1. Generate m families (parents) by producing m groups of binary variable randomly.
Step 2. Form m groups of linear programming problem according to the m groups of binary variable. Calculate the objective function values by solving m groups of linear programming problem.
Step 3. Rank m families to form a line-up according to the objective function values, with the line-up as a descending sequence for finding the global maximum.
Step 4. Decide the times of mutations based on the position of each family in the line-up, in which the first family has the fewest mutations, while the final family has the most mutations. Get m children from m parents.
Step 5. Calculate the objective function values for children and compare the values of children and parents for each family and better one survives as parent in the next generation.
Step 6. Repeat Steps 3-5 until reaching the specified evolutionary generations.
Step 4. The core of the hybrid algorithm. Its function is to balance local and global search. The first family in the line-up mutates only one time, which is beneficial to speed local search for finding optimal solution quickly, and the final family mutates many times, resulting in migration in a larger search space, which pays an important role in global search. The flowchart of the hybrid algorithm is shown in Fig. 2.
4 EXAMPLES
4.1 Description of examples
4.1.1 Eχample 1
This is a standard example for short-term scheduling of multipurpose batch plants [18]. Two products are produced through five stages: heating, reactions 1-3, and separation, as shown in the RTN representation of the plant flow sheet in Fig. 3. Since each of the reaction tasks can take place in two reactors, each reaction is represented by two separate tasks. The initial stock level for all intermediates is assumed to be zero. 4.1.2 Eχample 2
This is a more complex example [18], involving 11 tasks performed in 6 units processing 13 materials. The RTN for this example is shown in Fig. 4.
4.1.3 Relevant data for the eχamples
The relevant data for the examples is from [18]. Data of coefficients of processing time of tasks and limits on batch sizes of units are shown in Table 1. Data of capacities, initial amounts, and prices of different resources are shown in Table 2.
4.2 Results
The proposed model and hybrid algorithm are applied to the two examples, while the model is solved in GAMS distribution 21.1 using CPLEX 8.1.0 [18]. Figs. 5 and 6 compare the number of continuous variables in our models with that in [18] for Examples 1 and 2, respectively. The Gantt charts for Example 1 at H=8 and H=12 by this work are given in Figs. 7 and 8, respectively, and those for Example 2 at H=12 by this work are given in Fig. 9.

Figure 2 Flowchart of the hybrid algorithm

Figure 3 RTN representation for Example 1
The relatively detailed results by this work and those in [18] are shown in Tables 3 and 4. Our models have less continuous variables and constraints, reducing the searching space to some extent. For Example 1, the same optimal values are obtained, for Example 2, better optimal values are obtained in this work.
5 CONCLUSIONS
We investigate the RTN representation for unit-specific event-based models and propose an improved mixed integer linear programming model for short-term scheduling of multipurpose batch plantsunder maximization of profit, based on the model in [18]. To solve the model, a novel hybrid algorithm based on line-up competition algorithm and linear programming is presented. The performance of the proposed model and hybrid algorithm is evaluated with two examples in literature. The conclusions are as follows. (1) Compared with previous model [18], our models have less continuous variables and constraints, reducing the difficulty in solving the models; (2) for relatively simple problems such as Example 1, the same optimal values are obtained, while for more complex problems such as Example 2, better optimal values are obtained. The proposed model and hybrid algorithm are effective for short-term scheduling of multipurpose batch plants.

Figure 4 RTN representation for Example 2

Table 1 Data of coefficients of processing time of tasks, limits on batch sizes of units

Table 2 Data of capacities, initial amounts, and prices of different resources
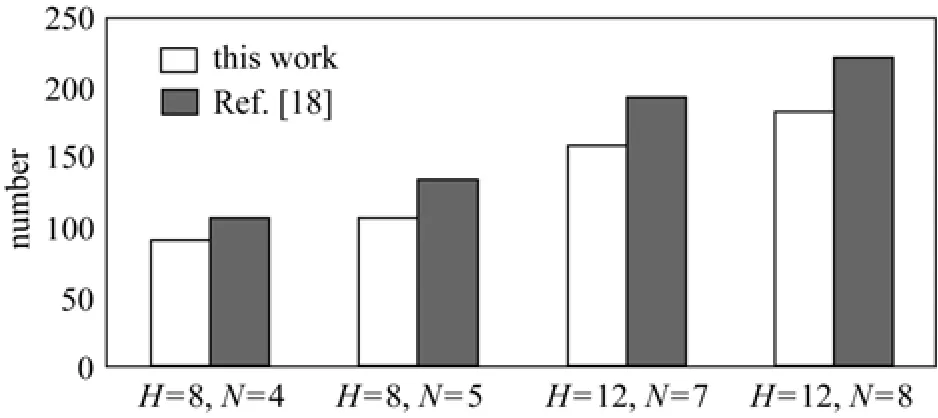
Figure 5 Comparison of the number of continuous variables for Example 1

Figure 7 Gantt chart for Example 1 by this work at H = 8 and N = 4

Figure 6 Comparison of the number of continuous variables for Example 2

Figure 8 Gantt chart for Example 1 by this work at H=12 and N=7

Figure 9 Gantt chart for Example 2 by this work at H=12 and N=7

Table 3 Comparison of the results for Example 1

Table 4 Comparison of the results for Example 2
NOMENCLATURE

REFERENCES
1 Kondili, E., Pantelides, C.C., Sargent, R.W.H., “A general algorithmfor short-term scheduling of batch operations—I. MILP formulation”, Comput. Chem. Eng., 17, 211-227 (1993).
2 Pantelides, C.C., “Unified frameworks for optimal process planning and scheduling”, In: Proc. Second Conf. on Foundations of Computer Aided Operations, Rippin, D.W.T., Hale, J., eds., CACHE Publications, 253-274 (1994).
3 Floudas, C.A., Lin, X., “Continuous-time versus discrete-time approaches for scheduling of chemical processes: a review”, Comput. Chem. Eng., 28, 2109-2129 (2004).
4 Pinto, J.M., Grossmann, I.E., “Optimal cyclic scheduling of multistage continuous multiproduct plants”, Comput. Chem. Eng., 18, 797-816 (1994).
5 Pinto, J.M., Grossmann, I.E., “A continuous time mixed integer linear programming for short term scheduling of multistage batch”, Ind. Eng. Chem. Res., 34, 3037-3051 (1995).
6 Karimi, I.A., McDonald, C.M., “Planning and scheduling of parallel semi-continuous processes. 2. short-term scheduling”, Ind. Eng. Chem. Res., 36, 2701-2714 (1997).
7 Lamba, N., Karimi, I.A., “Scheduling parallel production lines with resource constraints. 1. Model formulation”, Ind. Eng. Chem. Res., 41, 779-789 (2002).
8 Lamba, N., Karimi, I.A., “Scheduling parallel production lines with resource constraints. 2. Decomposition algorithm”, Ind. Eng. Chem. Res., 41, 790-800 (2002).
9 Zhang, X., Sargent, R.W.H., “The optimal operation of mixed production facilities—A general formulation and some approaches for the solution”, Comput. Chem. Eng., 20, 897-904 (1996).
10 Zhang, X., Sargent, R.W.H., “The optimal operation of mixed production facilities—Extensions and improvements”, Comput. Chem. Eng., 22, 1287-1295 (1998).
11 Wang, S., Guignard, M., “Redefining event variable for efficient modeling of continuous-time batch processing”, Ann. Oper. Res., 116, 113-126 (2002).
12 Castro, P.M., Barbosa-Povoa, A.P., Matos, H.A., Novais, A.Q.,“Simple continuous-time formulation for the short time scheduling of multipurpose batch plants”, Ind. Eng. Chem. Res., 43, 105-118 (2004).
13 Ierapetritou, M.G., Floudas, C.A., “Effective continuous-time formulation for short-term scheduling: 1. Multipurpose batch processes”, Ind. Eng. Chem. Res., 37, 4341-4359 (1998).
14 Lin, X., Floudas, C.A., “Design, synthesis and scheduling of multipurpose batch plants via an effective continuous-time formulation”, Comput. Chem. Eng., 25, 665-674 (2001).
15 Lin, X., Chajakis, E.D., Floudas, C.A., “Scheduling of tanker lightering via a novel continuous-time optimization framework”, Ind. Eng. Chem. Res., 42, 4441-4451 (2003).
16 Shaik, M.A., Janak, S.L., Floudas, C.A., “Continuous-time models for short-term scheduling of multipurpose batch plants: A comparative study”, Ind. Eng. Chem. Res., 45, 6190-6209 (2006).
17 Shaik, M.A., Floudas, C.A., “An improved unit-specific event-based continuous-time model for short-term scheduling of continuous processes: Rigorous treatment of storage requirements”, Ind. Eng. Chem. Res., 46, 1764-1779 (2007).
18 Shaik, M.A., Floudas, C.A., “Unit-specific event-based continuous-time approach for short-term scheduling of batch plants using RTN framework”, Comput. Chem. Eng., 32, 260-274 (2008).
19 Li, J., Susarla, N., Karimi, I.A., Shaik, M.A., Floudas, C.A., “An analysis of some unit-specific event-based models for the short-term scheduling of noncontinuous processes”, Ind. Eng. Chem. Res., 49, 633-647 (2010).
20 Vooradi, R., Shaik, M.A., “Improved three-index unit-specific event-based model for short-term scheduling of batch plants”, Comput. Chem. Eng., 34, 148-172 (2012).
21 Yan, L., “A new global optimization search algorithm for process system”, Ph. D. Thesis, Beijing Univ. Chem. Tech., Beijing (1998). (in Chinese)
22 Yan, L., Ma, D., “Global optimization of nonconvex nonlinear programs using line-up competition algorithm”, Comput. Chem. Eng., 25, 1601-1610 (2001).
23 Yan, L., Shen K., Hu, S., “Solving mixed integer nonlinear programming problems with line-up competition algorithm”, Comput. Chem. Eng., 28, 2647-2657 (2004).
24 Yan, L., “Solving combinatorial optimization problems with line-up competition algorithm”, Comput. Chem. Eng., 27, 251-258 (2003).
25 Chen, G., Shi, B., Yan, L., “Multi-period optimal operational planning of boiler steam system based on line-up competition algorithm”, Energy Procedia, 14, 613-619 (2012).
26 Shi, B., Yan, L., “Scheduling of multi-purpose batch process with parallel units”, CIESC Journal, 61, 2875-2880 (2010). (in Chinese)
27 Shi, B., Yan, L., Wu, W., “Rule-based scheduling of single-stage multiproduct batch plants with parallel units”, Ind. Eng. Chem. Res., 51, 8535-8549 (2012).
2013-08-15, accepted 2013-09-23.
* Supported by the National Natural Science Foundation of China (21376185) and the Fundamental Research Funds for the Central Universities (WUT: 2013-IV-032).
** To whom correspondence should be addressed. E-mail: hgxtgc@163.com
significant attention. Most scheduling problems are modeled using either state-task-network or resource-task-network (RTN) process representation. In this paper, an improved mixed integer linear programming model for short-term scheduling of multipurpose batch plants under maximization of profit is proposed based on RTN representation and unit-specific events. To solve the model, a hybrid algorithm based on line-up competition algorithm and linear programming is presented. The proposed model and hybrid algorithm are applied to two benchmark examples in literature. The simulation results show that the proposed model and hybrid algorithm are effective for short-term scheduling of multipurpose batch plants.
杂志排行
Chinese Journal of Chemical Engineering的其它文章
- Roles of Biomolecules in the Biosynthesis of Silver Nanoparticles: Case of Gardenia jasminoides Extract*
- A LCA Based Biofuel Supply Chain Analysis Framework*
- Symbiosis Analysis on Industrial Ecological System*
- Phase Behavior of Sodium Dodecyl Sulfate-n-Butanol-Kerosene-Water Microemulsion System*
- Photochemical Process Modeling and Analysis of Ozone Generation
- Unified Model of Purification Units in Hydrogen Networks*
