北斗信号捕获相位相干算法的设计与实现

黄海生， 李龙龙

( 西安邮电大学 电子工程学院， 陕西 西安 710121)

北斗信号捕获相位相干算法的设计与实现

黄海生， 李龙龙

( 西安邮电大学 电子工程学院， 陕西 西安 710121)

针对北斗二号卫星导航系统信号捕获运算量大的问题，提出一种利用相位相干算法搜索起始码相位的方法，并给出基于现场可编程门阵列(FPGA)的相位相干算法的具体实现方案，算法中关于旋转因子运算的问题主要借助坐标旋转数字计算方法和查找表方法得以解决。编译综合及仿真结果皆表明，与传统快速傅里叶变化(FFT)算法相比，新方法只需用到复数加法，运算量小，且能正确捕获信号。

相位相干算法;旋转因子;现场可编程门阵列(FPGA);坐标旋转数字计算方法(CORDIC)

北斗卫星导航系统是我国正在实施自主研发和独立运行的全球卫星导航系统，它在亚太地区已经初步形成了导航、授时和精密定位能力，应用服务已经扩展到交通运输、测绘、气象等相关领域。 传统的北斗信号捕获广泛采用快速傅里叶变化(Fast Fourier Transform，FFT)获得信号的初始码相位，但随着科技技术的快速发展，对于北斗信号的快速捕获提出了更高标准的要求，传统捕获方法运算量相对较大, 而且捕获时间受限制, 为了适应工作在高动态环境下的要求, 有人提出了相位相干捕获算法[1]。该算法在搜索伪随机码的相关峰值上比传统的FFT算法运算量更少，当序列长度变大时，其优越性更加明显。

本文拟基于现场可编程门阵列(Field-Programmable Gate Array，FPGA)芯片，利用硬件描述语言实现相位相干算法的设计，根据算法的设计流程，对定点数位数调整来更好地达到设计精度要求。利用存储器对数据中间值的存储，最终获得码起始相位值。

1 相位相干算法及其实现方式

1.1 相位相干算法

相位相干算法的设计流程主要包括序列分割、相位相干和多层相位相干3部分。序列分割是将长度均为N=RC的本地序列L和接收序列R，皆分割成长度为C的R个子序列。相位相干将R个子序列转换成R个幅度值和R个角度值的过程，其值用于序列所在行和列的计算。多层相位相干是根据运算的需求以及子序列长度的满足，对相位相干计算中得到的行值m所对应长度为C的子序列再次进行序列分割和相位相干的计算，最终根据行和列的值得到接收序列的起始相位值。

1.2 实现方式及运算精度

采用定点数实现算法的运算[2]。

由于考虑到运算过程中误差值的累积和中间值的变化，为达到设计中运算精度的要求，所以将数值保留到小数点后4位。在设计中将相位角比特位设置为27位,其中1位符号位，9位整数位，17位小数位。幅度比特位设置为22位，其中1位符号位，6位整数位，15位小数位。借助Matlab内部自带的函数fi对数据进行量化并编码。fi函数表达式为fi(a，b，c，d)，其中a代表需要量化的数据，b代表符号位位数(默认取值为1)，c代表数据的总位数，d代表小数位数。

2 基于FPGA的算法设计与仿真

根据伪随机码的产生原理[3]，利用FPGA生成北斗卫星B1频点的普通测距码(C码)作为本地序列L,并将序列L进行相应的移位作为输入序列S,然后通过相位相干算法对两组输入的序列进行相应处理，对于过程中的指数运算均采用坐标旋转数字算法(Coordinate Rotation Digital Computer，CORDIC)来实现[4]，运算过程中的中间结果利用随机存取存储器(Random Access Memory, RAM)来存储[5]，通过各模块的层层运算，最终得出输入序列的码起始相位值。总体设计如图1所示。

图1 基于FPGA的算法总体设计

2.1 北斗卫星C码产生器

B1频点C码产生器是由两个长度为11位的反馈移位寄存器G1和G2构成的，经模2产生平衡Gold码，再截断1码片，生成码长为2046 chips，速率为2.046 MHz，周期为1 ms的普通测距码。反馈电路由模2加法器实现，G1对应于特征多项式

1+x+x7+x8+x9+x10+x11，

G2对应于特征多项式

1+x+x2+x3+x4+x5+x8+x9+x11。

两者皆在同一个时钟频率2.046 MHz下工作，两个移位寄存器的初值均为“01010101010”，且被预先置入寄存器。

通过对产生G2序列的移位寄存器不同抽头的模2和可以实现G2序列相位的不同偏移，同G1序列模2后生成不同卫星的测距码。卫星ID的确定是通过G2寄存器的两个输出位置来决定的。

B1频点C码产生器原理图如图2所示。

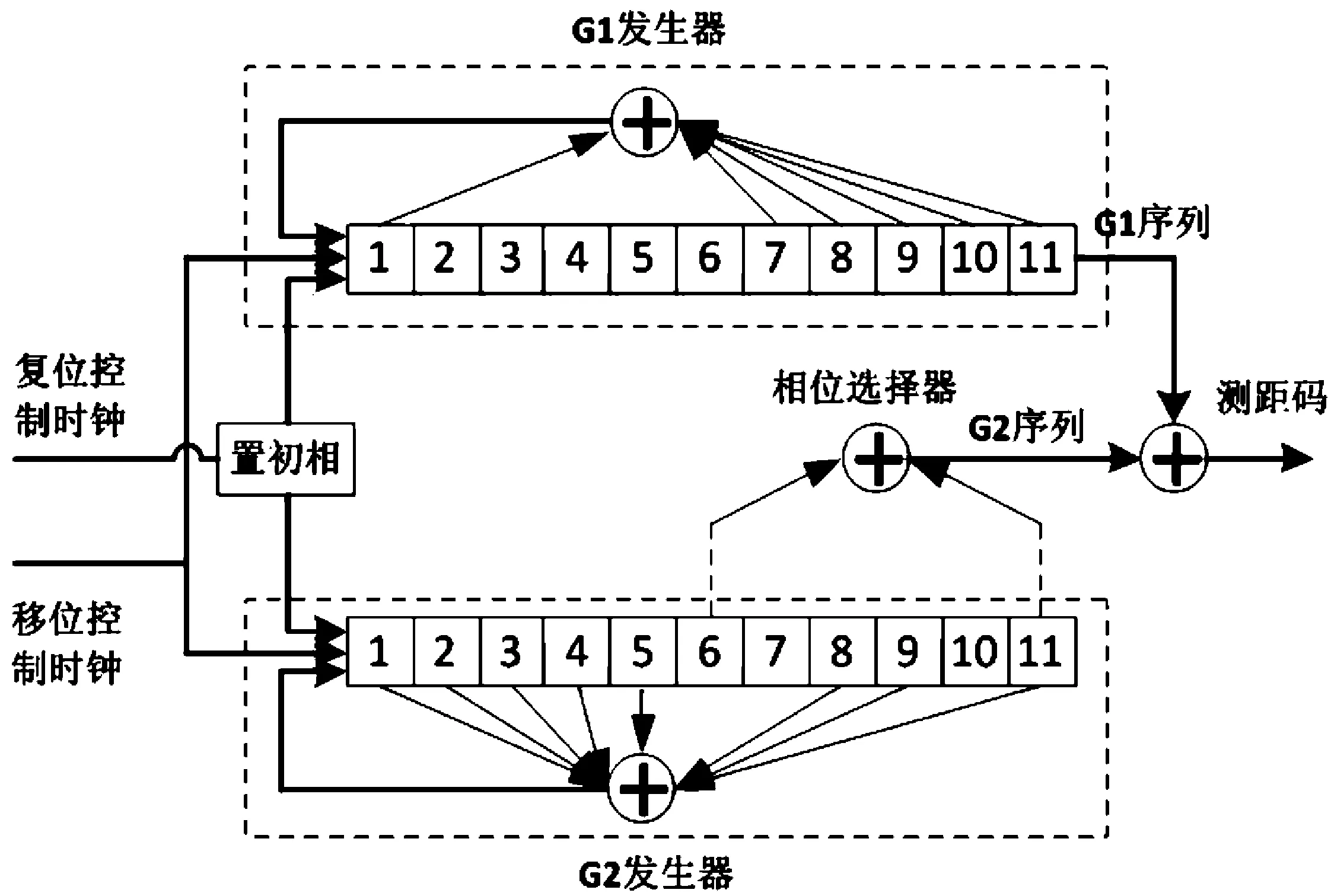
图2 B1频点C码产生器原理

2.2 序列分割模块

根据输入序列进行相应分割。考虑到B1频点中C码的序列长度N=2046，故取R=33和C=62对序列进行分割。

在系统时钟的节拍下，先进行列输入，当计数器值为32时，进行清零，并进入下一列，直到将2046个码片分割完。最终产生两组存储深度均为33的62位本地存储器L和接收存储器R。

2.3 初始化只读内存模块

WC=exp( 2jπ/C)，

而旋转因子指数p的取值范围为0～C-1。

由于C已知，所以利用Matlab生成旋转因子的实部real和虚部imag的浮点值[7]，利用函数fi(a,1,22,15)(其中a取实部或虚部的浮点值)进行量化并编码为22 bits的定点数，最终初始化为相应的ROM表,模块输出宽度均为22位的re[n]和im[n](n=0,1,…,33)。

2.4 判决及叠加模块

由于C码产生器输出的有一定周期取值是0和1的离散码序列，通过判决L和R中每个数据比特位的值对相应的re[n]和im[n]值进行加减。部分Verilog相关代码如下。

if(L[m][n]==1)

begin

L_re[m]<=L_re[m]+re[n];

L_im[m]<=L_im[m]+im[n];

end

else

begin

L_re[m]<=L_re[m]-re[n];

L_im[m]<=L_im[m]-im[n];

end

2.5 CORDIC算法向量模式

CORDIC算法向量模式流水线结构主要由寄存器、移位器和加减法器构成[2]，结构如图3所示。

图3 CORDIC算法向量模式流水线结构

将所输入的实部和虚部数据从直角坐标转换为极坐标，即可得到相应的相位幅度和相位角。部分Verilog实现代码如下。

if(y_in[21]～^x_in[21]==0)

begin

x_out<=x_in-(y_in>>>N);

y_out<=y_in+(x_in>>>N);

z_out<=z_in-SITA;

end

else

begin

x_out<=x_in+(y_in>>>N);

y_out<=y_in-(x_in>>>N);

z_out<=z_in+SITA;

end

最终所得到的z_out为相位解真值， 而x_out是将相位幅度真值放大Kn(畸变因子)倍后的值。在计算中，取迭代次数N=16可得畸变因子

如果计算中需要真实相位幅度，就需对x_out进行除Kn校正。最后，根据输入的实部和虚部的符号位，对相位角进行相应的处理，将角度范围调整为[-π，π]。图4是在x_in和y_in的输入值均为-0.707 1的情况下，输出结果的仿真图。

图4 相位和幅度输出结果仿真

2.6 复数相位计算模块

复数相位计算模块实际上就是一个减法器，根据所在行值y∈(0,32)的不同,当0≤i≤32-y时，计算

L_phase[i]-R_phase[i+y],

当33-y≤i≤32时，计算

L_phase[i]-R_phase[i+y]-(360/62)，

最终可以得到33×33=1 089个相位角值。

2.7 CORDIC算法旋转模式

CORDIC算法旋转模式结构与向量模式一样。不同点在于将所输入的相位角度转化为角度正弦和角度余弦。首先，对所输入的相位角进行象限标记；其次将其修正在[0，π/2]范围之内。最后，根据象限标记对正弦值和余弦值进行相应的修正。图5是相位角为225°时输出结果仿真图。

图5 正弦和余弦的输出结果仿真

2.8 累加模块

累加模块的主要功能是将产生的1 089对C_real和C_imag，经过累加产生33对sum_real和sum_imag。

2.9 判决及C码起始相位计算模块

该模块首先对所得到的R个相位幅度进行判决，如果存在其值等于R，从而得到该值所在的行d，那么说明搜索成功，反之亦然。当搜索成功时，C/A码起始相位计算模块根据该相位幅度所对应的相位角计算出所在的列c。最后，根据

out=C×R+d

计算出C/A码的起始相位值。

2.10 设计结果仿真与结果分析

根据N=2 046，故而R和C分别取值为33和62。产生一个本地序列L，将本地序列进行随机循环移位后作为输入序列S，利用Modelsim进行相关仿真。移位0位和左移1 022位后搜索到最大幅度值max_mag及其所对应的相位值max_mag_phase的仿真结果分别如图6和图7所示。由结果可知，设计模块搜索到正确峰值(由于设计中d值是从0开始的，所以对结果进行了加1修正)。

图6 零移位Modelsim仿真结果

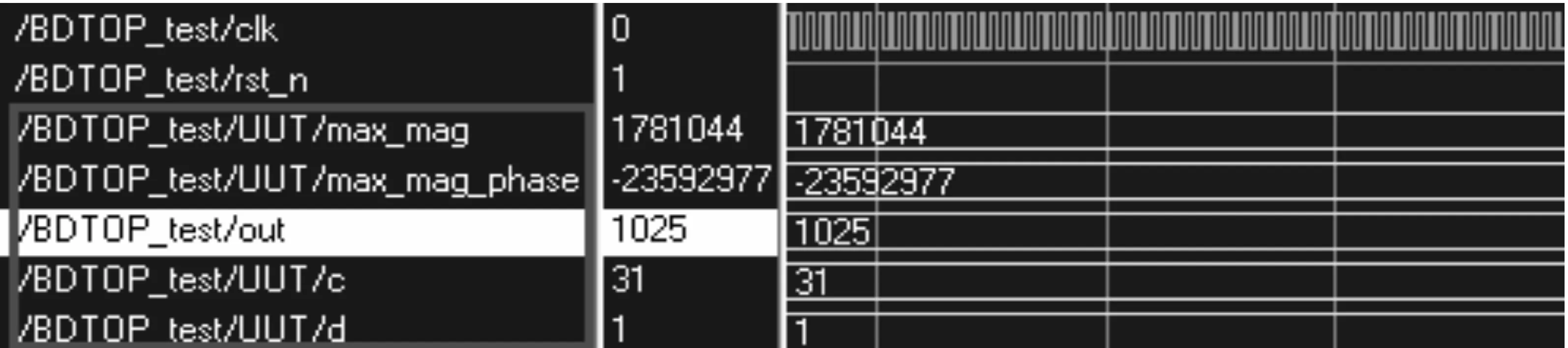
图7 左移1 022位Modelsim仿真结果

3 实际资源使用

通过选用Altera公司生产的cyclone II系列的 EP2C35F672C6芯片，在Quartus II 9.0的开发环境下对代码进行编译综合，使用资源情况报告如图8所示。

图8 资源使用报告

4 结语

实现了对码相位相干算法的FPGA设计，采用CORDIC算法，并应用定点数以满足算法的设计要求。仿真验证结果表明，设计达到预期目的，此设计可用于北斗卫星信号伪随机码的捕获。

[1] Chang Chieh-Fu, Hsieh Wan-Hsin, Kao Ming-Seng. A Novel Computationally Efficient Code Phase Acquisition Method[C]//Proceedings of the 24th International Technical Meeting of the Satellite Division of the Institute of navigation. Portland,Oregon, USA: ION GNSS 2011, 2011:2114-2116.

[2] 田耘,许文波,张延伟.无线通信FPGA设计[M].北京：电子工业出版社,2007：81-137.

[3] 崔保延. GPS软件接收机基础[M]. 2版. 陈军,潘高峰,译.北京：电子工业出版社,2007：63-87.

[4] 杨宏,李国辉,刘立新.基于FPGA的CORDIC算法的实现[J].西安邮电学院学报,2008,13(1)：75-77.

[5] 夏雨闻.Verilog数字系统设计教程[M].2版.北京：北京航天大学出版社,2008：27-115.

[6] 高西全,丁玉美.数字信号处理[M].3版.西安：西安电子科技大学出版社,2008：110-120.

[7] 刘卫国.MATLAB程序设计与应用[M].2版.北京：高等教育出版社,2006：17-80.

[责任编辑:王辉]

Design and implement of Beidou signal acquisition phase coherence algorithm

HUANG Haisheng, LI Longlong

(School of Electronic Engineering, Xi’an University of Posts and Telecommunications, Xi’an 710121, China)

A method using Phase Coherence Algorithm to search initial code phase is proposed for the large signal acquisition and computation on BeiDou II Navigation Satellite System. A specific implementation scheme based on Field-Programmable Gate Array (FPGA) of Phase Coherence Algorithm is given accordingly. It mainly use Coordinate Rotation Digital Computer (CORDIC) algorithm and look-up table method to solve the twiddle factor operation problems in the algorithm. This method is validated on the cyclone II series FPGA of Altera. Simulation results show that compared to the traditional Fast Fourier Transform (FFT) algorithm, this method can greatly reduce computation and can correctly acquire signal by only using the complex addition.

phase coherence algorithms, twiddle factor, field-programmable gate array(FPGA), coordinate rotation digital computer(CORDIC)

10.13682/j.issn.2095-6533.2014.01.005

2013-09-27

陕西省科技统筹创新工程计划战略基金资助项目(2012KTCQ01-06);陕西省教育厅服务地方专项基金资助项目(2013JC10)

黄海生(1964-)，男，教授，从事专用集成电路设计研究。E-mail: hhs@xupt.edu.cn 李龙龙(1988-),男，硕士研究生，研究方向为专用集成电路设计。E-mail: 363732023@qq.com

TN492

A

2095-6533(2014)01-0026-05