计算机辅助公差设计的开发及应用*

魏建东，李静蓉，苏杭朋

(华南理工大学 机械与汽车工程学院 广州 510641)



计算机辅助公差设计的开发及应用*

魏建东，李静蓉，苏杭朋

(华南理工大学 机械与汽车工程学院 广州 510641)

针对目前计算机辅助公差设计软件的操作繁杂并且缺少装配尺寸链分析的现状，搭建了面向公差设计的装配信息数据结构,便于进行公差设计分析；在优化装配尺寸链生成算法的基础上，运用蒙特卡罗法进行公差分析，在主流的三维造型软件Creo平台上二次开发出了一套基于装配尺寸链自动生成的计算机辅助公差设计软件模块，并以实例验证了实用性。

计算机辅助公差设计；装配尺寸链；Creo二次开发；蒙特卡罗

0 引言

计算机辅助公差设计(Computer Aided Tolerancing，简称CAT)[1]是指在机械产品的设计阶段利用计算机对产品的尺寸公差进行优化，以制造出满足精度要求的产品。将CAT中的装配尺寸链自动生成技术运用到产品的虚拟装配检测阶段，可以提前检测到装配干涉，及时地根据装配尺寸链封闭环的精度要求对装配零部件进行公差分析和公差分配。在产品设计过程中, 装配尺寸链不仅仅是确定零件制造公差的依据, 也是分析预测机械产品装配精度的依据; 在产品生产过程中, 装配尺寸链还是处理零件加工质量和产品装配质量的依据。因此基于装配尺寸链的公差设计是实现产品顺利加工制造、装配的关键。

然而由于现代产品设计中装配结构的日趋复杂，尺寸链数目和每个尺寸链中包含的组成环数目繁多，再加上各尺寸之间关系、装配约束关系的多样性，完全依靠人工来建立尺寸链图、尺寸链方程并求解, 整个过程将会非常繁琐和易出错。为此, 通过三维CAD平台软件的功能开发，直接从CAD装配模型中求解封闭环,以实现计算机辅助公差设计，具有高效、可靠的优点，有助于提高制造业的生产效率。

本文在分析尺寸链自动生成[2-3]关键技术的基础上，基于Creo软件平台，开发出了一个简捷、实用的公差分析模块，并集成蒙特卡罗法[4]对尺寸链进行分析计算。下面是对尺寸链的自动生成的关键技术的分析。

1 面向公差设计的装配信息数据结构搭建

1.1 装配约束特征信息的筛选和提取

特征信息提取的目的是为其他应用领域准备数据，在 VC++开发环境下，采用面向对象方法，搭建面向公差设计的装配信息数据结构。在Creo设计环境下建立的三维零件模型，需要获取其特征信息需要使用二次开发手段，本文应用Creo Parametric Toolkit 库函数ProSolidFeatVisit实现特征提取，过程如下图1所示：

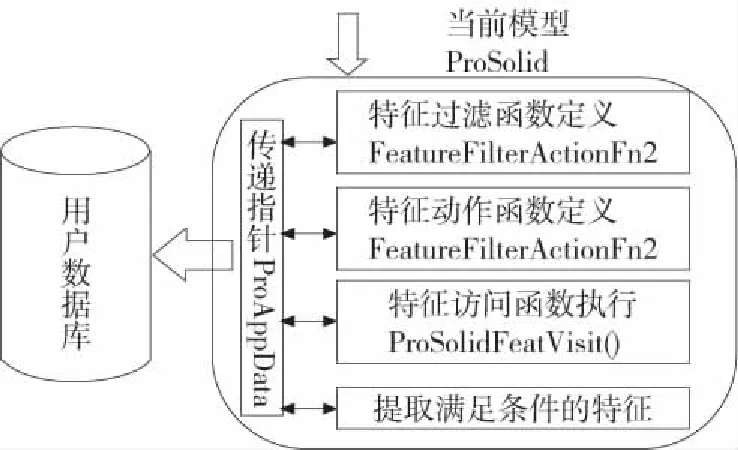
图1 约束特征提取

在CAD软件中，要确定零件在装配体中的位置和自由度，必须施加多个约束关系来实现对零件的定位；而对于已确定的装配尺寸链，只是要求装配体在某个方向或某个平面内的尺寸[5]。因此，对于装配尺寸链来说，装配体中的约束数据信息存在大量的多余信息。这些与装配尺寸链无关的约束条件，增加了搜索算法的复杂度，并且容易出错，极大的阻碍了装配尺寸链的自动生成，所以要提取满足装配尺寸链封闭环相关条件的特征信息，就要过滤掉干扰约束特征。

Creo中提供了多种装配约束条件，如对齐、对齐-偏移、匹配、匹配-偏移、相切、插入等。不同的约束条件参与约束的特征不同，因而判断其是否冗余的方式不同，本文主要是通过约束特征面向量与封闭环特征端面向量进行比较，实现冗余约束特征的判断。以下是常用约束配合的判定方法：

利用Creo Parametric Toolkit 库函数ProAsmcompconstraintTypeGet()获取装配约束类型。

(1)若约束为匹配或对齐配合：参与配合的特征为曲面，可以利用函数ProSurfaceXyzdataEval()获取配合特征面的法向量，将该向量与封闭环起始端面法向量点乘，若乘积为零，则表明两平面垂直；根据装配约束可知，该特征面与封闭环没有尺寸约束关系，因而可以过滤掉；反之，则保留该约束；

(2)若约束为插入配合：参与配合的特征一般为轴线，可以利用函数ProAxisDataGet()获得轴线向量，处理方法同(1)；

(3)若约束为相切配合：参与配合的特征一般为曲面或者柱面，可利用函数ProSurfaceParamEval()获取曲面在切线或者切点的法向量，处理方法同(1)；将上述方法在特征过滤函数FeatureFilterActionFn2()中实现，可以将大部分与封闭环无关的配合特征面排除，再通过特征访问动作函数FeatureVistiActionFn2()将满足以上条件的特征面保存在传递指针ProAppData中，供后续装配尺寸链自动生成调用。

1.2 数据库搭建

采用合理的数据结构提取和存储装配约束信息，是生成装配尺寸链进而进行公差设计的关键。因此搭建的面向公差设计的数据库要利于进行公差设计。本文在分析三维模型数据表达的基础上结合Creo Parametric Toolkit 二次开发工具搭建了元件尺寸数据库和装配约束数据库，各数据结构的具体定义可参考文献。

基于Creo的三维信息模型表达，描述零件尺寸信息的用户数据结构如下：

Typedef struct User_Dim_Database

{ProDimension *dimension;//尺寸对象指针

int id;//元件标识

ProMdl owner;//尺寸所属零件

double *value;//尺寸值

double *upper_limit//上偏差

double *lower_limit//下偏差

}userDimDatabase；

三维装配模型中，组件是几个零件根据不同的装配约束关系和装配序列装配起来的，装配尺寸链是有几个参与装配约束的零件构成的，采用遍历算法可以提取到所有约束的数据信息，为后续的装配尺寸链生成提供便利。具体的用户装配约束数据结构如下：

Typedef struct User_Constr_Database//用户装配约束数据结构

{ProAsmcompconstraint constr_array;//约束句柄

ProAsmcompConstrType type;//约束类型ProSelection comp_constr,asm_constr;

//约束的两个面

ProMdl comp_constr_owner,asm_constr

_owner;//所属零件

int id1,id2; //所属零件标识

} userConstrDatabase;

2 公差设计模块功能实现

2.1 装配尺寸链自动生成算法

装配尺寸链的自动生成是计算机辅助公差设计的基础。其目标在于，从装配约束数据库中除去干扰约束特征，并根据尺寸链生成最短原则和封闭原则更新装配约束数据库[6]。

2.1.1装配约束链的生成

装配尺寸链生成之前先要通过人机交互，人工选择出封闭环的起始端面。装配约束链的生成是在装配约束数据库中，从封闭环特征面开始查找和封闭环相互关联的特征面。装配约束链的查找过程如下:

①在装配约束数据库中(1.2中搭建的已经经过筛选的数据库)查找与封闭环起始端面属于同一零件的特征约束面；②根据装配约束条件，映射到与该特征约束面相配合的约束面。判断该特征面是否为封闭环的结束端，或者和封闭环的终止端属于同一零件，若是则可以结束搜索过程，若不是则将该特征约束面定义为新的封闭环起始端；③重复①和②的查找过程，直到找到所需的全部特征约束面；④依次记录查找所有经过的特征约束面和约束条件，所得数组即为装配约束链。通过以上流程，装配约束面的信息都保存在链表数组中，各个元素即为组成封闭环的要素。

假定封闭环的特征元素为面，装配模型也可以简化为图2所示。

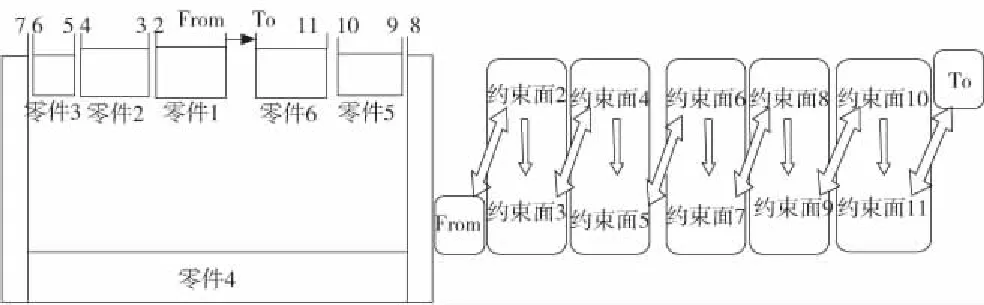
图2 装配模型

封闭环的起始为From特征面，约束面2、3属于同一个约束类型下的两个参考面；约束面3、4属于同一个零件。根据起始位置遍历搜索参与装配尺寸链的约束类型，从装配信息约束数据库中提取需要的特征面信息，按照上文介绍的搜索算法依次搜索到各个特征面并将其存储在定义的链表数组中。链表数组中的元素依次为：约束面2、约束面4、约束面6、约束面8、约束面10。

2.1.2 公差设计函数的表达

目前公差的解算和优化问题基本上是基于尺寸链建立公差设计函数的数学模型, 然后进行数学求解和优化。因此在装配约束链生成之后，要实现公差设计函数的表达。

公差设计函数是关于封闭环与各个组成环之间关系的函数，可表示为：

A0=f(A1,A2,...,An-1,An)

(1)

其中，A0为封闭环，A1,A2,An-1,An为组成环。为了表述封闭环对组成环的敏感程度引入了传递系数ξ的概念[7]。则组成环Ai的传递系数为：

(2)

将式(1)展开，得到式(3)如下：

A0= f(A1,A2,...,An) = ξ1· A1+ ξ2· A2+…+ ξn· An

(3)

其中ξi表示各组成环i的传递系数。

由式(3)可以看出，公差设计函数确定的关键是计算各组成环的传递系数。

对于线性尺寸链的传递系数只有1或者-1。本文对组成环传递系数的计算采用矢量判断方法，根据选择的封闭环的先后顺序确定搜索方向(如下图3)，再根据装配约束链表中顺序确定各个组成环的矢量方向，与封闭环对比即可得出各个组成环的传递系数。按照所述传递系数判断方法计算，图3的尺寸链表达函数为：A0== -A1+A2-A3-A4。

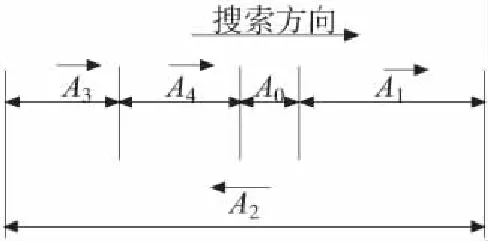
图3 尺寸链增减环判断

2.2 公差分析中的蒙特卡罗模型建立

公差分析与综合涉及到公差分配、公差校验以及公差优化等问题。这方面主要有极值法、概率统计法、加工成本- 公差模型、基于变动几何的公差设计函数、基于二阶和四阶可靠性指标的公差优化设计模型、敏感分析法、百分比贡献分析法、基于蒙特卡罗法的公差优化设计模型等方法[1]。本文将极值法、概率统计法和蒙特卡罗法集成于公差设计分析模块。

基于蒙特卡罗法求解装配尺寸链的思想就是模拟一批零部件随机装配所测得封闭环的实际尺寸。根据组成环尺寸的分布形式随机取样，把由抽样得到的尺寸数值带入到公差设计函数中，求解得到一个封闭环尺寸值，将此过程重复多次得到多个封闭环尺寸值，即可根据这些值估计出封闭环的公差。

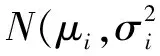
1)利用计算机产生一系列的(0，1)均匀分布的伪随机数ri，再进行坐标变换转化成服从N(0,1)分布的随机数，变换公式[9]为：

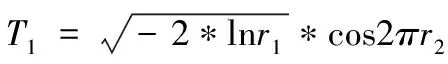
(4)

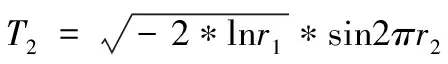
(5)

ai=Ai′ +Tiσi

(6)

式中：Ai′是第i个尺寸有公差带中心算起的公称尺寸Ai′=(Aimax+Aimin)/2；ai要在3σ范围内截尾，因此剔除T±3σ以外的随机数。

3)根据式(3)将组成环尺寸随机抽样的各随机变量带入到尺寸链方程中，则可以求得一个封闭环尺寸A0，经过反复计算N次求得一系列的尺寸A0 i，i=(1,2,3,...N)，根据封闭环尺寸的分布可以求得其特征量—均值和方差 ，封闭环的公称尺寸和公差，及其最大值和最小值。在置信水平1-α下，封闭环尺寸公差A0在抽样最大值A0max和最小值A0min之间的概率不小于P时，随机模拟抽样次数N即最小样本容量，可以有下式求出[9]：

NPN-1-(N-1)PN-α=0

(7)

在运用蒙特卡罗法进行公差分析时，实际抽样次数必须大于根据式(7)算出抽样次数N。

3 实例分析

如图4简化放大的双联齿轮，为了保证齿轮能够在轴上自由的旋转，并且在轴向方向没有太大的移动。就是要保证齿轮右端面和右侧挡环的左端面具有一定的间隙，即A0的尺寸是该结构的主要保证尺寸。尺寸过小的话，会引起较大的摩擦，不利于齿轮转动；尺寸过大的话会引起齿轮的啮合齿宽变小，造成传动不平稳。因此采用本文开发的模块对此模型公差进行分析。

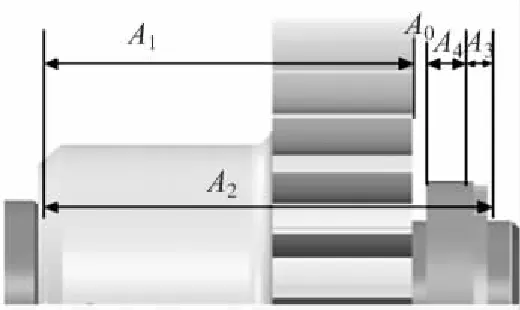
图4 实例模型

装配尺寸链生成的人机交互过程如下：

Step1：选择齿轮的右端面和右挡环的左端面作为封闭环；点击选择封闭环按钮完成如下功能：①尺寸链组成环的查找；②剔除多余环节(将参与多个装配的无关约束剔除)。

Step2：点击查找组成环按钮，完成对组成环信息显示存储,并高亮显示约束，如图5所示。

图5 装配尺寸链生成向导

Step3：选择生成尺寸链按钮，完成尺寸链表达函数建立；通过尺寸链生成向导获得各个组成环的尺寸信息[10]如下：

Step4：公差分析设计模块的使用。运用蒙特卡罗法对各个尺寸进行模拟抽样分析。

对以上不同抽样次数得到的封闭环尺寸进行统计，以统计次数为纵坐标，以封闭环尺寸区间为横坐标，各个分布图如图6所示。

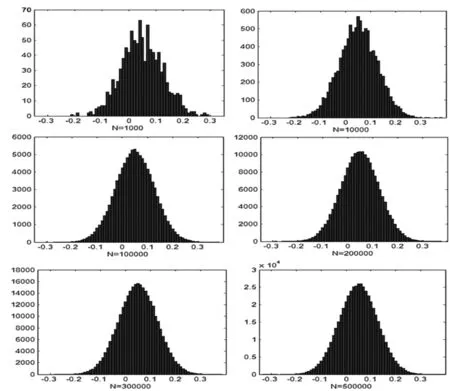
图6 封闭环尺寸分布图

由表1和图6可以看出抽样次数在低于1万时，封闭环公差有显著变化，抽样次数超过1万次时，封闭环公差变化已趋于平缓，抽样次数超过10万次时，封闭环尺寸基本符合统计学中的大数定理和中心极限定理，同时也符合实际的尺寸分布，封闭环的公差基本稳定在0.460左右，因此运用蒙特卡罗法求得的封闭环公差在模拟次数10万以上时可以得到较高的精度。

表1 实验结果

根据以上分析可知运用蒙特卡罗法得到的公差结果0.46小于极值法所得的封闭环公差0.75，因此同等装配精度要求下，运用蒙特卡罗法模拟、分析装配过程，可以降低各零件的实际加工精度。在产品的设计、装配过程中，通过此软件对装配模型进行尺寸链生成、公差分析，可以得到满足装配精度要求的装配尺寸链，并且组成环尺寸精度根据实际加工可以适当放大，降低加了工成本。

4 结束语

本文提出了一种新的面向公差设计的装配信息用户数据结构，优化了尺寸链生成的搜索算法，详细介绍了Creo约束机制中装配约束特征的识别和提取；开发了一套实用的基于装配尺寸链自动生成的公差分析软件，其操作方便、快捷、人机交互性好、集成程度高；为产品设计人员在进行装配设计的时候提供了便利，通过虚拟装配干涉检验，确定装配精度，直接在设计环节进行修改，提高了工作效率;实现公差设计由传统的经验数据到精确的数值分析，提高了设计的准确性和制造水平，节约了制造成本。并结合实例验证了实用性。

[1]王恒,宁汝新. 计算机辅助公差设计与分析的研究现状及展望[J]. 航空制造技术,2006(3):73-75，102.

[2]何景熙,肖迪,王灿.计算机辅助二维装配尺寸链分析计算关键技术研究[J].组合机床与自动化加工技术,2002(4):51-53.

[3]王恒,宁汝新,唐承统. 三维装配尺寸链的自动生成[J]. 机械工程学报,2005,(6):181-187.

[4]王克冲. 用蒙特卡罗法解尺寸链问题[J]. 南京理工大学学报(自然科学版),1985(1):53-59.

[5]刘飞. 基于Pro/E的装配公差设计研究[D].哈尔滨工程大学,2010.

[6]刘之生.尺寸链理论及应用[M].北京：兵器工业出版社，1990(1)：122-124.

[7]杨文龙.面向装配的公差设计系统研究[D]. 哈尔滨：哈尔滨工业大学,2011.

[8]董银月. 基于蒙特卡洛方法和改进PSO算法的装配公差优化设计[D].武汉：华中科技大学,2011.

[9]王兆证. 计算机辅助尺寸公差设计的研究[D].南京：南京农业大学,2002.

[10]赵金才,刘新凯,刘书桂.基于Pro/Toolkit的实体模型尺寸信息的提取[J].组合机床与自动化加工技术,2005(3):22-24.

(编辑 李秀敏)

Development and Application of Computer Aided Tolerance Design

WEI Jian-dong，LI Jing-rong，SU Hang-peng

(School of Mechanical and Automotive Engineering,South China University of Technology , Guangzhou 510641,China)

Based on the current computer aided tolerance design software operation is complex and lack of assembly dimension chain analysis of the status quo, this paper builds data structure for tolerance design of assembly information, to facilitate the analysis of tolerance design; on the basis of the generation assembly dimension chain algorithm of the optimization and used Monte Carlo method to tolerance analysis ,developed a set of application software which based on assembly dimension chain automatic generation of computer aided tolerance design module , in the mainstream 3D modeling software Creo on the secondary development platform to achieve, and an example provided to testify the practicability .

computer-aided tolerance design; assembly dimension chain; creo secondary development;Monte -Carlo

1001-2265(2014)01-0064-04

10.13462/j.cnki.mmtamt.2014.01.018

2013-05-27；

2013-06-30

魏建东(1987—)，男，河南南阳人，华南理工大学硕士研究生，研究方向为数字化设计与制造，(E-mail)wjd1425@163.com；

TH164；TG65

A