对等量异种点电荷电场的研究
2014-07-14胡昌胜
胡昌胜
(枞阳县宏实中学 安徽 安庆 246700)
等量异种点电荷的电场是静电场中的重要内容,也是难点内容.准确全面认识等量异种点电荷的电场,对学好静电场的内容尤为重要.本文通过理论分析辅助多媒体作图确定等量异种点电荷的电场分布情况.下面我们按照从简单到复杂的原则,先从两条线(等量异种点电荷的连线、连线的中垂线)上的电场入手进行分析.
1 等量异种点电荷连线上的电场强度和电势
等量异种点电荷的电场分布图如图1所示,根据电场线的疏密程度,我们知道连线上越靠近中点O场强越小,两侧关于连线中点O对称.
可进行理论证明如下:
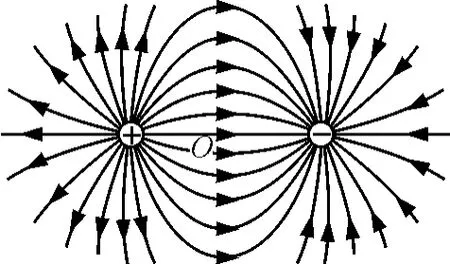
图1
设两点电荷电荷量分别为+Q和-Q,两电荷间的距离为2L,以O为原点,连线为x轴建立直角坐标系如图2所示,我们讨论连线或连线的延长线上P(x,0)点的电场强度.

图2
规定+x方向为电场强度E的正方向,则由点电荷的场强公式及电场的叠加原理知P点的电场强度为[1]
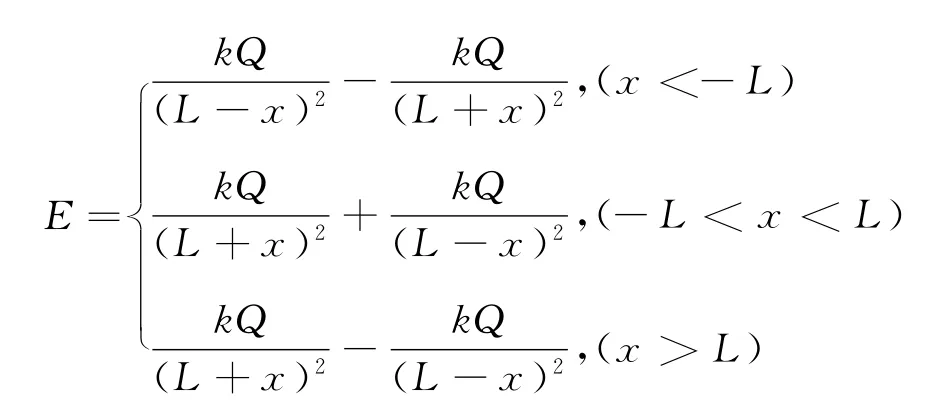
可见E是x的函数,用几何画板作图如图3所示(以从正电荷指向负电荷为电场强度E的正方向).
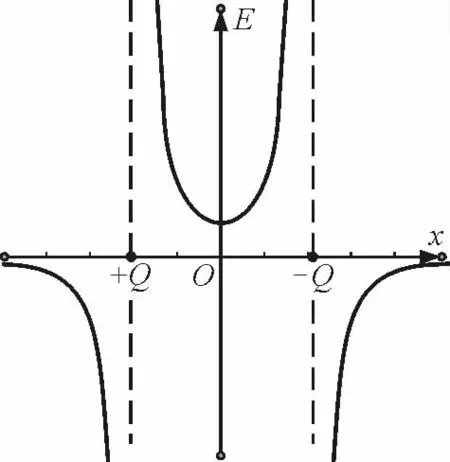
图3
结论1:在等量异种点电荷的连线上,从连线中点沿连线向两电荷移动时,电场强度逐渐增大,在连线的延长线上,离点电荷越远电场强度越小,且二者连线上电场强度大小关于中点O对称,中点位置的电场强度最小,但不为零.
【例1】(2009年高考上海卷第3题)两带电荷量分别为q和-q的点电荷放在x轴上,相距为L,能正确反映两电荷连线上场强大小E与x关系的是图4中的
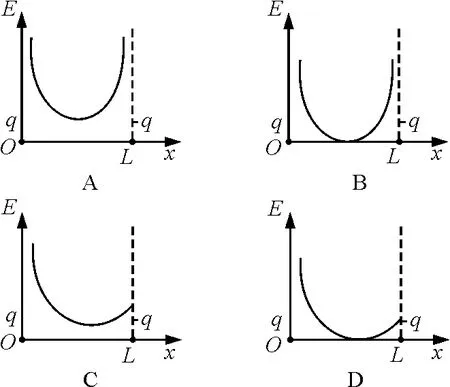
图4
解析:根据等量异种点电荷的电场线的分布情况可知,靠近两点电荷电场强度较大,中点的最小,但不是零,因此正确的选项为A;或直接由图3知正确答案为A.
电势高低变化.
理论推导:规定无限远处电势为零,则由点电荷电场的电势的计算式可得图2中P(x,0)点的电势为[2]
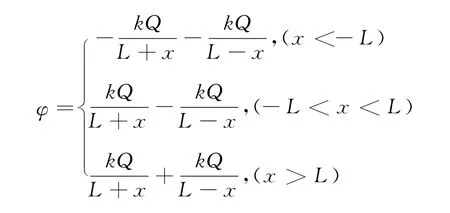
可见φ是x的函数,用几何画板作图如图5所示.
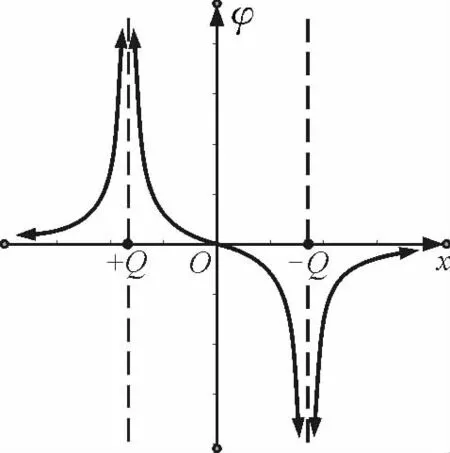
图5
结论2:在等量异种点电荷的连线上,从正电荷向负电荷移动时,电势逐渐降低;连线中点电势为零,靠近正电荷一侧电势大于零,靠近负电荷一侧电势小零.在连线的延长线上,离正点电荷越远电势越低,离负点电荷越远电势越高.
【例2】(2011年高考上海卷第14题)两个等量异种点电荷位于x轴上,相对原点对称分布,正确描述电势φ随位置x变化规律的是图6中的
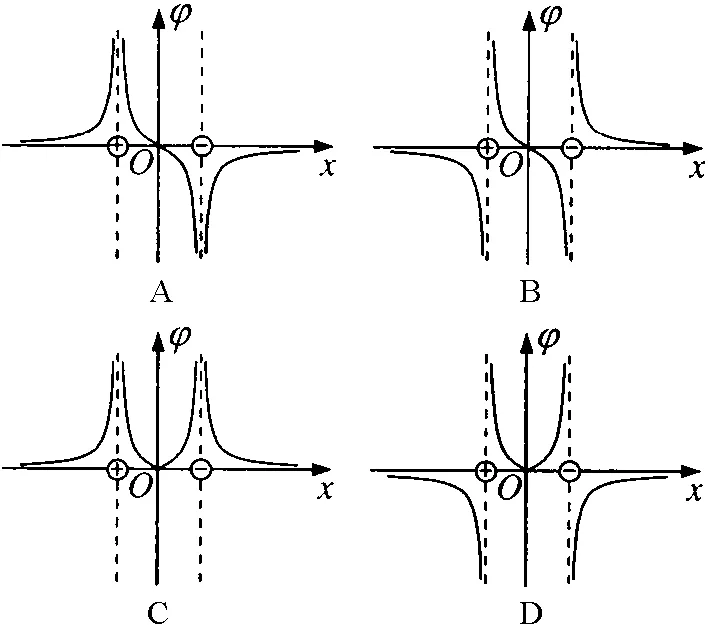
图6
解析:由于沿电场线方向电势降低,所以正电荷处电势最高,负电荷处电势最低.由于两电荷电荷量相等,其连线中点电势为零,故选A;或由图5知,图6中A图正确.
2 等量异种点电荷连线的中垂线(面)上电场强度和电势
以连线中点O为原点,连线为x轴建立直角坐标系如图7所示.设等量异种点电荷连线的中垂线上P点坐标为(0,y),则由点电荷的场强公式得:
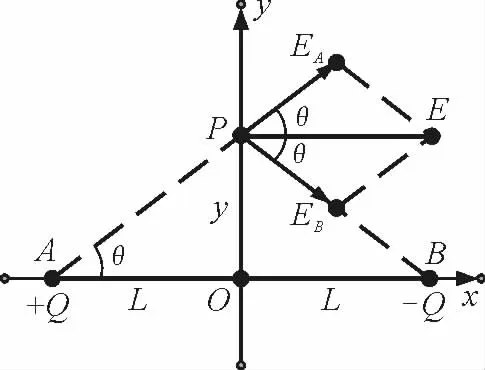
图7
电荷+Q在P点产生的电场强度大小为
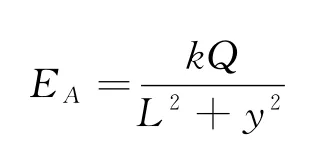
电荷-Q在P点产生的电场强度大小为
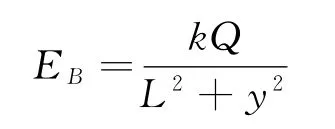
方向与连线的夹角均为θ,则由场的叠加原理得
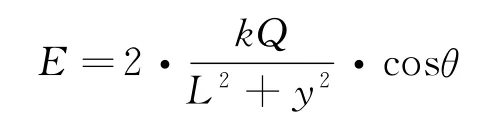
而
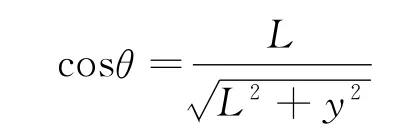
从上式可以看出,当y绝对值增大时,E减小.
几何画板作图如图8所示.
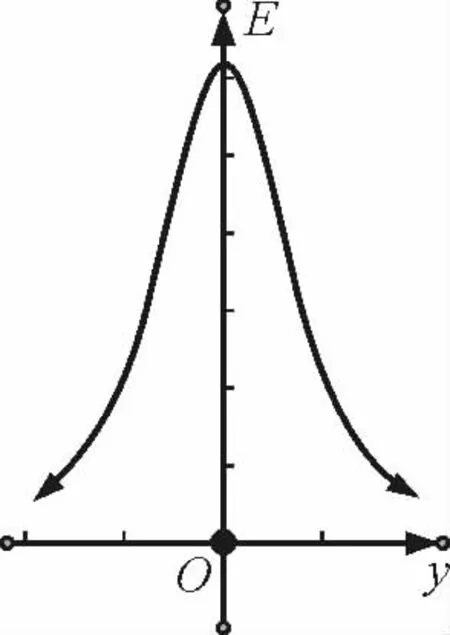
图8
结论3:在等量异种点电荷连线的中垂线(面)上,从垂足沿中垂线(面)向外侧移动时,中垂线(面)上的各点的电场强度减小且中垂线(面)上关于中点O对称的两点场强相同,方向始终垂直于中垂线(面)指向负电荷一侧.
电势高低分析:
若规定无穷远电势为零,则等量异种点电荷连线的中垂线(面)上P(0,y)的电势为
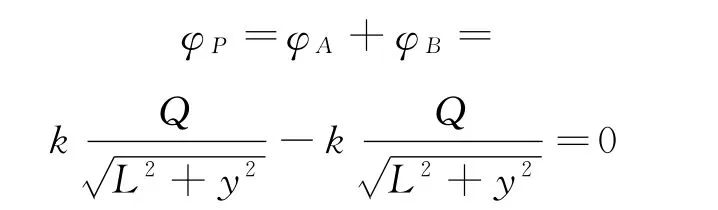
结论4:等量异种点电荷连线的中垂线(面)上任意一点电势均为零,即等量异种点电荷连线的中垂线(面)是零势线(面).
3 等量异种点电荷电场中几类特殊点的电场强度和电势
3.1 关于连线中点对称的任两点的电场强度和电势
理论证明:如图9所示,我们研究等量异种点电荷的电场中关于连线中点O对称的两点M,N的电场强度和电势的关系.两电荷在M,N两点均产生电场,方向如图10所示.因M,N关于O点对称,故可设则根据点电荷的场强公式可知场强大小关系为.又由几何知识可知四边形AMBN为平形四边形,因此EA1与EB2的方向相同,EA2与EB1的方向相同,即两矢量分别相等EA1=EB2,EA2=EB1,合场强也相等.
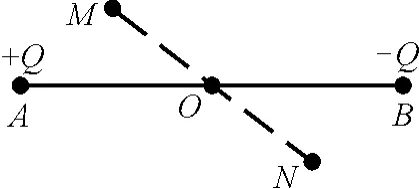
图9
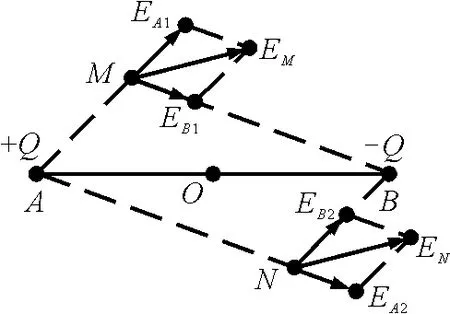
图10
结论5:等量异种点电荷电场中的任两个关于连线中点对称的点的电场强度总相同,以中垂线为界靠近正电荷一侧的各点的电势总高于靠近负电荷一侧的各点电势.
3.2 等量异种点电荷连线的垂线(面)上各点电势
以等量异种点电荷的连线中点O为原点,连线为x轴建立直角坐标系,研究直线x=a(常数)上各点的电势φ随y的变化,即连线的某一垂线(面)内各点电势的变化情况,设点为P(a,y),如图11所示.
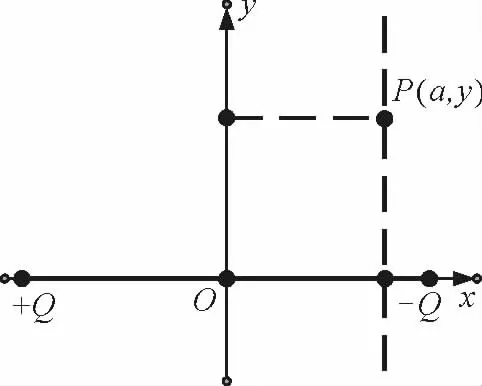
图11
由点电荷电势的计算式及电势的合成得
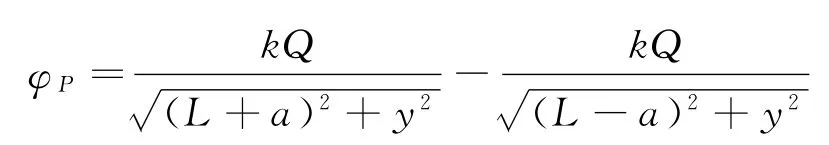
几何画板作图如图12所示.
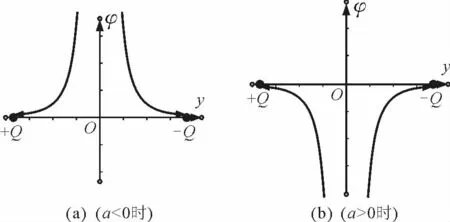
图12
结论6:若连线的垂线(面)在中垂线靠近正电荷一侧,则从垂足沿垂线(面)往外侧电势逐渐降低,如图12(a);若连线的垂线(面)在中垂线靠近负电荷一侧,则从垂足沿垂线(面)往外侧电势逐渐升高,如图12(b),且关于连线对称.如以连线上任一点为圆心在垂直连线的平面内作圆,圆上各点电势相等.
3.3 等量异种点电荷连线的平行线上各点电势
以等量异种点电荷的连线中点O为原点,连线为x轴建立直角坐标系,研究直线y=b(常数)上各点的电势φ随x的变化,即连线的某一平行线上各点电势的变化情况,设点为P(x,b),如图13,则
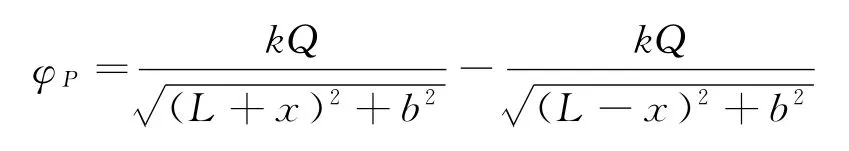
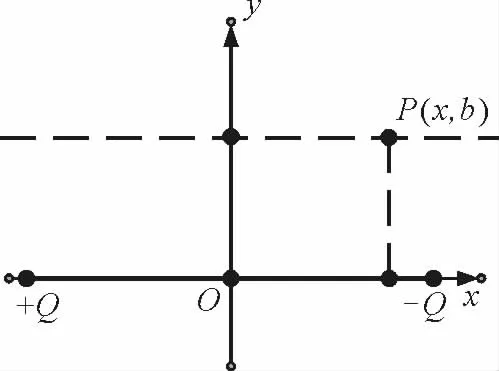
图13
几何画板作图如图14所示.
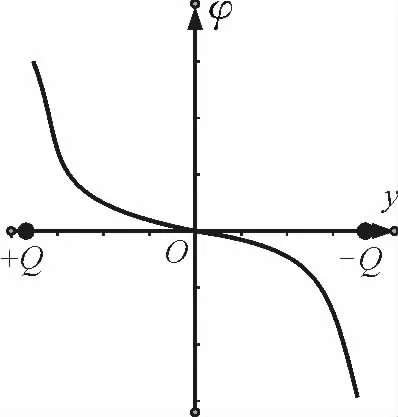
图14
结论7:在等量异种点电荷连线的平行线上,从正电荷一侧指向负电荷一侧电势逐渐降低,且关于中垂线对称的两点电势绝对值相等.
【例3】如图15所示,由ABCD-abcd作为定点构成一正方体空间,在顶点A,c两处放等量异种电点荷,则下列说法正确的是
A.a,C两点场强相同
B.D,b两点间电势相等
C.D,d两点间电势差大于B,b两点间电势差
D.负电荷沿BCD从B点到D点电场力做正功

图15
解析:设正方体的中心为O点,由正方体的空间特点可知,a与C关于O点对称,则由结论5可知答案A正确.D与b也关于O点对称,但D与b分别位于等量异种点电荷垂直平分线的两侧,其中D在靠近正电荷的一侧,由结论5知电势高于b点,故选项B错.
B和D在垂直A与c连线的同一面内且到连线的距离相等,由结论6可知φB=φD;b,d在垂直A,c连线的另一面内,到连线的距离也相等,故φb=φd,得UDd=UBb,所以选项C和D均错.
研究等量异种点电荷的电场时,理论分析辅以几何画板作图,让等量异种点电荷的电场理性但不失感性,抽象不乏形象,将无法感知的电场立体、生动地呈现在我们眼前,同时也提供了数形结合法解决物理问题的绝好范例.
1 梁灿彬,秦光戎,梁竹健.电磁学.北京:高等教育出版社 ,1980.12
2 陈燕.两等量异种点电荷电场的探讨.物理教师,2012(02):21
