探求礼花弹落地点和燃放点间最大水平距离
2014-07-14阙志武
阙志武
(南城县第一中学 江西 抚州 344700)
通过网络搜索,查找到试题来源于《福建省厦门市2013届高三3月质量检查物理能力测试》第20题.参考答案的解释为“爆炸后沿水平方向飞出的小火球落地点距离燃放点水平距离最大”,然后运用平抛运动的规律,求出最大水平距离.有的教师会认为参考答案错了,其实不然,探究之下还颇有一番意味.
1 试题
每年农历正月初一晚上,厦门与金门两地同时燃放礼花,成为两地民众共同庆祝新春佳节的活动.在空旷的水平地面上燃放礼花,使礼花竖直向上发射,当它上升到最大高度H处恰好瞬间爆炸,爆炸产生许多个“小火球”,假设这些“小火球”同时以相同初速度大小v向各个方向运动,如图1所示.

图1 礼花燃放的照片
(设礼花上升和“小火球”运动过程,均只考虑重力作用,重力加速度为g)求:“小火球”的落地点和燃放点间最大水平距离x.
2 求解
对于此题的常规解法有两种,一种是通过消去未知数t,得到x关于θ的方程,然后利用判别式法求解;另外一种是利用矢量图像法,见参考文献[1].此两种方法的弊端是不利于高中生接受.学生熟悉的是一元二次函数求最值.抛出的角度θ和落地时间t相互制约,既然可以消去t,也就可以消去θ.通过求出t来确定θ.

图2
解:如图2所示,以爆炸处为原点,水平向右建立x轴,竖直向下建立y轴.设爆炸时某一小火球的速度方向与水平面成θ角,从爆炸到落地的时间为t,小火球的落地点和燃放点间最大水平距离为x,依题意有

式(1)两边平方、式(2)移项后两边平方得
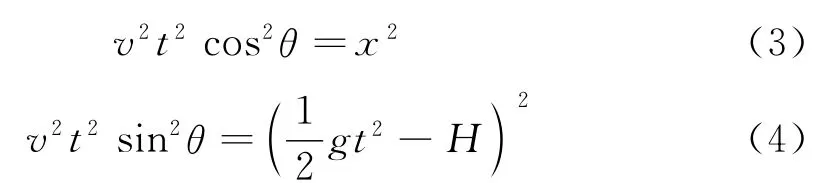
式(3)和式(4)两边相加得

展开、合并同类项得

把t2看成自变量、x2看成因变量,式(6)则看成x2关于t2的一元二次函数,当

x2取得最大值

把式(7)代入式(4)得

因此,落地点和燃放点间最大水平距离

与此对应的抛出角度为

3 评估讨论
(1)当H=0时
结果表明,贴着与地面成45°抛出时的射程最远.
结果表明,出现最大水平距离时,对应的抛出速度与水平面之间的夹角
(3)虽然v与H不是同一类型物理量,不具可比性.但是仅仅比较数值大小,当v2远小于H时

结果表明,当v2远小于H时,爆炸后沿水平方向飞出的小火球落地点距离燃放点水平距离最大.此时,转化为平抛运动.具体验证如下:
以爆炸处为原点,水平向右建立x轴,竖直向下建立y轴.爆炸时小火球水平飞出的速度大小为v,从爆炸到落地的时间为t,小火球的落地点和燃放点间最大水平距离为x,依题意有

联立式(11)、(12)解得

4 反思参考答案
物理教学中,对于实际生活中的问题,可以建立物理模型进行理论研究,突出主要问题,忽略次要因素,但是最终还是需要回到实践检验.此题作为实际问题,理所当然也要回到题目的情境——隔海相望的厦门金门,燃放高空焰火.此情境中高度H较大,可以认为v2远小于H.因此,参考答案近似处理为爆炸后沿水平方向飞出的小火球落地点距离燃放点水平距离最大,即按照平抛运动的规律处理此题,不无道理.
1 舒幼生,钟小平.新编高中物理竞赛培训教材(第一分册).杭州:浙江大学出版社,2010.49~50
