动能定理不能乱用

鄢和清

（中山市小榄中学 广东 中山 528415）

用动能定理处理问题时总是显得方便又快捷，这是广大师生普遍的感觉 .在高中各种版本的物理教材上，动能定理一般都是这样表述的：合外力对物体所做的功等于物体动能的变化.至于这里所指的“物体”是个什么样的物体，一般不做说明，事实上高中阶段也不宜做过多的讨论.正因如此，我们在应用动能定理时，其适用对象一般不给予细致的关注，加之物体内部各种能量的转化不易觉察，极易犯经验上的错误.下面讨论的问题就是一个极好的例证.

【原题】ab是一条柔软、光滑、不可伸长、无弹性的细绳，其长度为L，质量为m，静止在光滑的水平面上.如图1所示，若在a端施加一个水平向右的恒力F，当a端前进2L的距离时，b端刚好被拉动（绳子刚好拉直）.求此时绳子的速度大小v.

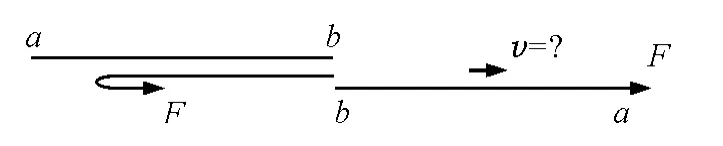
图1

解析：一种解法为人们广泛采用，应用动能定理，只要能求出合外力做的功就行.外力F对绳子做的功为2FL，且没有摩擦力做功，根据动能定理，绳子的动能的增加量等于合外力做的功.即

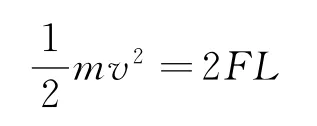
得

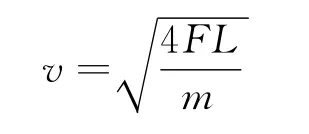
多快捷！一根细绳，仅一个外力做功（没有摩擦），用动能定理来求解当然是首选，相信大家都有同感.可这个解法不正确，因为这里存在一个难以觉察的问题，就是这个过程中绳子有一部分动能损失转化成内能，动能定理在这里不能乱用.

绳子竟然有一部分动能损失？是怎样损失的？为了方便解释，我们先建立一个模型来替代绳子，如图2所示.小球（质点）之间用柔软、轻质、光滑、不可伸长、无弹性的细绳相连，拉动时小球一个带动一个后就立即同速前进，因此这个模型是可靠的.当然我们还是先从高中知识层面来分析它.

图2

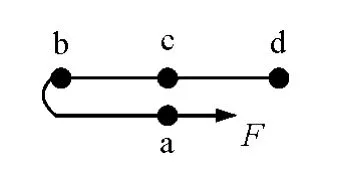
图3

图3是图2中的一部分，a球是第一个被拉动的小球，b为第二个，依此类推.设每个小球的质量为m0，它们之间的细绳长为l.最初，当a球前进了2l时，其速度为v1，由动能定理

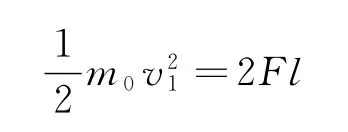
得

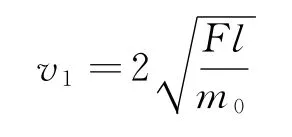
接着b球被拉动，a，b两球立即有共同速度v2，由动量守恒定律

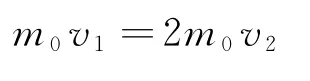
得

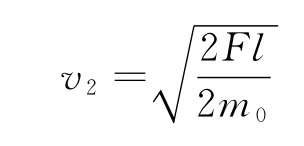
可得出b球被拉动瞬间，系统损失的动能为

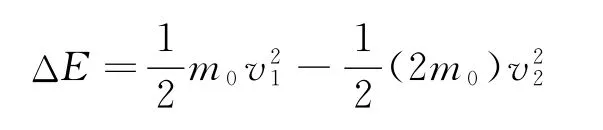
恰好等于Fl.

当a球再前进了2l，a，b两球的速度为v′2，由动能定理

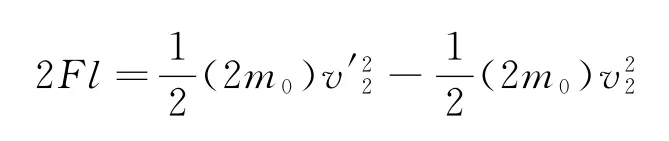
得

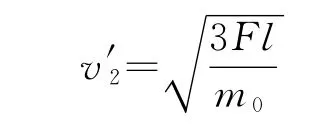
紧接着c球被拉动，三者立即有共同速度v3，由动量守恒定律

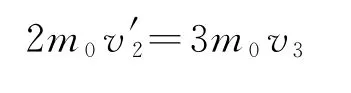
得

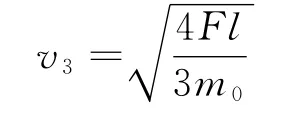
c球被拉动瞬间，系统又损失的动能也为Fl.依此类推，4个小球共同速度为

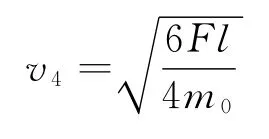
5个小球共同速度

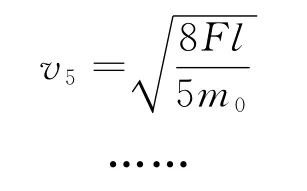
n个小球共同速度

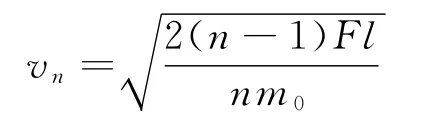
若模型共有n个小球，则总质量m＝nm0，总长度L＝（n－1）l，那么模型刚好拉直时的速度大小

损失的动能为

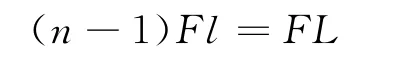
也就是说，细绳刚好拉直时的速度大小为

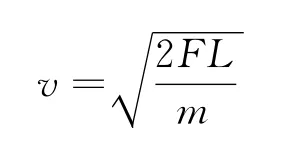
而不是

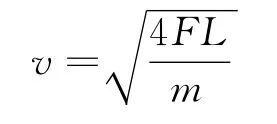
绳子动能的增加量只有

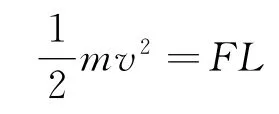
而不是

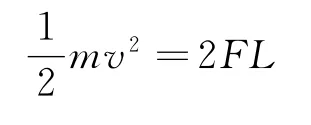
尽管合外力做功为2FL.可见动能确有损失，并转化成为内能.故不可以用动能定理一步到位地求出细绳刚好拉直时的速度大小.

上述论证过程比较繁琐（高中层面只能如此），现用一个更简单的办法进行印证.大学物理中有一条定理叫“质心运动定理”［1］，其内容是“质点组质量与质心的加速度的乘积总是等于质点组所受一切外力的矢量和”.利用质心运动定理，可求得细绳质心的加速度为

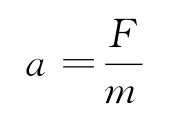
由于细绳刚好拉直时细绳质心的位移恰好为L，应用

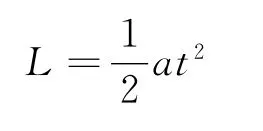
可求出

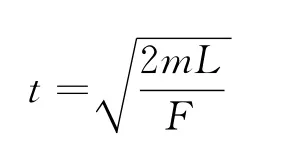
再由v＝at求出质心前进L时的速度

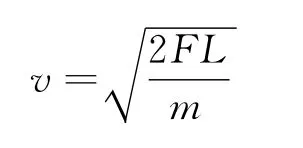
由于拉直时质心的速度与细绳每一点的速度都一样，所以细绳刚好拉直时的速度大小

“应用动能定理也要看适用对象”，中学阶段一般不做强调.大学物理教材对这一点却描述得很详尽，一个是“质点的动能定理”［1］，另一个是“质点组的动能定理”［1］.

质点的动能定理是这样表述的：质点动能的增量等于作用于质点的合力所做的功.高中教材表述的“动能定理”与“质点的动能定理”基本一致，适用对象是质点类物体.在高中阶段研究的对象也大多数是质点类物体.

质点组的动能定理是另样表述的：质点组动能的增量在数值上等于一切外力所做功与一切内力所做功的代数和.

上面讨论的细绳只能是看成质点组，既有外力做功（外力F对绳子做的功为2FL），也有内力做功（绳子内一个质点拉动下一个质点时，内力做负功，经分析可以求出细绳内力所做的负功为－FL）.如果已知内力所做的功，那也可用质点组的动能定理一步到位地求出细绳刚好拉直时的速度大小.高中阶段显然不涉及此类问题.

有些质点组类的物体在运动中内力做功为零，那按照质点组的动能定理，只需考虑外力做的功，高中阶段也涉及过这类物体.

比如图4中一根光滑的链条从光滑的桌面边缘滑下，求链条离开桌面时的速度大小.这时链条在运动中虽不能看成质点，只能是质点组，但内力做功为零，只需考虑重力做功.

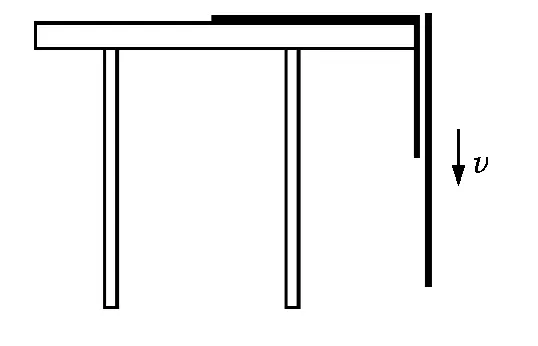
图4

综合以上分析，可以得出这样的体会，高中阶段进行动能定理的教学时，虽然定理对适用对象不作说明，但教师要心中有谱，像上述细绳这样有内力做功的质点组类物体就不要涉及，以免出现上述胡乱应用的错误或加重教学负担.

1 漆安慎，杜婵英.力学基础.北京：高等教育出版社，1982.157，198