非匀强场中感应电动势的计算

赵永生

（九江县第一中学 江西 九江 332100）

2013年高考上海物理试卷第33题是一道有关法拉第电磁感应定律应用的题，题目如下：

【原题】如图1，两根相距L＝0.4m，电阻不计的平行光滑金属导轨水平放置，一端与阻值R＝0.15Ω的电阻相连.导轨x＞0一侧存在沿x方向均匀增大的稳恒磁场，其方向与导轨平面垂直，变化率k＝0.5T／m，x＝0处磁场的磁感应强度B0＝0.5T.一根质量m＝0.1kg，电阻r＝0.05Ω的金属棒置于导轨上，并与导轨垂直.棒在外力作用下从x＝0处以初速度v0＝2m／s沿导轨向右运动，运动过程中电阻上消耗的功率不变.求：

（1）回路中的电流；

（2）金属棒在x＝2m处的速度；

（3）、（4）略.

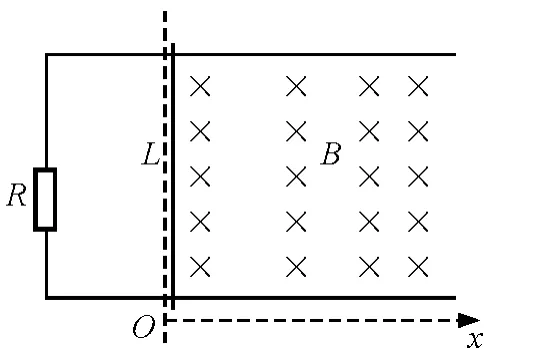
图1

题中涉及非匀强稳恒磁场中直导体切割磁感线产生感应电动势的计算，解法如下.

解法1：用平均值思想

由于磁感应强度沿x方向均匀增加，所以运动到x处回路中的磁通量

运动到x处Δt（Δt→0，Δt内的位移为Δx）时间内回路中磁通量的变化量

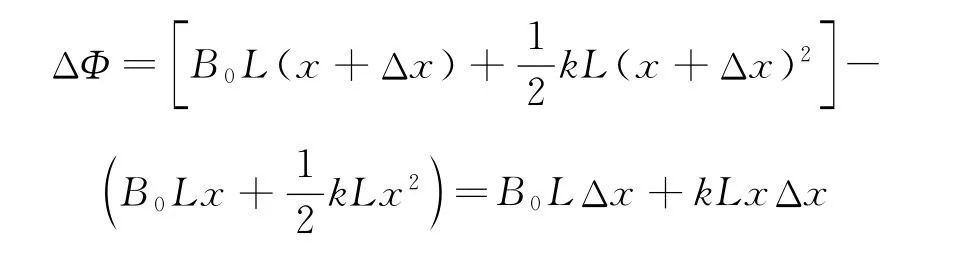
由法拉第电磁感应定律

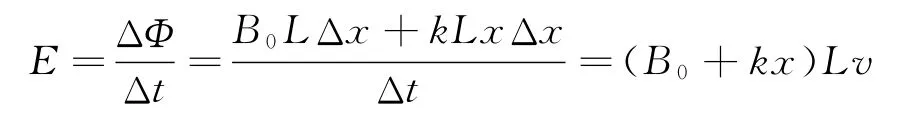
解法2：用微积分方法

由于磁感应强度沿x方向均匀增加，所以运动到x处回路中的磁通量

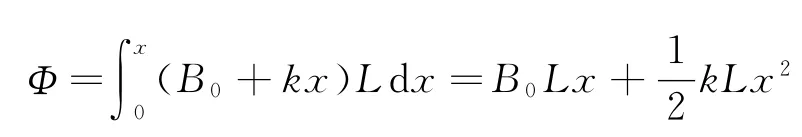
由法拉第电磁感应定律

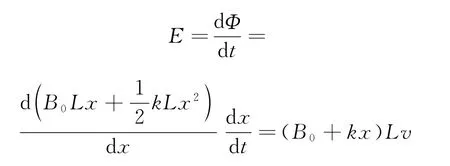
解法3：用直导体切割磁感线产生感应电动势推论

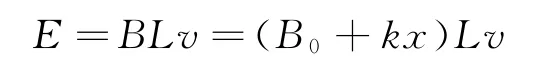
小结：三种解法比较而言，直接应用直导体切割磁感线产生感应电动势推论计算最为简捷.

1 陈鹏万.电磁学（第1版）.北京：人民教育出版社，1978

2 樊映川.高等数学讲义上册（第2版）.北京：人民教育出版社，1964