含落角约束打击运动目标滑模制导律设计

王荣刚

（西北工业大学 航天学院，陕西 西安 710072）

含落角约束打击运动目标滑模制导律设计

王荣刚

（西北工业大学 航天学院，陕西 西安 710072）

以打击地面运动目标为研究对象，提出了一种带落角约束的滑模变结构制导律。通过将目标视为参照原点，从而将定常速度打击运动目标的问题转化为时变速度打击固定目标的问题。在此模型基础上，进一步分析得到了打击运动目标的稳定状态条件。结合该稳定状态及落角约束条件，利用滑模变结构理论设计得到该制导律。仿真结果表明，该制导律可以对运动目标实现全向打击并且具有良好的制导性能。

落角约束；运动目标；滑模变结构制导律；稳定状态

导弹命中目标时，不仅希望获得最小脱靶量，往往还希望命中目标时姿态最佳，使战斗部发挥最大效能，取得最佳毁伤效果[1-7]。如希望反坦克导弹能够以接近垂直下落的方式命中目标的顶装甲以获得最大穿深。文献[3]提出了一种基于偏置比例导引法的带落角约束打击地面运动目标的制导律。该制导方案扩大了导弹的捕获域。然而，当采用该制导方案以尾追方式攻击目标时，导弹的制导性能会下降。通过调整比例导引法中导引系数的值，文献[4]提出了一种可以实现全向打击地面固定目标的两阶段比例导引法。文献[5]进而又将该制导方案扩展到全向打击地面运动目标的情况。然而，这两种制导方案均需要改变制导模式。由于可能会造成控制系统的不稳定，因而制导指令的突然改变是不可取的。

另一方面，公开文献里发表有众多的针对地面静止目标的制导律。文献[6]提出了一种间接作用角控制的偏置比例制导律。文献[7]通过引入偏差反馈来获得了一种基于比例导引法的拦截角控制制导律。因而，如果能建立起打击静止目标与运动目标之间的转化关系，则大量的针对静止目标的制导算法便可通过适当的改进来让其实现对运动目标的打击。

为了解决这些问题，通过对弹目相对运动关系进行研究，本文建立起打击运动目标与打击静止目标两类问题之间的转化关系，从而可将常值速度打击地面运动目标的问题转化为时变速度打击固定目标问题。基于以上的简化处理，通过分析得到了适用于打击运动目标的弹道特性以及制导参数条件。在此基础上，结合实际的角度约束条件，利用滑模变结构方法，可解决该含落角约束打击运动目标的问题。

1 模型的建立

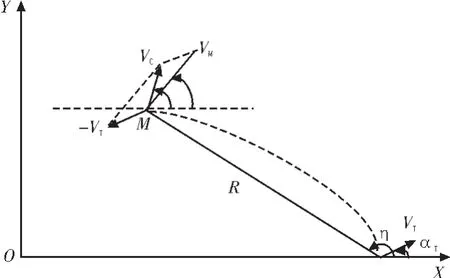
图1 拦截几何关系Fig. 1 Engagement geometry

导弹与目标的拦截几何关系如图1所示，其中XOY为惯性坐标系，VM和VT分别为导弹和目标的速度向量。本文假设VM和VT均为常值速度。导弹与目标的运动方程为

式中：αM为导弹的飞行轨迹角；αM为导弹的法向加速度；αT为目标的运动轨迹角；η为视线角。导弹与目标的相对速度矢量用VC表示，其为导弹速度矢量与目标速度矢量的合成，即

定义ψ为相对飞行轨迹角，其为相对速度矢量与基准线之间的夹角(逆时针为正)，如图1所示。通过投影关系可知，相对速度的大小为

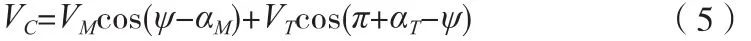
虽然假设导弹速度与目标速度大小为常值，但由式(5)可知，通过转化后，由于ψ和αM为时变的，因而相对速度VC也是时变的。同样，相对飞行轨迹角的值可以通过下式获得

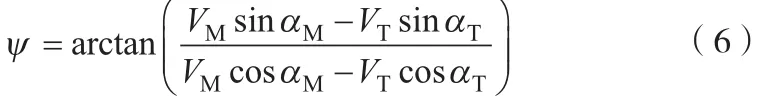
由式(6)可知，当目标静止时，ψ=αM。因而，打击静止目标的问题只是打击运动目标的一类特殊情况。对式(7)两边求导，可得

当目标在平地、坡度起伏不大的路上或者海面上运动时，αT的变化率基本为零，上式可简化为

根据式(8)，飞行轨迹角速率可由下式给出

式(9)右边的系数实质上建立了针对地面静止与运动目标问题之间的转化关系。因而，假设整个过程理想跟踪，便可以通过对相对飞行轨迹角指令进行设计而间接获得飞行轨迹角指令。而对相对飞行轨迹角指令的设计过程实际对应的是解决一个时变速度打击静止目标的问题。基于以上转化和处理，式(1)和式(2)可以简化为

以上两式与打击静止目标时的运动方程类似，唯一不同在于，此处用的是相对飞行轨迹角，而打击静止目标时用的是飞行轨迹角。

文献[8]分析了利用比例导引法打击地面固定目标时的制导参数条件以及弹道特性。据此，需要将该方法进一步推广到打击运动目标时的情况。由以上分析可知，相对飞行轨迹角速率与飞行轨迹角速率成比例。依据比例导引法的思想，飞行轨迹角速率又与视线角速率成比例。因而，相对飞行轨迹角速率与视线角速率也成比例，即

式中：NC为相对比例系数。此处，为了便于分析NC取不同值时对弹道特性的影响，在此假设其为常值。定义Φ=η-ψ，并结合式 (10) (11)和 (12)可得

对上式进行积分可得

结合式(14)和式(15)，分析后可得到以下结论：

1)导弹命中目标的必要条件为NC＞1，该条件可保证导弹在命中目标时R→0。

2)当2＞NC＞1时，当导弹接近目标时R→0，Φ→π，但视线角速率会趋近于一个很大的值。说明在此情况下，导弹在击中目标时，法向加速度会很大。

3)当NC＞2时，当导弹接近目标时R→0，Φ→π，视线角速率也会趋近于零。说明在此情况下，导弹在击中目标时，法向加速度会收敛到零附近。

4)当NC＞1时，由于式(14)和式(15)的值会发散，说明在此条件下导弹无法击中目标。

由以上特性可知，当导弹击中目标时，总有Φ→π，即

式中：ηf为终端视线角；ψf为终端相对飞行轨迹角。该情况对应的物理现象为相对速度向量指向目标的状态。

2 基于滑模变结构制导律设计

对式(11)两边对时间 进行求导，可得到

根据终端约束的要求，目标线角速率必须收敛至零，同时末端视线角要同时满足角度约束以及终端稳定状态条件，从而可以得到

式中：tf为终端时刻。αM为约束角，其终端值为αMf，则ψf可以通过下式进行计算

对此，根据式(16)的结论，选取如下量作为状态变量：

由上式得到了针对运动目标的状态方程。另外，制导律要同时满足零脱靶量和末端落角约束角要求，故选取滑模面的切换函数为

结合文献[9]的趋近律形式，选取滑模面的趋近律为

对式(22)两边进行求导，并与式(23)对比，并定义角误差项εr=η-ψf-π ，经整理不难得到相对飞行轨迹角速率指令为

将式(24)代入式(9)，可得

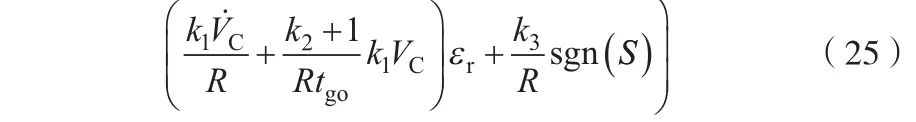
式(25)即为所提出的打击运动目标的滑模变结构制导律。

3 仿真结果

文中以地地导弹打击运动目标为例验证本文提出制导律性能。导弹的初始位置的坐标为(xM0,yM0)=(0,0)，目标的初始位置坐标为(xT0,yT0)=(5 000 m,0)，其中，导弹速度VM=300 m/s，导弹初始飞行轨迹角αM0=45 deg，目标VT=50 m/s并沿X轴正方向运动。另外，各制导参数取为K1=2，K2=0.8，K3=0.01 。

图2为本文所提出的制导律（slide-mode guidance,SMG）与文献[5]中的两阶段制导律（Two-Stage Proportional Navigation Guidance, TSPNG）在设置αMf=-90o时的比较结果。图2(a)和图2(b)分别为两种制导律飞行轨迹以及制导指令的比较结果曲线。由图2(a)看出，在进行垂直打击时，本文所提出的制导律比文献[5]中的制导律需要更少的空间来进行机动。另外，通过图2b可以看出，本文所提出的制导律在整个制导过程中产生连续的指令信号，而文献[5]中的制导律由于要进行制导模式切换，制导指令是不连续的。

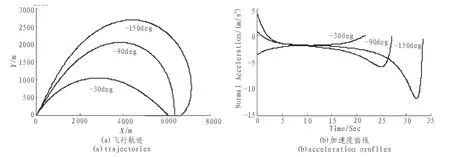
图3 不同角度约束时的性能结果Fig. 3 Performance results for various desired impact angles

图3为采用本文所提出制导律在 deg时的仿真结果。由图3(a)可以看出，在不同落角约束情况下，导弹均能成功命中目标，从而验证了本文所提出的制导律具有全向打击能力。由图3(b)可以看出，在进行小角度约束时，导弹的初始加速度比较小，而进行大角度落角约束时，导弹的初始加速度比较大。另一方面，当落角约束比较大时，在导弹接近目标时，导弹的加速度幅值越大，但最终都收敛到0附近。

4 结 论

针对含落角约束打击地面运动目标这一问题，提出了一种滑模变结构制导律。文中所提出的转化关系可以将常值速度打击运动目标的问题转化为时变速度打击静止目标的问题，利用该方法依然可对其它打击静止目标的制导算法进行适当的改进而使其具备打击运动目标的能力。另外，该制导方案能够产生连续的指令信号，具有很高的落角精度，法向加速度均能收敛到一个较小值，具有良好的收敛性，而且对地面运动目标具有全向打击能力。

[1]Kim M,V K.Grider.Termainal guidance for impact attitude angle costrained flight trajetories[J].IEEE Transactions on Aerospace and Electronic Systems,1973.9(6):852-859.

[2]Lu P, Doman D B, Schierman J D. Adaptive Terminal Guidance for Hypervelocity Impact in Specified Direction[J]. Journal of Guidance, Control, and Dynamics,2006,29(2):269-278.

[3]Kim B S,Lee J G,Han H. S. Biased PNG law for impact with angular constraint[J].IEEE Trans. Aerosp.Electron.Syst,1998,34(1):277-288

[4]Ratnoo A,Ghose D.Impact Angle Constrained Interception of Stationary Targets[J].Journal of Guidance,Control,and Dynamics,2008, 31(6):1816-1821.

[5]Ratnoo A,Ghose D. Impact Angle Constrained Interception of Nonstaionary Nonmaneuvering Targets[J].Journal of Guidance,Control,and Dynamics, 2010, 33(1):269-275.

[6]Erer K S, Merttopcuoglu O. Indirect Impact-Angle-Control Against Stationary Targets Using Biased Pure Proportional Navigation[J].Journal of Guidance,Control,and Dynamics,2012,35(2):700-703.

[7]Lee C H, Kim T H, Tahk M J. Interception Angle Control Guidance Using Proportional Navigation with Error Feedback[J]. Journal of Guidance, Control, and Dynamics, 2013,36 (5):1556-1561.

[8]Lu P.Intercept of Nonmoving Targets at Arbitrary Time-Varying Velocity[J].Journal of Guidance,Control,and Dynamics,1998,21(1): 176-178.

[9]蔡洪,胡正东,曹渊. 具有终端角度约束的导引律综述[J].宇航学报,2010,31(2):315-323.

CAI Hong,HU Zheng-dong,CAO Yuan. A survey of guidance law with terminal impact angle constraints[J].Journal of Astronautics,2010,31(2):315-323.

Impact angle constrained guidance against moving target using slide-mode guidance law

WANG Rong-gang
（School of Astronautics,Northwestern Polytechnical University,Xi'an710072,China）

In this paper, a new impact-angle-constrained slide-mode guidance law against moving targets is proposed.Viewing the target as a reference, we can convert the problem against moving target to the one against stationary target.Then, the new steady-state condition can be obtained by analyzing. Combining the steady-state condition and the impact-angle constraint, the new slide-mode guidance law can be derived. Simulation shows that the guidance law can achieve all impact angles and has a good guidance performance.

impact angle constraint; moving target; slide-mode guidance law; steady state

TN919.6

A

1674-6236(2014)07-0050-04

2014-02-25稿件编号201402173

国家863高新技术研究发展项目(2013AA7022014)

王荣刚(1986—)，男，陕西西安人，硕士研究生。研究方向：飞行动力学与控制。