考虑碳排放的快递企业配送路径研究

代楚楚，徐 菱

（西南交通大学 交通运输与物流学院，四川 成都 610031）

0 引言

快递业作为城市内物流配送业的重要组成部分，其营业额年均增速高达 25%～30%。据测算，我国快递市场规模与 GDP 的增长关系密切，GDP每增长 1%，快递市场规模将增长 2.93%[1]。特别是在电子商务的刺激下，快递业规模将进一步扩大。根据中国电子商务研究中心的监测数据显示：仅2013 年上半年，中国网络购物用户规模达到 2.77 亿人，占中国网民的 40.9%，网络零售市场交易规模达到7 542 亿元[2]，每天由电子商务产生的快件已经超过500 万件。如此巨大数额的快件量配送势必导致碳排放量的大幅提高，因而对快递企业配送路径选择进行节能减排优化将对抑制温室气体排放具有较大促进作用。

在传统的车辆路径问题 ( Vehicle Routing Problem，VRP ) 中，通常将车辆数最少和路径最短作为模型的目标函数，既有研究成果较少将降低碳排放作为一个目标在 VRP 模型中进行考虑。Figliozzi在基于有时间窗约束的车辆路径问题 ( Vehicle Routing Problem with Time Windows，VRPTW ) 中构建考虑碳排放的车辆路径模型 ( Vehicle Routing Problem for Emission Minimization，EVRP )，首次将降低碳排放和减少车辆能耗作为 VRP 问题的目标，第一次将客户服务开始时间作为 1 个决策变量考虑进有时间窗约束的 VRP 问题中，并且考虑不同拥堵条件对车辆碳排放的影响，最后设计路径构造算法 ( Iterated Route Construction and Improvement，IRCI ) 对模型进行求解[3-4]。Saberi 等[5]认为客户点连续均匀分布，存在密度函数，并且任意 2 个客户点间的距离与分布密度有关，因而将速度处理成随旅行时间连续变化的函数，应用连续近似分析模型对问题进行求解。杨子岳[6]研究考虑碳排放的 B2C电子商务企业配送路径优化，通过道路条件、天气状况等参数将电商实际配送路径转化为考虑碳排放的虚拟路径，以此处理速度对车辆碳排放的影响，并且通过禁忌搜索算法对模型进行求解。

由于车辆在行驶过程中的碳排放与行驶距离、行驶速度 2 个变量有关，如果仅在传统的静态车辆路径问题 ( Static Vehicle Routing Problem，SVRP ) 目标函数中加入碳排放最少这一目标并不符合实际。为此，参考 Figliozzi 所建模型，在考虑旅行速度时间依赖性的同时将车辆数最少、旅行时间最短及碳排放最少作为模型的 3 个目标函数，建立基于时间依赖车辆路径模型 ( Time Dependent Vehicle Routing Problem，TDVRP ) 模型的 EVRP 模型，并且设计多种群遗传算法求解模型，为快递企业选择低碳配送路径提供理论支撑。

1 快递企业配送EVRP模型建立

1.1 问题描述

快递企业配送 EVRP 模型基于 TDVRP 模型构建，具有旅行时间严格依赖于出发时间的特点。TDVRP 模型最早由 Malandraki 和 Daskin 在 1992 年提出，问题描述为有n个客户点，每个客户点的需求量及位置已知，至多用K辆车从配送中心出发去服务这批客户点，要求车辆在规定时间内完成任务并返回配送中心，每辆车载质量一定，要求安排车辆的行驶线路使总旅行时间最短。其中，每个客户点的服务时间窗已知，任意 2 个客户点间的旅行时间与距离、出发时间有关[7]。

考虑到快递企业的特殊性，EVRP 模型所描述的问题还需要满足以下条件：①配送与揽收独立进行。在快递企业 1 台车服务 1 个网点的情况下，为避免大量的资源浪费和成本劣势，将配送和揽收同步进行，但国内的快递企业可以达到上述规模的很少，考虑操作的方便性，简化操作流程，节省时间，默认快递企业的配送和揽收独立进行。②每条线路上的客户需求不超过车辆的最大载质量。③每条配送线的距离不超过车辆的 1 次行驶最大距离。④每个客户点有且只有 1 辆车服务。

1.2 模型建立

TDVRP 模型描述与 VRP 模型基本相同，只是在时间段的划分及车辆出发时间的定义上有所不同。TDVRP 模型描述如下。

在 1 个无向图G= (V，A) 上，V= {v0，v1，…，vn} 为顶点集合，A= {(vi，vj) :i≠j∧i，j∈V} 为弧集合。顶点v0为配送中心，停放着K辆型号相同、载质量为Q的车；顶点集合C= {v1，…，vn} 为需要服务的客户集，V中每个顶点都有1 个相应的非负需求量qi≤Q与之对应，服务时间gi≥0。其中，g0= 0，q0= 0。每个顶点允许服务的时间窗为 [ei，li]；车辆到达客户i(i∈C) 的时间定义为ai，服务开始时间定义为si，离开时间定义为bi；对于任意弧 (vi，vj)，对称的距离矩阵dij≥0，旅行时间tij(bi)≥0。假设每辆车的固定成本为C，系统规划时间被分成M段，记为T=T1，T2，…，TM。

在 TDVRP 模型中，旅行时间为出发时间函数，为方便区分，用fij(t) 表示车辆在时刻t出发，从节点i经过 (i，j) 到达j的旅行时间，建立模型如下。

其中：⑵式为每个客户点有且只有 1 辆车到达和服务；⑶式为离开每个客户点的车辆有且只有 1辆；⑷式为每辆车均从车场出发；⑸式为抵达客户的车同时也是离开客户的车；⑹式为每辆车最后回到车场；⑺式为车容量约束；⑻、⑼式为时间窗约束，具体含义为假如 1 辆车从客户i到客户j，那么其在客户j开始服务的时间不能早于到达时间si+ti+fij(si+ti)，同时在j的服务时间窗[aj，bj] 内；⑽式为硬时间窗约束，表示车辆在任意客户点服务完成时间必须在该客户点的服务时间窗内；⑾式为车辆数约束。

1.3 碳排放最小化模型

英国交通运输研究实验室研究表明，车辆在行驶过程中的碳排放与行驶速度、行驶距离 2 个因素有关，并且存在以下关系[4]。

其中，英国交通运输研究实验室经过大量实验模拟出的 3 者关系参数 { ∂0，∂1，∂2，∂3} ={ 1 576，-17.6，0.001 17，36 067 }。在 TDVRP 模型中，每个时间段都有相应的即时速度sm≥0，对于任意i，j，均有发生在时间段T m，表示离开客户i的速度；发生在时间段表示到达客户j的速度，1≤m≤m+p≤M。为相应的距离与时间，满足以下条件。

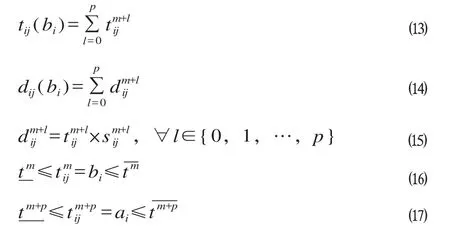
其中：⒀式为客户i，j之间的旅行时间为分段之和；⒁式为客户i，j之间的距离为分段之和；⒂式为车辆在某段时间的行驶距离为对应时间段的速度与时间的乘积；⒃式为时间窗约束，表示将时间段划分，则每个客户点的到达时间和离开时间必在其所属时间段范围内。

任意客户i，j之间的碳排放模型计算公式为

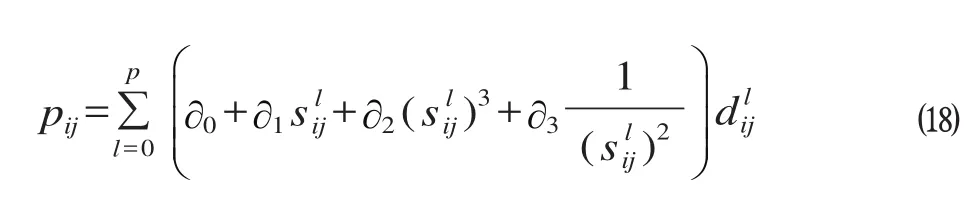
从⒅式可知，任意两点间的碳排放为车辆在不同时间段行驶时碳排放的和。

为对快递企业碳排放进行预防监督，采用碳税换算将快递企业的碳排放成本化。假设碳税税率为w，则碳排放成本模型计算公式为

1.4 模型求解

快递企业配送 EVRP 模型与一般 VRP 模型的不同之处在于：①旅行时间的时间依赖性；②将降低碳排放成本作为目标函数之一。通过调研可知，快递企业通常将 1 次配送的持续时间作为衡量企业 1次配送作业完成的优劣，考虑将配送车辆 1 次配送的旅行时间近似为快递企业 1 次配送的可变成本。因此，模型目标函数为旅行时间、车辆固定费用和碳排放费用之和。快递企业 EVRP 模型的目标函数和约束条件如下。约束条件同⑵式至⑾式，这里不再赘述。

2 模型的求解

（1）染色体编码设计。VRP 问题与旅行商问题 ( Travelling Salesman Problem，TSP ) 一样，适合采用自然数编码的方式来构造染色体[8]。在编码中，数字“0”为配送中心，数字 1，2，…，N为N个客户点，形成的客户点序列首尾均为 0，表示车辆从配送中心出发最后又返回配送中心，其余的“0”插入到客户点序列中，形成诸如 0，1，2，0，3，4，5，0，6，0，7，8，9，0 的序列，表示 4 辆车遍历 9 个客户点形成的 4 条路径：0-1-2-0，0-3-4-5-0，0-6-0 及 0-7-8-9-0。

（2）生成初始解。采用节约法、贪心算法和随机产生初始解的方式生成 3 个初始解，以初始化3 个种群。其中，节约法的流程描述为首先将n个客户点初始成n条独立的路线，每条路线上的 1 辆车服务完当前客户即返回配送中心，形成路径 ( 0，i，0 )；在不违反车容量限制的条件下合并 2 条独立路线，合并方法为“首尾相连”，合并条件为路径节约值最大，这样每次合并即可减少 1 辆车。例如，路线 1 的最后 1 个客户为i，路线 2 的第 1 个客户为j，则合并路线 1 和路线 2 的方式为将弧 (i，0 ) 和弧 ( 0，j)移除，同时添加弧 (i，j)，不断重复上述步骤直到某辆车的车容量不再满足为止[8]。某 2 条路线的路径节约值计算公式为

对贪心算法的流程进行描述：从配送中心 0 开始，从未服务的客户中选择 1 群不违反车容量约束的客户，再在其中挑选 1 个旅行时间最小的添加到已有路线中，同时不能违反该客户点的时间窗；如果从未服务的客户中找不到满足车容量约束的客户，那么该辆车返回配送中心，即 1 条新路径生成。重复上述步骤，直到所有客户均有车辆经过。

（3）种群初始化。每个种群由 1 个初始解通过随机互换算子得到，随机互换算子随机互换路径中2 个客户点的位置，每个子种群分别由 1 个初始解通过随机互换产生。

（4）适应度评价。评价前应先形成可评价的染色体，具体操作为在随机产生的客户点序列中插入车辆“0”，插入准则为车容量约束，直至找出不满足容量约束条件的客户在其前插入“0”，以此形成 1 个可评价解。

（5）选择算子。将所有的个体进行交叉变异，并且按照其适应度值大小进行排序，取一定数量的优秀子代进入新群体。

（6）交叉算子。个体的交叉策略采用 OX 顺序交叉，具体操作方法：随机在父代个体中产生 2 个交叉点 ( 交叉点相同 )，中间部分为交叉区域，把 1个父代染色体的交叉区域部分放置于另 1 父代染色体的交叉区域中，后者检查交叉区域后的部分依次删除与交叉区域中相同的数字，得到 1 条子代染色体，另 1 父代染色体进行同样操作得到另 1 条子代染色体。

（7）变异算子。采用随机互换、随机插入和随机逆转 3 个变异算子，分别用于 3 个种群的变异操作。随机互换算子如图 1 所示，随机插入示意图如图 2 所示，随机逆转算子示意图如图 3 所示。

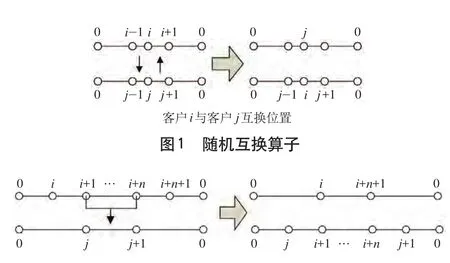
图2 随机插入示意图

图3 逆转算子示意图

（8）移民算子。在多种群遗传算法(Multiple Population Generation Algorithm，MPGA)中，移民算子将各种群在遗传迭代中产生的最优个体间隔固定代数迁移至另外的种群中，从而实现彼此的基因交换。

（9）产生精华种群。在负责遗传操作群进化过程中，每隔一定的代数将最优个体存储到精华种群中，该操作通过人工选择算子实现。

（10）算法终止条件。通过采用精华种群中的最优个体最少保持代数作为算法的停止依据[9]。

3 算例分析

3.1 算例描述

以成都市某快递企业为例，其有 1 个大型配送中心，位于成都市边缘地区，设其坐标为 [5，10]。企业在成都市共有 50 个网点，配送车辆每天在配送中心和网点之间进行 5 次配送作业，配送时间段分别为 ( 6 : 30，9 : 30 )、( 9 : 30，12 : 30 )、( 12 : 30，15 : 30 )、( 15 : 30，18 : 30 ) 及 ( 18 : 30，21 : 30 )，其中第1次配送持续时间段 ( 6 : 30，9 : 30 ) 和第 4 次配送持续时间段 ( 15 : 30，18 : 30 ) 与城市路网的早高峰和晚高峰时段有重叠。由于所建模型的旅行速度考虑到城市路网交通拥堵影响，以每天第 1 次配送为例进行算例分析。在调研中发现，快递企业各网点的服务时间窗均为 1 次配送的持续时间，配送中心与客户网点的工作时间均为 1 次配送持续时间段( 6 : 30，9 : 30 )，配送车辆在每个客户点的服务时间为 10 min。将配送车辆数的上限设为 50，即在最坏的情况下 1 个网点配备 1 辆车，配送车辆型号统一，1 辆车的 1 次投入成本为 1 000。碳排放成本采用碳税制为 10 元。

（1）客户坐标。通过查阅资料，成都市辖区面积为 1 412 km2，将客户坐标限制在边长为 40 的矩形中，通过随机生成产生。客户坐标信息如表 1所示。

（2）客户需求。通过调研可知，该快递企业在配送过程中，每辆车容量平均可以满足 3～5 个客户网点的需求。因此，每次等概率地从集合{ 10，12，15，20，25 } 中随机选取 1 个数作为某个客户点的需求量，并将配送车辆的容量上限设为50。各网点需求量如表 1 所示。

（3）服务时间。快递企业的车辆在各网点不存在服务等待时间，故ai=si，车辆每次配送时间约为 10 min。将算例中客户网点的服务时间定为 11 min，其中 1 min 表示配送车辆在起步和减速过程中浪费的时间。

（4）时间窗限制。由于模型研究对象为快递企业早高峰配送，因而各客户的服务时间窗均为系统规划的 3 h，即 ( 6 : 30，9 : 30 )。

（5）时间依赖旅行速度。以快递企业早高峰配送为例，将早高峰 3 h 分为 6 : 30—7 : 30、7 : 30—8 : 30、8 : 30—9 : 30，为与城市路网的实际运行相符合，将中间时段设为出行高峰期 ( 拥堵时段 )，两端为非高峰期 ( 畅行时段 )。在城市路网中，通常将道路分成主干路、次干路和支路，不同路段上的实时速度不同，主要与道路的长度、车道数、通行能力等因素有关。为尽可能模拟实际路网，将客户点间的距离按照长度进行划分，各路段上高峰期与非高峰期对应的速度如表 2 所示。

（6）初始化种群。采用节约法、贪心算法及随机生成初始解的方法生成 3 个初始解。其中，节约法与贪心算法生成的初始解如表 3 和表 4 所示。

（7）算法控制参数。种群内个体数目为 30；交叉概率pc= 0.9；变异概率pm= 0.09；每隔 20 代进行 1 次移民操作；精华种群中最优解保持 50 代算法停止。

表1 客户坐标及需求量

表2 各路段上高峰期与非高峰期速度

表3 节约法生成初始解

表4 贪心算法生成初始解

3.2 计算结果分析

每次程序运行 136 min。Matlab 运行 5 次，5 次运行的收敛性均较好。5 次运行结果中有 2 次结果相同，舍去 1 组结果，保留 4 组运行结果，该结果与 2 组构造算法产生的局部最优解进行比较，最优解比较表如表 5 所示。通过比较分析，选取最优的 1 组作为算例最优解，最优解车辆成本为 18 000元，即需要 18 辆车，时间成本为 2 033.97 元，碳排放成本为 9 194.023 元，总成本为 23 963.59 元，最优解相关指标、最优路径规划图分别如表 6 和图 4 所示，图 4 中每种颜色的线条代表 1 辆车服务客户点的旅行路径，共有 18 种颜色，分别代表 18辆车。

表5 MPGA4 组运行结果与 2 组局部最优解比较表

表6 EVRP 模型最优解相关指标

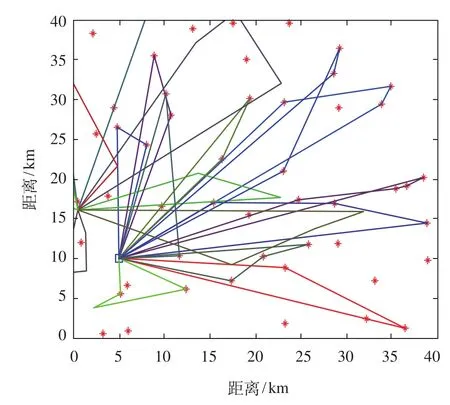
图4 EVRP 模型最优解规划图

4 结束语

在研究 1 种新车辆路径问题时，通过考虑碳排放的车辆路径问题 ( EVRP )，构建基于时间依赖车辆路径问题模型 ( TDVRP )，将碳排放、车辆数和旅行时间最少共同作为模型的目标函数，并且首次将该模型与快递企业的配送特殊性相结合，应用到快递企业配送路径选择中。通过设计适合该模型的多种群遗传算法求解模型，以某快递企业在成都市的网点布局和早高峰配送数据为例进行算例分析，结果表明 MPGA 用于求解 EVRP 问题具有良好的收敛性和时间特性，这对快递企业低碳配送路径选择具有重要意义。

[1] 张洪斌. 我国快递业现状和发展趋势预测[J]. 中国物流与采购，2006，8(9)：34-37

[2] 中国电子商务研究中心. 2013(上)中国电子商务市场数据监测报告[M]. 杭州：中国电子商务研究中心，2013.

[3] FigliozziI M A. The Impacts of Congestion on Commercial Vehicle Tour Characteristics and Costs [J]. Forthcoming Transportation Research Part E：Logistics and Transportation，2009(46)：496-506.

[4] Miguel Figliozzi. Emissions Minimization Vehicle Routing Problem[J]. Transportation Research Board，2010(1)：10-14.

[5] Meead Saberi，I Omer Verbas. Continuous Approximation Model for the Vehicle Routing Problem for Emissions Minimization at the Strategic Level [J]. Journal of Transportation Engineering，2012(138)：1368-1376.

[6] 杨子岳. 低碳视角下B2C电子商务配送路径优化研究[D]. 成都：西南交通大学，2012.

[7] Malandraki C，Daskin M S. Time-dependent Vehicle-routing Problems-formulations，Properties and Heuristic Algorithms[J]. Transportation Science，1992，26(3)：185-200.

[8] 周 冬. 基于TDVRP和STDVRP模型的金融押运车辆路径问题研究[D]. 北京：清华大学，2010.

[9] 史 峰，王 辉，郁 磊，等. Matlab智能算法30个案例分析[M]. 北京：北京航空航天大学出版社，2011.