基于可变精度粗糙集模型的有导师机器学习

李海霞

基于可变精度粗糙集模型的有导师机器学习

李海霞

（莆田学院 信息工程学院，福建莆田 351100）

机器学习是人工智能领域中重要的研究课题，基于经典粗糙集的机器学习，只有学习者的分类被完全包含在导师的分类中时，才形成决策规则，条件比较苛刻；而基于可变精度粗糙集理论的有导师机器学习，根据学习者的分类包含在导师的分类中的包含度αi，与事先给定的精度系数β的比较，来求取具有一定相容性的决策规则，该方法更具有灵活和实用性。

粗糙集；可变精度粗糙集；导师；机器学习；人工智能

机器学习是人工智能领域中重要的研究课题，粗糙集理论［1］可以作为机器学习中研究某些问题的理论基础。有导师学习［1-2］是一种从例子中学习的方法，导师具有某一论域U的知识，能够对论域的元素进行分类，学习者的任务是学习导师的知识。也就是学习者要利用导师提供的能够分类的例子，根据他们的特征，从中导出相容决策规则，即从决策表导出相容决策算法。在决策表中，条件属性就是学习者的属性，决策属性就是导师的属性。

Pawlak提出的粗糙集模型处理的分类必须是完全正确的或肯定的，但实际应用中，数据中包含噪音是难免的，为了提高在实际应用中对噪音数据的适应能力，Ziarko［3-4］提出了可变精度粗糙集模型，简称VPRS模型。

本文介绍的基于可变精度粗糙集模型［5-7］的有导师机器学习，把从决策表导出相容决策算法的条件由粗糙集的绝对包含弱化为可变精度粗糙集的多数包含，这样从决策表导出的决策算法允许一定的错误分类率存在，使得机器学习更符合实际、更具灵活性。

1 可变精度粗糙集模型

定义1 设X和Y为论域U的非空子集，0≤α≤1，定义包含度关系：

当0.5＜α≤1，则定义了Y对X的α—多数包含度关系，即X中有50%以上的元素被Y包含（或X与Y的公共元素占X的50%以上）。多数包含关系允许一定程度的错误分类率存在，或者说具有一定的容错能力，α体现了多数包含程度，1-α体现了误分类率。

定义2 给定论域U，不可分辨关系R⊆U×U，X⊆U，β∈（0.5，1］，则

分别称为X关于R的β下近似，X关于R的β上近似。

可变精度粗糙集模型通过设置精度系数β，放宽了经典粗集理论对边界的严格定义。柔化了边界。通常β的取值有两种方式，Ziarko把β定义为分类误差率［3］，β的取值范围为［0.0，0.5），而An等人定义β为分类正确率［8］，β的取值范围为［0.5，1），这里采用An等人的定义方式。

可变精度体现在β的可变上。根据β的取值不同，得到的X关于R的β下近似、上近似不同。

由定义2可以看出，可变精度粗糙集模型的近似定义是基于多数包含的。

为了便于与经典粗糙集比较，在此将经典粗糙集的上、下近似用包含度定义如下

定义3 给定论域U，不可分辨关系R⊆U×U，X⊆U，则：

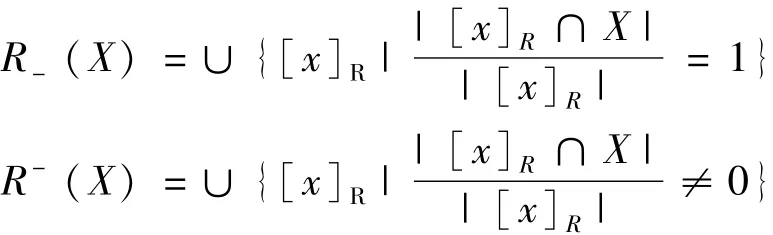
分别称为X关于R的下近似，X关于R的上近似。

由定义2与定义3比较可知，经典粗糙集模型建立在绝对包含的基础上，它是可变精度粗糙集模型在最大包含即β=1时的特例，但β=1与β＜1在对分类的影响上有很大的本质区别。通过引入可变精度粗糙集模型，利用包含度（来描述有导师机器学习中，学习者学习导师知识的程度。当α≥β时，可导出有一定容错能力的相容决策规则。α可视为规则的相容度、机器学习程度。

2 基于可变精度粗糙集的有导师机器学习

在机器学习中，有导师学习是一种从例子中学习的方法。导师具有某一论域U的知识，学习者的任务是学习导师的知识。也就是学习者要利用导师提供的能够分类的例子，根据他们的特征，从中导出相容决策规则。按照粗集理论的说法，有导师学习就是从决策表导出相容决策算法。在决策表中，条件属性就是学习者的属性，决策属性就是导师的属性。本文介绍的基于可变精度粗集的机器学习，把从决策表导出相容决策算法的条件由粗集的绝对包含弱化为可变精度粗集的多数包含。

基于经典粗糙集的有导师机器学习，当导师分类的下近似为（时，学习者无法学习导师的知识。针对此，本文引入了基于可变精度粗糙集的有导师机器学习，当经典粗糙集中导师分类的下近似为（时，可以根据导师分类包含学习者分类的包含度（（学习者学习导师知识的程度），以及实际可接受的错误分类率β，推出具有一定容错能力的相容决策规则。

下面的例子对基于粗糙集的有导师机器学习和基于可变精度粗糙集的有导师机器学习作了比较。基于可变精度粗糙集的有导师机器学习中，当学习者学习导师的知识的程度很大时，可以粗略地认为，学习者学习了导师的所有知识。

例 如表1所示。论域由8个研究对象构成，每一个对象都由学习者属性C=｛a，b，c｝的集合描述，学习者的属性分别表示为Va=｛高，矮｝，Vb=｛黑，红，黄｝，Vc=｛蓝，棕｝。根据导师的分类，每一个对象被分成“+”或“-”类，因此导师属性值Ve=｛+，-｝，它代表了学习者基于C的属性值要学习的概念。

表1 某一知识表达系统

解 以学习者的属性｛b｝，导师的属性值｛+｝为例，其他情况类似。

首先看看基于经典粗糙集的学习情况：

根据学习者属性｛b｝的划分：

U/ind（b）=｛x1=｛1，2，3｝，x2=｛4，6｝，x3=｛5，7，8｝｝

des（x1）=（头发：黑）

des（x2）=（头发：红）

des（x3）=（头发：黄）

导师的划分：

U/ind｛e｝=｛y1=｛1，4，5，7｝，y2=｛2，3，6，8｝｝

des（y1）=（分类：+）

des（y2）=（分类：-）

首先求xi（i=1，2，3）｛头发｝与y1｛+｝的包含度，根据定义1：

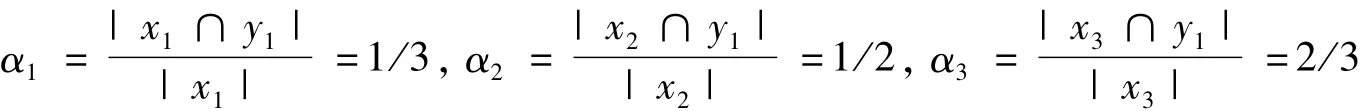
根据定义3，由于包含度αi≠1（i=1，2，3），即导师分类y1的下近似为Φ，故没有相容规则。根据基于经典粗糙集的有导师机器学习，学习者无法学习导师的知识。

下面通过可变精度粗糙集，来看一下学习者的学习情况。

根据定义2，比较包含度αi与精度系数β∈（1/2，1］（β根据可接受的错误分类率，事先给定）的大小，若αi≥β，则形成相容决策规则，其中的αi定义为该规则的相容度，机器学习的学习程度。

如果取β=0.6，根据求得的包含度αi和给定的β比较，则只有（α3=2/3）≥（β=0.6），即y1的（下近似为x3，故规则：（头发：黄）→（e：+）在允许一定的错误分类的情况下是相容的，即可学习的。

如果取β=0.8，则y1的β下近似为Ø，则所有规则都是不相容的、学习者无法学习导师的知识。

由此可以看出，基于可变精度粗糙集模型的有导师机器学习，允许一定的错误分类率存在，能够导出具有一定相容度的决策规则。更符合实际、更具灵活性。

3 学习算法

给定某一知识表达系统K=（U，C，D）（U为论域，C为学习者属性，D为导师属性），和精度系数β∈（1/2，1］

1）分别求学习者属性的划分xi和导师的划分yj；

2）根据定义1，求xi与yj的包含度αij；

3）求出满足αij≥β的决策规则。该决策规则是相容度为αij的决策规则。

4 结语

基于可变精度粗糙集的有导师机器学习，根据学习者的分类包含在导师的分类中的包含度αi，与事先给定的精度系数β值的比较，来求取具有一定相容性的决策规则，从而能够更深层次地理解并更好地利用数据特性。正是由于β的取值，导致了一定程度的错误分类率的存在。通过上面例子的比较，可以看出，基于可变精度粗糙集的有导师机器学习更具有灵活性和实用性。根据实际情况，来选取β∈（0.5，1］值，获取具有不同程度相容性的决策规则。

［1］ 曾黄麟.粗集理论及其应用［M］.重庆：重庆大学出版社，1995.

［2］ 吴武琴，高晓红，刘文奇.一种改进的基于粗糙集理论的有导师学习方法［J］.昆明理工大学学报：理工版，2008，33（3）：122-124.

［3］ ZiarkoW.Variable precision rough setmodel［J］.Journal of computer and System Science，1993，46：39-59.

［4］ Ziarko W.Analysis of uncertain information inthe framework of variable precision rough sets［J］.Foundations of Computing and Decision Sciences，1993，18：381-396.

［5］ 王加阳，陈松乔，罗安.可变精度粗集模型研究［J］.计算机与数字工程，2005，33（8）：53-54.

［6］ 杨习贝，杨静宇，於东军，等.不完备信息系统中的可变精度分类粗糙集模型［J］.系统工程理论与实践，2008，5：116-121.

［7］ 张明，唐振民，徐维艳，等.可变粒度粗糙集［J］.计算机科学，2011，10（38）：220-247.

［8］ AN A，Shan N，Chan C N，et al.Discovering rules forwater demand prediction：an enhanced rough-setapproach［J］.Engineering Application and Artificial Intelligence，1996，9（6）：645-653.

Supervised Machine Learning Based on Variable Precision Rough Set Theory

LIHa i-x ia

（Department of Information，Science and Engineering Putian University，Putian 351100，China）

Machine learning is an important ruestion for discussion in the Artificial intelligence.Based on classical rough set，and with learner’s classification completely included in the tutor’s classification，Machine learning can form decision rule.The condition is very rigorous.Rather，Supervised machine learning based on variable precision rough set theory obtains certain compatibility decision rules according to the comparison of the inclusion degreeαithat learners’classification is included in the tutor’s classification with the given the precision coefficientβ.This method is more flexible and practical.

rough set；variable precision rough set；tutor；machine learning；artificial intelligence

TP181

符：A

1009-0312（2014）03-0050-04

2013-12-26

李海霞（1980—），女，甘肃庄浪人，讲师，硕士，主要从事人工智能与数据挖掘、粗糙集方面研究。