一类反常次扩散方程Neumann问题的有限差分格式及收敛性分析
2014-07-12马亮亮刘冬兵
马亮亮,刘冬兵
(攀枝花学院 数学与计算机学院,四川 攀枝花 617000)
一类反常次扩散方程Neumann问题的有限差分格式及收敛性分析
马亮亮,刘冬兵
(攀枝花学院 数学与计算机学院,四川 攀枝花 617000)
利用一阶向前差商和空间二阶中心差商以及高阶线性多步法公式构造了反常次扩散方程Neumann问题的有限差分格式,借助Fourier分析方法对差分格式的稳定性进行了分析,并讨论了差分格式的误差和收敛性问题.
反常次扩散方程;差分法;分离变量法
整数阶扩散方程不能准确地描述自然界和工程技术领域中存在的许多反常扩散现象,分数阶导数被证明能够较精确地描述有记忆和遗传以及依赖性质的物理过程,因而成为反常扩散现象物理力学建模的有力工具[1-3]. 近年来,国内外一些专家和学者在分数阶扩散方程衍生方程的理论分析、数值算法、工程应用等方面做了非常有意义的研究工作:Yuste等[4]对反常次扩散问题提出了一种显式有限差分方法和一种新Von Neumann类型的稳定性分析;Langlands等[5]对反常次扩散问题提出了一种隐式近似格式(L1近似),并讨论了差分格式的精度和稳定性;Zhuang等[6]提出了一种隐式差分方法和分析技巧求解时间分数阶反常次扩散方程,利用能量方法给出了稳定性和收敛性的详细证明;Chen等[7]利用新的Fourier方法,讨论了时间分数阶反常次扩散问题.
本文考虑如下带有Neumann边界条件的非齐次反常次扩散方程:

其中,0<α<1,Kα是扩散系数,q(x,t)为充分光滑的函数,表示关于t的(1-α)阶Riemann-Liouville分数阶微分算子:

1 有限差分格式
定义1[8]93Mittag-Leffler函数是指数函数的自然推广,其单参数的形式为:
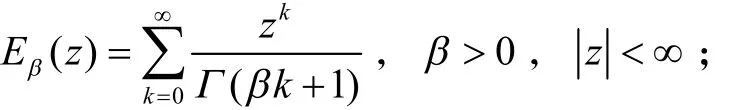
双参数的形式为:
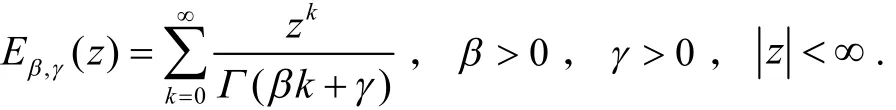
定义2[8]216-217μ表示Riemman-Liouville分数阶积分算子,分数阶线性多步法对应1~6阶方法的生成函数如下:

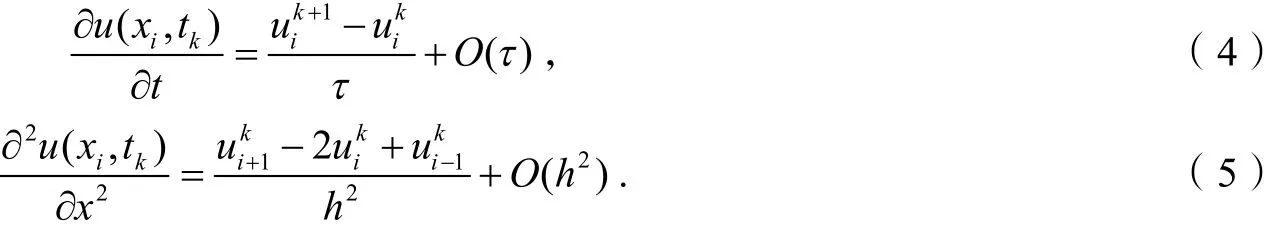
将式(4)和式(5)代入式(1),得:
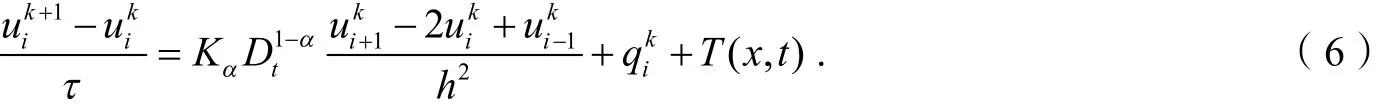
其中,T(x,t)为截断误差.
对于分数阶导数的离散,采用如下高阶线性多步法:
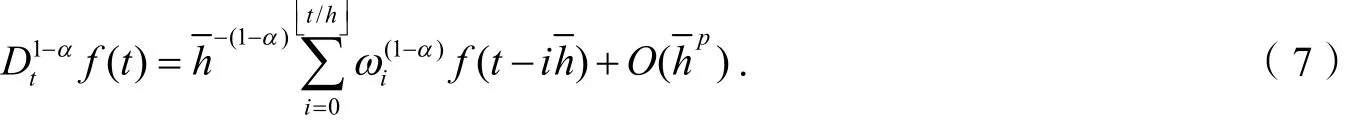
将式(6)和式(7)代入方程(1)并舍去截断误差得:

2 稳定性与收敛性分析
2.1 稳定性分析


若存在δ使得ξ>1,则差分格式(8)不稳定.
考虑极限情况ξ=-1,则
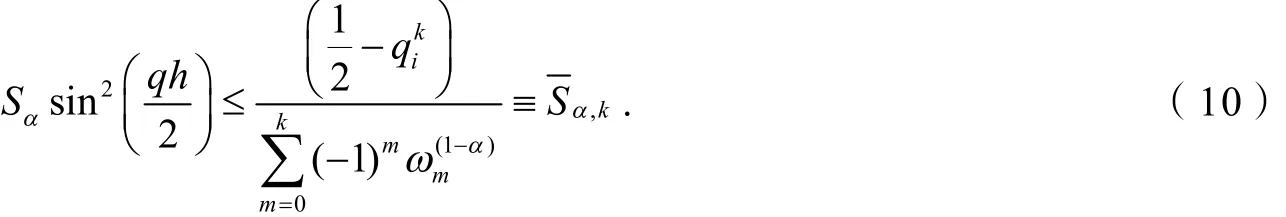
因此,要使差分格式(10)稳定,需满足以下条件:
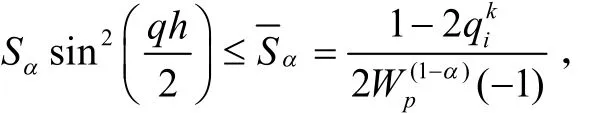
2.2 误差分析

又因为
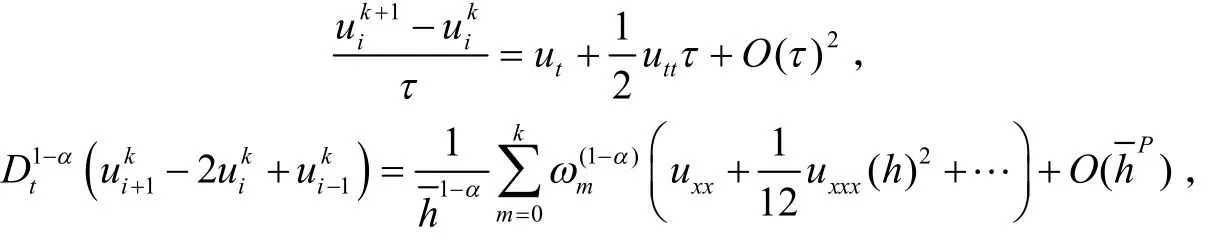
所以:

因此,假设:1)u的初边值条件相容,2)u在初始点t=0处充分光滑,则差分格式(8)无条件收敛. 即
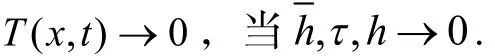
3 数值例子
考虑如下带有Neumann边界条件的非齐次反常次扩散方程:
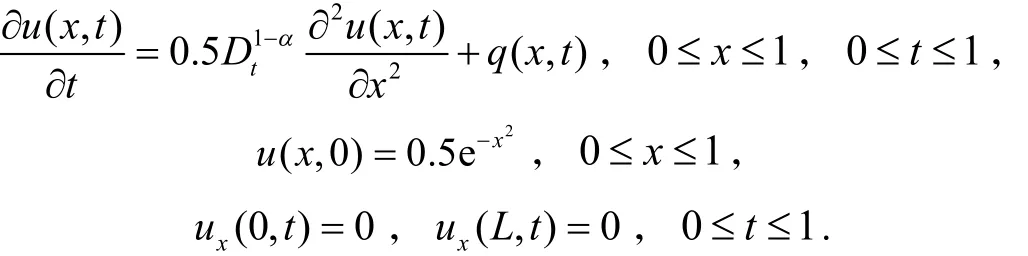
其中,α=0.6,f(x,t)=-(1+x)(1+t2). 此方程有精确解:

解 取定时间步长τ=0.0001,空间步长h=0.02. 图1是在t=0.01时刻由隐式差分格式(8)计算得到的数值解与精确解的平面图,可以看出数值解收敛于精确解. 图2是隐式差分格式(8)计算得到的数值解与空间轴、时间轴之间的三维立体图,从图中可以看出时间分数阶对扩散性态的影响.
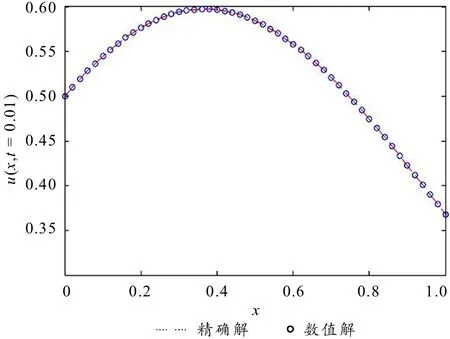
图1 数值解与精确解比较图

图2 三维立体图
[1] 孙洪广,陈文,蔡行. 空间分数阶导数“反常”扩散方程数值算法的比较[J]. 计算物理,2009, 26(5): 719-724.
[2] ANDRADE de M F, LENZI E K, EVANGELISTA L R, et al. Anomalous diffusion and fractional diffusion equation: anisotropic media and external forces [J]. Physics Letters A, 2005, 347(4-6): 160-169.
[3] PODLUBNY I. Fractional differential equations [M]. San Diego: Academic Press, 1999.
[4] YUSTE S, ACEDO L. An explicit finite difference method and a new Von Neumann-type stability analysis for fractional diffusion equations [J]. SIAM J Numer Anal, 2005, 42(5): 1862-1874.
[5] LANGLANDS T, HENRY B. The accuracy and stability of an implicit solution method for the fractional diffusion equation [J]. J Comp Phys, 2005, 205(2): 719-736.
[6] ZHUANG Pinghui, LIU Fawang, ANH V, et al. New solution and analytical techniques of the implicit numerical method for the anomalous sub-diffusion equation [J]. SIAM on Numerical Analysis, 2008, 46(2): 1079-1095.
[7] CHEN Changming, LIU Fawang, TURNER I, et al. A Fourier method for the fractional diffusion equation describing sub-diffusion [J]. J Comp Phys, 2007, 227: 886-897.
[8] 郭柏林,蒲学科,黄凤辉. 分数阶偏微分方程及其数值解[M]. 北京:科学出版社,2011.
[责任编辑:熊玉涛]
A Finite Difference Scheme and a Convergence Analysis of a Kind of Anomalous Diffusion Equation with Neumann Conditions
MA Liang-liang, LIU Dong-bing
(College of Mathematics and Computer Science, Panzhihua University, Panzhihua 617000, China)
A finite difference method and a convergence problem for a kind of anomalous diffusion equation with Neumann conditions are discussed. A finite difference scheme is obtained by adopting the method of the first-order forward difference quotient and second-order space center difference quotient and the formula of higher-order linear multistep method to discrete the fractional derivatives. The stability of the difference scheme is analyzed by means of Fourier analysis and the errors and convergence of the schemes are also discussed.
anomalous diffusion equations; difference methods; separation variable methods
O241.82
A
1006-7302(2014)01-0001-04
2013-04-22
国家自然科学基金资助项目(No.60673192);四川省科技厅资助项目(2013JY0125)
马亮亮(1986—),男,甘肃天水人,讲师,硕士,主要从事模型优化和微分方程研究.
