非一致节点的未知复杂动态网络的自适应同步
2014-07-11郝修清李俊民
郝修清, 李俊民
(西安电子科技大学 数学与统计学院,陕西 西安 710071)
近几年来,复杂动态网络成为了一个研究热点,许多自然系统和人工系统都可以描述为复杂动态网络[1-2].在复杂动态网络的研究中,同步是受到极大关注的一个问题[3-13],具有重要的现实意义和广泛的应用前景.各种不同的控制方法被用于复杂动态网络的同步,如脉冲控制[3]、非脆弱控制[4]、牵制控制[5]和自适应控制[6]等.
从研究对象来看,复杂动态网络的同步已经从一致性节点和线性耦合发展到非一致节点[7-9]和非线性耦合[9-11].同时,关于耦合时滞和耦合强度的问题也在复杂动态网络的研究中引起了重视[6,11-13].例如,文献[9]研究了一类非线性耦合的具有非一致节点和耦合时滞的复杂动态网络的同步问题;文献[10]对非线性耦合的复杂动态网络进行了自适应牵制控制;文献[11-13]对复杂动态网络中的时变时滞和时变耦合强度进行了讨论,采用自适应律对未知的参数进行了辨识,实现了对复杂动态网络的自适应同步.可见,对复杂动态网络的研究越来越接近于现实环境.值得注意的是,目前对复杂网络是未知的情形考虑得很少.
另一方面,李雅普洛夫稳定性理论被广泛用于系统的镇定和跟踪问题[14-15].对于具有周期特性的信号,可设计自适应学习律对其进行估计,进而实现对系统的自适应学习控制[16-17].在文献[17]中,考虑一种周期时变时滞非线性参数化系统的自适应学习控制,运用对系统重构的方法,很好地解决了对周期参考信号的跟踪问题.
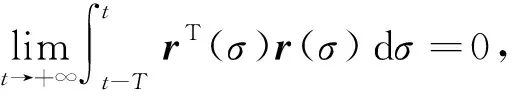
1 未知复杂动态网络的自适应同步方案
1.1 系统描述和控制目标
由N个非一致节点耦合组成的复杂动态网络系统为
(1)
其中,xi(t)=[xi1,xi2,…,xin]T∈Rn,表示第i个节点在t时刻的状态向量;fi和gij是未知的、光滑的连续向量值函数;矩阵A= (aij)n×n,表示复杂动态网络的拓扑结构或邻接矩阵,若aij≠ 0,则表示节点j对节点i的动力学行为有影响;hj(t)是未知的周期时变时滞,但其周期是已知的.
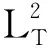
假设1 对于式(1)中的未知非线性向量值函数,假设存在li>0,cij>0,使得
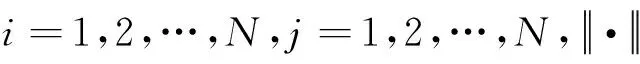
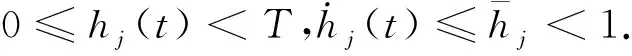
假设3 对于式(1),假设邻接矩阵A的元素满足|aij|
1.2 控制输入和周期自适应律的设计

(2)
其中,ui(t)表示每个节点的输入,此时误差方程为
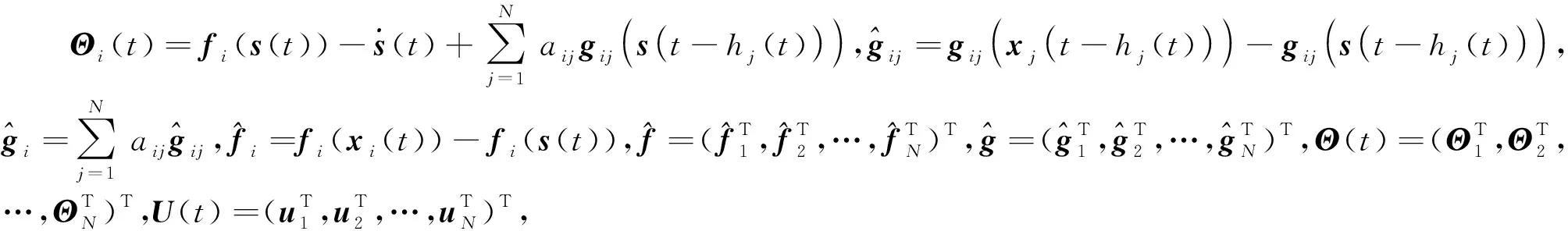
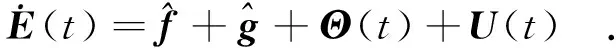
(4)
容易证明,Θ(t+T)=Θ(t).由Θ(t)的定义,可得,Θ(t)是以T为周期的周期连续向量值函数.
(5)
对式(5)求导,可得
由Young不等式和假设1,可得
将上面两个不等式代入式(6),同时由假设1~3可得
取足够大的L,满足Na2c2-L<0,有
(8)
设计控制输入和周期自适应律为
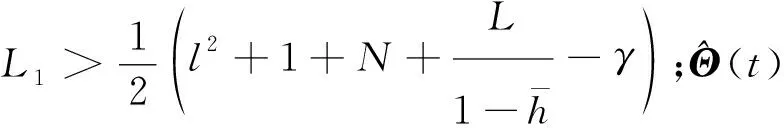
(11)
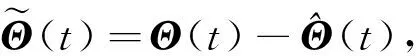
注在整个同步方案的设计中,对误差方程进行了重构,采用信号置换的思想,将耦合部分、周期时变时滞以及给定的周期参考信号整合为一个未知的周期时变向量Θ(t),在采用周期自适应律对Θ(t)进行估计的基础上,设计了简单的反馈控制.
1.3 收敛性分析
这里通过一个定理,说明复杂动态网络能够实现自适应同步,并且所有的信号都是有界的.
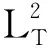
(1) 计算W(t)在1个周期上的差分,即
(12)
利用周期自适应律式(10),经过运算,式(12)的最后一项可以表示为
(13)
将式(9)和式(10)代入式(8),再将式(13)代入式(12),可得
(14)
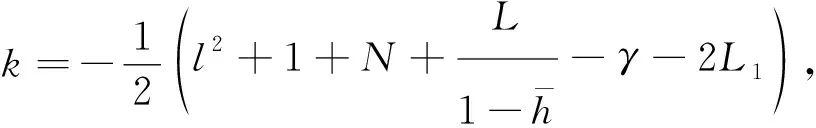
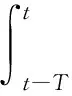
(15)
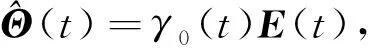
(16)
利用Young不等式,可得
(17)
把式(17)代入式(16),可得
(18)
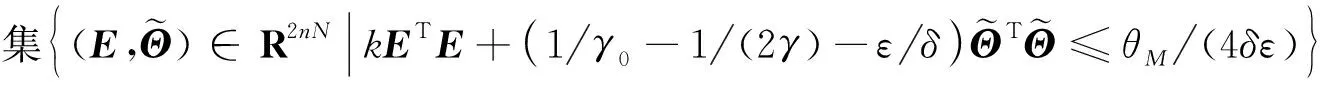
(19)


2 仿真研究
下面将给出仿真实例,以验证所设计的同步方案的有效性.
例 在系统式(2)中,取节点数N=3,每个节点状态的维数n=3,已知的周期T=2π,同步目标为:s(t)= (s1(t),s2(t),s3(t))T= (2+0.3 sint,-1-0.5 sint,0.6 cost)T,复杂动态网络各个节点处的状态方程为
(20)
其中,时变时滞h1(t)=1-0.4 sin2t,h2(t)=0.8-0.5 sin2t,h3(t)=0.7-0.6 sin2t,而非线性向量值函数为
选取系统初始状态为x1(0)=[1,0,-1]T,x2(0)=[2,1,3]T,x3(0)=[-0.5,1.2,-3]T.设计控制输入和周期自适应律为
将控制输入式(21)和周期自适应律式(22)代入复杂动态网络式(20),图1~3为复杂动态网络中各个节点的状态xi(t)= [xi1,xi2,xi3]T对s(t)的跟踪情形.可见,即使在每个节点选取不同的初始状态,受控系统式(20)都可以做到同步于给定的周期轨迹s(t).
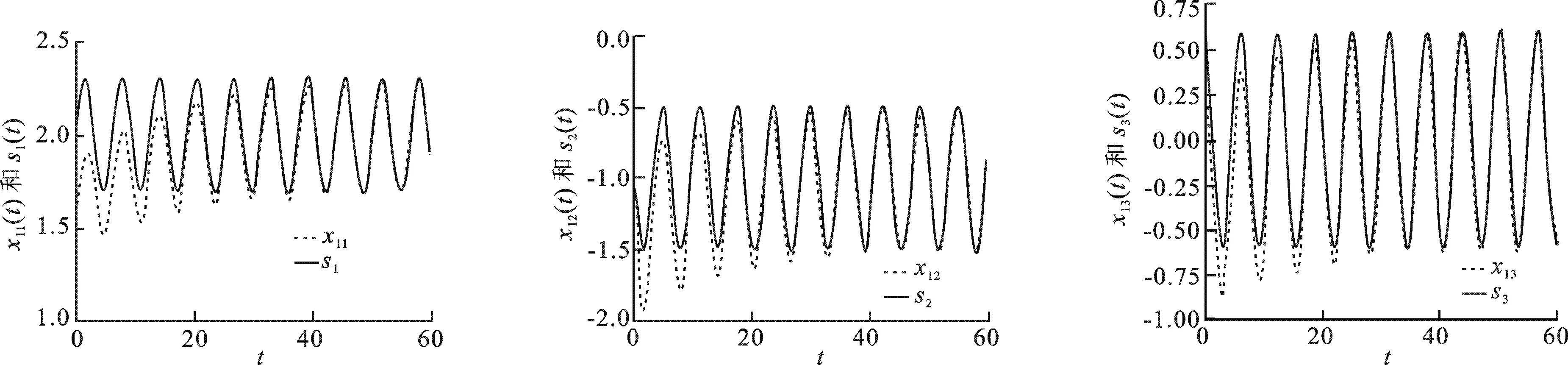
图1 x1(t)和s(t)的轨迹(从左到右分别表示3个分量的轨迹)
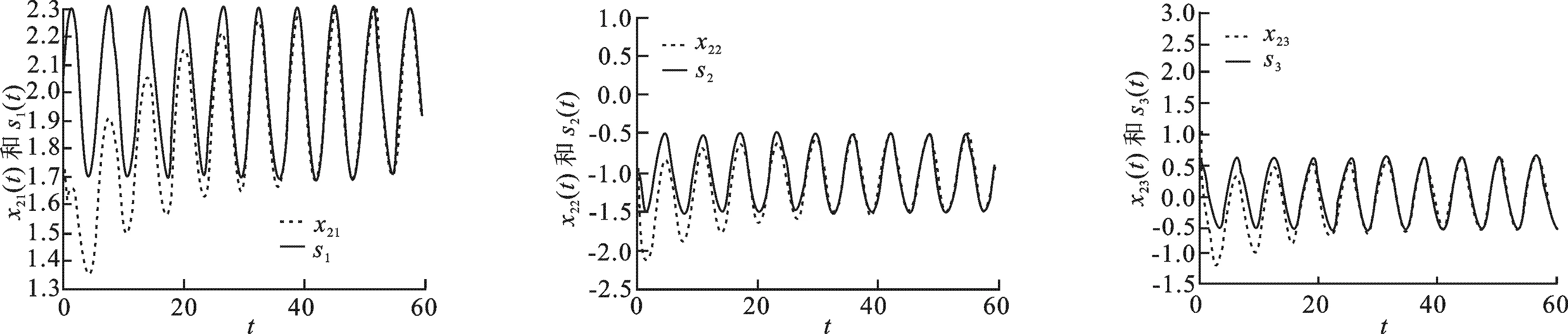
图2 x2(t) 和s(t)的轨迹(从左到右分别表示3个分量的轨迹)
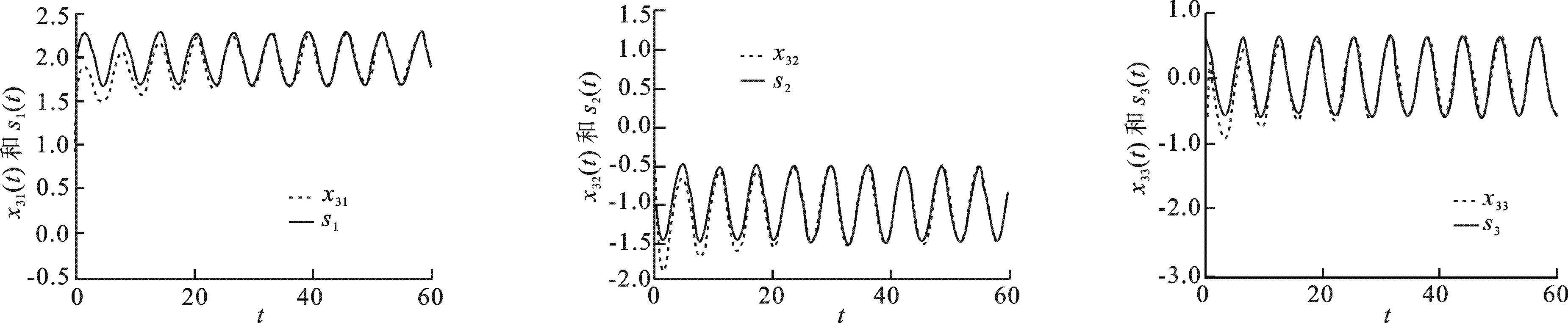
图3 x3(t) 和s(t)的轨迹(从左到右分别表示3个分量的轨迹)
3 结 束 语
考虑了非一致节点、非线性耦合、多重时变时滞的未知复杂动态网络的同步问题,通过信号置换技术对系统进行重构,设计自适应学习控制使其能够同步于任意给定的周期参考信号.将非线性和时滞等问题加入所讨论的复杂系统,同时考虑到复杂动态网络的未知性,使其更接近真实环境,具有一定的现实意义.
[1] Strogatz S H. Exploring Complex Networks [J]. Nature, 2001, 410(6825): 268-276.
[2] Newman M E J. The Structure and Function of Complex Networks [J]. SIAM Review, 2003, 45(2):167-256.
[3] Zhang Qunjiao, Chen Juan, Wan Li. Impulsive Generalized Function Synchronization of Complex Dynamical Networks [J]. Physics Letters A, 2013, 377(39): 2754-2760.
[4] 李俊民, 曹梦涛, 沈思. 时变复杂动态网络非脆弱同步算法[J]. 西安电子科技大学学报, 2012, 39(5): 119-125.
Li Junmin, Cao Mengtao, Shen Si. Non-fragile Synchronization Algorithm for Complex Time-varying Dynamical Networks [J]. Journal of Xidian University, 2012, 39(5): 119-125.
[5] Wu Xiangjun, Lu Hongtao. Hybrid Synchronization of the General Delayed and Non-delayed Complex Dynamical Networks via Pinning Control [J]. Neurocomputing, 2012, 89: 168-177.
[6] Guo Xiaoyong, Li Junmin. A New Synchronization Algorithm for Delayed Complex Dynamical Networks via Adaptive Control Approach [J]. Communications in Nonlinear Science and Numerical Simulation, 2012, 17(11): 4395-4403.
[7] Fan Yongqing, Wang Yinhe, Zhang Yun, et al. The Synchronization of Complex Dynamical Networks with Similar Nodes and Coupling Time-delay [J]. Applied Mathematics and Computation, 2013, 219(12): 6719-6728.
[8] Wu Xiangjun, Lu Hongtao. Projective Lag Synchronization of the General Complex Dynamical Networks with Distinct Nodes [J]. Communications in Nonlinear Science and Numerical Simulation, 2012, 17(11): 4417-4429.
[9] Wang Yangling, Cao Jinde. Cluster Synchronization in Nonlinearly Coupled Delayed Networks of Non-identical Dynamic Systems [J]. Nonlinear Analysis: Real World Applications, 2013, 14(1): 842-851.
[10] Jin Xiaozheng, Yang Guanghong. Adaptive Pinning Synchronization of a Class of Nonlinearly Coupled Complex Networks [J]. Communications in Nonlinear Science and Numerical Simulation, 2013, 18(2): 316-326.
[11] Wang Tengfei, Li Junmin, Tang Shu. Adaptive Synchronization of Nonlinearly Parameterized Complex Dynamical Networks with Unknown Time-Varying Parameters [J]. Mathematical Problems in Engineering, 2012, 2012: 592539.
[12] Ji D H, Jeong S C, Park J H, et al. Adaptive Lag Synchronization for Uncertain Complex Dynamical Network with Delayed Coupling [J]. Applied Mathematics and Computation, 2012, 218(9): 4872-4880.
[13] Guo Xiaoyong, Li Junmin. Stochastic Adaptive Synchronization for Time-varying Complex Delayed Dynamical Networks with Heterogeneous Nodes [J]. Applied Mathematics and Computation, 2013, 222: 381-390.
[14] Rao Ruofeng, Wang Xiongrui, Zhong Shouming, et al. LMI Approach to Exponential Stability and Almost Sure Exponential Stability for Stochastic Fuzzy Markovian-Jumping Cohen-Grossberg Neural Networks with Nonlinear p-Laplace Diffusion [J]. Journal of Applied Mathematics, 2013, 2013: 396903.
[15] Rao Ruofeng, Zhong Shouming, Wang Xiongrui. Stochastic Stability Criteria with LMI Conditions for Markovian Jumping Impulsive BAM neural Networks with Mode-dependent Time-varying Delays and Nonlinear Reaction-diffusion [J]. Communications in Nonlinear Science and Numerical Simulation, 2014, 19(1): 258-273.
[16] Xu Jianxin, Tan Ying. A Composite Energy Function-based Learning Control Approach for Nonlinear Systems with Time-varying Parametric Uncertainties [J]. IEEE Transactions on Automatic Control, 2002, 47(11): 1940-1945.
[17] 陈为胜, 王元亮, 李俊民. 周期时变时滞非线性参数化系统的自适应学习控制 [J].自动化学报, 2008, 34(12): 1556-1560.
Chen Weisheng, Wang Yuanliang, Li Junmin. Adaptive Learning Control for Nonlinearly Parameterized Systems with Periodically Time-varying Delays [J]. Acta Automatica Sinica, 2008, 34(12): 1556-1560.
