一种多参考接收站下的时差定位算法
2014-07-11朱国辉冯大政
朱国辉, 冯大政, 周 延
(西安电子科技大学 雷达信号处理国家重点实验室,陕西 西安 710071)
无源定位技术在雷达[1]、声纳[2]、导航[3]、无线通信和传感器网络[4]等领域有着广泛的应用,是信号处理的一个重要研究方向.常用的无源定位技术包括基于到达时间差、基于到达时间和基于到达角的定位算法[5-8].其中,多站情况下的基于时差的定位技术对接收系统的要求较低,具有定位成本低、精度较高等优点,因而受到越来越多的关注.

图1 基于多参考接收站的时差定位示意图
目前常见的基于时差的多站无源定位算法有泰勒级数法[9]、牛顿法[10]、SI算法[11]、Chan算法[12]等.泰勒级数法和牛顿法是一类需要初始估计位置的递归算法,当用一组较为接近真实值的初始值进行迭代时,能快速收敛,定位精度高;但是在初始值选择不好的情况下,容易落入到局部极小点,而且收敛性难以保证.SI算法将时差定位问题转化为二次多项式求解问题,根的选取对定位结果影响很大[13];Chan算法利用两步加权最小二乘估计对辐射源位置进行定位解算;它们都是基于单参考接收站的无源定位方法.GS算法[13]是一种基于多参考接收站的时差定位算法,该算法利用基于多参考接收站的时差测量值对Chan算法中的伪线性方程组做了扩展,并进行了一步最小二乘估计,但是它没有考虑伪线性方程组中各方程对应的权重,也没有考虑最小二乘解中各分量之间的相关性.为此,笔者提出了一种新的基于多参考接收站的时差定位算法,该算法运用加权最小二乘估计对伪线性定位方程组进行初始求解,并利用初始解中各分量之间的相关性得到多组辐射源位置的估计,然后取这些估计的平均值得到最终定位结果.计算机仿真结果证实了该算法的有效性.
1 基于多参考接收站的时差定位模型
图1为三维空间中基于多参考接收站的时差定位示意图.假定任意分布的N个接收站, 第i个接收站的坐标si= [xi,yi,zi]T,辐射源位置坐标u= [x,y,z]T.
辐射源u到接收站si的距离为
ri=((u-si)T(u-si))1/2,i=1,…,N.
(1)
不妨选取s1,…,sM作为参考接收站,不考虑非视距传播的影响,根据时差定位原理,可得
(2)

用c同时乘以方程(2)两端,可将时间差方程转化为相应的距离差方程:
(3)
其中,ni,j=cΔti,j,表示相应的距离差测量误差.基于多参考接收站的时差定位问题即为根据非线性方程组(3)尽可能准确地估计辐射源位置坐标u.
2 基于多参考接收站的时差定位新算法
由式(1)可知,式(3)是关于辐射源u的高度非线性方程,为此采用两级加权最小二乘估计求解基于多参考接收站的时差定位问题.
2.1 第1级加权最小二乘估计
将式(3)右端第2项rj移至左端,两边同时平方,得
(4)

(5)
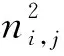
(6)
其中,ηj可以近似表示为ηj≈Bjnj,Bj=diag{rM+1,…,rN},nj=[nM+1,j,…,nN,j]T.

(7)
对近似方程G1u1≈h1,进行加权最小二乘估计求解,可得
(8)

2.2 第2级加权最小二乘估计

(11)
(12)
根据式(11)、(12)可得方程
(13)

其中,ej表示第j个元素为1,其余元素为零的M维列向量.
对近似方程G2u2j≈h2j进行加权最小二乘估计求解,可得
(17)
(18)

P-P子网络的构成要素为协同成员以及协同成员之间的关联关系,其中,协同成员为P-P子网络的节点,协同成员间的关联关系为网络的边。由此,定义P={pi|i=1,2,,n}为协同成员集合,pi表示P-P子网络中的第i个协同成员,n为网络中协同成员的数量。EP-P={(pi,pj)|θ(pi,pj)=1;pi,pj∈P}为P-P子网络中边的集合,布尔变量θ(pi,pj)表示协同成员pi与pj间是否存在关联关系。若θ(pi,pj)=1,则表示协同成员pi与pj存在关联关系;反之,则有θ(pi,pj)=0。综上,P-P子网络GP-P可以表示为
(19)
2.3 基于多参考接收站的克拉美罗界
克拉美罗界是所有无偏估计所能达到的下界,它等于Fisher信息矩阵的逆[12].令fi,j=ri-rj,将式(3)写成矢量形式为
(20)
其中,f(u)=[fM+1,1,…,fN,1,…,fM+1,M,…,fN,M]T.根据式(20)可得似然函数
(21)
其中,K为常数,Fisher信息矩阵定义为
(22)
其中,∂f(u)/∂uT的第(N-M)×(j-1)+1行至第(N-M)×(j-1)+N-M行组成的块矩阵为
3 仿真与性能分析
为了检验文中算法对辐射源位置估计的性能,进行了下述的仿真实验,并将该算法与SI、Chan、GS算法及克拉美罗界的仿真结果进行比较.
(25)
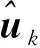

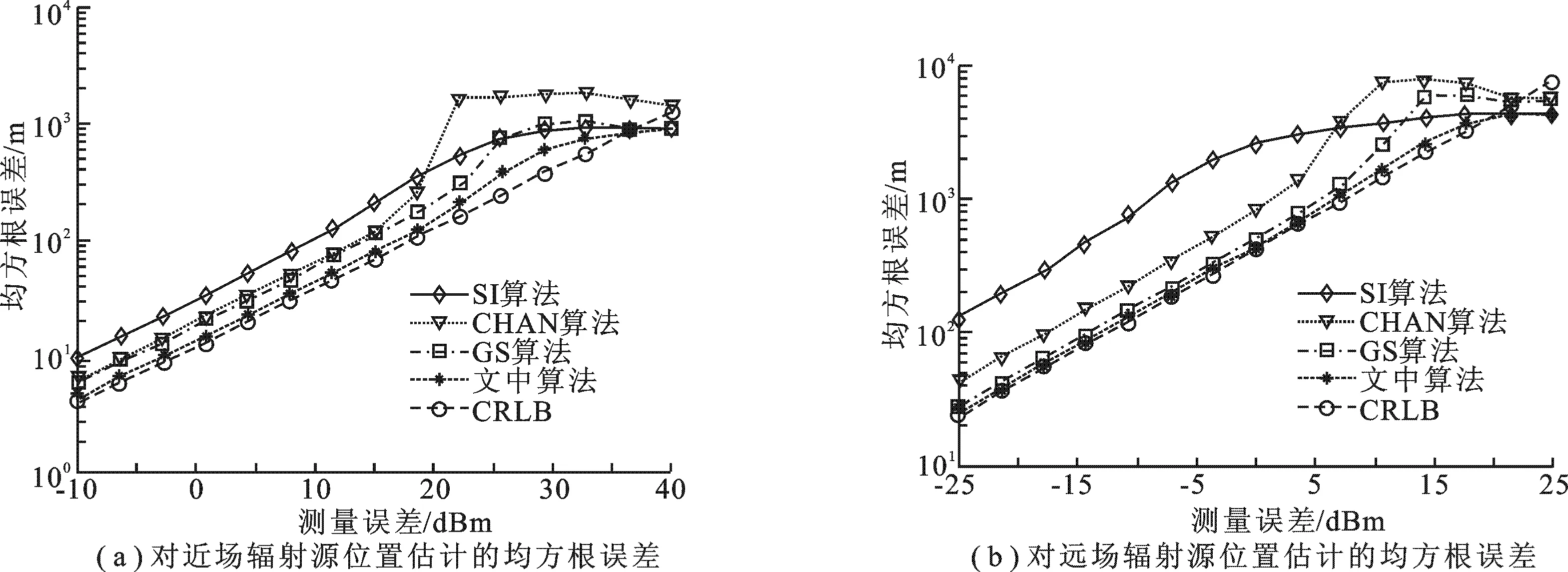
图2 各算法在M=2时对近场和远场辐射源的定位性能比较


图3 各算法在M=3时对近场和远场辐射源的定位性能比较
文中算法定位精度较高的原因在于其结合了Chan和GS算法的优点.与基于单参考接收站的Chan算法相比,文中算法也利用了两级加权最小二乘估计,不同之处在于其利用了更多的时差信息,对Chan算法中的伪线性方程组做了扩展,并且在第2级加权最小二乘估计中得到多个改进的位置估计.与基于多参考接收站的GS算法相比,文中算法考虑了方程所对应的权重,以及初始解中各分量之间的相关性,运算量因此会增加,但从图2和图3中可以看出定位精度有较大幅度提高.而SI算法将定位问题转化为二次多项式求解问题,当两根均为正数或出现复数解时,根的选取对定位结果影响很大.仿真试验中笔者选取了较好的根,但定位精度不够理想,即使测量误差较小时也可能出现很大的均方根误差.
4 结 束 语
笔者提出了一种基于多参考接收站的时差定位算法,并给出了克拉美罗界的推导过程.该方法采用基于多参考接收站的时差定位模型,运用两级加权最小二乘估计对辐射源位置进行定位解算,并充分利用了初始解中各分量之间的关系.该算法具有解析解,相对于传统的进行迭代求解的算法具有实时计算的优点.实验结果表明该算法对近场和远场辐射源均具有较好的定位精度.
[1] Jiang Min, Niu Ruixin, Blum R S. Bayesian Target Location and Velocity Estimation for Multiple-input Multiple-output Radar [J]. IET Radar, Sonar and Navigation, 2011, 5(6): 666-670.
[2] Flückiger M, Neild A, Nelson B J. Optimization of Receiver Arrangements for Passive Emitter Localization Methods [J]. Ultrasonics, 2012, 52(3): 447-455.
[3] Win M Z, Conti A, Mazuelas S, et al. Network Localization and Navigation Via Cooperation [J]. IEEE Communications Magazine, 2011, 49(5): 56-62.
[4] Gholami M, Cai Ningxu, Brennan R W. Evaluating Alternative Approaches to Mobile Object Localization in Wireless Sensor Networks with Passive Architecture [J]. Computers in Industry, 2012, 63(9): 941-947.
[5] 牛新亮, 赵国庆, 刘原华, 等. 低空目标高精度无源时差定位方法 [J]. 西安电子科技大学学报, 2009, 36(5): 862-866.
Niu Xinliang, Zhao Guoqing, Liu Yuanhua, et al. High Precision Passive TDOA Location Method for Low-altitude Targets [J]. Journal of Xidian University, 2009, 36(5): 862-866.
[6] Annibale P, Filos J, Nyalor P, et al. TDOA Based Speed of Sound Estimation for Air Temperature and Room Geometry Inference [J]. IEEE Transactions on Audio, Speech, Language and Signal Processing, 2013, 21(2): 234-246.
[7] Cheung K W, So H C. A Multidimensional Scaling Framework for Mobile Location Using Time-of-arrival Measurements [J]. IEEE Transactions on Signal Processing, 2005, 53(2): 460-470.
[8] 同非, 王俊, 李红伟. Memetic优化的外辐射源雷达方位-多普勒定位方法 [J]. 西安电子科技大学学报, 2012, 39(4): 46-51.
Tong Fei, Wang Jun, Li Hongwei. Novel Passive Radar Location Algorithm Based on Memetic Optimization by Using the Bearing-and-Doppler Frequency [J]. Journal of Xidian University, 2012, 39(4): 46-51.
[9] Foy W H. Position-location Solution by Taylor-series Estimation [J]. IEEE Transactions on Aerospace and Electronic Systems, 1976, 12(2): 187-194.
[10] Liu Ying, Zhang Xu, Liu Dan, et al. Study of Location Algorithm for Wireless Sensor Networks Based on Newton Iteration [J]. Advanced Materials Research, 2013, 645: 285-289.
[11] Smith J O, Abel J S. Closed-form Least-squares Source Location Estimation from Range-difference Measurements [J]. IEEE Transactions on Acoustics, Speech and Signal Processing, 1987, 35(12): 1661-1669.
[12] Chan Y T, Ho K C. A Simple And Efficient Estimator for Hyperbolic Location [J]. IEEE Transactions on Signal Processing, 1994, 42(8): 1905-1915.
[13] Gillette M, Silverman H. A Linear Closed-form Algorithm for Source Localization from Time-difference of Arrival [J]. IEEE Signal Processing Letters, 2008, 15: 1-4.
