区间参数梁结构热弹耦合效应分析
2014-07-11云永琥陈建军曹鸿钧
云永琥, 陈建军, 赵 宽, 阎 彬, 曹鸿钧
(西安电子科技大学 电子装备结构设计教育部重点实验室,陕西 西安 710071)
近年来,结构在突加热载作用下的动力响应问题引起了人们的关注.例如在航天器结构周期性进出阴影区和日照区时,其中柔性结构由于瞬态温度梯度的巨变将有可能导致热致振动[1].反之,结构的变形也会引起其热辐射边界条件的改变,从而导致结构温度场的变化,显然,此时结构的温度场与变形场是相互耦合的.但在计算精度要求不高的情况下,对于受到瞬态温变作用的结构动力学分析,通常可以忽略其热弹耦合效应,在计算中只需将温度梯度产生的热弯矩当作等效载荷引入到动力学方程中即可.如文献[2]用有限元方法对矩形板进行了热致振动分析,并通过实验验证了该方法的有效性.文献[3]对层叠板的热诱发振动进行了有限元计算.文献[4]对结构的热动力响应和热致振动等问题进行了分析.以上文献均未考虑结构变形对温度场的影响,而在计算精度要求较高的情况下,结构中热弹耦合项的作用将不能忽视.文献[5]提出了耦合系数的概念,并对梁结构进行了热弹耦合分析.在Boley工作的基础上,国内外学者相继开展了一些研究.文献[6]对功能梯度梁的热弹耦合进行了有限元分析.文献[7]利用有限元方法分析了二维平面板考虑热弹耦合的热动力响应问题,给出了热弹耦合项对响应的影响.文献[8]在考虑热弹耦合效应下,分析了Timoshenko梁同时受到热载荷和力载荷作用时的动力特性,并提出了求解耦合动力学方程的方法.文献[9]对辐射换热条件下的空间薄壁杆件的热-动力学耦合问题进行了有限元分析,得到了热载荷对结构响应的影响.
目前,在结构热弹耦合效应分析中,研究对象基本上为确定性参数模型.然而,由于结构在制造过程中的各种不确定性因素以及误差的影响,导致结构的物性参数具有一定的不确定性,并且结构所受的热载荷和力载荷有时亦具有不确定性,此时结构的动力响应也将呈现出不确定性.因此,分析结构所受载荷及其物性参数的不确定性对动力响应的影响,其结果较确定性问题的解无疑更加符合客观实际.文献[10]将不确定结构参数视为随机变量,利用随机因子法推导出结构动力响应的均值和方差的计算表达式,对随机参数弹性杆在瞬态温度场下的响应问题进行了分析.文献[11-12]利用区间分析方法对区间不确定性结构的动态特性和动态响应进行了分析.
笔者针对Euler-Bernouli梁结构,考虑其物性参数、温度和外力载荷均为区间变量,建立了其热弹耦合动力学区间有限元方程,提出了结构热弹耦合动力响应范围的区间计算方法.并通过算例证明了该方法的可行性与有效性.考察了结构的区间物性参数对梁动力响应的影响,以及结构受力变形对热弹耦合效应的影响.

图1 悬臂梁结构图
1 热弹耦合悬臂梁有限元方程的建立与求解
以图1矩形截面悬臂梁为分析对象,环境温度为T0,在t=0的初始时刻,梁的上端面同时受到阶跃均布力f和热流q的共同作用,下端面绝热,忽略固定端面的热传导和自由端截面以及前后表面的换热.由于热流在梁上端面均匀分布,沿着梁轴向任意截面上的温度处处相等,因此热流仅沿梁厚度方向传导.鉴于此,求解该梁热弹耦合动力响应将需分别构建以下两种有限元模型.
1.1 梁动力学有限元模型

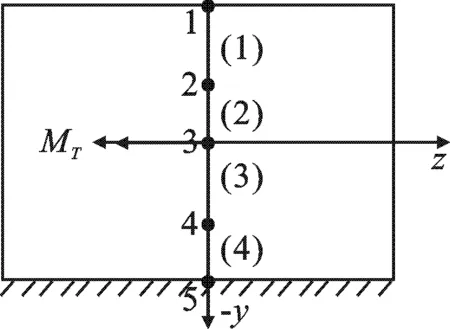
图2 热分析模型
通过对各个单元进行组集,可得梁的动力学有限元方程为[13]
(1)
其中,u为结构的位移向量,M和K分别为结构的总质量矩阵和总刚度矩阵,FB为总力载荷向量,FT为总温度载荷向量.
1.2 梁热分析有限元模型
梁热分析模型如图2所示.将梁横截面沿厚度方向离散分为m个单元和m+1个节点.由自由能密度和熵密度的计算,并利用最小势能原理,导出一维耦合热传导有限元方程为[7]
其中,T为待求的节点瞬态温度向量;C为热容矩阵;KT为热传导刚度矩阵;P为节点热载荷列阵;N为单元节点温度的形函数;B为单元节点位移应变矩阵;H为温度与弹性变形的耦合矩阵项,它表明温度场不仅与热源、热力学物性参数及换热边界条件有关,还受到弹性变形应变率的影响,其在一定程度上改变物体内部的热量传递;k为热传导系数;ρ为质量密度;c为比热容;μ为泊松比;q为热流量;T0为结构初始温度.

1.3 热弹耦合下动力响应求解
对于文中热弹耦合动力学有限元方程求解的问题,采用联立求解式(1)和式(2),并相互交替迭代的计算方法,其中,运动方程式(1)则由Newmark法求解,热传导方程式(2)由Galerkin迭代格式进行求解.
对热传导方程式(2),取θ=2/3的无条件稳定迭代格式[14]如下:
(3)
而动力学方程式(1)则利用Newmark法将转化为求解如下的拟静力方程:
其中,γ是根据积分的精度和稳定性要求给定的可调参数.当γ=0.25时,积分格式无条件稳定[14].

2 区间参数热弹耦合响应分析
考虑到结构制造误差和外界环境等多种不确定性因素的影响,将结构的物性参数ρ、c、k、α、μ和E等均视为区间参数,同时,将结构所受外力f、温度载荷q以及结构初始温度T0亦视为区间参数,将它们统一以区间参数向量形式表示为β= (β1,β2,…,βm)T,β中既有区间结构参数也有区间载荷参数,其所在的范围为
(7)

将式(7)代入方程(1)和(2)中,则得描述区间参数梁结构的动力学和瞬态温度场方程如下:
由式(8)和式(9)可见,当结构参数和载荷均具有区间不确定性时,梁结构的时变位移响应u(β,t)和瞬态温度场T(β,t)将分别是两个区间参数时变函数的集合,即
u(β,t)和T(β,t)的上下界可表示为
以下将给出求解区间参数结构热弹耦合动力方程的响应上下界的计算方法.
3 热弹耦合区间结构有限元方程的求解方法
由于区间有限元方程的参数是区间变量,所有区间变量在各自的区间范围内的取值和变量的分布类型未知,对此问题为能够近似有效求解,可假设各变量在其区间范围内均服从具有最大熵的矩形分布[15].此假设的理由在于,将变量取到区间两端点的概率密度等同于取到其中值点的概率密度,从而将得到最为保守的计算结果,这对于结构的可靠性预测和设计结果是最为安全的.基于此假设,则可利用蒙特卡罗方法对每一区间变量在给定的区间内生成均匀分布的随机样本,进而再按照确定性有限元模型进行计算,最后得到结构响应的区间范围.

(1) 确定结构中独立的各区间变量及抽样次数l.
(3) 对于当前时间步长,随机抽取1~N之间的正整数并提取出其所对应子区间的两个端点值,记当前抽样次数i=1.(令f1和f2用来存储当前抽样所计算出来的最大和最小值,fmax和fmin用来存储当前时间步下的最大和最小值).
(4) 将各个参数子区间的端点值进行组合,代入式(3)和式(4),计算出函数值并比较.令当前计算结果中f1为最大值,f2为最小值,同时令fmax=f1,fmin=f2.
(5) 当i
(6) 结束循环抽样,输出当前时间步的最大与最小的响应fmax和fmin.
(7) 返回步骤(3),对下一时间迭代步进行新的抽样计算.
当在给定时间域上逐步计算完成之后,则得到整个时间域上动力响应的最大和最小包络线.
4 算 例
如图1所示的矩形截面悬臂深梁,长L=500 mm,宽b=100 mm,高h=50 mm,材料为铝,梁结构的区间参数分别为:ρ= [2 560,2 730] kg/m3,k= [190,210] W/(m·K),α= [20×10-6,23×10-6]/℃,μ= [0.31,0.35],q= [1.55×106,1.71×106] W/m2,c= [825,915] J/(kg·℃),E= [70×109,77×109] Pa,T0= [21,22]℃,f= [9,11] N/m2,其中梁上端面热流q作用的时间为 10 s.
求解悬臂梁热弹耦合动力响应分别采用两种有限元模型进行计算.图1为梁的动力学分析模型,沿其长度方向被离散为4个单元、5个节点,利用结构动力学方程计算得出节点的动力响应.图2为梁的热分析模型,沿梁横截面的厚度方向亦被离散为4个单元、5个节点,利用热传导有限元方程计算得出截面温差,从而计算出梁截面的热弯矩.
图3为梁自由端横截面中点温度场均值分别在耦合与非耦合(即耦合项H为0时,结构变形对温度场未产生影响)情况下的时间历程计算结果.从图3可以看出,耦合效应对横截面中点温度分布的影响,这是由于耦合与结构变形有关.由式(2)可知,由于耦合项的作用,温度场产生小幅度的波动.

图3 梁自由端中点温度的时间历程图4 梁自由端节点位移的时间历程
图4为梁自由端节点位移响应均值随时间变化历程的计算结果.在不考虑热弹耦合效应时,位移响应在各个周期的振动状态相同.而在考虑热弹耦合效应时,位移振幅随时间逐渐减弱,这种现象说明了耦合对振动产生的抑制作用.由阻尼的效应可知,这种减小的变化实际上相当于阻尼的作用.
图5给出了仅当E增大(取E=210×109Pa)以及E和α两者都增大(取E=210×109Pa 和α=60×10-6/℃) 的情况下,自由端节点位移均值响应的时间历程.由图5可见,E的增大使耦合效果明显,振幅衰减迅速.而当E和α都增大时,耦合效应不仅影响了振幅,还使得平衡位置发生了改变.说明了E和α对耦合的影响较大.该计算结果也可以通过热传导方程式(2)中的热弹耦合项的表达式进行分析.当参数E和α增大时,热弹耦合项就越大,其所表现的阻尼作用就越明显.

图5 E和α变化时梁自由端节点位移的时间历程图6 梁自由端节点位移响应区间的时间历程
图6给出了当梁各参数取区间变量时,利用区间有限元模型计算获得的自由端节点位移响应的区间时间历程.与确定性模型的计算方法相比,采用区间的计算方法可以得到更多的计算结果信息,不仅给出了结构位移响应的中值,亦可获得位移响应的区间范围.
以上算例均考虑了阶跃均布力f作用时的响应情况.为了考察该作用力对热弹耦合效应的影响,对无作用力和有作用力两种情况分别计算悬臂梁自由端位移响应均值,其计算结果见表1.从表1可见,当梁承受作用力时,变形比无承受作用力时的大,此时耦合效应的影响也更为明显.因此,当结构同时受到力和热载荷共同作用时,则需考虑耦合效应才能得到符合实际情况的计算结果.

表1 有无作用力时对悬臂梁自由端挠度的影响
5 结 论
研究了结构参数、力和热载荷同时具有区间不确定性时,梁结构在热弹耦合情况下的动力响应求解问题.通过悬臂梁算例,获得了以下结论:
(1) 在已知结构参数和载荷关于不确定性信息较少时,利用区间分析模型,并通过文中改进的蒙特卡罗数值仿真方法可以得到结构响应的区间范围.该方法无需不确定参数的概率信息,为解决区间参数梁结构的热弹耦合计算问题提供了一种途径.
(2) 在不考虑热与结构变形耦合的情况下,温度不受变形的影响.由于耦合效应,则结构变形对其温度场的分布产生影响,表现为温度的明显波动.
(3) 热弹耦合效应对结构位移振动有抑制作用,使结构的振幅随时间不断减小,并趋于稳态的平衡位置.
(4) 结构的弹性模量和热膨胀系数与耦合效应密切相关,两参数越大,热弹耦合效应越明显.
(5) 在有力的作用时,不考虑热弹耦合效应对结构位移的影响将可能造成一定的计算误差.因此,在高精度要求的结构分析和设计中,考虑热弹耦合效应的影响是十分必要的.
[1] Thornton E A, Kim Y A. Thermally Induced Bending Vibrations of a Flexible Rolled-up Solar Array[J]. Journal of Spacecraft and Rockets, 1993, 30(4): 438-448.
[2] Lee Y S, Jeon B H, Kang H W. Free Vibration Characteristics of Thermally Loaded Rectangular Plates[J]. Key Engineering Materials, 2011, 478(81): 81-86.
[3] 赵寿根, 王静涛, 黎康, 等. 考虑辐射散热叠层板热诱发振动的有限元分析[J]. 力学学报, 2010, 42(5): 978-982.
Zhao Shougen, Wang Jingtao, Li Kang, et al. Finite Element Method Analysis of Thermally Induced Vibration of Laminated Plates Considering Radiation[J]. Chinese Journal of Theoretical and Applied Mechanics, 2010, 42(5): 978-982.
[4] 范绪箕. 高速飞行器热结构分析与应用[M]. 北京: 国防工业出版社, 2008.
[5] Boly B A. Thermally Induced Vibrations of Beams[J]. Journal of the Aeroautical Science, 1956, 23(2): 179-181.
[6] Babaei M H, Abbasi M, Eslami M R. Coupled Thermoelasticity of Functionally Graded Beams[J]. Journal of Thermal Stresses, 2008, 31(8): 680-697.
[7] 李智勇, 刘锦阳, 洪嘉振. 作平面运动的二维平面板的热耦合动力学问题[J]. 动力学与控制学报, 2006, 4(2): 114-121.
Li Zhiyong, Liu Jinyang, Hong Jiazhen. Coupled Thermoelastic Dynamics of a Two-dimensional Plate Undergoing Planar Motion[J]. Journal of Dynamics and Control, 2006, 4(2): 114-121.
[8] Manoach E, Ribeiro P. Coupled, Thermoelastic, Large Amplitude Vibrations of Timoshenko Beams[J]. International Journal of Mechanical Sciences, 2004, 46(11): 1589-1606.
[9] 薛明德, 向志海. 大型空间结构的热-动力学耦合问题及其有限元分析[J]. 固体力学学报, 2011, 32(s1): 318-328.
Xue Mingde, Xiang Zhihai. Thermal-dynamic Coupling Problem of Large Space Structures and Its FEM Analysis[J]. Chinese Journal of Solid Mechanics, 2011, 32(s1): 318-328.
[10] 阎彬, 陈建军, 马洪波. 随机弹性杆在随机瞬态温度场下的热响应分析[J]. 电子科技大学学报, 2012, 41(4): 631-636.
Yan Bin, Chen Jianjun, Ma Hongbo. Thermal Response Analysis of Stochastic Pole Structures under Random Transient Temperature Field[J]. Journal of University of Electronic Science and Technology of China, 2012, 41(4): 631-636.
[11] 王敏娟, 陈建军, 林立广, 等. 区间参数智能梁结构闭环系统动态特性分析[J]. 电子科技大学学报, 2011, 40(1): 152-156.
Wang Minjuan, Chen Jianjun, Lin Liguang, et al. Dynamic Characteristic Analysis of Closed Loop Systemsfor the Intelligent Beam with Interval Parameters[J]. Journal of University of Electronic Science and Technology of China, 2011, 40(1): 152-156.
[12] 梁震涛, 陈建军, 朱增青, 等. 不确定结构动力区间分析方法研究[J]. 应用力学学报, 2008, 25(1): 46-50.
Liang Zhentao, Chen Jianjun, Zhu Zengqing, et al. Dynamic Interval Analysis for Uncertain Structures[J]. Chinese Journal of Applied Mechanics, 2008, 25(1): 46-50.
[13] Marakala N, Kadoli R. Thermally Induced Vibration of a Simply Supported Beam Using Finite Element Method[J]. International Journal of Engineering Science, 2010, 2(12): 7874-7879.
[14] 王勖成. 有限单元法[M]. 北京: 清华大学出版社, 2003.
[15] 易平. 对区间不确定性问题的可靠性度量的探讨[J]. 计算力学学报, 2006, 23(2): 152-156.
Yi Ping. Discussions on Reliability Measure for Problems with Bounded-but-unknown Uncertainties[J]. Chinese Journal of Computational Mechanics, 2006, 23(2): 152-156.
