混合遗传算法在舰空导弹武器系统火力分配中的应用＊

朱传伟 童幼堂 董受全

（海军大连舰艇学院 大连 116018）

1 引言

遗传算法是一种借鉴生物界的进化规律演化而来的随机化搜索方法，其从试图解释自然系统中生物的复杂适应过程入手，模拟生物进化的机制来构造人工系统的模型［1］。由于遗传算法具有高度的并行处理能力、强鲁棒性和全局搜索能力，被广泛应用于诸多领域，包括可以用于舰空导弹武器系统火力分配。由于传统遗传算法在实践应用中存在着一定的局限性。因此，采用混合遗传算法对舰空导弹武器系统的火力分配问题进行研究，既能克服传统遗传算法的不足，又能保证传统遗传算法的效率。

2 火力分配模型

舰空导弹武器系统火力分配模型是依据各空袭目标的威胁程度及其飞行参数，确定应由哪部照射雷达对其实施照射，保证最大数量的目标满足射击条件，使总体作战效能最大［2］。

设有N个来袭目标，所有照射雷达都分配目标。则火力分配问题就是使下面的期望函数值最大化。

式中：Rj为目标j的威胁系数；Xij为布尔值，用来判断目标j是不是分配给了照射雷达i。如果目标j分配给了照射雷达i，则Xij＝1，否则Xij＝0。

式（2）表示一次分配给目标j的照射雷达数量不超过bj个，式（3）表示每部照射雷达最多能照射一个目标。

在现代海战场上，只有当目标进入到舰空导弹武器系统发射区，同时目标处于照射雷达作用范围以内时，照射雷达才能照射目标［3］。因此，当照射雷达照射目标时，通常要受到舰指挥员决策、杀伤区大小、照射雷达实际作用范围、照射雷达的转移时间等因素制约。

2.1 舰指挥员决策约束条件

由于作战情况的复杂多变，获得的数据信息不可能非常完全、确定和可靠，舰指挥员的判断、决策、选择仍然是十分必要的，即舰指挥员应对火力分配方案有一定的干预能力［4］。通过赋予各目标对应的威胁系数Rj值，在火力分配中加权，体现出舰指挥员决策对火力分配结果的影响。

2.2 照射雷达有效作用范围约束条件

对于照射雷达Zr来说，其有效作用范围是舰空导弹武器系统杀伤区与照射雷达Zr的实际作用范围的共同区域。设第一个目标到达照射器雷达Zr的有效作用范围远界的时间为TY（Zr，1），到达其有效作用范围近界的时间为TY（Zr，1）＋TD（Zr，1），TD（Zr，1）为第一个目标在其有效作用范围内停留的时间。该照射雷达对第一个目标的开始照射时刻为TL（Zr，1），只有满足约束式（4）时，该照射雷达才能有效照射第一个目标。

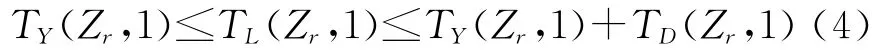
照射雷达Zr执行完前一个目标的照射任务后，在向后一个目标开始执行照射任务之前需要有一段转移的时间。设该照射雷达的最小转移时间为TZ。

同理可以得出，只有同时满足约束式（5）和式（6）时，该照射雷达才能有效照射第二个目标。

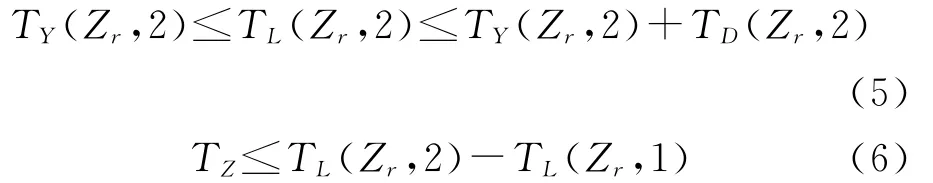
式中：TY（Zr，2）为第二个目标到达该照射雷达有效作用范围远界的时间；TD（Zr，2）为第二个目标在该照射雷达有效作用范围内停留的时间；TL（Zr，2）为该照射雷达对第二个目标的开始照射时刻。

3 基于自适应惩罚函数法的混合遗传算法

3.1 适应度评价函数设计

以上的火力分配模型属于约束优化问题，而用遗传算法不能直接去求解约束优化问题，需要做一些处理。通常是通过引入惩罚函数，将有约束优化问题转换为无约束优化问题，再使用遗传算法求解。但在实际计算中，惩罚函数法中的惩罚因子通常难以合理选取，如果惩罚因子过小，惩罚项得不到足够的惩罚，满足约束条件的精度就会降低；反之，惩罚函数会增大，造成对期望函数分配的权重过小，忽略了对期望函数的影响，得到的往往是局部最优解，同时也给计算增加困难。

为了较好地解决惩罚因子的确定问题，采用了文献［5］中的自适应惩罚函数方法，将惩罚因子选取为关于自变量Xij的函数。同时，为了加快收敛速度，借鉴了“多级惩罚”的思想，即对违反约束大的段给予较大惩罚，而违反约束小的段给予较小的惩罚。

则适应度评价函数为

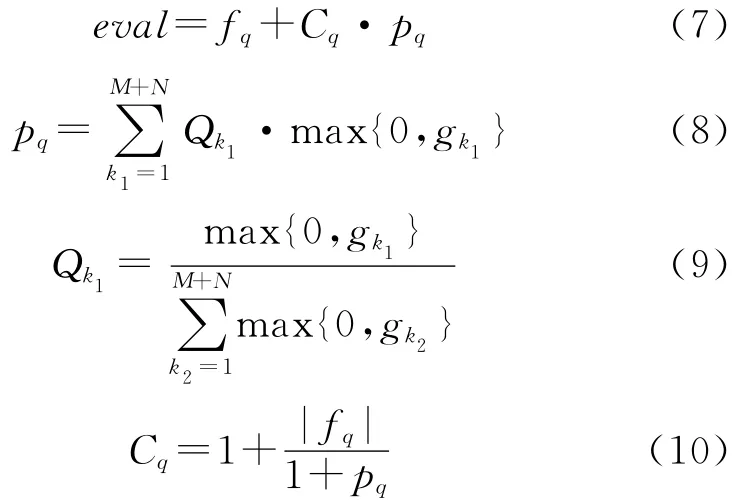
式中：pq为惩罚函数；Cq为惩罚函数的系数。其具有“多级惩罚”的功能，并且在算法的迭代过程中起到了“自适应”调节的作用。

3.2 混合遗传算法设计

舰空导弹武器系统的混合遗传算法的结构构成见图1，其主要操作流程是首先使用遗传算法，当满足终止条件时，完成全局搜索，输出群体适应度最优个体。然后通过使用爬山法，继续完成局部搜索过程，最终得出适应度最优个体。

3.2.1 遗传算法设计

1）编码体制的选择

染色体采用二进制编码方式，设个体的串长为M×N，为第h（h≥1）代染色体kh串，表示第i部照射雷达对第j个目标的火力分配情况，则染色体表示为…＝（…）。

2）初始群体设定

传统遗传算法是按随机方法产生一组初始解群体，但其中的每个染色体不一定满足约束条件式（2）和式（3），以下方法可使初始解群体自动满足这两个式子，其步骤为

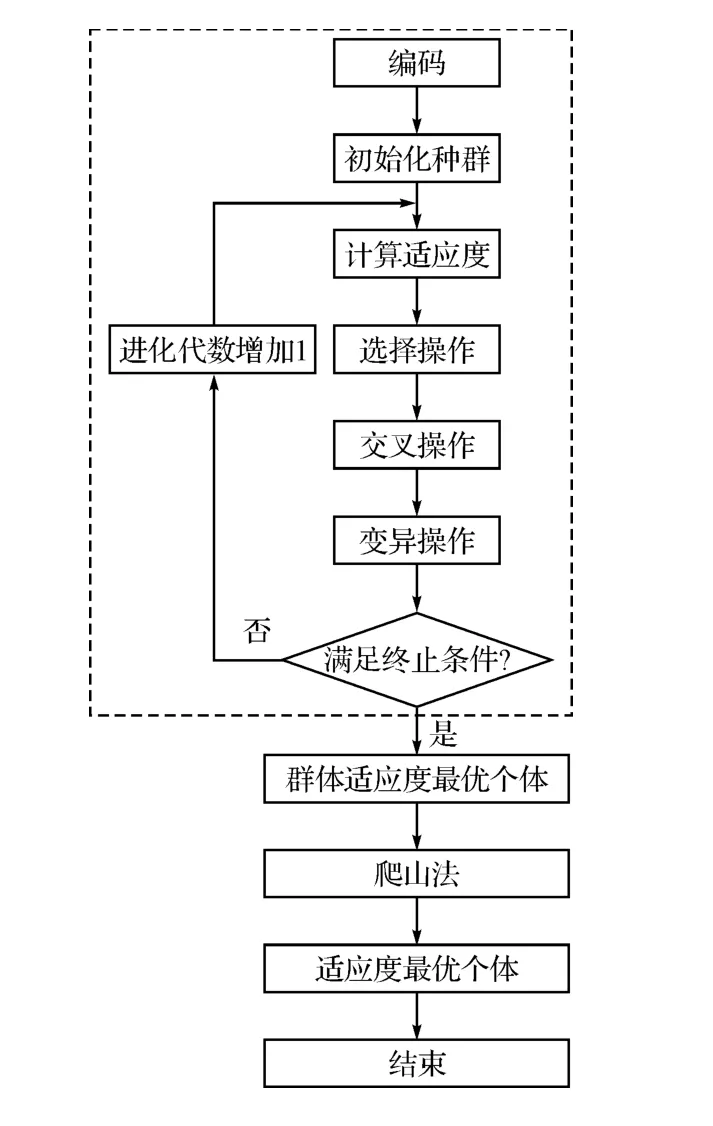
图1 混合遗传算法构成示意图

第一步：将所有染色体中每个基因座均赋值为0；

第二步：对于每一个染色体，将其变换为M×N阶矩阵。随机选择其中的一个或两个基因座，根据式（3）在每一行中置一个1。然后随机选择其中的几个基因座，使第j列中最多置bj个1，以满足式（2）。

3）个体适应度评价

由于单个个体代表一种火力分配方案，必须将火力分配方案通过照射雷达有效作用范围约束条件的检验，形成可行的火力分配方案，然后根据式（7）计算个体适应度值。

照射雷达有效作用范围约束条件的检验方法为：仍以照射雷达Zr为例进行说明。根据照射雷达Zr的有效作用范围，将先进入有效作用范围的目标作为该照射雷达第一次照射的目标，将稍后进入有效作用范围的目标作为该照射雷达第二次照射的目标，即依据进入有效作用范围的先后顺序来确定该照射雷达的照射目标次序。当目标同时进入有效作用范围时，优先照射目标威胁系数值大的目标。

对于照射雷达Zr的第一次照射，依据式（4）判断该照射雷达是否可有效照射第一个目标，如果不能有效照射第一个目标，则染色体中该照射雷达照射第一个目标对应的布尔值赋值为0。同时，当该照射雷达还有照射其它目标的性质时，依据上述方法选择另外一个目标作为第一个目标，依上述程序进行判断。如能有效照射第一个目标，则需判断该照射雷达是否还要照射第二个目标。如还要照射第二个目标，则依据式（5）和式（6）进行判断，经过判断后，如不能有效照射第二个目标，则染色体中该照射雷达照射第二个目标对应的布尔值赋值为0。同时，当该照射雷达还要照射其它目标时，依据上述方法选择另外一个目标作为第二个目标，依上述程序进行判断。如能有效照射第二个目标，则需判断该照射雷达是否还要照射第三个目标。如此反复，直到火力分配方案满足该照射雷达有效作用范围约束条件时为止。

4）选择操作

选择时在群体中选择生命力强的个体产生新的群体的过程。在传统遗传算法中，常根据个体的适应度大小采用“赌轮选择”策略。该策略虽然简单，但容易引起“早熟收敛”和“搜索迟钝”问题。为了避免这一问题，采用比例选择和精华模型相结合的选择策略，将每个代群种He个个体中适应值最大的一个直接进入下一代。下一代种群中其它个体将由上一代种群中剩余的He－1个个体，用轮盘赌法产生。这样一方面可以保证种群中最优个体可以生存到下一代；另一方面，又避免了个体间因适应值不同而被选入下一代的机会太悬殊，从一定程度上保证了种群的多样性。

5）交叉操作

交叉是指对相互配对的染色体按某种方式相互交换其部分基因，从而形成两个新的个体［6］。传统遗传算法对父染色体之间进行交叉操作时，是随机选取的，未考虑它们各自适应度的大小。因此，交叉操作存在着很大的盲目性，影响了算法的性能。

由于在生物界中，很多生物种群是以一个个小群体生活于自然界的。这些生物种群的下一代均依靠最优秀的个体和其它母体产生，如蜜蜂、狼群等。根据这些生物现象，采取的交叉过程如下：一是选择适应度最大的个体为最优个体，其直接进入到下一代，设为第h代染色体kh1（其表示为…）；二是随机选择与最优个体kh1配对的一个个体，设为染色体kh2（其表示为…）；三是将与互换与互换，与互换，依此形成两个新的个体。当这两个新个体的适应度不相同时，去掉其中适应度最小的个体，保留另外一个个体。否则，任意保留其中一个。

6）变异操作

变异运算是指将个体染色体编码串中某些基因座上的基因值用该基因座的其它等位基因来替换，从而形成一个新的个体［7］。对于第h代染色体kh，随机选择其中的与，将两者互换，形成新的染色体与。d1，d2，e1，e2＝1，2，…，M。然后评价新产生个体的适应度值，将其与父代个体进行比较，若适应度值相同，则视为无效变异操作，去除这个新产生的个体，重新按以上方法实施变异操作；否则，则视为有效变异操作，新产生的个体取代父代个体。

7）自适应交叉率和变异率

交叉概率pc和变异概率pm对遗传算法性能具有重要影响，不少文献对此进行了系统研究。其中，相关文献［8］将pc、pm与群体的收敛性、个体的适应值相联系，自适应地改变交叉概率pc和变异概率pm值的大小，将进化过程分为渐进和突变两个不同阶段：渐进阶段强交叉，弱变异，强化优势型选择算子；突变阶段弱交叉，强变异，弱化优势型选择算子。具体公式为

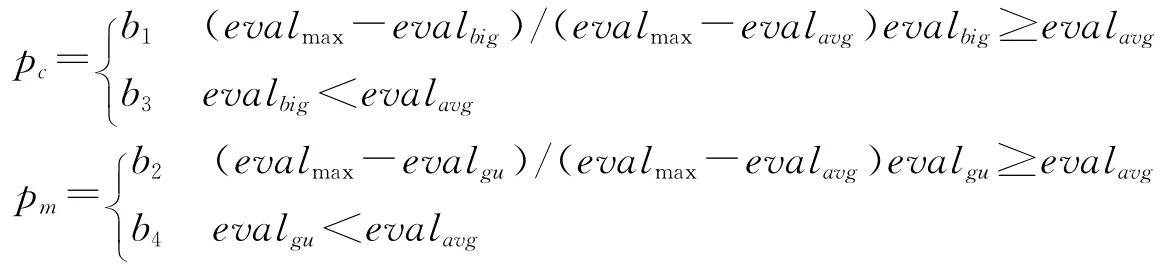
式中：evalgu为第g（g＝1，2，…，H）个个体的适应度值；evalbig为两个交叉个体的适应度最大值；evalmax为当前群体的适应度最大值；evalavg为当前群体的适应度均值。

通常取b1＝b3＝1.0，b2＝b4＝0.5。

8）算法终止条件

判断是否达到了所设定的世代数，或者两世代的平均适应度评价函数值之差的绝对值是否小于给定的阈值εh。εh为一个小的正数，但也不能太小，否则爬山法局部寻优发挥的作用不大。如果不满足终止条件，则进化代数h＝h＋1；否则，则输出当前群体适应度最优个体，遗传算法部分结束。

3.2.2 爬山法设计

爬山法是一种简单的启发式搜索算法［9］。它将最陡上升方向作为搜索方向，能够以最快的速度爬到山顶。其搜索过程概况是：扩展当前节点。并估价它的子节点，将最优子节点作为下一步扩展节点，依此类推，直到爬到“山顶”为止。爬山法搜索速度快，容易达到局部最优［10］。

由于染色体采用二进制编码方式，那么采用位爬山法时要根据位变异的方式和概率等不同，具有多种具体样式。对于位变异方式，要采用从左向右的顺序一次变异。对于以上遗传算法实施全局搜索后得出的单一最优个体ky来说，其串长为M×N，则位爬山法的搜索过程如下：

步骤1：取序号dp＝1；

步骤2：以一定的概率pdj变异最优个体ky的第dp位基因值，即将基因值取反，由0变到1，或由1变到0，得出新个体kx；

步骤3：按照以上的“个体适应度评价”方法，计算新个体kx的适应度evalx和最优个体ky的适应度evaly；

步骤4：比较新个体的适应度。当evalx＞evaly时，新个体kx取代最优个体ky；否则，不变。同时dp＝dp＋1，返回到步骤2。如此不断循环，直到当dp＝M×N时，循环结束，得出适应度最优个体。

4 结语

基于混合遗传算法求解的舰空导弹武器系统火力分配问题能够为解决防空作战运筹领域类似的问题提供了一种新的思路。由于传统遗传算法在实践应用中，会出现早熟现象、局部寻优能力较差等不足，而爬山法具有较强的局部寻优能力［11］。因此，可以将遗传算法的把握总体能力和爬山法的局部搜索能力相互结合，取长补短，构建混合遗传算法，从而可有效避免陷入局部极值并最终趋向全局优化。

［1］马亚龙，邵秋峰，孙明.评估理论和方法及其军事应用［M］.北京：国防工业出版社，2013：164－174.

［2］任少伟，贺正洪，刘进忙.基于改进遗传算法的防空火力优化分配方法［J］.火力与指挥控制，2004，29（3）：82－84.

［3］陶英歌，郭乃林，罗红英.基于遗传算法的目标分配优化模型研究［J］.系统工程与电子技术，2003，25（7）：817－819.

［4］张海峰，吴富初，王光源.防空系统目标威胁评估与火力分配模型［J］.火力与指挥控制，2004，29（6）：29－31.

［5］刘琼荪，周声华.基于自适应惩罚函数法的混合遗传算法［J］.重庆大学学报，2006，29（6）：78－81.

［6］曳永芳，杜永清，行小帅.一种抑制早熟收敛的改进遗传算法［J］.山西师范大学学报，2010，24（2）：24－28.

［7］程杰，任伟，徐军凯.遗传算法在导弹火力分配中的应用［J］.现代防御技术，2008，36（4）：93－96.

［8］M.Srinivas，L.M.Patnaik.Adaptive probabilities of crossover of crossover and mutation in genetic algorithms［J］.IEEE Trans.Systems，Man Cybernet，1994，24（4）：656－667.

［9］隋树元，王树山.终点效应学［M］.北京：国防工业出版社，2007：53－65.

［10］钱进，叶寒竹.基于作战过程的机动导弹武器系统生存能力评估建模［J］.装备指挥技术学院学报，2007，18（4）：116－123.

［11］王书齐，沈治河.基于可变模糊集决策理论的航空母舰编队防空决策方法研究［M］.北京：海潮出版社，2013：130－134.