邻信道合并的改进及其测频方法

曾德国，陈望杰，倪小康，周贵良

（中国航天科工集团8511研究所，江苏 南京 210007）

0 引言

在信道化接收机体制中，宽带雷达信号经常会出现跨通道的情况，对信道编码器及脉内均有较大的影响，可以考虑采用非均匀信道化来处理。数字下变频［1］、几乎完全重构［2］、基于信号重构理论的动态信道化［3］都能实现非均匀信道化，但分别存在计算量太大、综合滤波器系数设计较为困难、信号重建较为复杂等问题。1995年，Lee等提出了邻信道合并（ACM）的概念，指出通过设计信道化中的原型滤波器，就可以使得相邻信道仅通过加法就能无失真地恢复相邻信道的幅频响应［4］。2010年，杨君［5］等在 ACM 的基础上，对无失真条件进行了加强，认为要幅频响应与相频响应均无失真才能符合要求；提出了先设计和信道响应、然后反推子信道响应的方法来设计ACM，效果良好但计算较为繁琐。

ACM只需要对子信道进行相加即可得到和信道，计算非常方便。本文对文献［5］所提的方法进行了改进，给出了一种原形低通滤波器解析式，以直接设计子信道响应，并对其和信道响应进行了证明。另外，以宽带信号为例，采用仿真证明了本文设计的ACM的正确性，并考虑了窄带情况下的一种比幅测频法。

1 简化的ACM设计及ACM的特性

1.1 简化的ACM

根据文献［5］所述，对于一个含2D个子信道的信道化接收机，要使相邻子信道直接相加的和信道能没有频率、相位失真且具有良好的频率选择性，则信道化的低通原型h0（n）的频响H0（ejω）应满足：

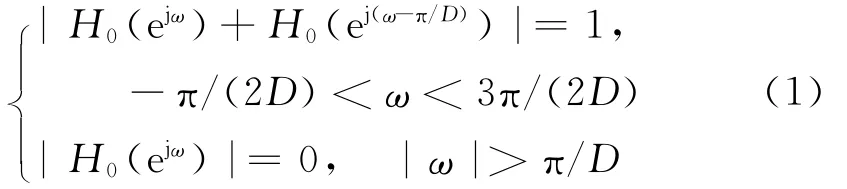
杨君提出，可以先设计和信道幅频响应｜H0（ejω）＋H0（ej（ω－π/D））｜，使其满足（1）式，然后再反推出H0（ejω）。该方法增强了先设计H0（ejω）、然后再验证｜H0（ejω）＋H0（ej（ω－π/D））｜的目的性，可操作性较好。并提出了两种设计｜H0（ejω）＋H0（ej（ω－π/D））｜的方法：插值法和求极限法，且得出了极限法中，将｜H0（ejω）＋H0（ej（ω－π/D））｜的中心频率变到零频后的和响应为a（n）的一个表达式为：

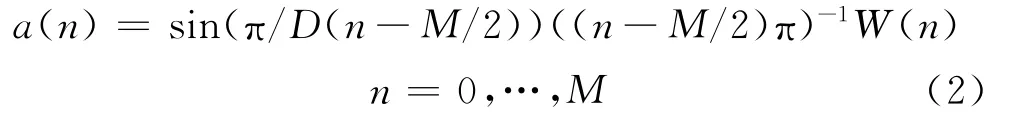
式中，M取为2D的偶数倍，W（n）为窗函数。通过对a（n）按照文献［5］的方法求极限，即可得到h0（n）。

下面证明，将h0（n）取类似a（n）的形式，就可直接得到所需的低通原型。由于h0（n）的带宽为a（n）的一半，故令：

则第k个信道的冲击响应为：

第k个及第k＋1个信道的和冲击响应a′（n）为：

令M＝2p×2D，p为整数，化简得：

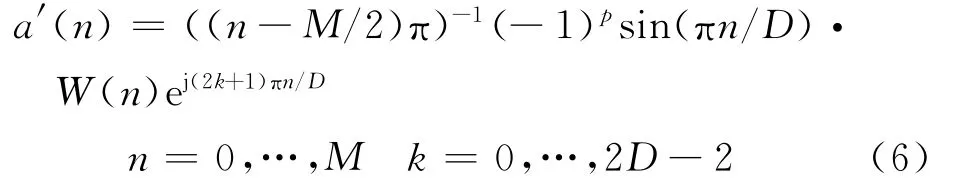
将（2）式中的a（n）化简后可得：

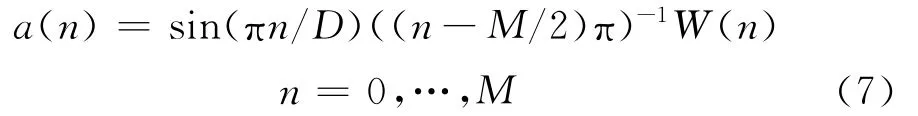
综合（6）式与（7）式可得：

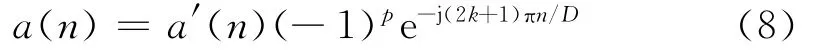
从（8）式中可以看出，两个信道的和响应a′（n）下变频（2k＋1）π/D后，乘以一个与M有关的非零常数，即可得到期望的和响应a（n）。由于非零常数不影响响应，因此，a′（n）是一个中心频率为（2k＋1）π/D的带通滤波器，滤波器的性能与式设计的一致。在此，只证明了两个邻信道相加得到的响应与设计的响应一致，也可证明，多个邻信道相加得到的响应也与期望的响应是一致的。综上所述，当低通原型采用（3）式时，可保证期望的和信道的响应等于两个子信道的响应之和，而无需先设计（2）式的和信道响应去按照极限法反推子信道响应。

1.2 ACM 的特性

假设实信道数为256，采样率2.56GSPS，则2D＝256，取p＝2，则M＝1024，采用布莱克曼窗时，窗函数、（3）式对应的原型低通滤波器及邻近信道的和信道的频率响应如图1所示。其中，第一个实信道分布于－0.5～0.5的频率单元、第二个信道分布于0.5～1.5的频率单元。可见，首先，原型滤波器由于频率卷积效应较窗函数扩展了谱宽，进而带来旁瓣的下降（－58.1dB下降到－76.9dB）；其次，在常规滤波器的设计中，频率单元为1处原型滤波器应该截止，然而，ACM在此处是处于过渡带，要到1.25左右才能完全截止；再次，对于常规原型滤波器，在0.5以内应该是平坦的，然而，此处的原型滤波器在0.5附近约有6dB的衰减，此处也是邻信道的交界处；最后，对于和信道，合并后的低频部分保持了原型滤波器的特性，高频部分保持了第二个信道的特性，和信道中间部分增益几乎恒为1，即不会有不平坦。综上所述，按照（3）式设计的ACM具有过渡带宽宽及可合并两个主要特性。

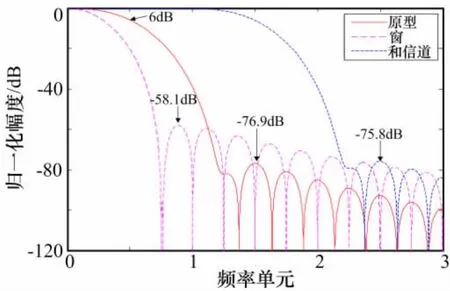
图1 低通原型及和信道的频率响应

1.3 ACM使用策略

由上文可知，ACM具有过渡带宽宽及可合并两个主要特性。按照传统的信道化设计观点，过渡带宽宽也就等价于通带内被衰减及阻带内抑制度不够，这将导致双音动态所需的频率间隔较大，这是一个相对于传统接收机的劣势。可合并是传统信道化设计所不具有的一个新特点，图2给出了信道合并前后的频响，从中可以看出合并后通带变宽，且在通带内很平坦，这是相对于传统接收机的一个优势。从图2还可以看出，ACM合并前后分别可以得到两种频率响应，而两种不同的频率响应具有不同的功能，这也就使得ACM在使用时有不同的策略。

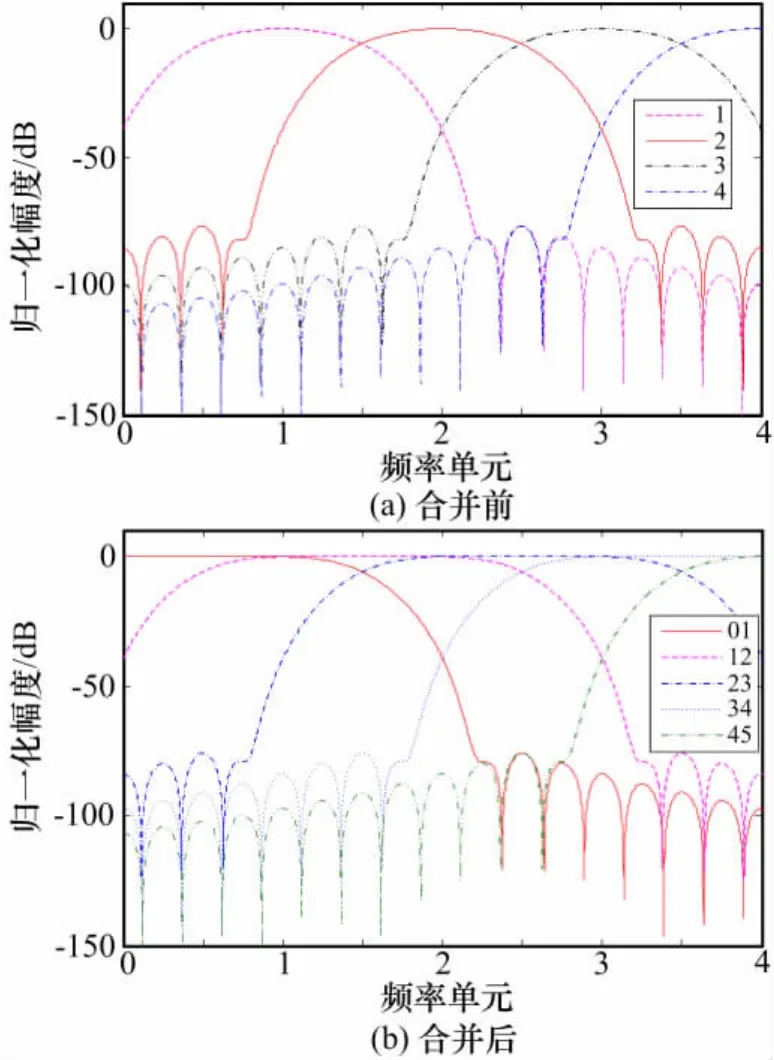
图2 合并前后比较

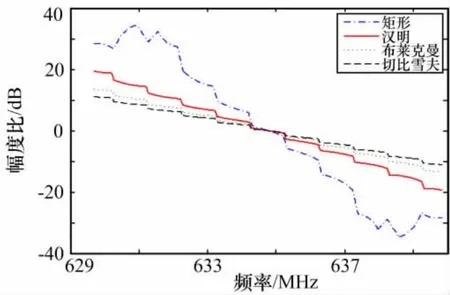
图3 幅度比与输入频率的关系

对于图2（a）的响应，由于其频率抑制度不够，当任意一个信号落入两个频率单元之间时，两个滤波器一般都会有较大的输出，且两个输出的幅度之比代表了输入信号频率的位置。因此，可以采用比幅法来测量输入信号的频率，原理与比幅测向类似。图3给出了使用不同窗函数时，不同输入频率与幅度之比的关系，其中，比幅时，每个信道的幅度取为该信道输出作FFT后的最大幅度。可见，子信道带宽越宽（采用切比雪夫窗），则幅度的波动范围越小。另外，汉明、布莱克曼及切比雪夫窗对应的频率与幅度比都是单调的，即频率与幅度比是一一映射，理论上可以根据幅度比确定频率；然而，对于矩形窗，幅度比非单调，幅度比与频率非一一映射，即给定一个幅度比，不能唯一确定信号的频率，因此，不能用其来进行频率估计。

对于图2（b）中合并后的响应，因为不存在合并前在交界处的不平坦，所以可以用来重构跨道的宽带信号。一种具体的方法为将相邻的合并前有信号的信道直接相加，即可重构宽带信号。这种方法认为如果相邻的两个道都有信号，则是属于一个宽带信号。当然，也可进一步对两个相邻信道都有信号时进行处理，以区分其是宽带信号还是多个相邻的窄带信号，具体方法可以参考文献［6］的14～15章。

2 仿真分析

从两个方面来衡量ACM的性能：宽带信号的重构能力以及窄带情况下的频率估计性能。

2.1 宽带信号重构能力

首先，考察合并后宽带信号的重构能力。采样率为2.6GSPS，实信道个数为256，抽取率为16，窗函数分别为矩形、汉明、布莱克曼及切比雪夫窗。假设输入信号为400MHz带宽的LFM，参考盲分离的信号恢复标准，以相似系数为评价标准，定义为：

式中，s（n）为输入信号，sr（n）为恢复信号。

图4给出了重构效果，从中可得出两点结论。首先，根据ACM设计的不同窗滤波器在信道数足够大时可以高保真（相似系数收敛至1）地恢复输入信号，而未根据ACM设计的常规原型低通滤波器，由于合并后其幅频一致性不能满足式，所以其相似系数不能收敛到1；另外，当采用不同的窗时，相似系数的性能也不一样，在实验的各种窗中，性能从优到劣排序依次为：切比雪夫、布莱克曼、汉明及矩形，这刚好与窗的抑制度保持一致：抑制度越好，则相关系数越高，但该差异不是很明显。综上所述，在实际设计ACM时，应尽量选择具有较好抑制度的窗。

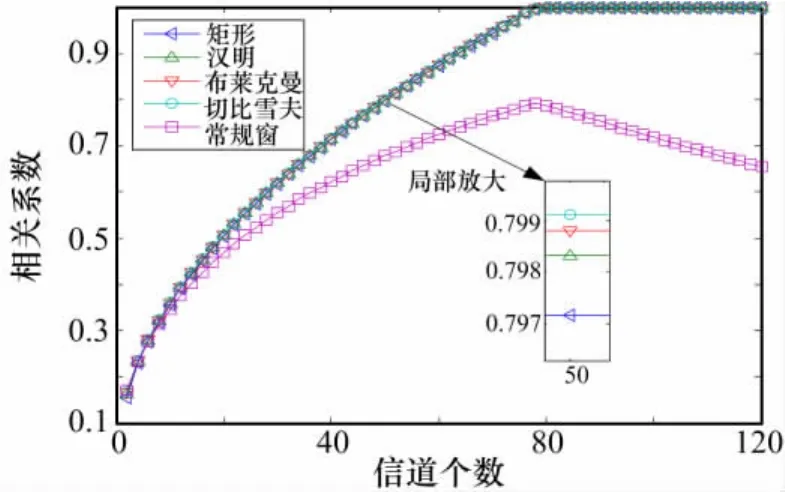
4 相似系数与恢复信号时采用的信道个数的关系

2.2 比幅法测频性能

在采样率为2.6GSPS，脉宽为1μs的条件下考察比幅法的测频性能。输入频率是在第63信道的中心频率到第64信道的中心频率之间，按照均匀分布随机选取200个频率。信噪比（SNR）范围为－20～0dB，步进2dB。图5给出了测频性能与不同窗及SNR的关系，并与Rife法及CRLB进行了比较，可以得出两点结论。首先，高信噪比条件下（信道化前－14dB，对应信道化后约为7dB），比幅法精度最高的是切比雪夫及布莱克曼窗，其精度稍微好于Rife法；汉明窗性能较Rife稍差；矩形窗频率估计误差较大。其次，比幅法较Rife法降低了测频的灵敏度（约为2dB）。切比雪夫、布莱克曼、汉明、Rife性能都与CRLB较为接近。可见，比幅法可以作为窄带测频的一种备选方法。

图5 不同窗在不同SNR条件下的测频性能

3 结束语

本文从ACM的和信道设计方法出发，提出了一种直接设计ACM低通原型滤波器的解析方法，理论推导及仿真都证明了该方法的正确性。另外，以相似系数为评判标准，用仿真证明了ACM可高保真地恢复输入的宽带信号。最后，给出了基于比幅的窄带信号测频方法，其性能较佳。需要指出的是，在比幅测频时，可以采用合并后与合并前的比幅，以进一步减少信道化的灵敏度损失。

［1］Harris FJ，Dick C，Rice M.Digital receivers and transmitters using polyphase filter banks for wireless communications［J］.IEEE Trans.Microwave Theory and Techniques，2003，51（4）：1395－1412.

［2］李冰，郑瑾，葛临东.基于NPR调制滤波器组的动态信道化滤波［J］.电子学报，2007，35（6）：1178－1182.

［3］朱晓，司锡才.一种高效动态数字信道化方法［J］.哈尔滨工业大学学报，2009，41（7）：160－164.

［4］Lee JJ，Lee BG.A design of nonuniform cosine modulated filter banks［J］.IEEE Trans.On Circuits and Systems II－Analog and Digital Signal Proc.，1995，42（11）：732－737.

［5］杨君，袁嗣杰，吕镜清.ACM信道化滤波器设计中的陷波问题分析研究［J］.宇航学报，2010，31（12）：2764－2770.

［6］Tsui J.Special design topics in digital wideband receivers［M］.Norwood，MA：Artech House，2010.