基于Copula理论的商业银行集团客户信贷风险研究

刘 澄，田 岚,2，张静波

（1.北京科技大学 东凌经济管理学院，北京 100083；2.河北经贸大学 金融学院，河北 石家庄 056001）

基于Copula理论的商业银行集团客户信贷风险研究

刘 澄1，田 岚1,2，张静波1

（1.北京科技大学 东凌经济管理学院，北京 100083；2.河北经贸大学 金融学院，河北 石家庄 056001）

对新巴塞尔协议下的信用风险管理模型：KMV模型、CreditRisk+模型和CreditMetrics模型进行简单介绍并分析其优劣之处。结合中国商业银行的实际情况，选择CreditMetrics模型建立商业银行信用风险管理体系；并运用Copula函数理论对CreditMetrics模型进行了修正，建立了信贷风险评估体系；在matlab中编程实现修正后的模型，且进行了仿真模拟实验。

商业银行；集团客户；信用风险管理；Copula理论

一、引言

目前，我国不少企业已经走上了集团化的道路，商业集团客户授信业务随之迅速发展。但是中国各商业银行对于集团客户的信贷风险管理情况总的来说并不理想。一是集团客户有更复杂的组织机构，分布于不同行业和地区，财务报表的可操作性过大以及制度突破能力更强；二是商业银行在激烈的市场竞争中，会采取放开授信政策等方式争取集团客户，容易产生信贷风险；三是面临着社会信用体系和监管的缺失等外部问题。因此，研究一套基于客观数据的、能够输出具体指标的信用风险管理体系对于我国商业银行具有重要的现实意义。

本文通过对新巴塞尔协议下较为常用的信用风险管理模型，包括KMV模型、Credit Risk+模型和CreditMetrics模型进行介绍和比较，结合我国商业银行的实际情况，选择较为适合的模型建立信用风险管理体系，并运用Copula函数理论对模型进行改进，建立信贷风险评估体系，最后进行仿真模拟。

二、信用风险管理模型的选取

（一）信用风险管理模型比较分析

通过比较KMV模型[1]、Credit Risk+模型[2]和CreditMetrics模型[3]，可以发现CreditMetrics模型具有以下优势：该模型根据历史的评级信息来进行统计分析；是盯市模型，考虑了违约和不违约两种状态，以及信用等级的升降或转移引起的价差风险；该模型是离散估值模型；采用现金流折现法，对合同的现金流进行折现；属于无条件模型，反映有限的借款者或信用项目的信息，而条件模型更要综合考虑。

（二）我国商业银行信用风险管理模型适用性分析

为了解几种模型在我国金融市场条件下的适用性，再从模型的研究对象、输入与输出变量及适用条件来对模型进行比较，如表1所示。

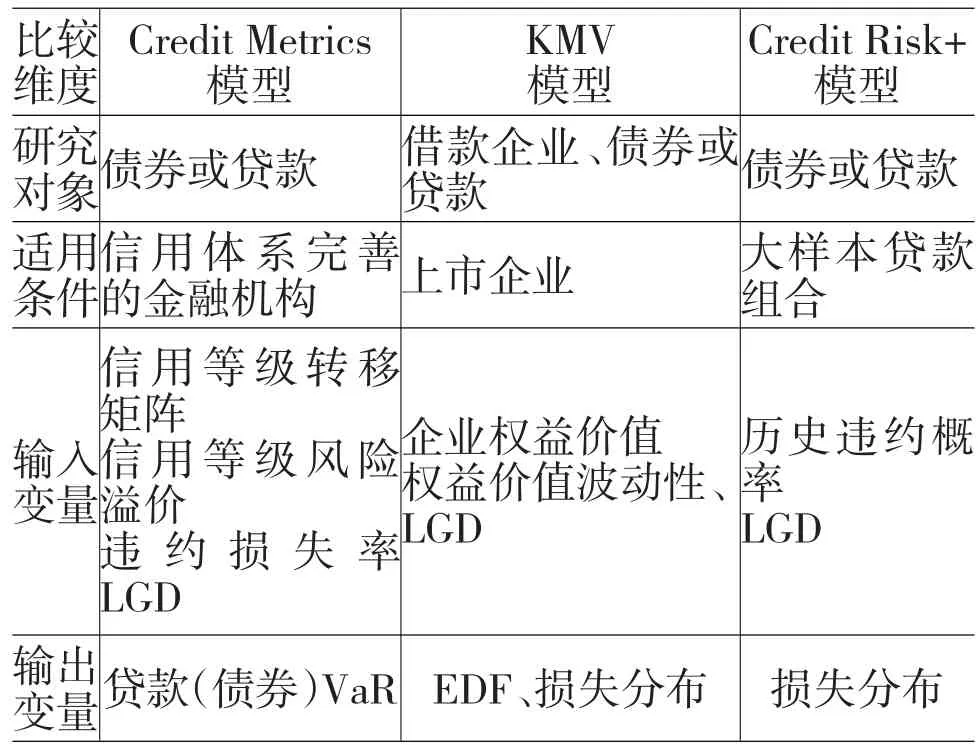
表1 模型输入输出参数比较

通过分析，可以初步认为CreditMetrics模型是较为适合现阶段我国商业银行的信用风险管理模型。一是我国大部分商业银行都开发了自己的内部评级体系，信用评估体系已初具规模。二是目前一些银行在积极开发“内部评级法”系统，并按照巴塞尔新资本协议的初级要求，正全面启动内部评级工程。三是债券市场的发展为CreditMetrics模型的输入参数提供了数据基础。总之，我国目前的金融市场发展程度比较低，在我国商业银行信用风险管理的过程中使用KMV和CreditRisk+模型，条件基础还很薄弱。因此，本文将采用CreditMetrics模型建立我国商业银行集团客户的信贷风险评估体系。

三、集团客户信贷风险评估体系设计

（一）Creditmetrics模型的改进

CreditMetrics模型中，影响信贷资产价值的包括违约事件和信贷质量的变化。模型采取盯市的概念来计算信用风险价值，构造了一个模拟信贷资产所有潜在变化以及违约波动的组合计算框架。框架包括三个关键环节如图1。（1）风险暴露金额。（2）由信用变化导致的单个敞口价值波动。（3）不同信贷资产价值变化的相关性。对于该模型的改进主要有两个方面：一是数据方面的改进，针对我国实际情况对CreditMetrics需要的数据，如信用转移概率矩阵，违约回收率，远期收益率等进行调整。二是计算方法上的改进，主要针对贷款组合中贷款间相关系数计算的改进。在缺乏成熟市场统计数据的前提下，增强模型的可操作性。

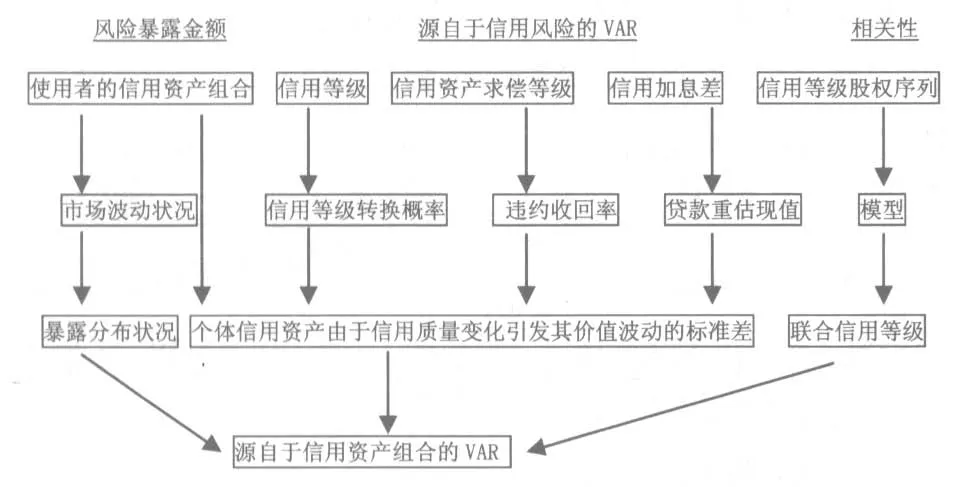
图1 CreditMetrics模型基本框架

（二）信用风险评估体系的建立

1.信用转移矩阵调整

信用转移概率矩阵可根据评级机构对企业的信用评级历史数据进行计算，本文选取标准普尔1981—2009年全球公司信用转移矩阵。

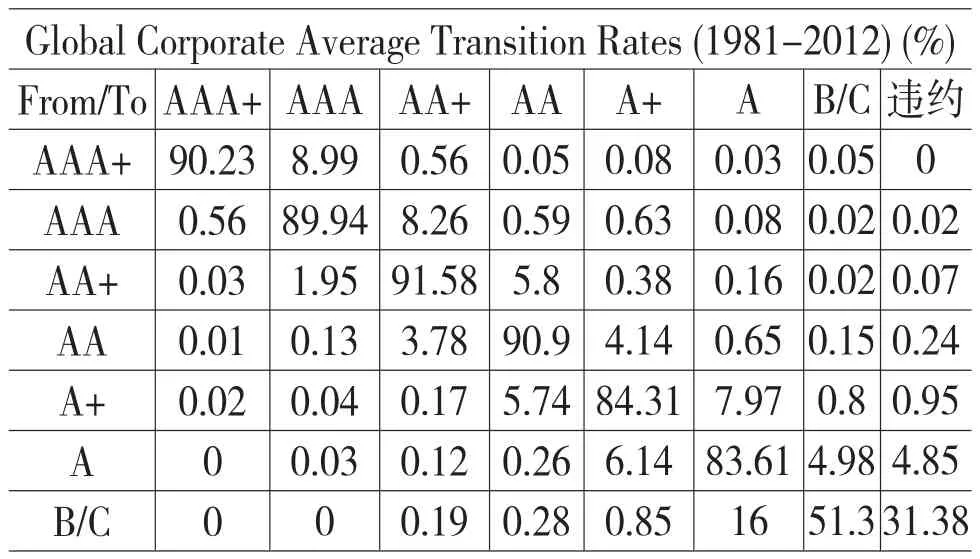
表2 调整后的信用转移概率

为了方便下文实证部分计算，同时与信用利差期限结构的评级划分标准保持一致，将我国商业银行评级中的B、C同归于标准普尔公司的CCC/C级别中。这主要因为信用利差期限结构在我国的研究尚处于起步阶段，数据不易获得，本文采用基于美国公司债券市场得到的信用利差期限结构。调整后的信用转移矩阵如表2。

2.远期收益率曲线的确定

远期收益率一般选择一种无风险收益率作为投资的依据，本文选择银行间国债收益率代替。因为银行间国债利率是一种市场化的风险极低或者无风险的利率，我国商业银行的资金允许买卖国债，排除中间业务和贷款，购买国债可视为风险最低的投资。我国有专门的机构公布银行间国债利率，数据较易获得。选取2013年4月12日中国银行间国债收益率作为基准利率，根据公式(1+X1)(1+ri)i=(1+Xi+1)i+1推导出远期收益率。

表3 银行间国债远期收益率(%)

我国商业银行对贷款的定价采取的是基于基准利率的上浮调整，这一方法没有精确的参照标准，数据难以获得。为了确定银行贷款的期末价值，可将银行向某一企业发放贷款的情景视为银行购买某企业发行的收益率为贷款利率。

信用加息差的数据通过中债信息网——收益率曲线获得。其中，AAA+(2)为无合格担保企业债。

远期收益率加上各个级别的信用风险溢价则可确定各个级别的远期零利率曲线，如表4。

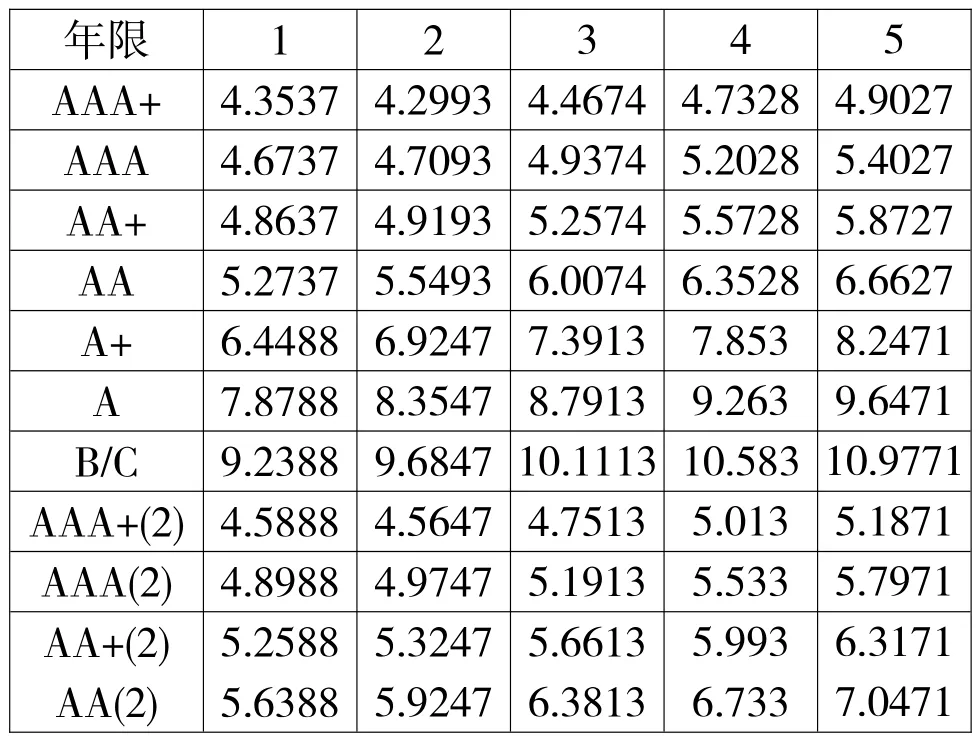
表4 远期零利率曲线（%）

3.违约损失率确定

本文采用的违约损失率来自中国农业银行2011年经济资本计量方案。如表5。

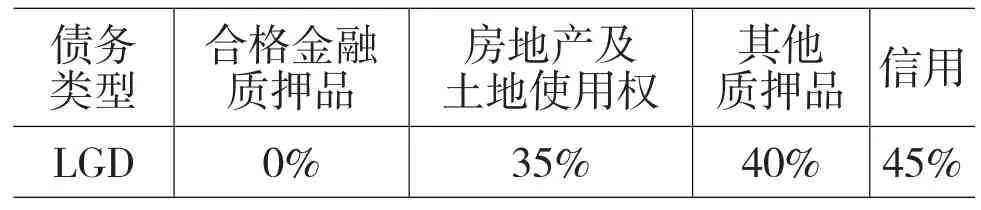
表5 违约损失率

4.相关性估计

由于某些宏观因素，贷款评级之间的变化存在一定的相关性，某一项贷款评级的变化可能会影响到其他贷款的评级，进而影响整个组合的VaR值。这也是CreditMetrics模型实证研究的主要缺陷。相关实证研究中普遍采用的是经验相关系数，一般为同行业0.5，不同行业0.3。显然这样的计算方法不能精确反映单笔贷款之间信用变化的相关性。

本文采用Copula函数来刻画各项贷款之间信用变化的相关性，通过对能反映企业信用状况变化指标进行拟合，选取合适的Copula函数求得联合概率分布，求得贷款间的相关系数。本文采用企业所在行业指数的相关性模拟企业信用变化的相关性。

5.计算资产组合VaR

计算资产组合的VaR的关键是联合信用转移矩阵的求解，CreditMetrics中，该部分的求解是借鉴莫顿模型来进行的。

公司资产价值由股权价格来代替，根据莫顿模型，可表示为

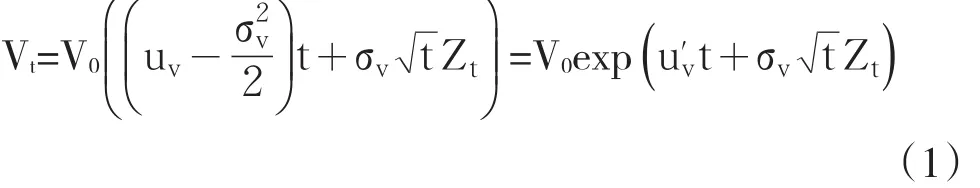
uv是公司资产价值瞬时收益率，是其方差，Zt～N（0，1）。Vt一为个违约的门槛值，资产价值和Vt之间的差决定了发债企业的信用等级。

为求不同阈值水平的资产价值，即P(Vt≤vi)转换为：

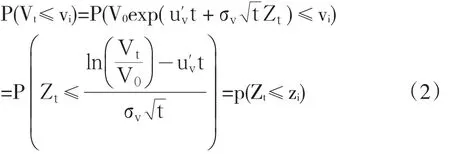
这样根据概率求正态分布的反函数，可以得出对应阈值。

CreditMetrics选择股票价格作为公司资产价值的替代变量来推导公司之间的违约相关系数，进而推导联合转移概率与违约概率。

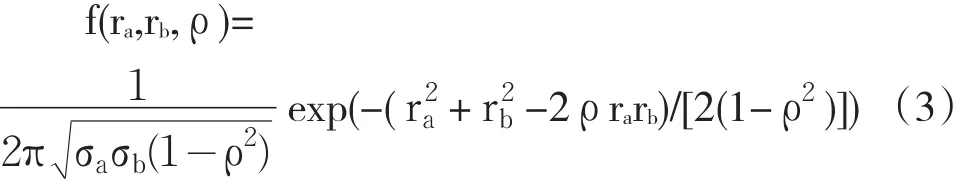
债务人的联合分布概率则只要求下列积分：

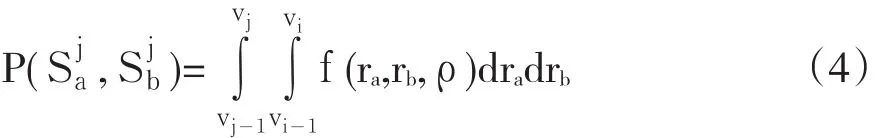
进一步，将两种债券的期末可能价格结合起来，可以计算出上述两类资产联合价值，结合得到的联合信用转移概率矩阵就可求得组合的均值与标准差，进而求得不同置信度的VaR值。

本文实证部分在matlab下编程实现，在求得变量的边缘分布即两组受益率数据单独的概率分布后，可直接调用ksdensity(X，P，function，icdf)函数返回特定累积概率下的样本值，这样就不受限于收益率服从正态分布的限制，再根据H(x,y)=C(F(x),G(y))求得其联合分布概率。在进行多维数据相关性分析时，比CreditMtrics模型使用莫顿模型更加简便。

下面本文使用两组资产收益率数据进行实证分析，多维数据可直接加以推广。

四、仿真模拟研究

现有某医药集团旗下两家企业各有一笔贷款额度都为100万元，期限均为5年，企业a初始评级为AAA，贷款类型为房地产担保贷款，贷款利率为6%；企业b初始评级为AA，贷款类型为信用贷款，贷款利率为7%。下面计算这个贷款组合的VaR。

首先来分析企业a和企业b的相关性。这里采用目前较为流行的以股票价格波动代表公司价值变动进而模拟公司信用状态的变化。从大智慧股票分析软件中获取2005年1月4日至2013年5月10日企业a与企业b的股票价格，对其进行相关性分析。

（一）基于Copola函数的相关性估计

第一步是边缘分布的确定。

通过收益率频率直方图，得到AAA级贷款收益率的偏度与峰度分别为0.0899和4.3372，AA级贷款收益率的偏度和峰度分别为0.0164和4.8988。初步可以看出两变量分布近似对称且具有一定的尖峰厚尾特性。再对两组收益率数据进行Kolmogorov-Smirnov(K-S)检验、Jarque-Bera检验、Lilliefors检验。三种检验的h值均为1，P值均小于0.01，其中JB检验和L检验的P值过小，在matlab中返回0.001。可见两组收益率数据均不满足正态分布，而是服从某种近似对称的尖峰厚尾分布。下面采用非参数估计的方法确定两组收益率数据的分布。

在matlab中调用ecdf函数求样本的经验分布函数，同时调用ksdensity函数用核密度估计的方法估计样本的分布。

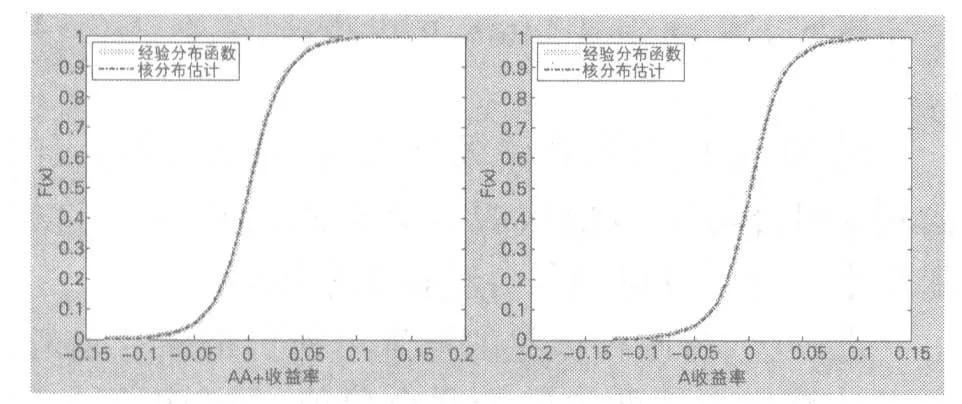
图2 收益率的经验分布函数与核分布估计图

可以看出两组样本的经验分布函数与核分布估计函数几乎完全重合。由此，采用核分布估计确定两组样本的边缘分布函数。

第二步，选取适当的Copula函数。

在确定样本的边缘分布函数即U=F(x)，V=G(y)之后，就可以根据(Ui,Vi)(i=1,2,…,n)的二元直方图形状选取适当的Copula函数。

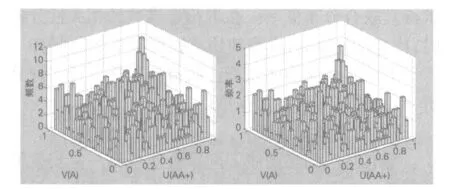
图3 二元频数和二元频率直方图

Copula函数有不同的种类，依据二元直方图和各Copula函数的分布特征，初步选定正态Copula、t-Copula和Clayton Copula来描述原始数据的相关结构。

用各个Copula函数的Kendall秩相关系数、Spearman秩相关系数与原始数据求得的Kendall秩相关系数、Spearman秩相关系数作对比，发现t-Copula较好地反映了两组收益率之间的秩相关性。

比较各个Copula函数在样本点处的分布函数值与经验Copula函数在样本点处的分布函数值平方欧式距离，得出t-Copula函数的值最小。

综合考虑，t-Copula模型能更好地拟合日收益率样本数据。根据最后确定的Copula函数的形式及参数，估计收益率的相关系数，进而得到企业a及企业b的信用变化的线性相关系数为：ρ=0.1182。

所以最后选用的t-Copula函数为：

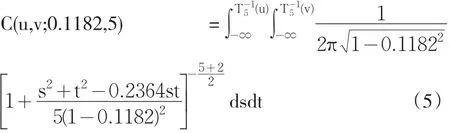
其中μ,v是拟合得到的边缘分布函数。所得到的t-Copula函数的概率密度函数和分布函数如图4。

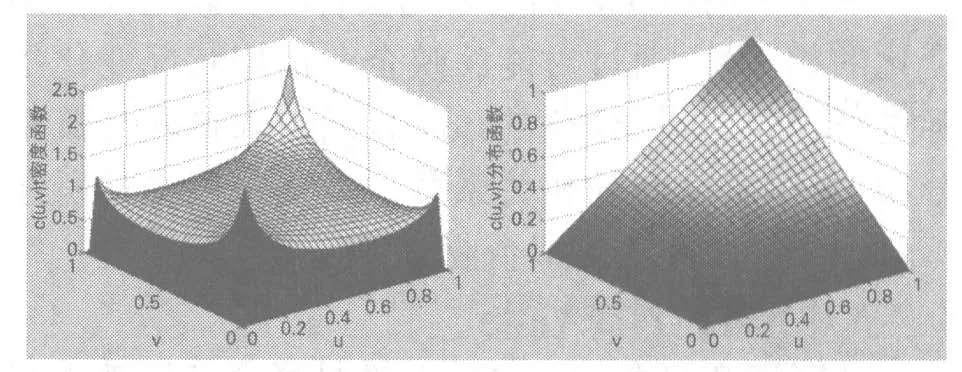
图4 t-Copula函数的概率密度函数和分布函数

（二）信贷组合VaR计算

根据上文研究得到的信用转移矩阵、远期零利率曲线及违约损失率，可计算得到企业a与企业b不同信用级别下的年末债务价值，见表6。

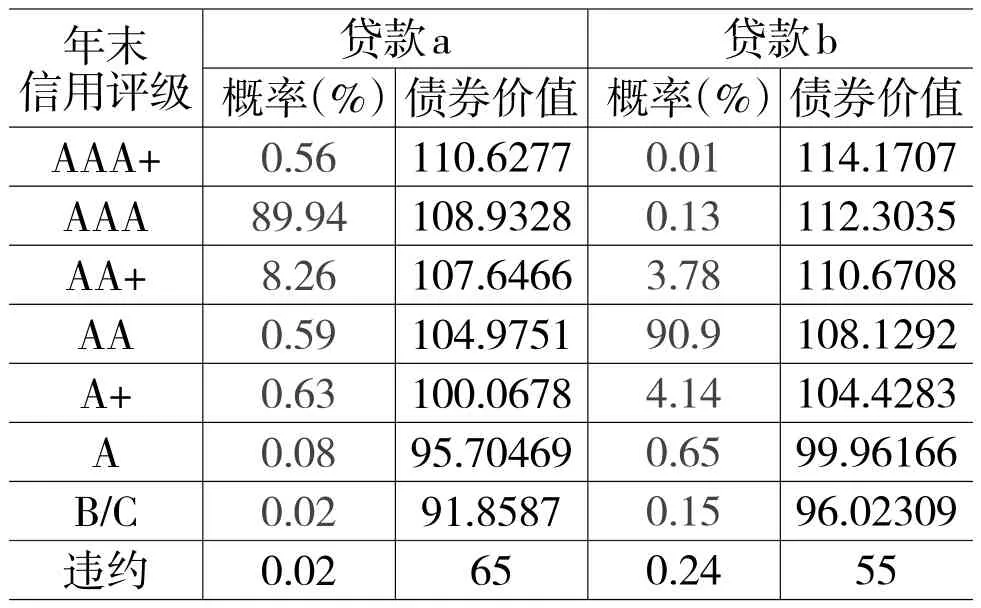
表6 年末债务价值分布

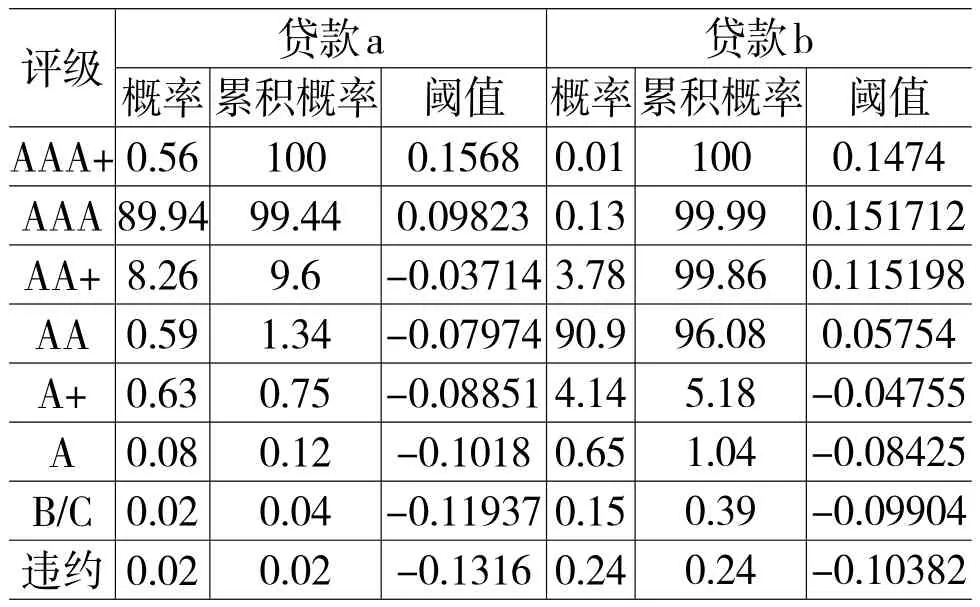
表7 各信用等级阈值

计算贷款a的期末价值期望为μa=108.843，同理μb=107.8793。贷款a期末价值方差为=1.297，标准差σa=1.138839，同理=8.203，标准差σb= 2.864097。可根据上文拟合得到的核分布函数来确定不同累积概率下的阈值，结果见表7。

根据前面得到的Copula函数，在matlab中调用copulacdf函数结合牛顿莱布尼兹公式，得到联合信用转移概率矩阵，结果如表8。

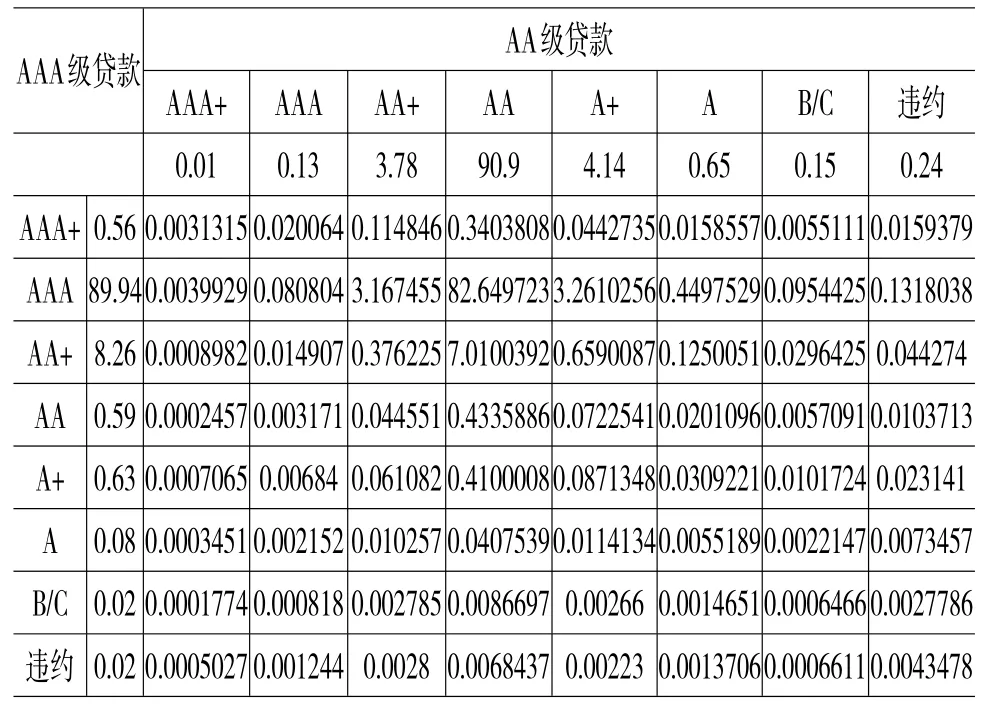
表8 联合信用转移矩阵

将两笔贷款的年末可能价格与联合信用转移矩阵结合起来，就可以计算出上述两类资产联合价值分布共有64种可能，如表9所示。

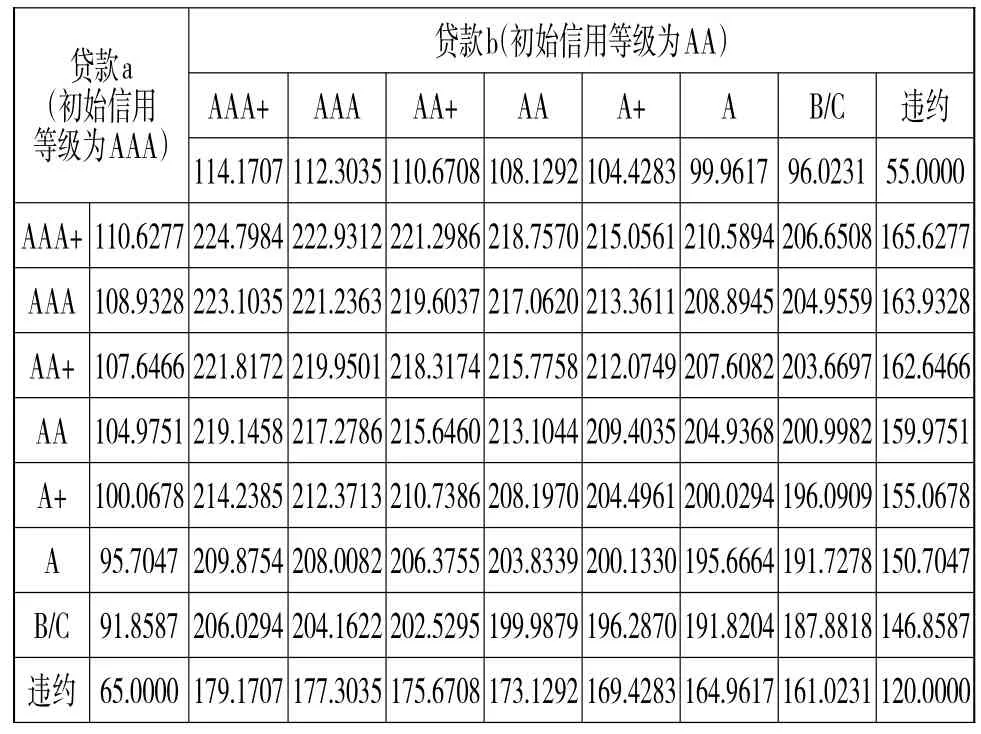
表9 贷款组合联合价值分布

结合联合信用转移概率分布与年末贷款组合价值分布，计算组合的均值M和标准差σ分别为：

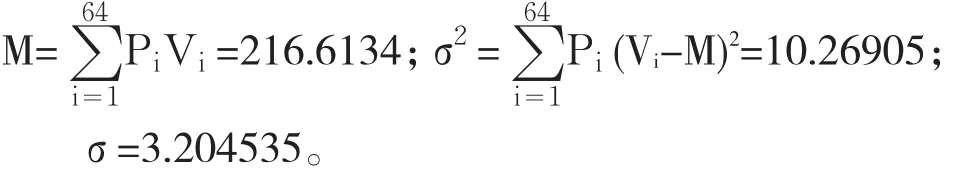
在正态分布下，该贷款组合的信用风险估值为：99%置信度的VaR=2.335*3.204535=7.48259万元；95%置信度的VaR=1.645*18.2191=5.271461万元。即该贷款组合有1%可能性损失超过7.48259万元，有5%可能想损失超过5.271461万元。

如果用标准差衡量风险，贷款a的标准差是1.138839，组合的标准差是3.204535，则贷款b引致的边际风险为2.065696，小于贷款b的单独标准差2.864097，这就是分散化效应。

在更多维的资产组合VaR计算方面，由于Copula函数多维数据相关性分析的优越特性，将两组收益率数据的二维向量直接扩展到多组收益率数据的多维向量即可。

（三）结果分析

计算贷款组合的VaR时，如采用目前多数研究中使用的同行业0.5，不同行业0.25-0.35之间的经验相关系数，只有当两组样本中都包含数量足够多项的资产时才有意义，且从以深圳证券交易所的行业指数替代资产价值进行相关性分析的结果来看，经验相关系数与实际求得的行业相关系数差距很大，与实际情况有较大出入。实际应用中带来的问题就是，如VaR的估值过高，商业银行针对这一贷款组合，采取更为保守的管理措施，提取更高的拨备，或降低授信额度，如此可能导致银行盈利能力的减弱；如VaR的估值过低，容易导致的结果就是商业银行过度授信，其经营风险被放大。

从商业银行集团客户信贷风险评估的实际来看，引入Copula函数后的CreditMetrics模型，能更有针对性地分析单项贷款间的相关性，进而求得贷款组合VaR，也就是对整个集团的信贷风险进行了评估，具有较强的精度和较高的操作性，商业银行可根据VaR方便地调整对该集团客户的拨备和授信额度。

五、结语

本文使用基于样本数据得到的Copula函数本身直接求解联合信用转移矩阵，消除传统方法中对资产价值服从正态分布的限制，经验证此方法可行有效，并且在计算机编程实现的情况下比传统方法更加简便，具有更大的实用价值。

[1]Crosbie,Peter J.Modeling DefaultRisk,Manuscript[Z].KMVCorporation.1999.

[2]Credit Suisse.Credit Risk+:A Credit Risk Management Framework[Z].Credit Suisse Financial Products.1997.

[3]JPMorgan.CreditMetrics TechnicalDocument [Z].1997.

（责任编辑：王淑云）

1003-4625（2014）08-0061-05

F832.33

A

2014-06-04

刘澄（1967-），男，辽宁辽阳人，教授，博士后，博士生导师，北京科技大学东凌经济管理学院金融工程系主任，研究方向：金融工程；田岚（1985-），女，河北邢台人，北京科技大学东凌经济管理学院博士研究生，河北经贸大学金融学院讲师，研究方向：风险管理；张静波（1989-），男，河南周口人，硕士研究生，研究方向：资本市场。