基于改进的灰色模型烟草产品销量的预测分析

张敏珏，帅小应，江保利

（1.池州学院 数学与计算机科学系，安徽 池州247000；2.池州市烟草公司，安徽 池州 247000）

基于改进的灰色模型烟草产品销量的预测分析

张敏珏1，帅小应1，江保利2

（1.池州学院 数学与计算机科学系，安徽 池州247000；2.池州市烟草公司，安徽 池州 247000）

针对非平滑序列短期预测精确度不高的问题，文章采用指数函数-对数函数变换法对数据列进行灰色预测分析，并从理论上证明此法对获取精准预测结果的优越性。最后，借助池州市烟草公司2007年1月——2012年1月黄山(金皖烟)硬盒同期数据，对其下一年同期销售量进行预测分析并与传统灰色预测模型相比较，进一步验证改进的灰色模型的有效性及优越性。

灰色预测；销售量；指数函数-对数函数变换法

1 引言

近些年来，烟草行业在全面推广和大力推进“按销量组织货源”的形势下，如何准确地预测市场需求，为企业的经营提供真实有效的理论依据显得尤为重要。然而在以往的预测过程中，特别是地市级烟草公司的销量预测过程中，由于受到了决策者工作经验、职业素质以及同期原始数据偏少等方面的限制，销量预测值很难准确地把握好。鉴于此，我们将采用灰色预测理论帮助我们解决问题。灰色预测理论是我国著名学者邓聚龙教授于(1982年)[1]创立的。其主要内容是通过构建灰色模型来解决预测问题，但前提条件是要求原始数据列为光滑离散函数。而大多数情况下，我们所处理的数据为非光滑离散函数列，这就需要在构建灰色模型之前，首先对原始数据进行某种处理以改善其光滑性。陈捷涛（1990年)[3]提出欲使预测结果越精准，关键在于提高原始数据的光滑性。为了保证灰色模型能够获得好的预测效果，众多学者为原始数据提供各种变换方法，以增强其光滑特性，并由此得到一些改进的灰色预测模型。如，陈捷涛（1990年)[3]提出了对原始数据进行对数变换并证明该变换可以提高原始数据列的光滑性；李群（1993年）[4]提出了数据幂函数变换和对数函数—幂函数变换法且证明这两种方法均可提高原始数据列的光滑度；王建根（1996年）[5]对对数变换、幂函数变换、对数函数-幂函数变换在提高原始数据序列光滑性的效果差异情况进行了系统的讨论，并证明出对数函数-幂函数变换的效果最好；吕林正（2001年）[6]通过对原始数据进行上下移动变换，有效地提高了模型的拟合精度；何斌（2002年）[7]提出对原始离散数据列进行指数变换，并从理论上证明了此法较对数变换和幂函数变换法更有效；张军（2008年）[8]提出了含参线性函数变换法、含参对数函数-线性函数变换法和含参线性函数-对数函数变换法等等。但将指数函数-对数函数变换法运用到改进数据列光滑性并不多见。本文从理论上证明指数函数-对数函数变换法可以有效改进原始数据列的光滑性，并通过应用改进后的灰色模型，以安徽省烟草公司池州市分公司进销存综合数据为例，对企业下一年同期数据进行预测分析以此验证该改进模型的有效性和优越性。

2 构建改进的灰色模型

2.1 原始数据预处理

运用灰色预测理论对数据进行建模之前，必须对序列中的数据进行预处理，从而产生新的数列，以此来挖掘和寻求数的规律性。对于数据序列的预处理，我们给出如下步骤：

（1）采用函数变换法改进非平滑原始数据序列的光滑性

很明显，根据引理2和推论2，指数函数-对数函数变换法较对数函数-幂函数变换法的效果更好,通过这种变换方法可以大大提高预测精度。

（3）一次累加序列的生成

2.2 改进的GM（1,1）的建立

设y(0)为原始数据x(0)进行指数函数-对数函数变换后的光滑数列，其中

并称Y为数据向量，B为数据矩阵，u为参数向量，GM(1,1)则模型可以表示为矩阵方程Y=Bu。根据最小二乘法可以求得参数估计量为：

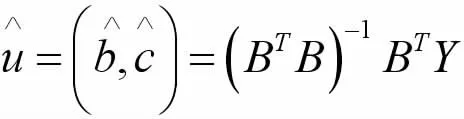
2.3 灰色预测

由上节的（2）式，（3）式，我们可以得到数据列y(0)的预测值为

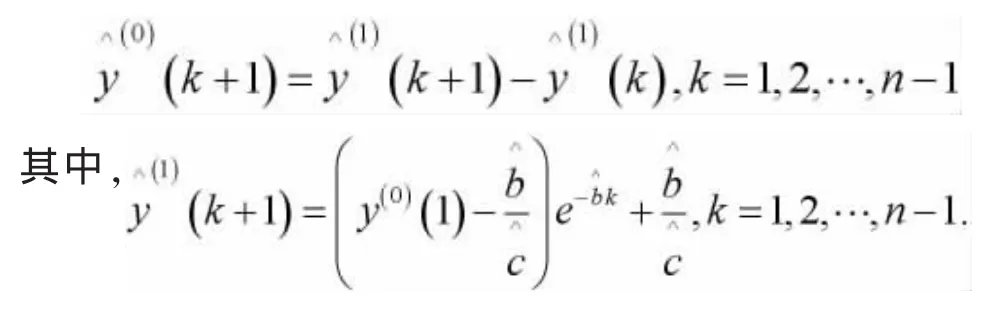
我们通过GM(1,1)得到数据列y(0)的预测值后，需要对这些预测值的效果进行检验，在实际分析过程中，我们主要运用以下两种方法对这些预测值进行检验：

（1）残差检验：令残差为 ε(k)，计算

如果ε(k)<0.2则可认为达到一般要求；进一步地，若ε(k)<0.1则认为达到较高的要求。

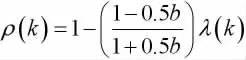
如果ρ(k)<0.2则可认为达到一般要求；进一步地，若ρ(k)<0.1则认为达到较高的要求。

对于达到检验要求的y(0)的预测值，我们可以通过还原，即得原始数据的预测值。

3 实证预测分析

针对安徽省烟草公司池州市分公司进销存综合数据，以第一类香烟（批发价200元/条以上）中的黄山 (金皖烟)硬盒为例，根据2007年1月至2012年1月月同期销售量，通过构建改进模型GM(1,1)，我们预测出2013年1月黄山(金皖烟)硬盒的月销售量，并与实际数据相对比，以此验证改进后的灰色预测模型的有效性及优越性。

3.1 实证分析步骤

（1）数据的检验与处理

根据烟草进销存综合数据表，该种商品销量的原始数据

由（1）式我们发现，并不是所有的级比都包含在相应可容覆盖（0.75148,1.28403）中，这里，我们采用指数函数-对数函数变换法提高原始数据列x(0)的光滑性，此处令 a=1.41，其级比结果为 λ=[1.2788,1.2283,1.0973,1.1732,1.1159]，很明显，各级比值均包含在可容覆盖(0.75148,1.28403)内。

（2）建立GM(1,1)模型并对原始数据进行拟合，预测分析

这一部分，我们主要是通过MATLAB软件来完成，其编写程序如下：

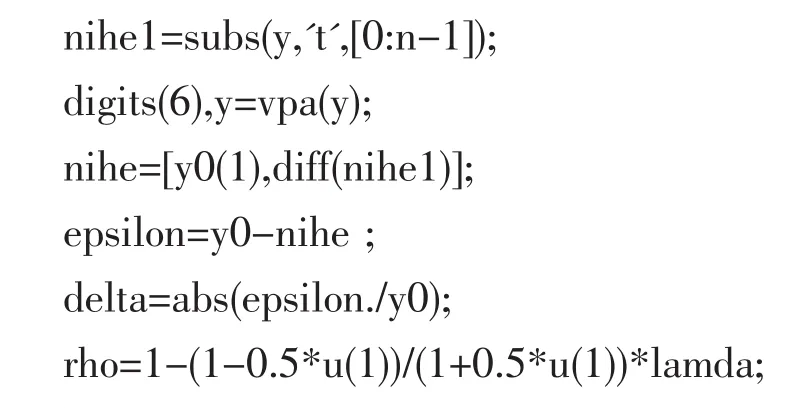
3.2 实证分析结果

由计算机随机模拟所得实验结果如下：

（1）原始数据x(0)的拟合值

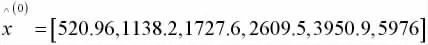
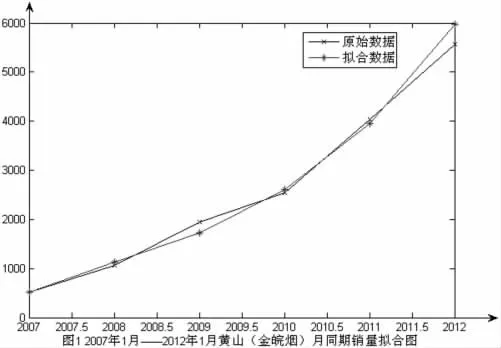
图1 2007年1月-2012年1月黄山（金皖烟）月同期销量拟合图

（2）拟合值检验

表1 拟合值检验表

根据表1，我们发现上述各检验系数值均小于0.1，可以认为该模型达到较好的要求。

（3）预测值的对比

为了验证改进的灰色预测模型在数据处理中的优越性，我们将其与传统的灰色预测模型作一比较。借助2013年1月黄山（金皖烟）销量的真实值为13979万根。给出采用不同数据变换方法的2013年1月黄山（金皖烟）的销量预测值及误差值（如表2）。

表2 预测值对比表

根据表2我们发现，基于指数函数-对数函数变换法的大大提高了预测结果的精准性，在一定程度上验证了该改进灰色模型所具有的优越性。

4 结束语

烟草企业能否充分利用资源实现其利益最大化，预测客户的未来需求，判断各种烟草产品的未来销量走势尤为关键。预测的方法必须根据实际情况，着重从销量走势及预测精确度等方面进行合理的货源订制。本文通过采用改进后的灰色预测模型，对烟草产品的销量做出预测并给出以下结论：

（1）灰色预测模型适用于数量少的数据的短期预测，但对于非光滑数据列，传统的灰色模型预测精准度并不高，通过采用基于指数函数-对数函数变换法的模型对企业某商品2013年1月月销量进行预测。其相对误差率在1%左右，与传统方法相比，能够较为准确地预测烟草产品的销量及未来趋势。

（2）由于烟草行业仍实行着较为严格的计划经济管理方式——以卷烟生产计划指标严格控制着各地各企业的卷烟分配及 “区域喜好”不同等客观原因，可能会造成部分烟草产品的预测销量与真实销量有所出入，但总的销量走势不会有太大的变化。

[1]邓聚龙.灰色控制系统[J].华中科技大学学报：自然科学版,1982(3):9-18.

[2]邓聚龙.灰色系统的模型[J].模糊数学,1985,4(2):5-8.

[3]陈捷涛.灰色预测模型的一种拓广[J].系统工程，1990,8(4):50-52.

[4]李群.灰色预测模型的进一步拓广[J].系统工程理论与实践，1993,13(1):64-66.

[5]王建根，李春生.灰色预测模型的一个注记[J].系统工程，1996,14(4):14-16.

[6]吕林正，吴文江.灰色模型优化探讨[J].系统工程理论与实践，2001,21(8):92-96.

[7]何斌，蒙清.灰色预测模型拓广方法研究[J].系统工程理论与实践，2002,22(9):137-140.

[8]张军.灰色预测模型的改进及其应用[D].西安:西安理工大学，2008.

[责任编辑：桂传友]

O21

A

1674-1104(2014)03-0018-04

10.13420/j.cnki.jczu.2014.03.005

2013-10-17

池州市烟草公司科技项目应用研究；安徽省池州学院院级科研项目（2013ZR019）。

张敏珏（1984-），女，安徽池州人，池州学院数学与计算机科学系教师，硕士研究生，研究方向为数理统计;帅小应（1973-），男，安徽池州人，池州学院数学与计算机科学系教授，博士，研究方向为无线网络技术。