基于OpenGL乒乓球机器人手臂分解加速度仿真

汤志贵，冉庆泽，张学锋，陈业斌，赵帼英

（安徽工业大学a.计算机科学与技术学院；b.机械工程学院，安徽马鞍山243032）

基于OpenGL乒乓球机器人手臂分解加速度仿真

汤志贵a，冉庆泽b，张学锋a，陈业斌a，赵帼英a

（安徽工业大学a.计算机科学与技术学院；b.机械工程学院，安徽马鞍山243032）

为提高6自由度乒乓球机器人手臂的击球命中率，在Windows框架下，利用OpenGL和C++的混合编程建立了机器人手臂模型，并运用分解加速度控制算法和函数插值算法对机械手臂末端进行轨迹规划控制，实现了手臂末端沿直线和抛物线2种轨迹运动。仿真结果表明，分解加速度控制算法能够提高手臂击球的命中率。

乒乓球机器人手臂；分解加速度控制；OpenGL；抛物线；仿真

随着科学技术的不断发展，机器人其应用领域不断的拓宽[1-2]。乒乓球机器人手臂集机械、控制、图像处理等为一身的手眼协调系统近几年来引起研究者的广泛兴趣，其中机械手臂的设计和控制在研究中处于重要的地位。以乒乓球拍作为末端执行器的仿人机器人手臂需要在特定时刻，以特定的速度、特定的末端姿态到达特定的击球位置，动作完成的精度对回球效果有着指数级的影响[3]。然而这些性能指标的实现不仅需要快速的图像处理，高性能的轨迹规划算法也是必不可少的。在笛卡尔坐标空间中，需要规划出机器人末端执行器的位置函数，在关节空间中，需要规划关节变量的时间函数[4]。为实现执行器的末端能够沿着乒乓球的二次抛物线轨迹做反向运动，进而在很大程度上提高击球命中率，文中采用函数插值算法在笛卡尔坐标空间中对运动轨迹进行规划。在已经规划出机器人手臂末端笛卡尔加速度的前提下，能否通过逆运算得到关节加速度，以及用何种算法进行求取成为问题的关键点。分解加速度控制是直接求解方法之一，该方法控制精度较高，而且抗干扰能力强。

本文以OpenGL[5]为工具，对乒乓球机器人手臂进行仿真，验证分解加速度控制的有效性和可行性。

1 分解加速度控制

分解运动加速度控制通过执行器末端的笛卡尔坐标加速度来获取相应的关节加速度，再按照动力学方程计算控制力矩，对于一般的空间6自由度机器人手臂而言，其末端执行器的速度可描述为

为表示笛卡尔坐标加速度和关节加速度的关系，对式(1)两边关于时间求导，则

其中：kv代表速度增益；kp代表位置增益；e(t)代表末端执行器的位置和姿态偏差。经参数整定，即可获取合适的增益值，使系统保持稳定。

然而对一般机器人手臂而言，无法直接给出当前的关节加速度θ̈n(t)，所以必须利用上一采样时刻的笛卡尔加速度来求取上一时刻的关节加速度θ̈o(t)。对式(2)移项并求解雅克比矩阵的逆矩阵即可得：

其中：θo(t)为上一时刻的关节角度值，θ̇o(t)为上一时刻的关节角速度值。通过积分即可得到当前的关节角速度和关节角度值。假定采样时间为tp，积分公式可表述为

根据所得到的角度值θn(t)可在每一个仿真周期内对机器人发送命令，更新相应的参数值，其中关节参数值的更新可表述为

更新的参数值可作为实际值，参与到下一次的循环中，直到仿真结束，这一过程即分解加速度控制。

2 模型建立与运动学分析

2.1 手臂模型的建立

以空间六自由度乒乓球机器人手臂为例建模。模型简化如图1所示，在该模型中手臂肩部包含俯仰、滚动和偏摆3个自由度，肘部包含1个滚动自由度，腕部包含滚动和偏摆2个自由度。各自由度所对应的关节轴矢量分别用ai(i=1～6)来表示。其中D，L1，L2分别代表机械臂的肩宽、上臂(肩肘距)、下臂(肘腕距)，L3代表腕部伸出长度(含球拍的长度)，B代表球拍的厚度。∑w代表全局坐标系，Η代表机械手臂相对于基座的高度值。

为进行分析实验，针对该种模型的机械手臂，在结构设计中采用了日本Harmonic公司的谐波减速器和瑞士Maxson公司的直流电动机[6]，并利用专业的CAD软件UG设计出兵乓球机器人手臂的三维实体模型（图2），该实体模型中手臂肩部包含了俯仰、滚动和偏摆3个自由度，肘部包含1个滚动自由度，腕部包含1个滚动和一个偏摆自由度。

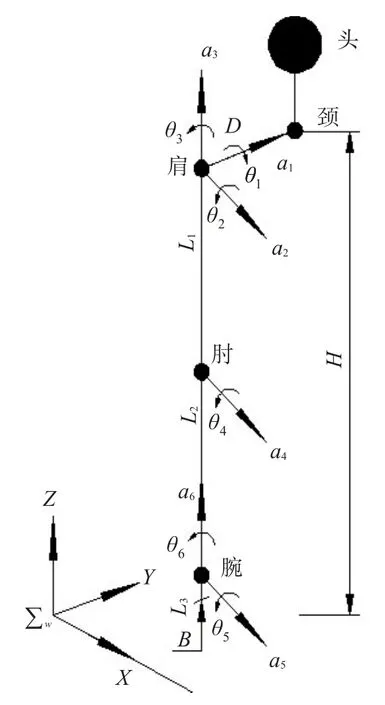
图1 乒乓球机械手臂模型简化图Fig.1 Sim p lified diagram of ping-pangmechanicalarm m odel

图2 乒乓球机器人手臂三维模型Fig.2 3Dmodelof ping-pang robotarm

2.2 正运动学分析

机器人运动学描述机器人关节与组成机器人的各个刚体之间相对运动关系，是机器人末端工具的直角坐标空间与机器人关节空间之间进行转换的桥梁[7-8]。根据图1中的简化模型，通过各仿真时刻所更新的关节角度值列写两相邻连杆的齐次变换矩阵，便可获取其运动学方程，进而得到球拍末端的位姿。

2.3 逆运动学分析

在实际的模型建立过程中为了对机器人手臂进行轨迹规划和实时控制，必须进行逆运动学求解。若已知机器人手臂末端执行器的坐标位置，则可以通过该位置坐标计算出其手臂各个关节角度值。将以上求解关节角度值的过程称为求解逆运动学问题[9]。逆运动学求解一般有解析法和数值法2种，为提高求解速度采用解析法。并且考虑篇幅的因素，这里只讨论用矩阵变换法对腕关节的滚动和偏摆2个自由度进行求解。

图3为腕关节角求解图，其中(P1,R1),(P2,R2),(P6,R6)分别代表在世界坐标系中机器人手臂的颈部、肩部、腕部的位姿。则肩关节坐标系原点在腕关节坐标系中的位置矢量可描述为

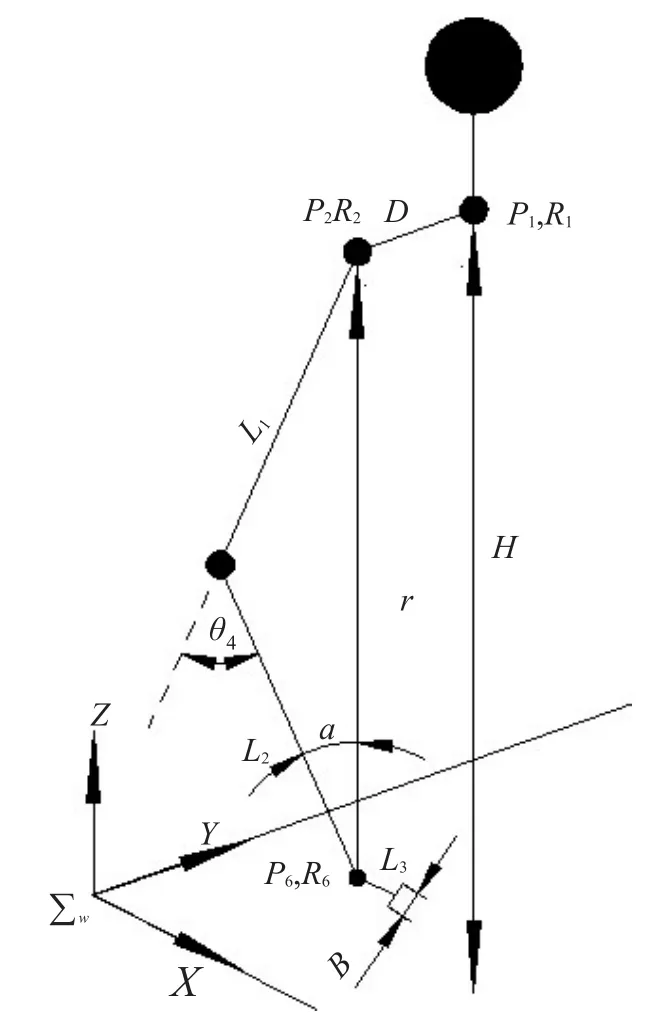
图3 腕关节角的求解Fig.3 Solution on w rist jointangle

现假定腕部两个关节不转动，则腕部的姿态即为肘关节的姿态。此时令肩关节坐标原点在腕关节坐标系中的位置矢量为

则根据旋转变换理论有

其中R表示绕某个坐标轴的旋转变换。

化简可得cosθ6rx-sinθ6ry=0 于是可解出θ6：

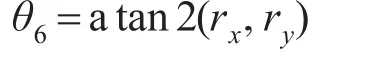
现在来求θ5

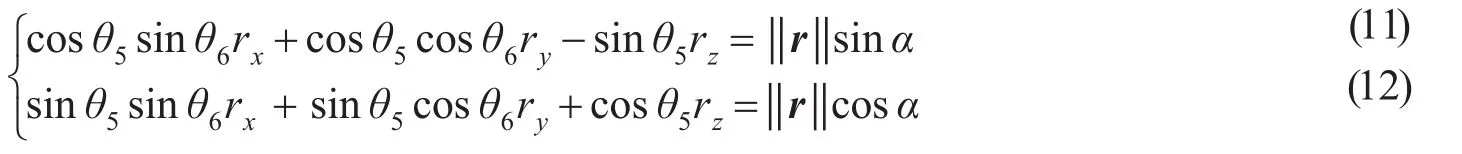
由式(11)×cosθ5-式(12)×sinθ5

考虑到机械手臂的关节受活动空间的限制，这里取

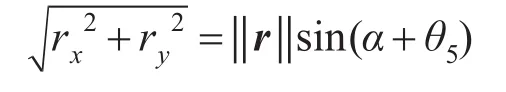
析出θ5为

2.4 运动轨迹规划算法

直线路径轨迹规划算法是机械手臂末端沿直线运动到预定位置的一种算法。在实际路径规划中需给出起始点和目标点的位姿、速度和加速度，以及运动时间等参数。考虑到轨迹的平顺性，以及过渡的平稳性，这里将起始点和目标点的速度与加速度都设置为0，为实现对机械手臂末端位置进行轨迹控制，采用的正弦函数插值公式可表示为

Am=2.0π Di/(ts×ts)。式中Di表示起始点和目标点的距离，Ds表示各采样时刻手臂末端与起点间的距离，ts表示手臂末端从起点运动到目标点所需时间，tp表示采样时间。

对式(13)关于采样时间求导，即可得机械手臂的末端速度值ve

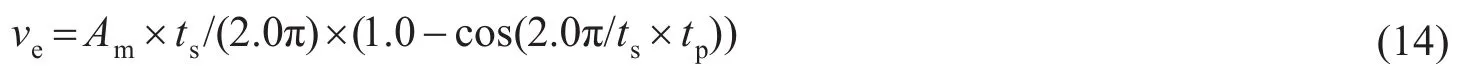
对式(14)关于采样时间求导，即可得机械手臂的末端加速度值ac

为实现对机械手臂末端姿态进行控制，这里同样采用了正弦函数插值算法，表达式和式(13)、(14)、(15)相同，只是这里的Am=2.0πAg/(ts×ts)，其中Ag是根据起点姿态和目标点姿态所求得的等效转角。将所得结果在笛卡尔坐标系下进行分解，并进行逆运动学求解，便可得到各采样时刻期望的手臂末端关节运动参数。进而根据分解加速度控制算法获得实际的关节运动参数，来控制机械手臂的运动。

抛物线路径轨迹规划算法采用的是五次多项式插值，其思想和正弦函数插值相似，故不再详述。

3 仿真与结果分析

3.1 仿真参数设定

乒乓球机器人手臂的运动复杂多样，这里仅以(5.0，-1.0，2.9)作为击球点目标位置，(1.0，1.0,1.0)作为击球点速度的手臂运动学仿真。为了满足机器人手臂响应的及时性，整个仿真规划时间为ts=2 000ms，采样时间tp=2ms。规划运动分为2个阶段：1）0～1 200ms之间，手臂末端沿直线运动到准备击球的位置；2）1 200～2 000ms之间，手臂末端沿抛物线轨迹运动到目标位置，击打乒乓球。

3.2 OpenGL仿真结果

仿真结果如下：

1）球拍末端沿直线轨迹运动的仿真结果(仿真时间T=0～1.2 s)如图4所示。

2）球拍末端沿抛物线轨迹运动的仿真结果(仿真时间T=1.2～2.0 s)如图5所示。

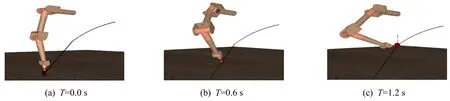
图4 直线轨迹不同时刻球拍的运动位姿Fig.4 Racketmotion posture in different time on the straight line trajectory

图5 抛物线轨迹不同时刻球拍的运动位姿Fig.5 Racketmotion posture in different timeon the parabolic trajectory

3.3 仿真结果与分析

图6为在Matlab环境下通过编写M文件得到的各关节角度随时间变化关系。

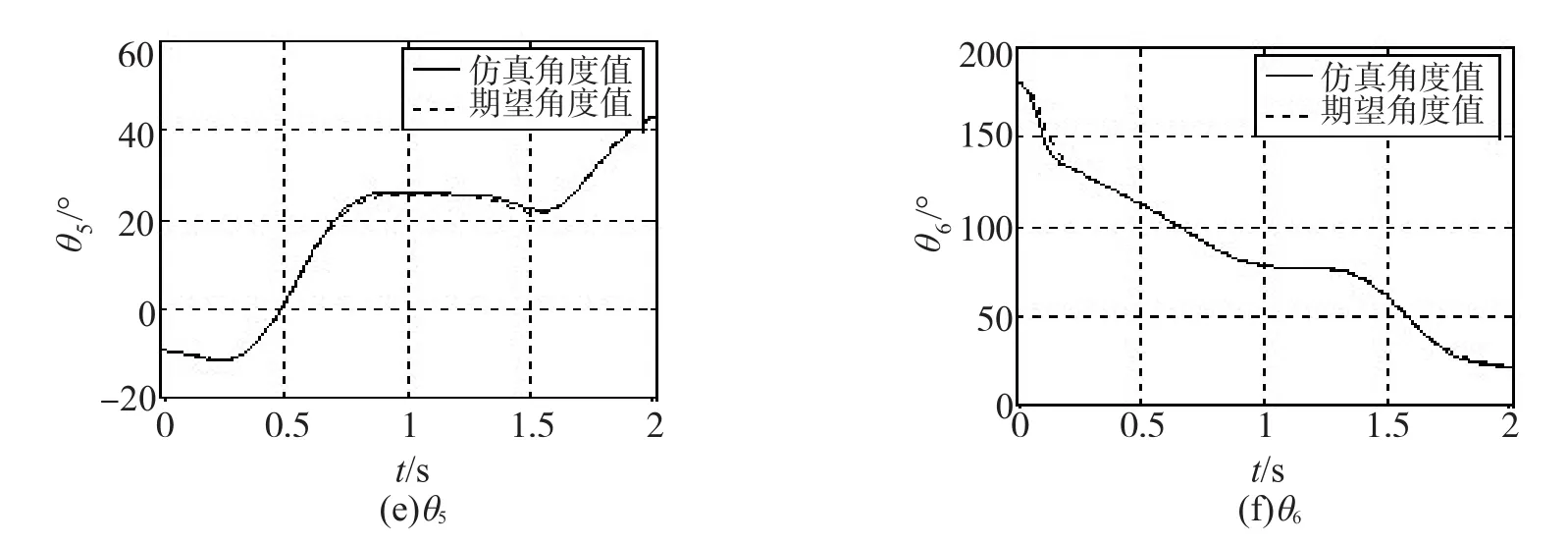
图6 不同关节角度随时间变化关系Fig.6 Changes in relationshipsof different jointangleover time

由图4到图5可以看出：乒乓球机器人手臂末端能够分别沿着直线轨迹和抛物线轨迹运动，最终到达所期望的位置。由图6可以看出：机器人手臂各关节运动平稳，且在时间T=1.2 s时曲线平滑过渡，因此不会对机械手臂产生柔性和刚性冲击。从图中还可看出：实际的关节角度值能够很好的跟踪期望的关节角度值；且在仿真结束时(T=2.0 s)，曲线斜率不为零，表明机器人手臂能够以一定的速度击打乒乓球；仿真和期望的角度值之差很小，表明能够到达所期望的位姿。以上结果均表明了分解加速度控制的有效性和可行性。

4 结语

通过对六自由度乒乓球机器人手臂的运动学建模，并在Windows环境下用基于OpenGL的C++混合编程进行了乒乓球机器人手臂的运动仿真，验证了分解加速度控制的正确性和可行性。一方面，可以看出OpenGL和C++混合编程为仿真分析提供了很好的可视化效果，使仿真从单纯的数字化中走出来。另一方面，分解加速度控制能够很好的实现乒乓球机器人的手臂完成击球动作，在乒乓球机器人手臂的控制仿真中具有一定的理论指导意义。

[1]朱旭义.工业机器人的发展与应用新趋势研究[J].数字化用户,2013(17):17-19.

[2]王孝义,周军,邱晗,等.类两足步行机构行走性能实验研究[J].安徽工业大学学报：自然科学版,2013,30(4):414-418.

[3]熊国辉.基于OPENGL技术6R机器人的仿真[D].北京：北京邮电大学,2006.

[4]勾治践,解艳超,牛永康,王成.六自由度电焊机器人平顺轨迹仿真研究[J].计算机仿真，2013,30(4):296-297.

[5]郝矿荣,孟飞,朱玉蓉.基于OpenGL的6R工业机器人动态仿真[J].工业控制计算机,2003,16(6):25-27.

[6]余金桂.减速器选型专家系统研究与实现[D].武汉：武汉科技大学,2012.

[7]陈素丽,任福深.基于OPENGL的弧焊机器人仿真设计[J].计算机技术,2012,12(3):548-550.

[8]陈富强,邱晗,刘京亮,等.基于半转机构的类两足步行机构相对运动空间分析[J].安徽工业大学学报：自然科学版,2013, 30(2):154-158.

[9]董天平,马燕,刘伦鹏.基于OPENGL的工业化机器人仿真研究[J].重庆师范大学学报,2013,30(2):60-64.

责任编辑：丁吉海

Simulation of theAcceleration Decomposition Controlof Table Tennis RobotArm Based on OpenGL

TANG Zhiguia,RAN Qingzeb,ZHANG Xuefenga,CHEN Yebina,ZHAO Guoyinga
(a.Schoolof Computer Science and Technology；b.SchoolofMechanical Engineering,AnhuiUniversity of Technology,Ma'anshan 243032,China)

To improve the batting hit rate of six-degree-of-freedom ping-pang robotarm,amodel of robotarm is constructed withm ixed programm ing of OpenGL and C++in the frame ofWindows.Decomposing acceleration control algorithm and function interpolation algorithm are used for trajectory planning and controlling the end of the mechanical arm.The end of the arm moving along a straight line trajectory and a parabolic trajectory is implemented in themodel.Simulation results show thatdecomposing acceleration controlalgorithm can improve the hit rate of robotarm batting.

table tennis robotarm;acceleration decomposition control;OpenGL;parabola;simulation

TP241

A

10.3969/j.issn.1671-7872.2014.02.014

1671-7872(2014)02-0167-06

2013-06-04

安徽省自然科学基金（1308085QF113）

汤志贵(1963-)，男，安徽当涂人，高级实验师，研究方向为网络安全和机器人设计。