基于最小能量原理计算高速切削过程中的剪切角

倪宏超，朱国辉

(安徽工业大学材料科学与工程学院，安徽马鞍山243002)

基于最小能量原理计算高速切削过程中的剪切角

倪宏超，朱国辉

(安徽工业大学材料科学与工程学院，安徽马鞍山243002)

以Oxley模型的切削力和切削几何关系为基础，提出通过计算切削过程中第一形变区、第二形变区的应力和应变来计算塑性变形功，从而构建随着切削过程中剪切角的变化，系统总能量变化规律的计算模型。基于最小能量原理，确定对应切削过程中塑性变形功最低时的剪切角为平衡剪切角。在模型中引入Johnson-Cook本构方程与动态流变应力本构方程，以文献中45钢的切削实验数据为依据，分别计算引入2种本构方程的基于最小能量原理模型的剪切角，并将计算结果与Oxley模型的计算结果进行对比分析，结果表明文中构建模型的计算结果与实验结果吻合较好。

Oxley模型；剪切角；塑性变形功；最小能量

金属切削过程中，刀具通过切削刃和前刀面挤压工件使被切削的金属发生剪切滑移。剪切角被定义为剪切面与切削速度之前的夹角[1]，剪切角的大小不仅影响切削力的大小、刀具和切屑根部的接触长度，还会影响前刀面上的应力分布，此外，剪切角还能用于反映切削变形程度。因此计算和预测剪切角的大小，对于制定合理的切削工艺，优化切削过程中的几何参数，定量分析切削过程等具有重要意义。

众多学者针对剪切角进行了研究，典型的切削模型有Merchant力平衡模型[2]、Lee-Shaffer滑移线场模型[3]、Shaw周期断裂模型[4]、Rowe和Spick修正型Mechant模型[5]、Oxley切削分析模型[6]等。这些模型中，Oxley等构建了反映切削过程中应变速率、应变及温度的金属材料流变应力本构方程，这些方程更贴近实际情况地反映了材料在切削中的力学行为，使剪切角计算精度和可靠度得到提高。然而在Oxley模型中仍存在一些不足，且部分研究者为此进行了完善，如：Huang等[7]通过引入移动热源，改进了Oxley切削模型中2个形变区域温度的计算方法；Adibi等[8]对比了不同类型本构模型对Oxley切削模型计算结果的影响；Karpat等[9]细化构建了刀屑界面粘结摩擦区。文中根据Oxley切削模型中平衡剪切角的力平衡判据，从材料切削形变塑性功能量最小的角度对该判据进行修正，以进一步完善Oxley切削模型，此外还对比研究不同本构方程对计算结果的影响。

1 Oxlye切削模型修正

Oxley切削模型是基于切削稳态时力平衡、卡片切削模型以及部分滑移线场理论，引入切削速度、温度修正应力以反映材料切削中力学行为的本构方程，提出的平行侧面剪切区切削分析模型如图1。由图1可知：被加工材料在流经第一形变区域时，在刀尖刃口的作用下实现被切削层与工件的分离；随后在刀具挤压作用下，在剪切平面AB上发生塑性形变，变成切屑；然后切屑沿刀具前刀面切向方向继续运动。Oxley切削模型中用于计算剪切角的判据是力平衡，即宏观切削力在刀屑界面上分力所导致的切应力值与使得刀屑界面上以一定应变及应变速率发生塑性形变时的剪切应力相等。然而系统的运行总是自发地朝能量最小状态进行，刀具对材料切削的实现是通过使被切削层在第一形变区和第二形变区塑性形变而完成的。故在生成切屑过程中，2个形变区域的塑性功总和构成了切削所用的能量，从切削能量最小观点出发，平衡剪切角就是塑性变形功最小时对应的剪切角。据此文中从该观点出发修正Oxley切削模型中的力平衡判据。

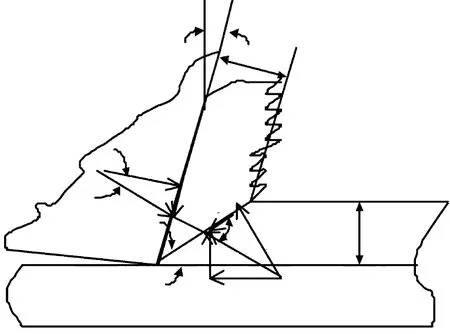
图1 Oxley模型中的力学关系Fig.1 Force diagram in Oxley cuttingmodel

1.1 第一形变区能量计算

金属材料受外力作用发生塑性形变时，外力做功的能量一部分用于改变金属材料内部微观组织结构，另一部分则使形变基体产生温升，外力做功值与塑性形变功相等。令kAB为AB面上的剪切流变应力，εAB为AB面上的平均应变，第一形变区的塑性变形功WP表达为

据M ises屈服准则可得，剪切流变应力kAB与AB面上的流变应力σAB，剪切应变εAB与AB面上的真应变γAB间的关系式为：

由图1所示Oxley切削分析模型图中的几何关系，可以得到γAB的计算式为

其中：γ0为刀具的前角；φ为切削过程中的剪切角。Oxley构建的切削模型中，σ为材料的流变应力，被加工材料力学行为的本构方程满足指数关系形式，如

其中参数σ1和n为式(6)所示切削速度修正温度Tmod的函数，

其中：参数ε̇e为与材料相关的常数；v为切削速度，对于碳钢其值介于0.09～1之间。为得到σ1和n与Tmod间的表达式，Oxley等采用高阶多项式拟合二者关系，这一方面弱化了本构方程的物理意义，另一方面计算精度依赖多项式拟合结果。在众多的本构方程中，Johnson-Cook是基于材料强度应变项、应变速度项和形变温度项三者的乘积作用而提出的本构方程，因该本构方程形式简单，参数较易求解，使用方便而被广泛使用。

当使用Johnson-Cook方程表述材料本构关系时，其表达式为

式中：A，B，C，m，n为材料参数；Tw为工件的初始温度；TM为材料熔点；ε̇0为相对应变速度。用式(2)计算材料在第一形变区的应力，需得到切削过程中第一形变区的应变速度和形变温度。Oxley模型指出，第一形变区的平均应变速度ε̇AB可以表达为

式中：γ̇int为第一形变区的应变速度；C0为剪切区长度与第一形变区厚度的比值；vs为剪切速度；l为剪切平面AB的长度。在塑性变形过程中，形变功的一部分用来赋予材料的切削变形，另一部分则转变成热量。总热量的一部分通过热传导进入被加工工件，余下部分致使第一形变区的温度升高。因此使用式(7)计算第一形变区流变应力时，形变温度并不是工件温度。设ΔTSZ为剪切区域的温升，第一形变区中转化为ΔTSZ热量的塑性功占总量的比值为η，通过热传导进入工件的热量占总热量的比值为β，利用基础比热公式对每单位切屑的温升进行积分，可以求解出第一形变区的温升ΔTSZ为

式中：mchip为单位时间内的切屑质量；CP为工件材料的比热。β的计算式如下式中ρ，RT，K分别为工件材料密度、热量系数和导热系数。根据上述的讨论，假设温度主要在剪切面上，则第一形变区中的温度可以计算为

联立式(1)～(12)，可以计算出切削过程中随着剪切角转动，第一形变区中的应力、应变、应变速度和温度，进而得到其塑性变形功随剪切角转动的规律。

1.2 第二形变区能量计算

根据Oxley模型[10]，假设刀具与切屑接触面上的剪切流变应力为kchip，接触面上的平均剪切应变为εint，则第二形变区的塑性功WS可表示为

采用M ises屈服准则，可得剪切应力kchip和剪切应变εint与流变应力σint和应变γint间转换关系：

γint为刀具和切屑接触面上的剪切应变，计算式为[10]

其中γM为接触面上的最大剪切应变，可表示为

式中：t2为切屑厚度；h为刀具和切削的接触长度，其计算公式为neq是应变硬化指数，可以表示为

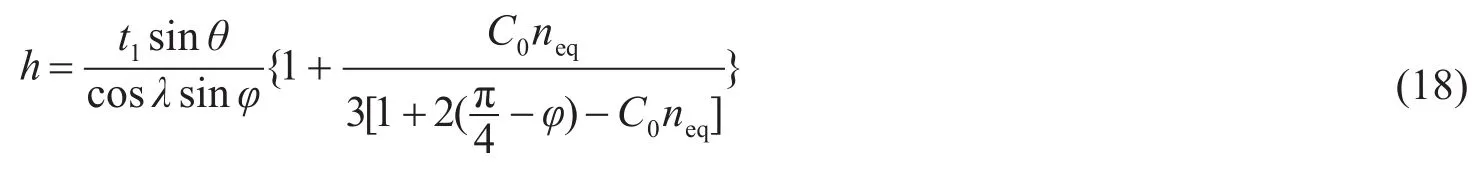
沿用计算第一形变区塑性功的思路，为了修正Oxley的模型，文中同样引入Johnson-Cook模型表述材料的本构关系，则第二形变区的应变速度可表示为

其中：ε̇int为接触面上的平均剪切应变速度；γ̇int为接触面上的剪切应变速度；vc为切屑的速度；δ为接触面塑性区厚度和切屑厚度的比值。同样在第二形变区的形变功也有一部分会导致刀具和材料界面的温度升高。第二形变区域的温升是在第一形变区域温升之后，进一步因刀屑界面上的摩擦作用而升高，因此刀具和工件材料界面的平均温度计算式为

其中：ΔTM为刀具和切屑接触面上最大的温升；ψ为保证Tint为平均值的温度因素，一般为0.9。Boothroyd[11]假设接触面上为矩形热源，推导出接触面上最大温升ΔTM，表示为

其中ΔTC为切屑上的平均温升，经过对接触面上单位切屑温升的积分可以推导得出

根据上述的讨论，可以分析计算随着切削过程的进行，剪切角转动与第二形变区能量变化之间的关系。

1.3 切削过程中剪切角的转动与切削总能量的计算

刀具切削金属材料过程中的能量耗散由两部分构成，分别为第一形变区与第二形变区的塑性功。故第一形变区与第二形变区的能量总和WT可以表示为

由上述2节可计算出给定切削条件下第一形变区塑性功WP，第二形变区塑性功WS以及总的切削消耗能WT。根据构建的计算模型，对切削过程中的剪切角进行计算。

2 模型验证与讨论

Ivester等[12]使用OKUMACadet-L1420X650CNC，Lelond Makino Baron 60 Lathe和Okuma LC-20 Lathe 3种切削机床分别对45钢进行正交切削实验，其实验条件及结果如表1。文中以其实验参数为依据输入新构建的基于最小能量原理的模型，输出模型计算的剪切角，对比实验结果，以验证模型的正确性。

表1 45钢正交切削的实验条件及实验结果Tab.1 Conditionsand resultsof 45 steelorthogonal cutting of experimental

为了说明引入的本构方程对新建模型计算结果的影响，分别在模型中引入Johnson-Cook本构方程以及流变应力本构方程进行计算，对比计算结果。式(7)中Johnson-Cook本构方程参数源于Jaspers等[13]的研究结果，其方程参数A，B，C，m，n分别为553.1MPa，600.8MPa，0.013 4，1，0.234。45钢动态流变应力模型方程为

其中σ0，n，A，B，ε̇0及T0为动态流变应力本构方程参数，分别为278.3MPa，0.101，0.176，0.000 032，1和274 K。45钢的比热CP、热导率K分别按下式计算

用Matlab编程软件，结合表1中正交切削实验工艺参数、45钢Johnson-Cook本构方程和动态流变应力本构方程以及45钢热物性参数，编写程序运算，得到Ⅰ,Ⅱ组2种切削条件下的切削过程中，2个形变区的能量及总能量随剪切角的变化规律，结果如图2，3。

图2 采用Johnson-Cook本构方程计算出的WP，WS和WT随剪切角的变化曲线Fig.2 Changsof WP，WSand WTcalculated by Johnson-Cook constitutivemodelwith shear angle

图3 采用动态流变应力本构方程计算出的WP，WS和WT随剪切角的变化曲线Fig.3 Changsof WP，WSand WTcalculated by 45 steel flow stressmodelwith shear angle

从图2，3可以看出，虽然本构模型形式不同，但所得规律较为相似。切削过程中，第一形变区能量WP随着剪切角减小逐渐增大，第二形变区能量WS随着剪切角减小先减后增，2个形变区的能量总和WT在5°～40°的剪切角范围内呈现抛物线状，根据切削能量最小原理，能量总和WT的最低点对应的剪切角即为切削达到稳态时的平衡剪切角。表2给出了实验结果，Oxley模型[14]计算结果及分别引入2种本构方程所构建的基于最小能量原理模型计算出的平衡剪切角。

表2 采用不同模型计算的45钢平衡剪切角及实验结果Tab.2 Equilibrium shear angleof45 steelondifferent calculationsand experiments

从表2可以看出：与实验结果相比，应用Oxely模型计算出的平衡剪切角偏大，平均相对误差达到了42.8%；引入2种本构方程的模型计算结果略有差异，但计算结果更接近实际测量值，用动态流变应力本构方程所得计算结果的平均相对误差为21.6%，而Johnson-Cook本构方程的相对误差仅6.0%。主要原因是Johnson-Cook本构方程中温度对流变应力的影响处理方法，较动态流变应力本构方程的要好，使得采用Johnson-Cook本构方程描述45钢极高应变速率下形变力学行为更为准确。因此，采用引入Johnson-Cook本构方程构建的基于最小能量原理模型计算切削过程中平衡剪切角值较为恰当。

3 结论

以Oxley的切削力和切削几何为基础，基于切削形变功的能量最低法则，提出以第一形变区和第二形变区的形变功总和最低确定平衡剪切角的计算模型。在本文的模型中，对于材料的应力应变方程，利用Johnson-Cook本构方程和动态流变应力本构方程来表述材料的本构关系，更接近实际地描述形变温度和应变速度对材料强度的影响。通过Ivster对45钢的正交切削实验结果，对本文提出的模型进行了验证，结果表明基于最小能量原理，并引入Johnson-Cook本构方程计算平衡剪切角，其平均相对误差最小。

[1]付秀丽，艾兴，刘占强，等.高速切削加工铝航空合金7050-T7451剪切角模型的研究[J].中国机械工程，2007(2):220-225.

[2]MerchantM E.Mechanicsof themetalcutting process[J].Appl Phys,1945,16(5):267-275.

[3]Lee EH,Shaffer BW.The theory of plasticity applied to a problem ofmachining[J].ApplMech,1951,73:405-413.

[4]Shaw M C.MetalCutting Principles[M].Oxford:Oxford University Press,2005:237-246.

[5]Rowe GW,Spick P T.A new approach to determ ination of the shear-plane angle in machining[J].Journal of Engineering for Industry,1967(89):530-538.

[6]Oxley PLB,Welsh M JM.An explanation of apparentbridgman effect inmerchant’s orthogonal cutting results[J].TransASME, 1987,89(2):103-111.

[7]Huang Y,Liang SY.Cutting forcesmodeling considering the effectof tool thermal property application to CBN hard turning[J]. International JournalofMachine Toolsand Manufacture,2003,43:307-315.

[8]Adibi-Sedeh A H,Madhavan V,Bahr B.Extension of Oxley’s analysis ofmachining to use differentmaterialmodels[J].Journal ofManufacturing Science and Engineering,2003,125:656-666.

[9]KarpatY,Ozel T.Predictive analyticaland thermalmodeling oforthogonal cutting processpart Ipredictionsof tool forces,stresses and temperature distributions[J].JournalofManufacturing Scienceand Engineering,2006,128:435-444.

[10]Oxley PLB.TheMechanicsofMachining:An AnalyticalApproach to Assessing Machinability[M].England:Ellis Horwood Ltd, 1989:213-215.

[11]Boothroyd G.Temperatures in orthogonalmetal cutting[J].Proceedings of the Institution of Mechanical Engineers,1963,177: 789-810.

[12]Ivester RW,Kennedy M,DaviesM,etal.Assessmentofmachiningmodels:Progressreport[J].Machining Scienceand Technology, 2000,4:511-538.

[13]Jaspers SPFC,Dautzenberg JH.Materialbehaviour in conditions sim ilar tometalcutting:Flow stress in the primary shear zone [J].JournalofMaterials Processing Technology,2002,122:322-330.

[14]LalwaniD I,Mehta N K.Extension of Oxley’s predictivemachining theory for johnson and cook flow stressmodel[J].Journal of Materials Processing Technology,2009,5:305-312.

责任编辑：何莉

Modeling of ShearAngle Calculation Based on Minimum of Plastic Deformation Energy

NIHongchao，ZHU Guohui
(SchoolofMaterialsScienceand Engineering,AnhuiUniversity of Technology,Ma'anshan 243002,China)

Based on the relationship of cutting force and cutting geometry developed by Oxley,effect of plastic deformation energy on the primary shear zone and secondary shear zone on the shear anglewas analyzed through calculation of stressand strain on the primary and secondary shear zone during high speedmachining.Equilibrium shearanglewasdefined ascorresponding tominimum of totalplastic deformation energy.Introducing Johnson-Cook constitutive equations and dynam ic flow stress constitutive equation in themodel to calculate the shear angle of m inimum energy based on the experimental resultsof 45 steeland compare the calculationwith the resultof Oxley model.Itcould be seen that the calculation from the presentmodel is in good agreementwith the experimental results.

Oxley cuttingmodel;shearangle;plasticwork;m inimum energy

TG115

A

10.3969/j.issn.1671-7872.2014.02.004

1671-7872(2014)02-0120-06

2013-11-06

国家自然科学基金项目(51175003)

倪宏超(1987-)，男，河北保定人，硕士生，主要从事切削过程中剪切角模型的研究。

朱国辉(1959-)，男，上海人，教授，主要从事先进材料及工艺开发的研究。