船舶静水航行水动力模型的简化及其应用

许玲，邱晗

(安徽工业大学机械工程学院，安徽马鞍山243032)

船舶静水航行水动力模型的简化及其应用

许玲，邱晗

(安徽工业大学机械工程学院，安徽马鞍山243032)

针对现有船舶水动力模型考虑因素多、通用性差的缺点，通过简化船体线形、忽略波浪和风向等复杂因素的影响，对船舶水动力模型进行研究。推导静水面船体的迎流区域范围，计算水流作用在船体微小面元上的动压力，得出整船水流总阻力计算模型。在此基础上，给出船体航行动力学模型，分析船舶在静水面航行中动力、水阻力和运动状态之间的关系。将该水动力模型应用于船舶稳定航行控制，结果表明模型具有较好的实用性。

静水面；船舶航行；水动力模型；航行动力学

在船舶与船舶装置设计阶段，船舶航行性能是核心研究之一，基于水中船舶运动和载荷特性的水动力模型则是船舶航行性能分析的重要基础[1]。完善的水动力模型一般针对具体环境和应用，涉及因素多，建模过程较复杂[2-3]；另外除了相关的设计数据和建模理论外，有的还需通过大量的试验确定必要的水动力系数[4]。而大量的船舶性能仿真研究多是从建立船舶水动力模型开始[5-7]，然而，现有的水动力模型大多针对复杂水环境或具体船舶构型，建模方法通用性较差，在只对船舶的局部通用设备进行研究时，这些模型需修改后才能使用。

为在不局限于具体船型的情况下可以开展水动力分析，有必要建立通用性较强的船舶水动力模型。笔者在新型仿生船舶推进器研究[8]的基础上，为对新型推进器的推进能力与方向控制性能进行仿真研究，在无法使用现有建模方法的情况下，提出1种船舶静水面航行的简易水动力模型。该模型虽然未考虑船舶结构因素，不能精确地模拟真实船舶的运行性能，但是它有助于在推进器研究过程中及时方便地分析推进器的基本特性。通过在航行稳定控制中的应用看出，该模型具有较好的实用性。

1 面向静水面的船舶水动力模型

1.1 静水中船体简化模型及其迎流区域描述

如图1所示，船体简化为椭圆柱体，a和b分别为船体长度和宽度，β为船首与船体运动方向的偏角(以下称漂角)。当船体在静水中以速度U航行时，水流相对船体以速度-U流过(如图2所示)。水流速度分别在A,B点与船体相切，然后绕流到后侧。椭圆船体上从A逆时针到B区域为迎流区，而椭圆船体上从A顺时针到B的区域背向水流。

图1 船体椭圆模型图Fig. 1 Elliptical model of hull

图2 相对船体的水速Fig. 2 Water velocity relative to hull

船舶在水中航行时，水动力主要作用在船体入水部分的迎流区面上。由图2可见，当船首与船体运动方向的漂角β变化时，船体迎流区域将发生变化，从而导致水动力发生变化。图2中，A，B 2点是水流速度矢量与椭圆的切点，椭圆上AB之间面向水流的部分就是迎流区。

其中t0是切点(x0,y0)的参数。当切线与水流速度平行时，有kt=tanβ，即由此解得迎流区域边界点A,B对应的椭圆参数为

因此，船体迎流区域模型为

1.2 水流作用在船体微面元上的动压力

水流相对速度-U=-U cosβi-U sinβj。设椭圆船体上任一点Q(a cost，b sin t)的法线的倾斜角为θ，则该法线的斜率为保证此法线单位矢量的正方向指向椭圆外侧，取sinθ,cosθ的正负号与sin t,cos t一致。有

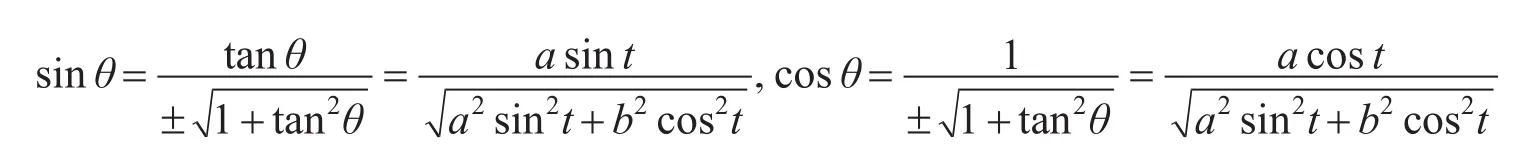
因此Q点法线方向的单位矢量为

显然，n的正方向指向椭圆外侧。水流相对速度在椭圆船体上Q点法线方向的分速度为-U·n，其方向指向椭圆内侧，大小为

由伯努利方程可进一步求得水流对船体Q点所在微面元法向上的动压力p

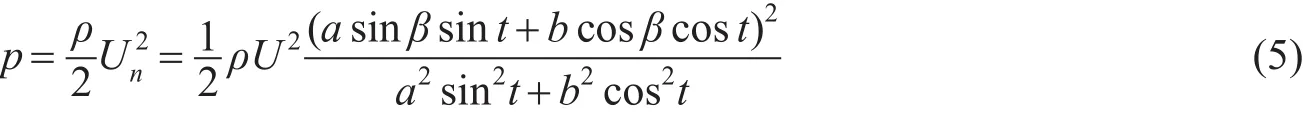
其中ρ为水密度。

1.3 整船水流总阻力计算模型

水流作用在船体面积元d A上的总阻力d F为

其中CD为实验阻力系数。令d s为船体椭圆的弧长微分，则单位高度船体的面积元d A=d s·1=d s。综合式(6)和式(3)进一步可得出

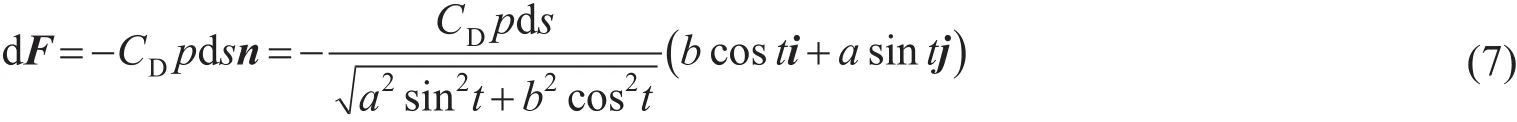
在迎流区积分可以求出单位高度船体上水的总阻力向椭圆中心C简化的主矢Rx,Ry与主矩MC为：

由式(1)，(5),(9)和(10)进一步可得整船水流总阻力的主矢与主矩计算模型分别为：

在静水面航行中，船体的运动状态在水流阻力主矢Rx,Ry,水流阻力矩MC以及主动推力与主动转向力矩综合作用下得到。如图3所示，建立固连于地面的惯性坐标系ηOξ，同时在船体上固连运动坐标系xCy。为简化模型表达，在建立船体动力学模型时仍用单位高度椭圆柱体为船体模型。

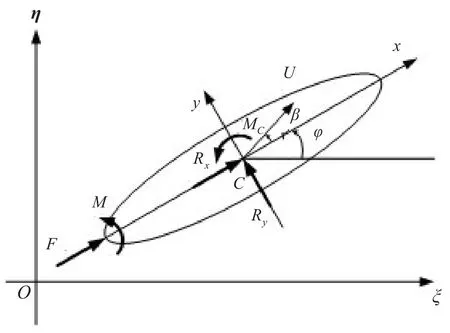
图3 船体航行动力学模型Fig.3 Dynam icmodelofhull

船体的运动是在坐标系ηOξ中的平面运动，所以其动力学方程为

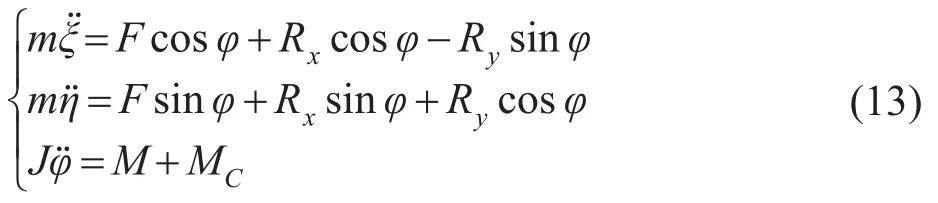
式中：m是单位高度船体的质量；J是单位高度船体对其质心C的转动惯量；F是推进器的推力与船体高度的比值；M为推进器产生的转向力矩与船体高度的比值；φ为船体的方向角。由式(11)～(13)可见，船舶在静水面航行时，船舶航行状态的主要变量是速度U、航行方向角φ与漂角β。航行驾驶系统应遵循水动力作用模型规律，通过调整推进器的推力与转向力矩来改变航行状态参数U,φ与β，从而达到稳定航行的目的。

3 船舶稳定航行的应用

船舶航行操控模式主要是直航与转向。直航的操控比较方便，保持β=0，调整推力F达到需要的速度U即可。与直航相比，转向操控要困难得多。转向时开始施加1个较小的转向力矩M，产生漂角β后，应及时根据水动力模型和船体航行动力学模型控制转向力矩M，从而控制漂角β依照合理的规律变化。若不及时适当地控制β而任其变大，由式(12)可见，水动力产生的力矩MC将越来越大，从而使转向越来越快，漂角也越来越大，船舶最终会产生自转而失去稳定。为使船舶转向的同时能够稳定航行，必须依据水动力模型制定正确的操控策略。在转向过程中随时调控F的大小以及M的大小、方向，使漂角β不要过大；同时也须使MC不能过大，以免转向过快而难以控制。

为验证上述理论，以本课题组在韦斯—福效应船舶推进器研究中的船舶样机[9]为原型(如图4)，样机船尾装有2台推进器，没有再设置舵。通过调节2台推进器的推力可以产生不同的推进力与转向力矩，从而实现直航与转向。假设在静水面航行时，向右转弯45° (即0.785 4 rad)。航行操控时设定左侧推进器转动，右侧不动。由水动力模型(式(11)，(12))和船舶动力学模型(式13)计算出漂角应控制在4°(0.07 rad)左右。图5，6分别是转向控制中的航行方向角和漂角变化情况。由图5可见，开始转舵操作后船舶即开始转向，经过5 s已转过20°(0.35 rad)，但航向尚不稳定，有较大的振荡漂角(见图6)。在操控策略的控制下，漂角振幅越来越小，航向趋于线性变化，经过20 s完成转弯动作，航行方向角达到45°(0.785 4 rad)）。由图6可见，开始转向时漂角变化较大(漂角达10°)，通过控制，5 s后漂角就小于6°，在完成转向时(第20 s)稳定在0.07 rad(4°)左右。此后沿45°方向直线航行中，漂角逐渐恢复到0，进入稳定的直线前进。以上表明，采用文中提出的水动力模型和船舶动力学模型，得出相应的漂角控制策略，可实现船舶转向稳定航行。

图4 实验船舶样机原型Fig.4 Physicalprototype of experimentalship

图5 航行方向角φ变化曲线Fig.5 Curveof navigation direction angleφ

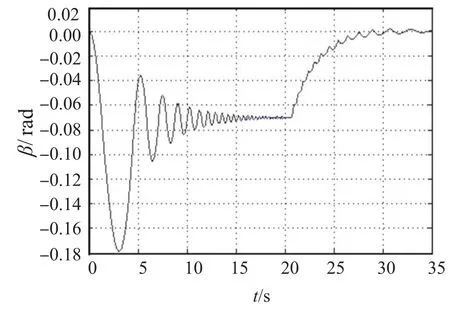
图6 漂角β变化曲线Fig.6 Curveof driftangleβ

4 结论

1)提出一个适用于静水面航行的水动力理论计算模型，由于未考虑不同的船体复杂外形结构以及复杂的水流影响，该模型是抽象和简易的，但由于将船体假设成椭圆形，在控制精度要求不高的情况下，该模型具有较好的通用性。

2)将水动力理论计算模型以及船体航行动力学模型应用于样船的稳定航行控制。应用结果表明，以上模型使用简便，具有较好的实用性，也可以在船舶航行的初步仿真计算或船舶航行效果的动画显示中使用。

[1]李殿璞.船舶运动与建模[M].北京：国防工业出版社，2008:68-108.

[2]方昭昭，朱仁传，缪国平，等.基于数值波浪水池的波浪中船舶水动力计算[J].水动力科学与进展，2012,27(5):515-524.

[3]方昭昭，赵丙乾，金武雷，等.顶浪中船舶水动力计算与运动模拟研究[J].中国舰船研究，2013,8(5):33-40.

[4]姜哲，石珣，王磊.动力定位船舶水动力参数数值试验研究[J].实验室研究与探索，2005,24(12):14-17.

[5]曾芬芳，陈晓军，林剑柠，等.基于水动力模型的船舶航态的模拟仿真[J].系统仿真学报，2001,13(3):376-380.

[6]陈宁，龚苏斌.船舶回转运动仿真[J].舰船科学技术，2013,35(3):9-14.

[7]肖凡，张涛，万峻.海洋环境中船舶运动规律的可视化仿真方法研究[J].造船技术，2010(3):43-46.

[8]张震，潘紫微，邱支振，等.基于半转机构的仿生船舶推进器的仿真研究[J].机械传动，2009,33(5):6-8.

[9]毛富志，潘紫微，邱支振.半转叶轮仿生推进船舶实验方案设计[J].机械工程师，2008(12):51-53.

责任编辑：何莉

Simplified Hydrodynam ic Modelof Ship Sailing in StillWater and itsApplication

XU Ling,QIU Han
(SchoolofMechanical Engineering,AnhuiUniversity of Technology,Ma'anshan 243032,China)

There are some shortcom ings in current hydrodynam ic models,such asmany influential factors and weak universal performance.A new and simple hydrodynam icmodelwas proposed,which ignored the shape of ship,wave ofwaterand w ind.The area of ship that faceswater flow was firstly deduced when ship sailed in static water.After calculating water flow force applied on m icro area of ship,themodel of total water resisting force applied on whole ship was further given.On the basis of the above results,dynam icmodel of ship sailing was proposed,which illustrates the relationship among drive fore,water resisting force andmotion of ship.Finally,the above models were applied to control ship steady sailing.The application of the case study shows that the hydrodynamicmodelhasbetterpracticability forsailing in staticwater.

stillwater；ship sailing；hydrodynam icmodel；sailing dynam ic

U661.1

A

10.3969/j.issn.1671-7872.2014.02.013

1671-7872(2014)02-0162-05

2013-12-27

国家高技术研究发展计划(863计划)项目(2006AA11Z226)

许玲(1962-)，女，山东泰安人，高级实验师，主要研究方向为机械设计与制造。