近似面齿轮传动的齿面拓扑修形主动设计

梁德军，彭先龙

（1.合肥江淮铸造有限责任公司 产品研发部，合肥 231137；2.西北工业大学 机电学院，西安 710072）

0 引 言

应用无进给运动的大盘形砂轮磨齿加工面齿轮具有磨齿效率高、机床传动结构简单的特点，应用国内现有的制造装备即可磨齿加工面齿轮。然而这种磨齿方法加工的面齿轮具有近似齿面，与标准的渐开线圆柱齿轮，或与有齿面修形的圆柱齿轮的啮合性能不够理想［1］。

为了确定弧齿锥齿轮，准双曲面齿轮和端面蜗杆的机床调整参数并改善这些齿轮传动的啮合性能，Litvin［2-3］提出了局部综合法，但是局部综合法只能预控参考点附近的啮合性能，因此吴训成、曹雪梅等［4-5］在局部综合法的基础上提出了主动设计法。具有近似齿面的面齿轮传动中，无论是小齿轮还是面齿轮的机床调整参数都较少，研究证明即使人为添加一些调整参数，对近似面齿轮传动的啮合性能改变也是有限的，故局部综合法或主动设计法不适宜于近似面齿轮传动的啮合性能设计。Kolivand、Yi-Pei Shih［6-7］通过预设的啮合性能来构造准双曲面、弧齿锥齿轮传动的小轮拓扑修形齿面，最后用敏感性系数矩阵确定小齿轮加工规律，达到改善啮合性能的目的。

由于齿面加工方面的差异，该方法还不能直接用于近似面齿轮传动的齿面设计中。本文主要论述如何通过构造小轮拓扑修形齿面对近似面齿轮传动进行主动设计，以控制其啮合性能。

1 面齿轮的近似齿面

采用不做齿向进给运动的盘形砂轮磨削面齿轮的原理与方法可参考文献［1］，且这里的盘形砂轮与该文献的碟形砂轮属同一概念。为节省篇幅，此处仅给出面齿轮的近似齿面Σa相对理论齿面的误差图如图1，该误差图及计算实例的参数如表1 所示。齿面误差的计算方法为：式中，n2，R2分别为面齿轮理论齿面的单位法矢、位矢。并设面齿轮近似齿面Σa的位矢和法矢分别为：Ra（us，θs）、na（us，θs）。us、θs为面齿轮近似齿面Σa的曲面参数。

图1 面齿轮近似齿面Σa 的齿面误差

2 小轮的共轭齿面与传动误差

为了使得小轮齿面Σ1与Σa共轭，将面齿轮近似齿面Σa（详见文献［1］中R2的推导）看作为展成加工小轮齿面Σ1的刀具。Σ1的展成坐标系如图2 所示。坐标系S2与Σa固联，坐标系S1与Σ1固联，Sp、Sm是与机架固联的辅助坐标系。

表1 面齿轮传动的设计参数

图2 与Σa 共轭的小轮齿面展成坐标系

γm是小轮与面齿轮的轴线夹角，L0=（L1+L2）/2，ψ1、ψ2是小轮和面齿轮各自的转角，ψ1、ψ2满足如下关系：

式中：ψ20=m21·ψ10和ψ10为选定参考点处插齿刀和面齿轮的转角，满足理论传动比m21=N1/N2，N1、N2分别为小轮和面齿轮的齿数；a1…an-1为二阶到n 阶传动误差的系数，根据传动误差设计要求确定。

传动误差是影响齿轮传动动态性能和振动的重要因素。由于二次抛物线传动误差可以吸收装配误差引起的线性误差［8］，并保持误差曲线的形状不变，因此通常将传动误差设计为抛物线，但是有些情况下，传动误差会设计为高阶函数［9］。

通过S2到S1的坐标变换和啮合方程可确定小轮齿面Σ1的位矢R1和法矢n1，分别为：

式中M12是坐标变换矩阵，Σa与Σ1间的啮合方程由下式表示：式中是表示在坐标系S2中的两轮相对速度。

由于Σa存在齿面误差，且在小轮齿面展成过程中有关系式（2），因此Σ1相对标准渐开线圆柱齿轮将存在齿面偏差（偏差的计算方法与式（1）类同），图3 所示为a1…an-1均为零时，齿面Σ1的偏差。文中将Σ1简称为小轮（与面齿轮近似齿面Σa的）共轭齿面。

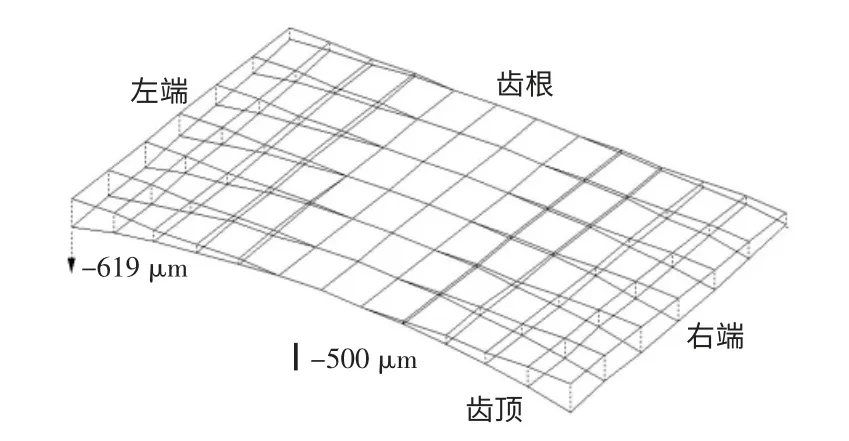
图3 Σ1 相对标准渐开线齿面的偏差（a1=…=an-1=0）

3 预设接触路径

齿面印痕的形状（包括接触路径的方向、位置和接触椭圆的长度）对齿轮的平稳运转、使用寿命和噪声有重要影响。例如接触路径的方向会影响重合度的大小［10］，影响齿轮副运转的平稳性，因此通常将接触路径设计为倾斜的，一方面可增大重合度，提高齿轮传动的平稳性，另一方面可以减小边缘接触的可能性。

图4 是Σa在其旋转投影面上的投影，预设的接触路径在旋转投影面上为直线M1M2m-1，它与水平线的夹角为θ，由θ 可确定接触路径的方向，根据啮合性能的设计要求选择。图4 中的Mi（i=m）是选定的参考点，满足方程式（6）。式中LMm、rMm为在面齿轮旋转投影面上点Mm到原点O 的距离，是参考点Mm的选定值，点Mm可以沿齿高和齿长方向移动，以获得具有对称性的传动误差。当LMm、rMm确定后，解方程（6）即可解得ψ20和ψ10。

图4 预设的接触路径

预设接触路径M1M2m-1上的其他点Mi（im，i=1…2m-1）满足式（2）和下述方程：

式中rMi是接触点Mi的齿高，按给定的等步长变化。式（7）中第一式即直线M1M2m-1的方程。解方程式（7）即可解出usi、θsi和ψ2i，可得到小齿轮上的接触路径P1P2m-1。据上可知参考点Mm在旋转投影面上的坐标、夹角θ分别确定接触路径的位置和方向。

4 小齿轮的拓扑修形齿面

接触椭圆长半轴的长度a 会对齿轮的润滑、齿面接触应力、齿根弯曲应力等产生影响，因此获得合适的接触椭圆长度是齿面设计的重要任务。接触椭圆长半轴的长度一般取0.15~0.20 倍的齿宽。

由于Σ1与Σa完全共轭，因此Σ1与Σa在每一瞬时将是线接触的，实际应用中的齿轮传动要求是点接触的，以降低对安装误差的敏感性，为此以Σ1作为基准曲面，构造小轮的拓扑修形齿面Σp。

图5 表示的是在小轮旋转投影面上拓扑修形齿面的构造过程，a 是接触椭圆长半轴的长度，根据啮合性能的设计要求选择。直线bi1、bi2（图中粗实线）与接触路径的交点为Pi1、Pi2（图中没有表示），长度为接触点Pi1、Pi2处接触椭圆长半轴的长度a，并且直线bi1、bi2与Pi1、Pi2处接触椭圆长半轴重合，直线bi1、bi2与接触点Pi所在的网格线交点 为Pi3、Pi4。接 触 路 径P1P2i-1两 侧 点Pi3、Pi4成 区 域A1A2A4A3，该区域内的齿面需要精确设计，而该区域外的齿面则可以看作为区域A1A2A4A3的延伸。接触路径P1P2m-1上的点的齿面修形量为0，即在齿面Σ1上。而bi1、bi2与网格线的交点Pi3、Pi4处的齿面修形量为δ（δ 一般取0.006 35 mm），即弹性变形量。最后用修形曲线替代直线Pi3PiPi4，构成新设计的小轮拓扑修形齿面。

图5 小轮拓扑修形齿面Σp 的构造

点Pi3、Pi4在Σ1上的齿面坐标计算步骤为：

1）计算面齿轮的主曲率与主方向、Σ1的主曲率与主方向；

2）在小轮坐标系S1中计算任意接触点的接触椭圆长轴及其方向（设该方向向量为e）；

3）点Pi3、Pi4在它们接触点Pi1、Pi2处的切平面上的坐标满足式（2）和下式：

式中：R1t为接触点Pi1、Pi2处接触椭圆长轴上到点Pi1、Pi2的距离为a 的点的位置矢量；式中±分别对应点Pi3和Pi4。rpi是Pi所在的网格线上Σ1的齿高。接触点Pi1、Pi2位于预设接触路径上且对应面齿轮上的点，因此有式（8）中的第3、第4 式。联立求解式（8）和式（2）得到点Pi3、Pi4在接触点Pi1、Pi2处切平面上的坐标，记为Rti3、Rti4，对应切平面上的点ti3、ti4，如图6 所示。

图6 接触椭圆长轴与接触线的间隙δp

图6 所示为接触点Pi1、直线bi1、切平面Π、点ti3、点Pi3、Σ1与Σa的接触线L21表示在齿面Σ1上的相互之间的关系。点ti3到点Pi3的法向距离为δp。

4）点Pi3在Σ1上的齿面坐标可按式（9）求解（点Pi4与点Pi3相同）。

式中n1i1是接触点Pi1处的单位法矢，R1i3（us，θs，Ψ2）是点Pi3在Σ1上的齿面坐标。

在小轮拓扑修形齿面Σp上点Pi、Pi3、Pi4的齿面位置矢量为

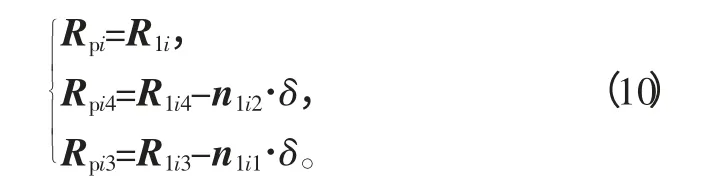
式（10）在小轮拓扑修形齿面Σp上定义了3×（2m-1）个点，通过这些点和下文的“小轮拓扑修形齿面Σp的加工”可以确定完整的齿面Σp。

5 小齿轮拓扑修形齿面的加工

5.1 小轮加工原理

由上述推导可知拓扑修形齿面Σp上接触路径P1P2m-1上的点修形量为0，而接触路径两侧的点Pi3、Pi4的修形量大于0，由图5 可以看出顶点C、D 处的齿面修形量最大，另外两个顶点E、F 处的齿面修形量最小，因此采用具有渐开线齿廓的盘形砂轮磨齿加工小轮拓扑修形齿面，如图7 所示。

图7 中坐标系Sg、Sp、Sv分别与盘形砂轮、小齿轮和插齿刀V 固联，Sn为固定坐标系，Sv与Sn间没有相对运动，St与砂轮中心固联，为辅助坐标系。rp1、rpv分别为小齿轮和插齿刀的分度圆半径。图示为某一瞬时各轮的转动状态。砂轮的齿廓由插齿刀的齿廓确定，即在xgyg平面内砂轮的工作齿面的截面与虚拟插齿刀的轴截面轮齿齿廓相同（此时Eg=0）。考虑到具有渐开线的盘形砂轮与小齿轮拓扑修形齿面Σp为点接触，在加工过程中磨损较快，因此采用大直径砂轮，减小砂轮磨损的速度。从而插齿刀的齿数多于小齿轮的齿数才能定义砂轮的工作曲面。

图7 小齿轮齿面Σp 展成加工坐标系

小齿轮绕其自身轴线zp旋转φp，盘形砂轮绕轴线zt旋转φg，转速之比为小齿轮与插齿刀的齿数之比，这两个运动即构成小轮加工的展成运动。砂轮绕其自身轴线xg做切削运动。砂轮中心做与插齿刀轴线平行的直线运动Lg，为进给运动。这样加工的小齿轮为标准渐开线齿面，不能满足啮合性能的设计要求。为了能够加工出由图5 所示构造的小轮拓扑修形齿面Σp，砂轮中心还必须在yvzv平面内做抛物线运动Eg，砂轮中心在yv方向的偏移量Eg或该抛物线的参数由齿面Σp上的点Pi3、Pi和Pi4的齿面坐标确定。因此有2m-1 条不同的抛物线，最后将这些抛物线的参数拟合为旋转φg的转角函数。

5.2 小轮齿面方程

由图7 可知通过将插齿刀v 的轴截面齿廓绕xv旋转（此时Eg=0）可得砂轮的工作齿面，设砂轮工作齿面的位矢和法矢分别为Rg（θg，θv）、ng（θg，θv），其中θg、θv为其曲面参数。

小齿轮拓扑修形齿面Σp展成加工的详细坐标系如图7 所示。设Eg的表达式如下：

式中，c1、c2和c3待确定，并可由式（12）表示。式（12）中qji（j=1，2，3，i=1…2m-1）待确定，本文采用多项式拟合确定，若要提高精度，也可用最小二乘法。

通过坐标变换导出小轮的齿面位矢为：

式中：φp=φgNv/N1，Nv、N1分别为插齿刀v 和小齿轮的齿数；M1n~tg是坐标变换矩阵。由于运动参数Lg和φg相互独立，因此啮合方程如下：

5.3 确定系数cj，qjk

据上述可知已由式（10）确定了齿面Σp在点Pi、Pi3和Pi4处的齿面坐标，由式（13）确定的小轮齿面方程包含未知数c1i~c3i，式（13）表示的小轮齿面必须过Pi3、Pi4和Pi，则有如下方程：

式中，φ1gi-3gi、L1gi-3gi是砂轮加工齿面Σp上的点Pi3、Pi和Pi4时的运动参数。上式3 个矢量方程每个有3 个分量，共9个方程和9 个未知数，因此c1i~c3i具有唯一解。

为了确定qji，例如对于cj，由上式求解出了cji，而要求解qji，可建立如下线性方程：

由于φ2gi是点Pi（修形量为0）处砂轮的运动参数，与φ1gi和φ3gi相比，误差较小，因此用φ2gi求解多项式系数qji更可取，实际上在下述计算实例中，取φ1gi和φ3gi都使上式求解不收敛。

6 计算实例

6.1 实例1

预设面齿轮传动的啮合性能为：接触路径方向θ=89.7°；接触椭圆长半轴长度a=0.15×（L2-L1）=12 mm；传动误差参数为（a1=-0.006，a2…an-1=0）。面齿轮传动的基本参数如表1 所示。

图8 Σp 与Σa 啮合的传动误差

图9 Σp 与Σa 啮合的接触印痕

小齿轮的加工规律可用qjk表示，qjk各个元素如表2所示，其中m=4。小齿轮加工参数的拟合精度如图10 所示，其中标记▽、〇、□分别为c3i、c1i和c2i的数据点，虚线、细实线和点划线是拟合曲线，这些拟合曲线都通过了对应的数据点，拟合精度较高，因此采用式（17）的拟合方法即可确定小齿轮的加工参数cj。

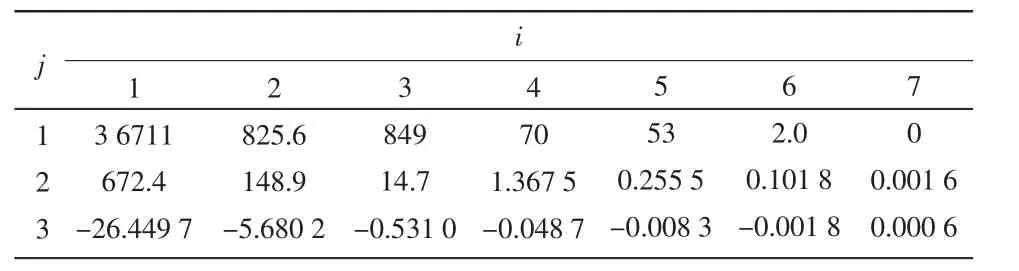
表2 小齿轮加工参数cj 的多项式系数qji

图10 小轮加工参数cj 的拟合

图11 小轮齿面Σp 相对标准渐开线齿面的修形量

图11 为小轮拓扑修形齿面Σp相对标准渐开线齿面的修形量，该修形量还包括图3 所示的齿面偏差。比较图3 和图11 可知，Σp相对标准渐开线齿面既有齿向修形，又有齿廓修形，修形量为负表示的意义是在标准渐开线齿面上去除材料。

总之小齿轮拓扑修形齿面的修形量由预设的传动误差、选定的参考点Mm、接触路径方向θ、接触椭圆的长度a 决定。

6.2 实例2

实例1 是用本文的主动设计方法设计抛物线传动误差，本文的主动设计方法还可用来设计高阶传动误差，如本实例四阶传动误差及接触路径倾斜的设计。

预设面齿轮传动的啮合性能为：接触路径方向θ=13°；接触椭圆长半轴长度a=0.2×（L2-L1）=16 mm；传动误差参数为（a1=0.000 5，a2=0，a3=-0.02，a4…an-1=0）。其它参数与表1 相同。

预设的传动误差和接触路径如图12 和图13 所示，图13 以标记的点为设计参考点。由图12 和图13 可以看出预设的啮合性能与TCA 模拟结果几乎相同。这里的参考点Mm的坐标是LMm=530 mm、rMm=-89.6 mm。接触椭圆半轴长度与预设长度的最大误差为1.35 mm，位于面齿轮的齿根，最小误差为0.71 mm，位于面齿轮的齿顶。这些结果与预设啮合性能基本一致。

图12 Σp 与Σa 啮合的传动误差

图13 Σp 与Σa 啮合的接触印痕

7 结 论

1）基于构造拓扑修形齿面的方法，提出了近似面齿轮传动的主动设计，因此齿面设计、啮合性能的控制不再局限于齿面修形技术。

2）由于小齿轮拓扑修形齿面结构的特殊性，采用局部点接触法磨齿加工，论述了该齿面的加工原理，确定了小齿轮拓扑修形齿面的加工参数，计算实例表明该加工方法是可行的。

3）通过计算实例，可以看出主动设计后Σp与Σa的啮合性能与预先给定的啮合特性能非常吻合，说明了基于齿面拓扑修形的主动设计在控制近似面齿轮传动啮合性能方面的优势。

4）需要指出的是：该方法可以主动地和定量地控制接触椭圆长度，接触印痕的位置、方向和传动误差。

［1］ 彭先龙，方宗德，苏进展，等.应用大碟形刀具加工面齿轮的理论分析［J］.哈尔滨工业大学学报，2013，45（5）：80-85.

［2］ Litvin F L，Zhang Yi.Local synthesis and tooth contact analysis of face milled spiral bevel gears［R］.Technical report 90-C-028,Washington：NASA center for aerospace information，1991.

［3］ Litvin F L，Gutman Y.Method of synthesis and analysis for hypoid bear-drives of“formate”and“helixform”［J］.Journal of mechanical design，1981，103（83）：2015-2021

［4］ Cao Xuemei，Fang Zongde，Xu Hao，et al.Design of pinion machine tool setting for spiral bevel gears by controlling contact path and transmission errors［J］.Chinese Journal of Aeronautics，2008，21（2）：179-186.

［5］ 吴训成，毛世民，吴序堂.点啮合齿面主动设计研究［J］.机械工程学报，2000，36（10）：70-73.

［6］ Shih Yipei.A novel ease-off flank modification methodology for spiral bevel and hypoid gears ［J］.Mechanism and Machine Theory,2010，45（8）：1108-1124.

［7］ Kolivand M Kahraman A.An Ease-Off Based Method for Loaded Tooth Contact Analysis of Hypoid Gears Having Local and Global Surface Deviations ［J］.Journal of Mechanical Design，2010,132（7）：1004-1013.

［8］ Litvin F L，Seol I H，Kim D，et al.Kinematic and Geometric Models of Gear Drives［J］Journal of Mechanical Design，1996，118（4）：544-550.

［9］ Lee Chengkang.Manufacturing process for a cylindrical crown gear drive with a controllable fourth order polynomial function of transmission error［J］. Journal of Materials Processing Technology，2009，209（1）：3-13.

［10］ 邓效忠.高重合度弧齿锥齿轮加工参数设计与重合度测定［J］.机械工程学报，2004，40（6）：95-99.