构造奇数3（2 m+1）阶完美幻方的方法

詹森，王辉丰

（1.广东技术师范学院计算机科学系，广东广州510665；2.海南师范大学数学与统计学院，海南海口571158）

构造奇数3（2 m+1）阶完美幻方的方法

詹森1，王辉丰2

（1.广东技术师范学院计算机科学系，广东广州510665；2.海南师范大学数学与统计学院，海南海口571158）

根据有关文献和两个幻方的加法，完整地解决了构造奇数n=3（2m+1）（m=1，2，…为自然数）阶完美幻方（包括对称完美幻方）的方法及其证明.并完整地解决了构造奇数n=2m+1（m=1，2，…为自然数）阶完美幻方（包括对称完美幻方）的问题.

奇数阶；完美幻方；对称完美幻方；余函数；基方阵；转置方阵；六步法

文[1]指出，构造奇数n=3（2m+1）（m=1，2，…为自然数）阶完美幻方一直是一个未解决的问题，文[1]解决了构造9阶（当m=1时）完美幻方或对称完美幻方的问题.要彻底解决这个问题比构造其他奇数阶幻方一直是更艰难的一个问题.文[2]解决了构造3（2m+1）（m为m≠3t+1，t=0，1，2，…的自然数）阶完美幻方或对称完美幻方的问题，对于解决上述的难题前进了一大步.然而，对于m≠3t+1，即n=32（2t+1）（t=1，2，…）时还是没有解决.由于2t+1可表示为2t+ 1=3k-2（2s+1），n=32（2t+1）=3k（2s+1），（k=2，3，4，…；s≠3d+1，d=0，1，2，…为自然数），可见，首先要对构造3k阶完美幻方进行讨论如下.

1 构造n=3k（k=3，4，…为自然数）阶完美幻方的步骤

第一步把1～27分为9个基组，每组有3个数（称为基数），其和均为42.这是很易办到的，例如如下的基组：

是一种选择.

当n=3k（k=3，4为自然数）时，把9个基组的各个基数分别加以（t-1）×27；t=1，2，…3k-3（k=3，4，…为自然数），共得大组，每个大组有9个小组，每个小组3个基数.笫t个大组，其每个小组3个基数和均为42+ 3（t-1）×27.

笫二步构造基行1，基行2和基行3.

从每一个大组任取一个小组，3k-3个大组共取出3k-3个小组3k-2个基数，随意置于基行1从左到右的第1+3（j-1）（j=1，2，…3k-2为自然数）个位置，这3k-2个基数的和为

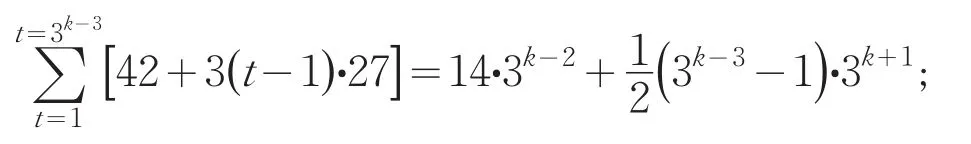
从每一个大组剩下的小组中任取一个小组，3k-3个大组共取出3k-3个小组3k-2个基数，随意置于基行1从左到右的第2+3（j-1）（j=1，2，…3k-2为自然数）个位置，这3k-2个基数的和为

从每一个大组剩下的小组中任取一个小组，3k-3个大组共取出3k-3个小组3k-2个基数，随意置于基行1从左到右的第3+3（j-1）（j=1，2，…3k-2为自然数）个位置，这3k-2个基数的和为

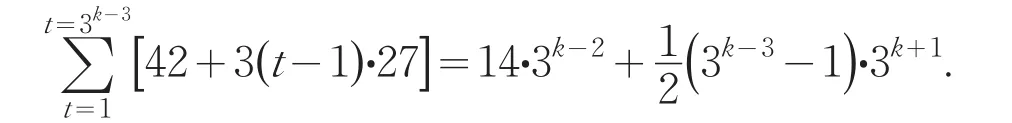
至此得基行1.这样继续下去，以同样的方式得到基行2和基行3.每个基行3k-1个基数的和为

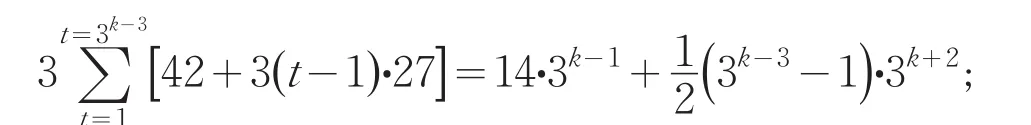
笫三步构造n=3k（k=3，4为自然数）阶基方阵A

把基行1的3k-1个基数从左到右依次记作a1，，则

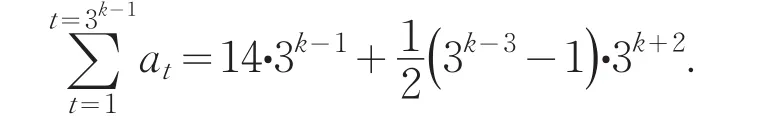
把基行2的3k-1个基数从左到右依次记作b1，b2，…，b3k-1，则

把基行3的3k-1个基数从左到右依次记作c1，，则

从左到右依次取a1，a2，…，an共三次作为基方阵A的第一行，第一行的元素向左顺移3个位置得笫二行，第二行的元素向左顺移3个位置得笫三行，依此类推直至得出笫行.

从左到右依次取c1，c2，…，共三次作为基方阵A的第行，第行的元素向左顺移3个位置得笫行，第行的元素向左顺移3个位置得笫行，依此类推直至得出笫行.

第四步作基方阵A的转置方阵B.以b（i，j）记转置方阵B位于第i行第j列的元素，有

第五步作方阵C.以c（i，j）记方阵C位于第i行第j列的元素，取

第六步基方阵A与方阵C对应元素相加所得方阵D，就是一个n=3n=3k（k=3，4为自然数）阶完美幻方（见以下定理证明）.若以d（i，j）记方阵D位于第i行第j列的元素，显然n=3k（k=3，4为自然数）阶完美幻方的6个步骤简称六步法.

以上构造n=3

2 定理及证明

证明分5步证明如下

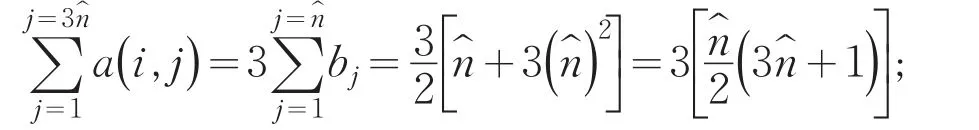
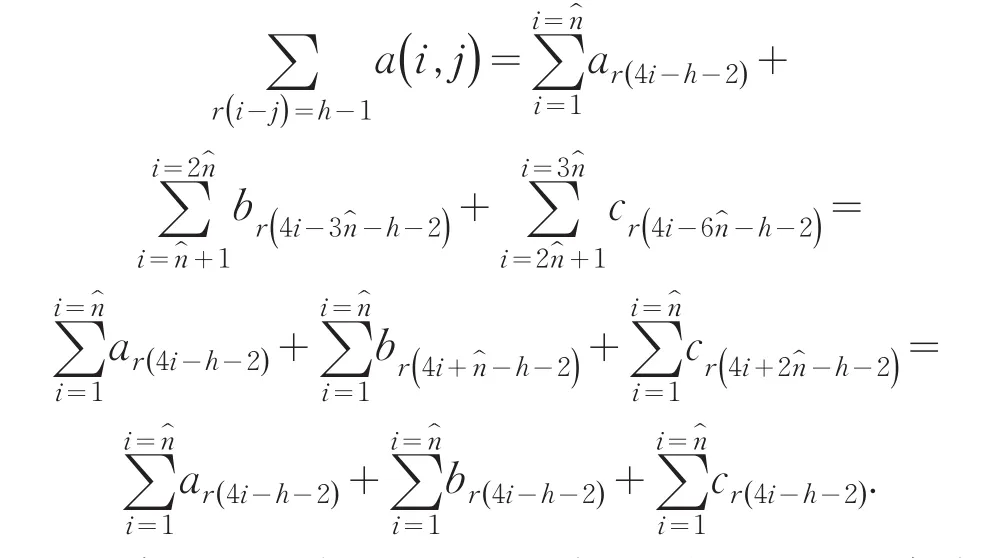
在求和过程中，-h-2是固定的，由文[3]的预备定理得

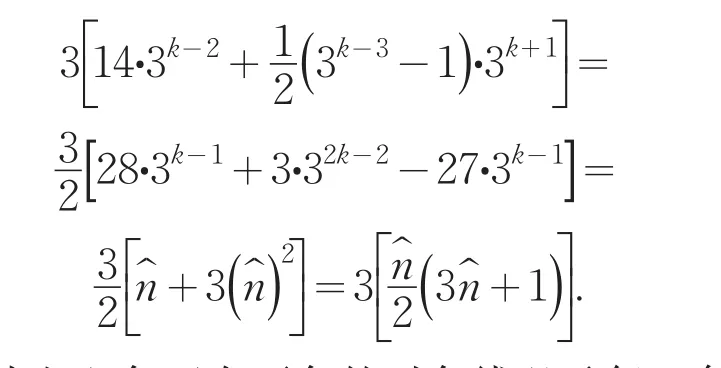
即从左上角至右下角的对角线以及每一条与其同方向的泛对角线上的元素之和都等於常数

在求和过程中，h-3是固定的，由文[3]的预备定理知

即从左下角至右上角的对角线以及每一条与其同方向的泛对角线上的元素之和都等于常数

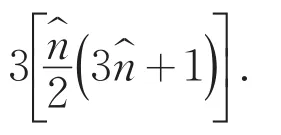
由以上事实可见，方阵A是一个非正规完美幻方，其幻方常数为

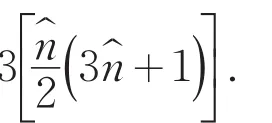
2）显然，基方阵的转置方阵A亦是一个非正规完美幻方，其幻方常数为

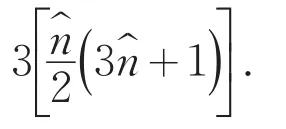
3）由于方阵C位于第i行第j列的元素

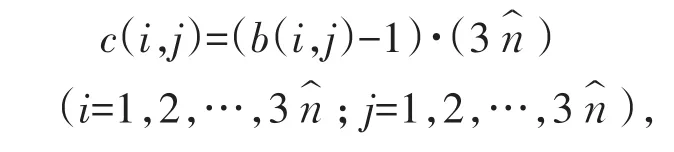
所以方阵C是一个非正规完美幻方，其幻方常数为

4）由于方阵D是由基方阵A与方阵C对应元素相加所得，故方阵D是一个完美幻方，其幻方常数为

5）最后我们还需证明方阵D是一个正规的完美幻方.

考察方阵D的元素，

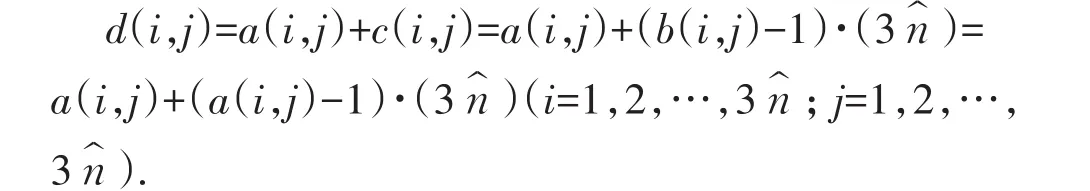
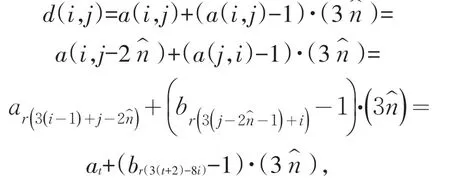
又由于六步法第二步中从每一个大组任取一个小组，3k-3个大组共取出3k-3个小组3k-2个基数，随意置于基行从左到右的第i+3（j-1）（i=1，2，…，3.i=1，2，…，3k-2为自然数）个位置，每一个基行有（（3k-2）!）3种选法，三个基行共有（（3k-2）!）9种选法.故六步法可得到个不同的为自然数）阶正规的完美幻方.

在构造n=3（kk=3，4为自然数）阶完美幻方的步骤中，只需选取a1，a2，…，an；b1，b2，…，bn；c1，c2，…，cn使方阵A为一个对称方阵，其他步骤不变就可构造出n=3（kk=3，4为自然数）阶对称完美幻方，这样实际上就是以上定理的推论（见以下推论）.

推论当a1，a2，…，an；b1，b2，…，bn；c1，c2，…，cn的选取使方阵A为一个对称方阵时，六步法得到的是一个n=3（kk=3，4为自然数）阶正规的对称完美幻方.

选取a1，a2，…，an；b1，b2，…，bn；c1，c2，…，cn使方阵A为一个对称方阵的方法如下：由另一种选择把1～27分为9个基组如下

（注意，基组（2）与（1）不完全相同，而上述定理的证明与基组的选择无关）

把基组（2）的各个基数分别加以（t-1）×27；t=1，2，…3k-3；k=3，4，…为自然数），共得3k-3大组.为确保方阵的中间一行对称，将中间行称为主基行I.（2）的笫二行3个基组的基数置于主基行I，笫一行3个基组的基数置于主基行II（指中间行之上一行），笫三行3个基组的基数置于主基行III（指之下一行），得

（注意，上述三行是中心对称的）.

各主基行之基组的各个基数分别加以（t-1）×27后仍在该主基行上且相对位置不变，显然，三个主基行仍是中心对称的.

3 构造奇数3（2m+1）阶完美幻方的方法

文[3]给出了构造m=2m+1（m为m≠3t+1，t=0，1，2，…的自然数）阶完美幻方或对称完美幻方的方法，以上给出了构造n=3（kk=3，4为自然数）阶完美幻方或对称完美幻方的方法，文[1]解决了构造9阶（当m=1时）完美幻方或对称完美幻方的问题.在此基础上，就可得到

定理2设A，B分别为3（kk=2，3，4）阶，m=2m+1（m为m≠3t+1，t=0，1，2，…的自然数）阶完美幻方或对称完美幻方，则A⊕B为奇数3（k2m+1）（k=2，3，4）阶完美幻方或对称完美幻方.

根据文[4]两个幻方的加法知，两个完美或对称完美幻方的和（幻方）也是完美或对称完美幻方.所（k=3，4为自然数）阶正规的对称完美幻方.

例构造一个33阶对称完美幻方.

由以上主基行（3）计算得基行为

再根据以上六步法经过6个步骤（略）可构造出27阶对称完美幻方为以A⊕B是n=2m+1（m为m≠3t+1，t=0，1，2，…的自然数）阶完美或对称完美幻方.

由于n=2m+1（m=1，2，3，…）中出现3的倍数（即m=3t+1）时，这时，又可把n=2m+1表示3k（2m+1）的形式，再根据文[4]加法知A⊕B为奇数3k（2m+1）（k= 2，3，4）阶完美幻方或对称完美幻方.

综上可见，构造奇数n=3（2m+1）（m=1，2，…为自然数）阶完美幻方或对称完美幻方的问题就从理论和实际上得到了解决，从而构造所有奇数阶完美幻方或对称完美幻方的问题也就从理论和实际上得到了解决.由此可见，以上构造3k（k=3，4，…为自然数）阶完美幻方或对称完美幻方的方法，对于解决构造奇数n=3（2m+1）（m=1，2，…为自然数）阶完美幻方或对称完美幻方的难题起着决定性的作用.

[1]詹森.关于构造k2阶完美幻方的方法[J].海南师范大学学报：自然科学版,2012,25(2)：147-157.

[2]詹森,王辉丰.构造3n阶完美幻方的五步法[J].海南师范大学学报：自然科学版,2014,27(1)：18-22.

[3]詹森,王辉丰.构造奇数阶幻方,完美幻方和对称完美幻方的新方法[J].海南师范大学学报：自然科学版,2011,24(3)：265-269.

[4]詹森,王辉丰.关于构造高阶幻方的新方法[J].海南师范大学学报：自然科学版,2009,22(3)：250-254.

责任编辑：黄澜

The Structure Method about 3（2m+1）Order Perfect Magic Square

ZHAN Sen1，WANG Huifeng2
（1.Department of Computer Science，Guangdong Technical Normal University，Guangzhou 510665，China；2.College of Mathematics and Statistics，Hainan Normal University，Haikou 571158，China）

By using the exisiting research results and the results in this paper,according to two magic square addition,the problem about structuring n=3（2m+1）（m=1，2，…is natural number）order perfect magic square（including symmetric per⁃fect magic square）was completely solved,the method and its theoretical proof was given.And the problem of structuring any odd-order perfect magic square（including symmetric perfect magic square）was also solved.

Odd-order；perfect magic square；symmetry perfect magic square；residual function；Base matrix；Transpose matrix；six footwork method

O 157.6

A 文章编号：1674-4942（2014）02-0133-05

2014-01-28