仿真混凝土不同龄期单轴动态压缩全曲线试验研究

张 宇，冯 新，周 晶，邹 浩，朱 昆

（大连理工大学海岸及近海工程国家重点实验室，辽宁大连116024）

仿真混凝土不同龄期单轴动态压缩全曲线试验研究

张 宇，冯 新，周 晶，邹 浩，朱 昆

（大连理工大学海岸及近海工程国家重点实验室，辽宁大连116024）

通过系列试验研究仿真混凝土动态受压特性，为高坝模型动力试验提供相关材料参数。在应变速率范围内对5种不同养护时间的仿真混凝土试块进行单轴压缩试验研究。通过试验得到仿真混凝土单轴受压应力－应变全曲线，建立曲线基本方程，分析关键龄期范围内峰值应力、峰值应力处应变、弹性模量的率相关性，对动态抗压强度、弹性模量分别给出反映应变率影响的经验公式。通过与混凝土率相关特性以及破坏形态的对比，得出结论：仿真混凝土单轴受压特性在弹性阶段和非弹性阶段都与混凝土具有相似性，适合用于研究混凝土坝动力损伤或者破坏阶段模型试验。

仿真混凝土；动力特性；全曲线；龄期影响；单轴压缩

我国大江大河的源头和水能资源集中在西部高山崇岭的陡峻河谷中，地形地质条件适宜修建高坝水库。西部地区是我国主要地震区，地震的强度和发震频率都很高。高坝的抗震安全一直是一个必须面对和急需解决的关键技术问题，当前特别是对高拱坝的抗震安全，尤为迫切［1］。混凝土高坝地震反应预测主要依靠数值模型，这不可避免的简化或近似采用很多参数，数据的缺乏使得核实数值计算结果非常困难，这就需要进行一定规模的试验，从试验角度来研究高坝地震反应问题。

依据相似理论基本定理，混凝土坝模型动力破坏试验需要满足相似条件的要求。具体来说，试验对材料的密度、弹性模量、不同加载速率下的应力应变全曲线、泊松比等材料参数有较为苛刻的要求。近几十年来，国内外很多学者对混凝土坝模型材料进行了研究。léger P等［2－3］以石膏为主要材料制作模型进行动力模型试验，然而石膏材料本身密度较低，虽然可以加入铅粉等改变材料密度，但又影响模型的均匀性，且石膏材料对环境温度和湿度非常敏感，与混凝土的力学性能相差较大，作为混凝土坝模型试验的材料有诸多的限制。陈厚群等［4］采用橡胶制作混凝土坝模型研究结构的动力特性，此种材料可用来确定结构频率、振型以及弹性阶段反应，有较强的非线性特性，不适用于破坏阶段试验，现已很少使用。宫必宁［5］采用矾土水泥、铁粉、水、机油等制作模型研究动水压力，材料的力学性能分别在线弹性段和塑性段与混凝土材料相似。盛志刚［6］采用重晶石膨润土混合料制作模型研究拱坝动力响应，此种材料强度较低，但泊松比和动弹模较大，很难满足弹性－重力相似关系。王海波等［7－8］选用硫酸钡、氧化铅及滑石粉为主的混合原料制作模型，材料强度较低，但模型几何比尺、密度比尺、动弹模比尺三者之间的关系亦没有严格满足弹性 －重力相似关系。

大连理工大学工程抗震研究所采用重晶石砂、重晶石粉、水泥、矿石粉等配制仿真混凝土材料用于混凝土高坝模型振动台试验，该材料具有强度低、弹性模量低、密度高、硬化快特点［9－10］。由于仿真混凝土具有早强性，强度、峰值应力处应变、弹性模量等材料参数在关键龄期范围内变化较大 ，范书立［11］研究了在龄期单因素影响下材料的静态弹模、抗压强度以及峰值应变的变化规律，并且结合模型试验受力破坏特点，研究了在应变速率单因素影响下仿真混凝土抗压强度和抗拉强度的变化规律。

本文针对不同龄期不同应变速率下仿真混凝土材料单轴受压本构关系进行了一系列的试验研究，得到此种材料在动力作用下的压应力－应变全曲线。通过对曲线特点研究，建立受压全曲线基本方程，确定振动台关键龄期范围内不同应变速率下材料的受压曲线参数值，同时分析了材料的极限抗压强度、峰值应力处应变、弹性模量与应变速率的关系，为接下来高坝模型振动台试验提供仿真材料受压特性的试验基础。

1 试验设备与实验技术

1.1 试验设备

本试验加载设备采用大连理工大学海岸与近海工程国家重点实验室的CMT5000电子材料试验机，如图1。该试验机为双工作间平台，伺服电机驱动，并配有全数字闭环测控系统和试验软件 POWERTEST。最大试验力100 kN；位移速率调整范围0.001mm／min～500 mm／min；大变形测量范围10 mm～800mm；大变形分辨力0.008mm；采样速率50次／秒；位移分辨率0.025μm。

图1 试验装置图

1.2 试件制备

本试验中采用边长为100mm的立方体试块进行动态抗压测试。为了使高坝模型动力破坏试验满足弹性－重力相似关系［12］，要求模型材料的设计强度较低，与原型混凝土的强度比尺等于两种材料的动弹模比尺。同时为使模型惯性力较大易于破坏，要求材料密度较大。仿真混凝土材料密度约为3 050 kg／m3～3 100 kg／m3。仿真混凝土材料是由矿石粉、水泥、重晶石砂、重晶石粉、河砂、水按照一定配比混合而成，具体配比见表1。其中，重晶石粉和重晶石砂均为高密市汇宝矿石工贸有限公司生产，重晶石砂为连续粒级，粒径范围为0.6 mm～2.0 mm；矿石粉和水泥均为大连小野田水泥厂生产，水泥为同炉生产的PC32.5复合硅酸盐水泥；砂子为天然河砂，平均粒径为0.5mm以上的粗砂；试块用钢模成型，振捣密实后放入温度为20±4℃、相对湿度为90%的养护室养护至龄期。

1.3 试验过程

试验过程有3个步骤：（1）将试块放在加载设备上，调整试块使其物理对中，然后调整加载头位置，使其所在平面与试块的受压面保持平行，避免偏心受压。在试块受压表面放置一块尺寸相同的薄钢块，并在试块与薄钢块之间涂抹一层润滑油，以减小薄钢块侧向约束效应对试验结果的影响。（2）通过计算机控制进行预加载。（3）选定加载速率，确定加载方案，正式加载。

表1 仿真混凝土材料配合比例（按重量）

2 试验结果与分析

考虑振动台动力作用下高坝模型结构响应的应变速率，仿真材料单轴压缩试验应变速率选为10－5／s、10－4／s、10－3／s、10－2／s，其中10－5／s为拟静态应变速率。考虑振动台模型试验需要满足相似关系中有关强度的要求，而仿真材料养护时间对强度影响很大，试块养护时间选为24 h、48 h、72 h、96 h、120 h。本次仿真材料单轴受压材料试验共进行了20组，每组4个试块进行试验测试。

2.1 应力应变全曲线

建立仿真材料受压应力－应变全曲线是研究与分析混凝土坝模型振动台试验主要材料性质的依据。图2为仿真混凝土材料在龄期24 h加载速率下单轴受压应力－应变归一化曲线，并且和过镇海等［13］给出的C20混凝土单轴受压曲线进行了对比。

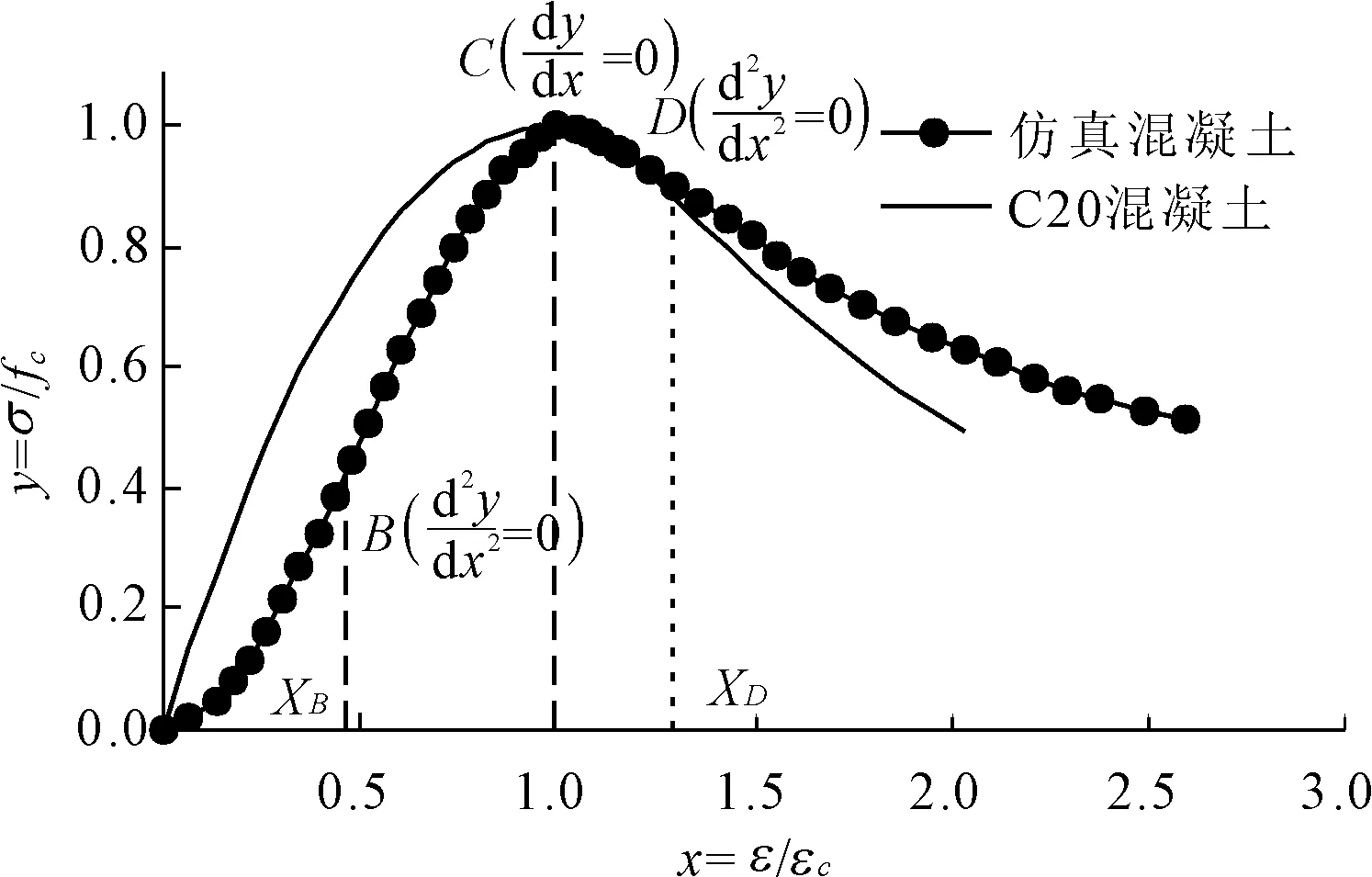
图2 仿真材料和混凝土无量纲化单轴受压应力－应变全曲线

图2反映了仿真混凝土材料单轴受压后的变形、裂纹形成与发展直到破坏的全过程特征。仿真材料实际试验测试的应力－应变全曲线采用无量纲的坐标表示：

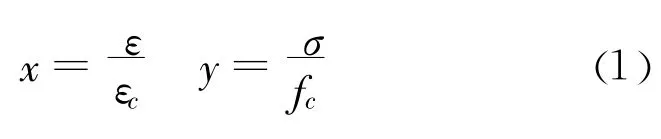
式中：ε为压应变；εc为单轴抗压极限强度fc相应的峰值压应变；σ为压应力；fc为仿真材料单轴抗压极限强度。

从图2中可以清楚的看出，仿真材料受压应力－应变全曲线上升段有拐点（B点），即x＝xB时，上升段曲线有一个拐点，而混凝土材料受压应力 －应变全曲线的上升段曲线的斜率单调减小，无拐点。参考文献［13］，根据仿真材料上升段和下降段曲线的形状，分别用多项式和有理分式进行拟合。则仿真材料受压应力 －应变全曲线的基本方程为：

x≤1时，

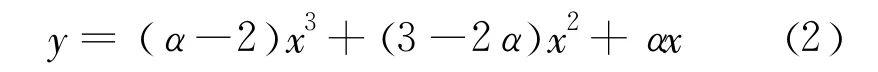
x＞1时，

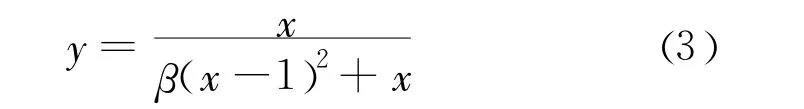
式中上升段只剩下参数α。

考虑到曲线上升段有拐点 B，可求得参数α的范围：

式（4）的范围有别于文献［13］和相关混凝土规范［14］中关于混凝土材料参数的范围，主要是因为两种材料特性的区别。仿真材料上升段的理论曲线随参数α的变化如图3所示。若α＞1.5，则曲线上升段无拐点；若α＜0，曲线局部出现y＜0，不符合试验结果。式（3）中下降段只剩下参数β，从图3中可以看出随着β值增大，下降段曲线下降速度越快。

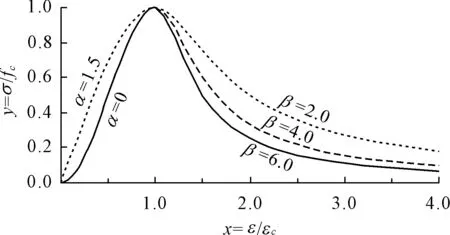
图3 考虑参数影响的单轴受压应力 －应变全曲线

此外，考虑到x＝xB时，则：

可求出上升段拐点的位置 xB。

考虑到下降段曲线上有一个拐点（D点），即 x＝ xD时，则：

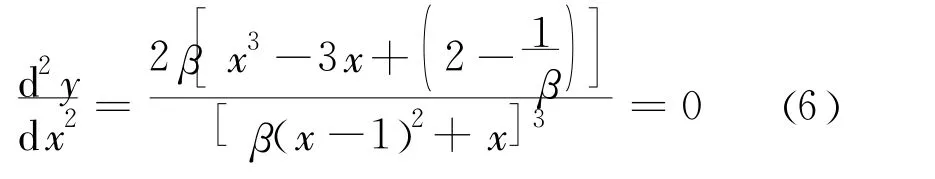
可求出下降段拐点 xD的位置。

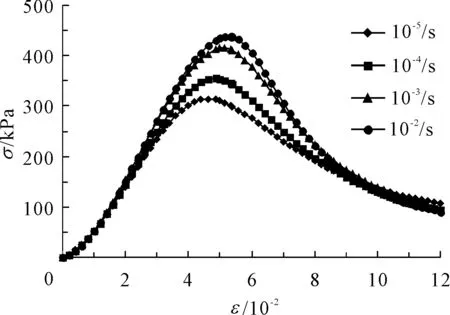
图4 24 h不同应变速率下应力－应变均值曲线

仿真混凝土材料养护24 h后实测的不同应变速率下的应力－应变均值曲线如图4所示。从图4中可清楚地看到当应变速率从 10－5／s增长到10－2／s时，应力－应变全曲线形状相似，峰值应力增长很快，峰值应变也有一定的增长，这一结论与混凝土在不同加载速率下受压试验的相关研究［15－16］结论相近。在上升段的相同应力时，高应变速率加载下的仿真材料弹性模量增大，应变值减小，曲线的上升段更加陡峭，上升段参数α值相对更小。随着加载速率的增加，曲线峰值部分趋于陡峭，曲线下降段的相对面积不断减少，仿真材料脆性破坏的特征愈发明显。当仿真材料的应力－应变全曲线下降段上应力减至峰值应力的0.5倍时，对应的压应变为εu。试验过程中注意到，当曲线下降段的应变超过εu后，由于试块的损伤已很严重，裂纹发展规律随机性增强，加载速率对曲线规律影响不明显，这与文献［17］中给出的有关混凝土率相关性试验规律相近。笔者认为，仿真材料模型结构分析中，单轴受压应变不宜超过εu。εu值可通过式（7）求得：

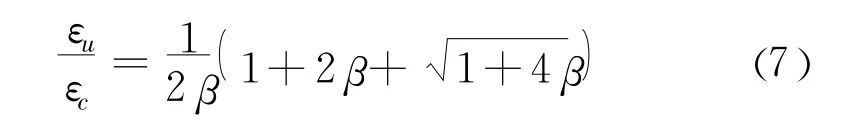
2.2 极限抗压强度

表2为试验中不同龄期不同应变速率下仿真材料极限抗压强度值。由表2可知，仿真材料极限抗压强度随着龄期和应变速率的增加而显著增加，参考文献［18］定义关于仿真材料在不同加载速率下的动力提高系数（dynamic increase factor，DIF）：

式中：fd为动力加载条件下对应的峰值应力，文中对应的应变速率分别为10－4／s、10－3／s、10－2／s；fs为拟静力加载条件下对应的峰值应力，文中对应的应变速率为10－5／s。

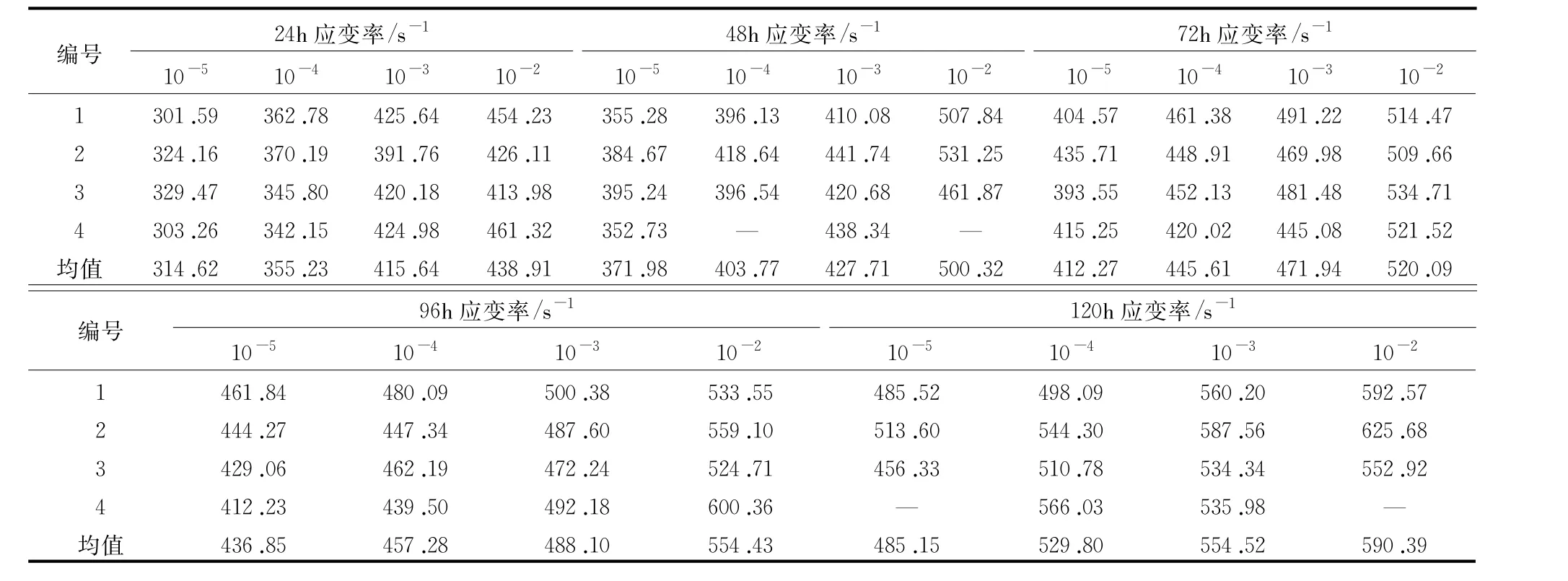
表2 不同龄期不同应变速率下的仿真材料极限抗压强度 单位：kPa

实际测试不同龄期下仿真材料强度提高系数随应变速率变化的关系如图5所示。从图5中可以看出不同龄期（24 h～120 h）范围内，仿真材料的极限抗压强度在各应变速率下都有较大的变化。随着龄期的增长，材料单轴抗压强度的率相关性有减弱的趋势，这可能是由于随着龄期增长，材料弹性模量提高，受压变形能力变弱，吸能能力减弱造成的，亦可能是由于分析数据数量的局限性造成了判断误差。

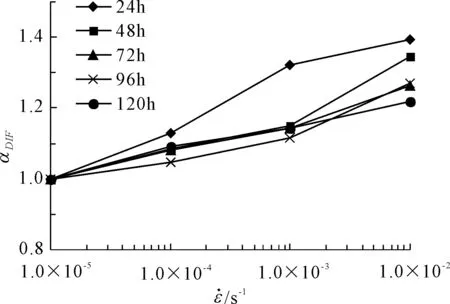
图5 不同龄期强度提高系数随应变速率的变化关系

同一龄期中材料强度的比值与应变速率比值的对数之间接近线性关系，用下面形式的方程来描述：

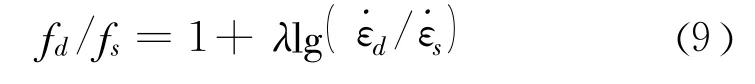
式中：˙εd为仿真材料在某一龄期对应的应变速率，取10－4／s、10－3／s、10－2／s；fd为˙εd对应的单轴受压极限强度；˙εs为仿真材料的拟静态应变速率 ，取10－5／s；fs为当前龄期˙εs对应的单轴极限抗压强度；λ为仿真材料的材料参数，通过试验数据拟合得到。龄期24 h时，λ取0.139，R2取0.975；龄期48 h时，λ取0.101，R2取0.926。

2.3 峰值应力处应变

仿真混凝土材料将用于制作坝体模型，需养护24 h至48 h然后进行振动台破坏试验，此时材料的强度特性满足相似理论。表3给出了影响振动台试验的关键龄期范围内不同应变速率下的仿真材料峰值应力处的应变值。从表3中可以看出，仿真混凝土材料峰值应力处对应的应变值随着应变速率的增加略有增大。文献［19］对混凝土材料进行相关研究也得到了类似地结论。

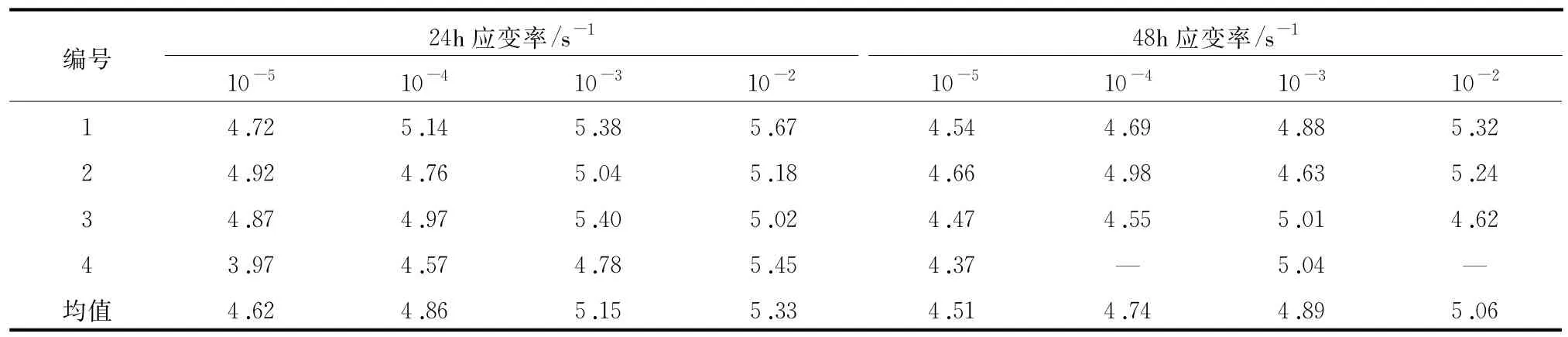
表3 不同龄期不同应变速率下峰值应力处的应变值（10－2）

2.4 全曲线参数值

把上升段参数 α、下降段参数 β、εu／εc、极限抗压强度及其对应的应变代入式（1）、式（2）和式（3），即可得到仿真材料单轴受压应力－应变全曲线。通过前期的材料试验得到以下参数值，见表4。仿真材料在关键龄期24 h～48 h内任一时间点单轴受压曲线可通过线性插值得到，为高坝模型动力试验提供材料参数。

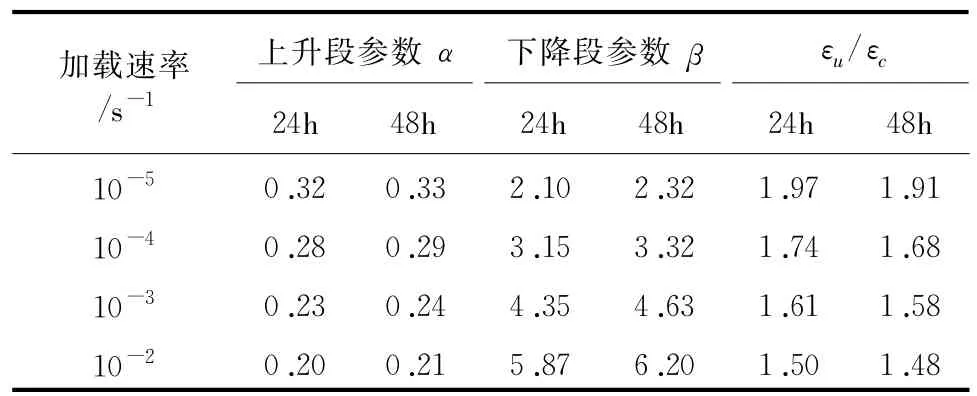
表4 不同龄期不同应变速率下单轴受压应力－应变曲线参数值

2.5 弹性模量

试验过程中，仿真材料应力应变曲线初始点的切线弹模测试难度大。本文将试验测得的应力应变曲线上达到峰值应力30%处的割线弹模作为仿真混凝土材料的弹性模量，见表5。从表5中知道，仿真材料割线模量随应变速率的增加而增大，且随着养护龄期增长，割线模量亦有所增大。同一龄期中仿真材料割线模量的比值与应变速率比值的对数之间接近线性的关系，用下面形式的方程来描述：

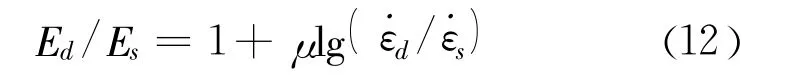
式中：˙εd为仿真材料在某一龄期对应的应变速率，取10－4／s、10－3／s、10－2／s；Ed为˙εd对应的割线模量；˙εs为仿真材料的拟静态应变速率 ，取10－5／s；Es为当前龄期˙εs对应的割线模量；μ为仿真材料的材料参数，通过试验数据拟合得到。龄期24 h时，μ取0.062，R2取0.949；龄期48 h时，μ取0.057，R2取0.906。

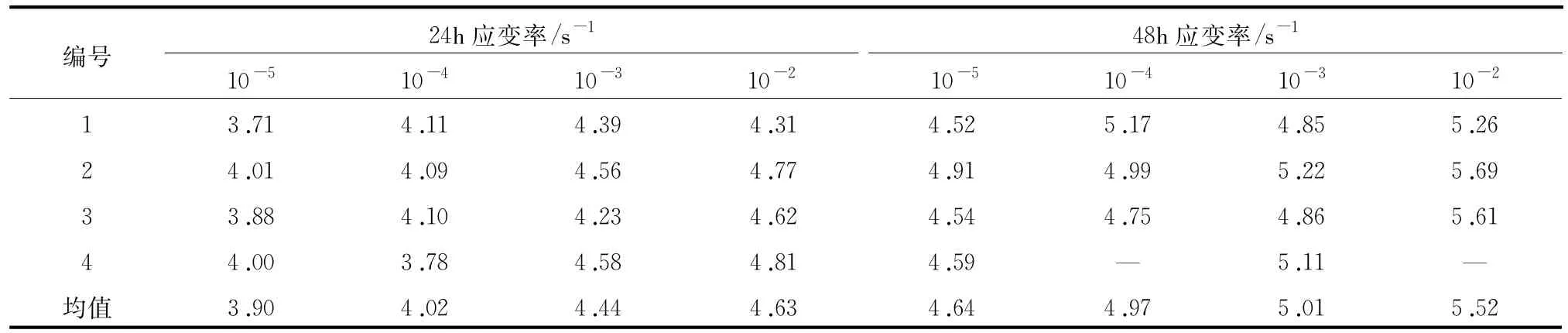
表5 不同龄期不同应变速率下的割线模量 单位：MPa

2.6 破坏形态

仿真混凝土试块加载后，竖直方向发生压缩变形，水平方向发生拉伸变形。试块的上下受压面因为承压钢板的摩擦阻力作用变形较小，试块中部水平方向的拉伸变形较大。当试块内水平向拉应力超过仿真混凝土材料的极限拉应力后，试块内将产生裂纹。试块初裂纹的出现靠近材料表层，试块中部的裂纹为竖直向，沿着斜向向上、下发展，见图6（a）。随着加载的过程裂纹发展到试块承压面的角部，形成类似的正倒方向的“八”字形，见图6（b）。继续对试块加载，裂纹开始由试块表层向内部扩展，表层的仿真混凝土材料开始鼓凸，并出现剥落，见图6（c）。仿真混凝土材料试块在单轴受压试验中，材料从裂纹的产生到破坏的形态与混凝土材料十分相似，这一点也体现了仿真材料适合用于混凝土坝缩尺模型材料的优越性。

图6 仿真材料试块在不同应力阶段的裂纹发展与破坏情况

3 结 语

（1）仿真混凝土材料单轴极限抗压强度随着应变速率和龄期的增长而提高，在同一龄期内，极限抗压强度与应变速率的对数近似为线性关系。混凝土材料单轴抗压强度也有近似的率相关性。

（2）仿真混凝土材料不同龄期不同加载速率下得到的受压应力－应变全曲线具有很好的相似性，可通过一组方程来确定，该方程中具体参数通过一系列试块试验来确定。全曲线形状与混凝土材料受压全曲线形状近似，只是仿真混凝土材料在曲线上升段存在拐点，与混凝土略有不同。

（3）仿真混凝土材料弹性模量和峰值应力处的应变随着加载速率和龄期的增长而提高，此规律与混凝土材料相关研究结果一致或近似。

（4）仿真混凝土材料立方体试块单轴受压，产生裂纹直至破坏的形态与混凝土材料十分相似。

（5）综上所述，笔者认为仿真混凝土材料单轴受压与混凝土材料在弹性阶段和非弹性阶段有很好的相似关系，适合用于研究混凝土坝动力损伤或者破坏阶段的模型试验。

［1］ 陈厚群.水工混凝土结构抗震研究进展的回顾和展望［J］.中国水利水电科学研究院学报，2008，6（4）：245－257.

［2］ Morin PB，Léger P，TinawiR.Seismic behaviorof post－tensioned gravity dams：shake table experiments and numerical simulations［J］.Journal of Structural Engineering，2002，128（2）：140－152.

［3］ TinawiR，Léger P，LeclercM，etal.Seismic safety ofgravity dams：from shake table experiments to numerical analyses［J］.Journal of Structural Engineering，2000，126（4）：518－529.

［4］ 陈厚群，唐继儒，钱维栎，等.枫树坝坝内式厂房段的动力特性和地震反应［J］.水利学报 ，1980，（2）：34－43.

［5］ 宫必宁.重力坝地震动水压力试验研究［J］.河海大学学报，1997，25（1）：98－102.

［6］ 盛志刚，徐艳杰，刘海笑.拱坝横缝配筋动力响应的模型试验和计算分析［J］.清华大学学报：自然科学版，2009，49（3）：317－320.

［7］ Wang Haibo，Li Deyu.Experimental study of seismic overloading of large arch dam［J］.Earthquake Engineering and Structural Dynamics，2006，35（2）：199－216.

［8］ Wang Haibo，LiDeyu.Experimental study of dynamic damageof an arch dam［J］.Earthquake Engineering and Struc－tural Dynamics，2007，36（3）：347－366.

［9］ Lin Gao，Zhou Jing，Fan Chuiyi.Dynamicmodel rupture test and safety evaluation of concretegravity dams［J］.Dam Engineering，1993，4（3）：769－786.

［10］ 朱 彤，林 皋，马恒春.混凝土仿真材料及其应用的试验研究［J］.水利发电学报，2004，23（4）：31－37.

［11］ 范书立.混凝土重力坝的动力模型破坏试验及可靠性研究［D］.大连：大连理工大学，2007.

［12］ 林 皋，朱 彤 ，林 蓓.结构动力模型试验的相似技巧［J］.大连理工大学学报 ，2000，40（1）：1－8.

［13］ 过镇海，张秀琴，张达成，等.混凝土应力－应变全曲线的试验研究［J］.建筑结构学报，1982，3（1）：1－12.

［14］ 中华人民共和国建设部.GB50010－2002.混凝土结构设计规范［S］.北京：中国建筑工业出版社，2002.

［15］ Rostasy FS，Hartwich K.Compressive strength and deformation of steel fibre reinforced concrete under high rate of strain［J］.International Journal of Cement Composites and LightweightConcrete，1985，7（1）：21－28.

［16］ Ahmad SH，Shah SP.Behaviourof hoop confined concrete under high strain rates［J］.ACIJournal，1985，82（5）：634－637.

［17］ 曾莎梦，李 杰.混凝土单轴受压动力全曲线试验研究［J］.同济大学学报：自然科学版，2013，41（1）：7－10.

［18］ Biscoff PH，Perry SH.Compression behaviour of concrete athigh strain rates［J］.Material and Structures，1991，24（6）：425－450.

［19］ 闫东明.混凝土动态力学性能试验与理论研究［D］.大连：大连理工大学，2006.

Experimental Study on Uniaxial Compression Behavior of Simulated Concrete under Dynam ic Loading at Different Ages

ZHANG Yu，FENG Xin，ZHOU Jing，ZOU Hao，ZHU Kun
（State Key Laboratory of Coastal and Offshore Engineering，Dalian University of Technology，Dalian，Liaoning 116024，China）

This research tries to provide the relevantmaterial parameters for the dynamic teston high dam models based on the experiments of dynamic compression characteristics of simulated concretematerials.Uniaxial compression tests on simulated concrete blocks at 5 differentageswere carried outat different loading rateswithin range.Based on the tests，uniaxial compressive stress－strain curvewas obtained and the basic equation for the curvewas established.In addition，the strain－rate－dependent characteristicsof peak stress，strain atpeak stress and the elasticmodulus at the key ageswere analyzed.Furthermore，Empirical formulas reflecting effects of dynamic compressive strength and elasticmodulus on the strain ratewere also established respectively.Comparison between the strain－rate－dependent characteristics and concrete failure patterns leads to the conclusion that the uniaxial compression of simulated concretematerials is similar to real concrete atboth the elastic stage and inelastic stage，thus applicable to studiesofmodel testsof concrete dams at the dynamic damage stage or the failure stage.

simulated concrete；dynamic characteristics；fully stress－strain curve；age effect；uniaxial compression

TU528.59

A

1672—1144（2014）04—0077—07

10.3969／j.issn.1672－1144.2014.04.014

2014－02－22

2014－03－24

973课题“高碾压混凝土坝全寿命周期性评估和安全控制”（2013CB035906）

张 宇（1984—），男 ，黑龙江省大庆人 ，博士研究生，研究方向为高坝模型动力破坏试验与数值研究。

冯 新（1971—），男 ，河南省商丘人 ，教授，博士生导师 ，主要从事结构抗震理论及实验技术研究。