土体强度参数对边坡隧道影响数值模拟分析

刘志伟

(国网福建省电力有限公司 经济技术研究院，福建 福州350012)

目前，我国大力发展隧道工程建设，主要为加快城市间公路和铁路修建，提高国民经济发展。而边坡工程与隧道工程又有着密不可分的联系。因此，结合二者共同分析研究，可为类似实际工程提供建设性与可行性建议。

在边坡隧道稳定性分析中，土体强度参数对计算结果起着至关重要的作用[1]。王毅[2]对比分析线性和非线性强度参数对边坡稳定性的影响程度，通过实例分析得出，抗剪强度参数选取关系到分析结果的正确性。陈科平等学者[3]采用极限平衡法分析边坡强度参数对其稳定性影响。姜彤等学者[4]认为抗剪强度参数之间具有一定相关性，从而，对其取值的概率分布从边坡可靠度角度进行了分析。李宗坤，杨艳荣[5]编制C++程序，结合河南省某水库边坡工程，分析土体强度参数统计特性对其可靠性影响。目前，大量学者[5－14]在强度参数对边坡稳定性的影响方面做了详细地研究。因此，本文以一典型土质边坡为例，着重研究隧道轴线与滑动方向相互垂直的情况下，不同抗剪强度参数对边坡隧道的扰动影响，为此类边坡隧道建设提供可行性参考。

1 有限元计算

1.1 边坡概况

该边坡位于某建设中的高速路旁。边坡高50 m，坡脚45°，欲开挖的隧道轴线与边坡的滑动方向相互垂直，隧道的最大跨径12 m，洞顶距坡面竖向距离为15 m，采用厚度为0.15 m的衬砌进行支护，如图1所示。土体按莫尔－库仑理想弹塑性材料考虑，其重度 γ =16 kN/m3，弹性模量 E=500 MPa，泊松比μ=0.32。衬砌按照弹性材料考虑，其弹性模量E=19 GPa，泊松比μ=0.2。仅考虑土体自重，不计其他外荷载对结果的影响。

图1 边坡隧道示意图(单位:m)

1.2 模型建立

本文将整个边坡简化为二维平面应变问题处理。土体和衬砌均采用实体单元模拟，网格划分均采用三节点平面应变单元(CPE3)。边坡两侧采用水平约束，底部施加竖向约束和水平约束。同时，采用了多点约束(MPC)的方法，将衬砌和隧道两个独立的部分，加以适当的约束，使得衬砌和隧道边界上的节点具有相同度。为了保证计算的精度，对衬砌和隧道附近适当加密网格，有限元网格如图2所示。

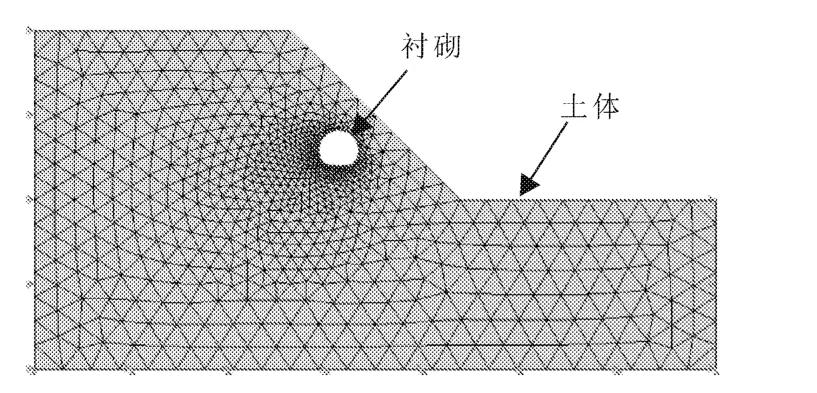
图2 边坡隧道二维有限元网格

1.3 建模步骤[15]

Step1:地应力平衡，消除初始应力产生的位移对结果的影响。

Step2:隧道的开挖过程主要是边坡内部应力释放的过程，应将开挖区单元弹性模量降低40%，来模拟应力释放的过程[16];

Step3:激活衬砌单元;

Step4:移除开挖区单元，完成隧道开挖模拟。

2 结果分析

2.1 考虑粘聚力C对边坡位移的影响

现取土体弹性模量E=500 MPa，内摩擦角φ=30°，剪胀角 ψ =28°。分别选取 c=15 kPa，16 kPa，17 kPa，18 kPa，19 kPa，20 kPa，25 kPa，30 kPa 以及40 kPa九种情况下，研究不同粘聚力c对边坡位移的影响。

受篇幅限制，仅列出 c=15 kPa，20 kPa，25 kPa和40 kPa四种典型情况下对应的位移等值云图，如图3～图6所示。

图3显示出粘聚力c=15 kPa时边坡竖向位移等值云图。由图3可知，最大下滑位移为18.6 cm，坡面最大隆起位移近似14.6 cm。坡顶和坡脚附近产生最大位移，并未对隧道产生较大的扰动。笔者认为，若土体具有较小的强度参数，将导致边坡本身失稳破坏，并未因隧道开挖而引起破坏。

图3 粘聚力c=15 kPa竖向位移等值云图

图4 表示为粘聚力c=20 kPa时边坡竖向位移等值云图。对比图3和图4发现，最大下滑位移和最大隆起位移均减小了近4倍。说明，在此范围内，粘聚力c值对边坡位移产生显著波动。

图4 粘聚力c=20 kPa竖向位移等值云图

图5 为粘聚力c=25 kPa时边坡竖向位移等值云图。随后粘聚力c逐渐增长，最大下滑位移减小到2.2 cm，最大隆起位移约为1.9 cm。对比图4和图5可知，边坡位移变化幅值在合理区间内，整个边坡隧道趋于稳定。

图5 粘聚力c=25 kPa竖向位移等值云图

图6 所示为粘聚力c取最大值40 kPa时竖向位移等值云图。比较图5与图6，可以看出，即便粘聚力c显著增大，边坡竖向位移均未发生较大变化。表明，超过一定范围后，粘聚力c的取值对边坡位移变化将不会再产生实质性的影响。

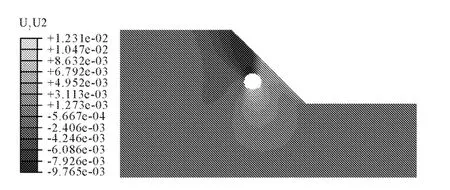
图6 粘聚力c=40 kPa竖向位移等值云图

在其他参数保持不变的基础上，弹性模量E=500 MPa和E=800 MPa两种情况下，不同粘聚力c值下的边坡最大位移量，见表1。其关系曲线见图7和图8所示。

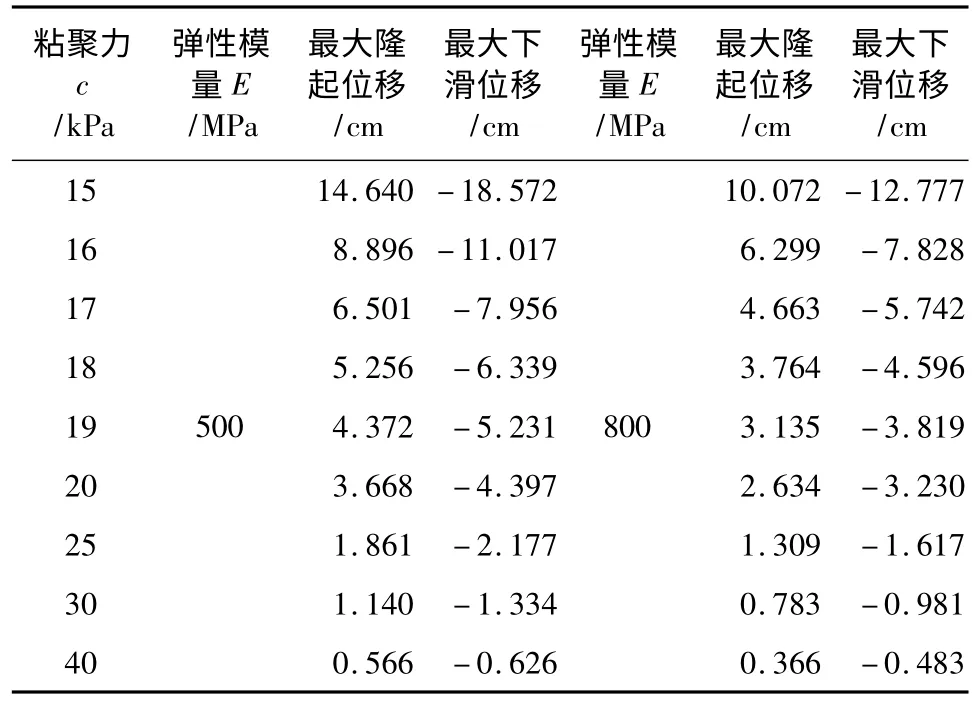
表1 不同粘聚力下坡面最大位移

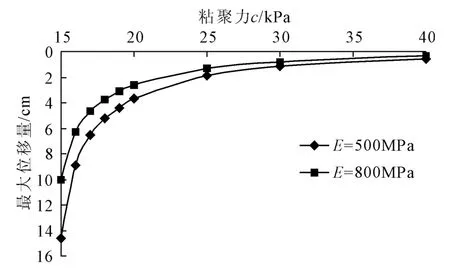
图7 不同粘聚力c下坡面最大隆起位移曲线

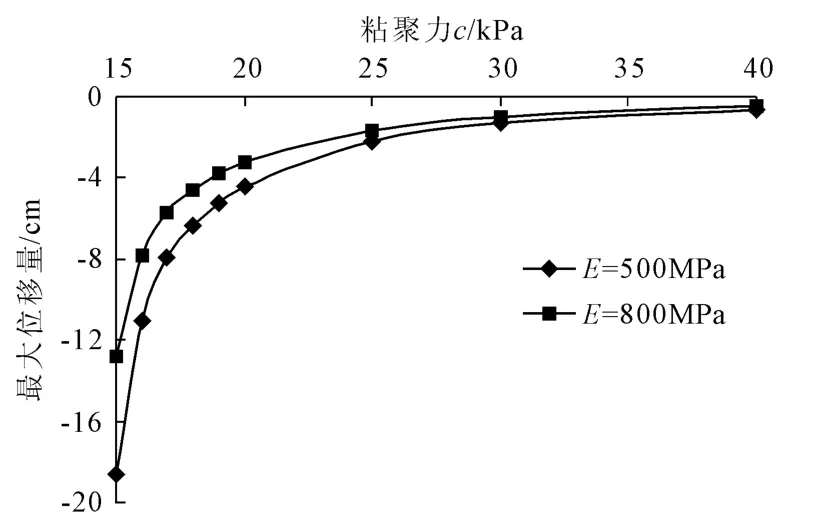
图8 不同粘聚力c下坡面最大下滑位移曲线

图7 所示为不同粘聚力c值下，边坡坡面最大隆起位移关系曲线。可以看出，粘聚力c=15 kPa～20 kPa范围内，坡面最大位移变化均成倍减小，变化幅度显著，随着隧道的不断开挖将会对边坡产生不确定性危害，应予以足够重视，及时采取措施，保证施工安全。当c=20 kPa～25 kPa时，位移变化幅值较为均匀，并未对边坡产生较大扰动。当粘聚力c值继续增大到c=25 kPa～40 kPa范围内，位移变化相当缓慢，对边坡影响不大，不具有实际工程价值。与此同时，不同弹性模量E均符合这一规律。

图8所示为不同粘聚力c值下，边坡坡面最大下滑位移关系曲线。对比图7和图8，可以发现，两种关系曲线形状相似，具有相同的变化趋势。当粘聚力c=15 kPa～20 kPa范围内，隧道的开挖对边坡位移变化的影响显著，实际隧道建设过程中，必须及时监测边坡位移，以免出现崩塌或滑坡等不良地质现象。当粘聚力c=20 kPa～25 kPa范围内，坡顶下滑量变化幅值在合理区间内。随着粘聚力c继续增大，位移变化不明显，此时，粘聚力c将不是影响边坡位移变化的主要因素。

2.2 考虑内摩擦角φ对边坡位移的影响

现取土体弹性模量E=500 MPa，粘聚力 c=25 kPa，分别取 φ =27°，28°，29°，30°，31°，32°，33°(对应的剪胀角降低3°)七个数值，研究不同内摩擦角φ对边坡位移的影响。受篇幅影响，仅列出 φ=27°，29°，30°和 33°四种情况相应的位移等值云图。

图9表示为内摩擦角φ=27°情况下，边坡竖向位移等值云图。坡顶处产生最大下滑位移约为13.3 cm，在坡脚附近有10.0 cm隆起量。在此情况下，隧道附近土体并未产生最大位移，故对其影响并不明显。

图9 内摩擦角φ=27°竖向位移等值云图

图10 所示为内摩擦角φ=29°时边坡竖向位移等值云图。坡面最大下滑位移约为3.5 cm，在坡脚附近约有2.83 cm隆起量。对比图9和图10，可以看出内摩擦角略微增大，其坡面最大位移变化近5倍。说明在这个范围内，内摩擦角的变化对边坡位移影响较大，应及时监测坡面最大位移，以免出现工程事故。

图10 内摩擦角φ=29°下竖向位移等值云图

图11 显示为内摩擦角φ=31°时，边坡竖向位移等值云。坡面最大下滑位移约1.5 cm，坡脚附近最大隆起量为1.3 cm。对比图10和图11，可以看出，内摩擦角继续增大，边坡最大位移仅减小一倍，变化幅值不大，且在许可范围内。

图11 内摩擦角φ=31°下竖向位移等值云图

图12 表明内摩擦角φ=33°情况下，边坡竖向位移等值云图。随着土体内摩擦角继续增大，边坡位移变化十分不明显，此时，内摩擦角将不是影响边坡位移的主要影响因素之一。

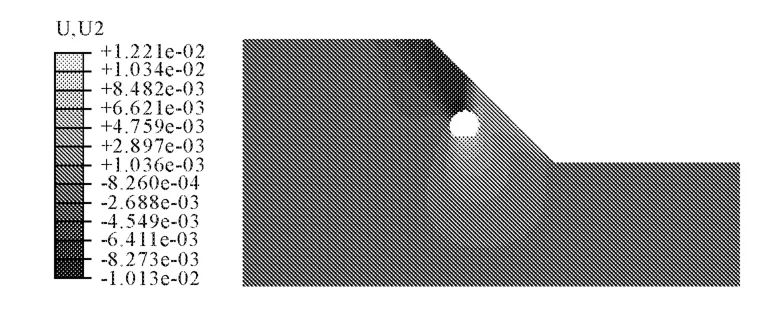
图12 内摩擦角φ=33°下竖向位移等值云图

弹性模量E=800 MPa的情况下，竖向位移等值云图与弹性模量E=500 MPa相近，本文不详细列举。具体各数值下边坡最大位移量见表2，其关系曲线见图13～图14所示。

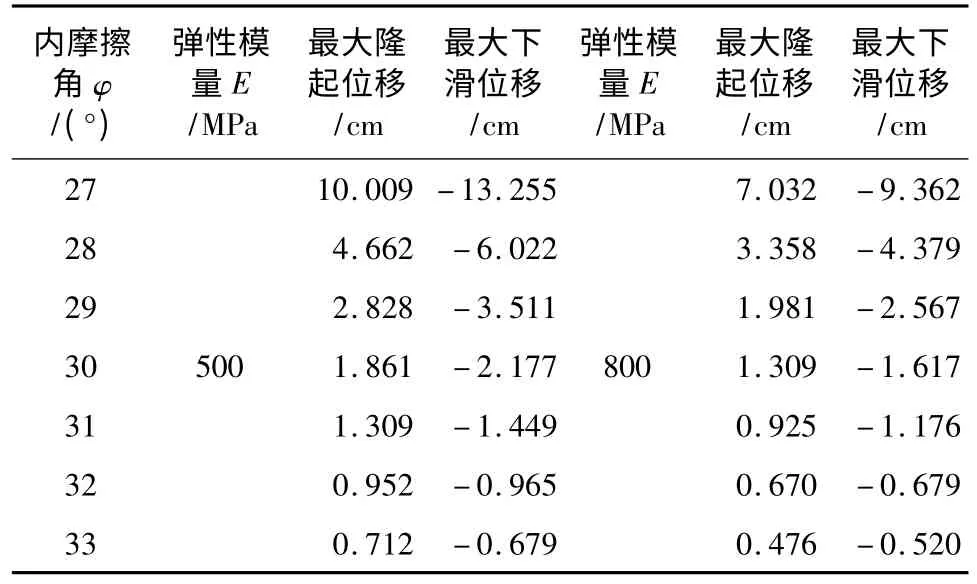
表2 不同内摩擦角φ下坡面最大位移

图13显示出内摩擦角 φ=27°～29°范围内，边坡位移变化较大，基本成倍减小，说明在此范围内，隧道的开挖将影响边坡稳定性，存在一定地安全隐患。当内摩擦角 φ=29°～31°范围内，位移变化量幅值较小，均在设计允许范围内，实际施工对边坡的扰动在可控界限内。当内摩擦角继续增大，φ=31°～33°范围内，位移变化极不明显，曲线趋于平缓，说明内摩擦角的继续增大对边坡位移变化无明显影响。对比图13和图14，可以发现，无论是边坡坡面最大隆起位移还是坡面最大下滑位移，均具有相同的变化趋势。

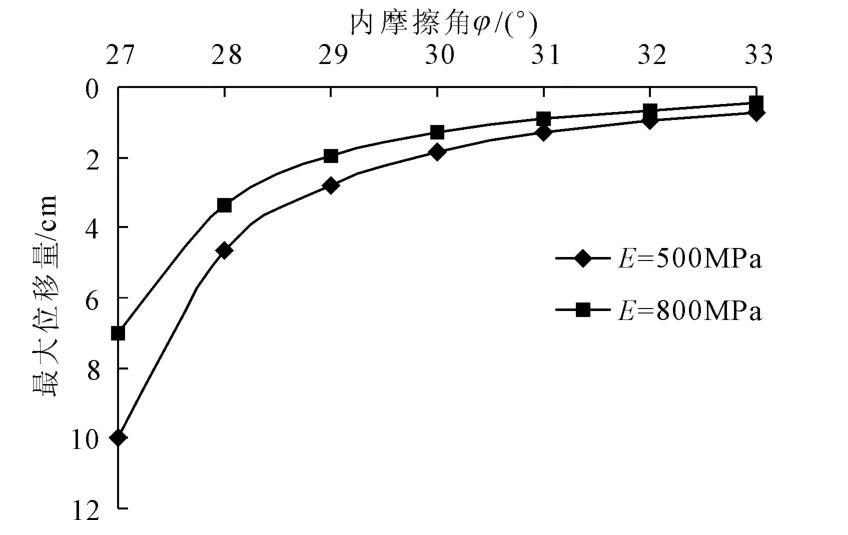
图13 不同内摩擦角φ下坡面最大隆起位移曲线

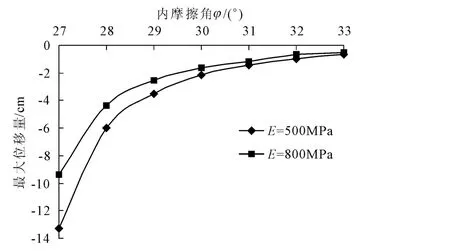
图14 不同内摩擦角φ下坡面最大下滑位移曲线

3 结论

本文研究的主要结论如下:

(1)计算结果表明，土体抗剪强度参数对边坡隧道位移变化有着至关重要的作用。土体强度在偏低范围内取值，随着隧道开挖过程对边坡将产生较大的扰动，有可能出现崩塌或滑坡等不良地质现象。逐渐增大土体强度，边坡位移明显缩小，其变化量在设计与施工要求范围内，可以保证工程的顺利进行。土体强度参数取值继续增大，计算结果变化不显著，对研究此类工程无实际意义。

(2)本文研究结果，主要为此类边坡隧道工程的设计与研究提出实际参考价值。

[1]林鲁生，蒋 刚，白世伟，等.土体抗剪强度参数取值的统计分析方法[J].岩土力学，2003，24(2):277-280.

[2]王 毅.强度参数的取值对边坡稳定分析的影响探讨[J].山西建筑，2009，35(20):90-91.

[3]陈科平，彭文详，林 杭，等.边坡强度参数对于稳定性影响的极限平衡法分析[J].沈阳工业大学学报，2012，34(6):1905-1909.

[4]姜 彤，马 莎，李永新.抗剪强度 c，φ值概率分布对边坡可靠性分析的影响[J].华北水利水电学院学报，2004，25(3):46-49.

[5]李宗坤，杨艳容.土体强度参数统计特性对土石坝边坡可靠性的影响分析[J].中国农村水利水电，2011，(8):146-148，150.

[6]高德军，徐卫亚，郭其达.长江三峡大石板滑坡计算参数反分析[J].河海大学学报，2006，34(1):74-78.

[7]胡必容.土体强度参数与边坡变形破坏研究[J].路基工程，2009，(1):165-166.

[8]王 飞.考虑c，φ相关性边坡稳定性多因素敏感性分析[J].中国水运，2011，11(5):227-229.

[9]汤罗圣，殷坤龙，刘艺梁.基于因子分析和 BP神经网络的滑坡抗剪强度参数取值[J].灾害学，2012，27(4):17-20.

[10]刘子振，言志信，凌松耀，等.非饱和土边坡抗剪强度的力学参数影响及灵敏度分析[J].中南大学学报:自然科学版，2012，43(11):4508-4513.

[11]刁 虎.矿山岩体边坡强度参数选取研究[J].金属矿山，2012，(8):37-39，64.

[12]籍延青，隋来才.山西黄土地区公路边坡强度参数选取方法研究[J].山东理工大学学报:自然科学版，2012，26(6):53-57.

[13]郝建云，赵 欢.基于强度折减法的不同坡角边坡稳定性分析[J].河南城建学院学报，2013，22(2):1-4.

[14]刘慧芬，刘 超.土体抗剪强度参数取值探讨[J].南水北调与水利科技，2013，11(2):83-84.

[15]王金昌，陈页开.ABAQUS在土木工程中的应用[M].杭州:浙江大学出版社，2006.

[16]汪益敏，苏卫国.土的抗剪强度指标对边坡稳定分析的影响[J].华南理工大学学报:自然科学版，2001，29(1):22-25.