高精度低功耗无线传感器网络时间同步算法*

陈孟元，周 娅，郎 朗

(安徽工程大学 安徽省电气传动与控制重点实验室，安徽 芜湖 241000)

高精度低功耗无线传感器网络时间同步算法*

陈孟元，周 娅，郎 朗

(安徽工程大学 安徽省电气传动与控制重点实验室，安徽 芜湖 241000)

通过对无线传感器网络参考广播同步(RBS)算法的研究，针对RBS多跳算法网络开销大和不能实现全网同步的问题，在基于环形网络拓扑的参考广播环形同步(RBRS)算法基础上,提出一种改进的RBRS(IRBRS)算法。该算法引入可变周期同步法：根据贝叶斯最大后验估计原理，估算出最大相位偏差来决定同步周期，从而减少节点同步次数，并且采用最小二乘线性回归法，周期性拟合时钟偏移。运用Matlab环境进行仿真，仿真结果表明：IRBRS算法同步精度显著提高，并且能量消耗显著减少，更有利于延长无线传感器网络的寿命。

无线传感器网络；时间同步；多跳；参考广播同步；误差开销分析

0 引 言

时间同步技术是无线传感器网络(WSNs)的关键技术。由于分布式结构、硬件振荡器以及物理层、介质访问层消息传输延迟的缺陷会导致时间不能同步[1],同时节点的时间同步对无线传感器网络中的能量管理、休眠调度、数据融合、定位追踪以及安全协议等步骤起着关键作用[2]。因此，保持无线传感器网络各节点的时间同步有着现实的意义。在传感器网络节点设计方面，传感器网络的寿命与电池容量呈正比，而且由于空间和其它操作的限制，能量不足会成为传感器网络的实际操作中的现实问题[3]。

不同的算法设计面向不同的应用,传感器网络定时同步协议(timing-sync protocol for sensor networks,TPSN)算法是基于发送接收端之间的时间同步，算法时间精度，计算负荷小，但是鲁棒性差，能耗较参考广播同步(reference broadcast synchronization,RBS)算法大，不适应拓扑结构的变化。本文旨在对中小型网络实现全网的时间同步，针对RBS多跳算法网络开销大和不能实现全网同步的问题，提出一种改进的参考广播环形同步(improved references broadcast ring synchronization，IRBRS)算法。该算法引入可变周期同步法[4]：根据贝叶斯最大后验估计原理[5]，估算出最大相位偏差来决定同步周期[6]，从而减少节点同步次数,并且采用最小二乘线性回归法[7]，周期性拟合时钟偏移，最终实现全网同步。

1 IRBRS算法

针对RBS多跳算法网络开销大和不能实现全网同步的问题，在RBRS算法基础上，IRBRS算法分两步实现网络内所有节点的同步。首先进行可变周期同步法，采用最大后验估计法估计出最大相位偏差，进而调整算法的同步周期，然后采用最小二乘线性拟合对时间偏差和频率偏差进行补偿，最终得到一种多跳高精度低功耗的IRBRS算法。

1.1 可变周期同步

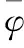
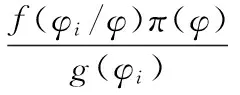
(1)

其中，样本的概率密度相乘得

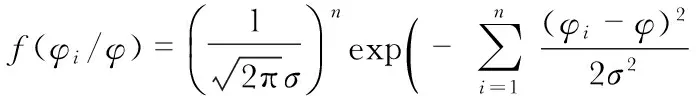
-∞<φi<∞,i=1,2,…,n.

(2)

先验分布为

(3)

边际分布为

(4)

对式(1)取对数

lnπ(φ/φi)=lnf(φi/φ)+lnπ(φ)-lng(φi).

(5)

将式(2)、式(3)、式(4)带入式(5)，对φ求偏导得

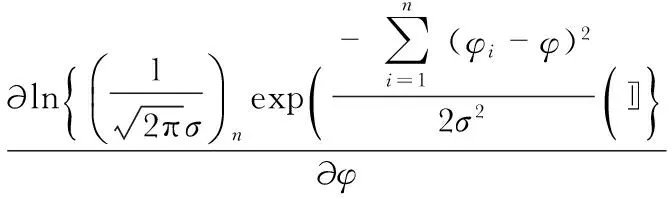
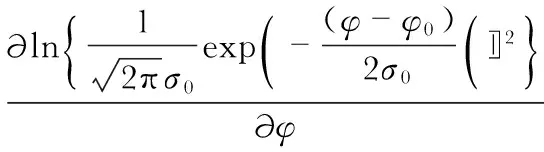
(6)

(7)

则

(8)

式(8)计算最大的相位偏差估计量。根据本次同步的最大相位偏差估计量，可计算出下次同步周期。

设网络要求的同步精度为a，在第n-1同步过程中，最大的传输时延为Tmax，同步周期为Tn-1，并且其同步的最大相位偏差为βmax，T为预计更新周期,则根据

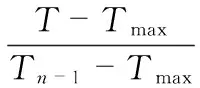
(9)

可求出预计更新周期

(10)

下一次更新周期为

(11)

式中j1，j2为调节因子，j1+j2=1。在预计更新周期T和历史统计周期Tn-1之间权衡计算，生成本次实际更新周期。

一般将最大相位偏差估计量作为一个比较相位偏差，以这个相位偏差值为标准来决定同步的次数。如果本次的最大时钟偏移量较小时，则将下次的同步周期按比例加长;如果本次的最大时钟偏移量较大时，则将下次的同步周期按比例缩短。同步次数减少，能耗降低。

1.2 相位偏差估计

RBS算法采用广播的特性发送消息，消除了来自发送端的发送时延和接收时延的不确定性。节点访问到信道后，空气中的通信时延即传播时延可以忽略。接收时延包括接收数据包、编码以及上报操作系统的时间，随着时钟频率的漂移和初始相位偏差的不同，使得各个节点的本地时钟不同，各个节点间接收时延会有偏差[10]。图1为节点同步时延图。

图1 节点同步时延Fig 1 Simultaneous delay of nodes

因此，需要对时钟频率偏移和初始相位偏差进行估计,可以采用最小二乘线性拟合法。

节点A1和A2之间的本地时钟关系为

tim=aijtjm+bij+ε.

(12)

其中，aij为节点A1相对于节点A2的频率偏差；bij为两个节点本地时钟的初始相位偏差；ε就是两节点接受同一个分组的时间偏差，服从期望为0，方差为σ2的正态分布，具体的推算过程如下：

一般采用最小二乘方法估计模型式(13)中的aij，bij，令

(13)

(14)

(15)

这组方程称为正规方程组，经过整理，可得

(16)

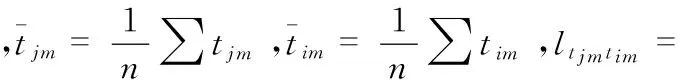
最终求得其结果为

(17)

(18)

a12，b12即完成了两节点时钟漂移的补偿，但是a12，b12解决的是两节点间瞬时的时间漂移。

2 算法仿真分析

为了验证算法的有效性，采用Matlab软件进行仿真。在一个类似于算法的网络拓扑形状摆放24个基于IEEE 802.15.4的无线传感器网络节点进行同步实验。数据传输速率为50 kB/s，数据包大小约为10 kbit。文献[11]已对4跳的线性网络对RBS算法进行了模拟。为了更好地比较RBS算法和IRBRS算法，将继续在4跳的线性网络上模拟IRBRS算法。

IRBRS算法首先采用最大后验估计法估算出最大相位偏差，并通过最大相位偏差估算同步周期值。在不同的周期值内，发送的同步消息量不一样，从而导致了不一样的同步精度值和能量消耗。文献[8]中，Elson J等人通过实验得出相位偏差服从u=0，σ=11.1的正态分布，其中最大相位偏移为53.4 μs。根据最大相位偏差，同步周期内最大的相位偏差总小于或等于总体相位偏差。因此，IRBRS算法同步周期小于或等于RBS算法的最大同步周期。假设RBS算法最大同步周期为600 ms，第一次IRBRS算法的同步周期为300 ms。根据实际的运作情况，图2显示了两种算法的同步周期情况。

图2 同步周期显示Fig 2 Indication of simultaneous cycles

如果同步周期长，同步的次数多，同步误差精准度就越高，因此，下次的同步周期便减小;反之，下次的同步周期就变长。

同步周期的长短和能量消耗值紧密相关。IRBRS算法和RBS算法的传输机制一致，只是传输方式不同。由图2可以看出:RBS算法的同步周期比动态的IRBRS同步周期大。如图3为各算法能耗对比图，IRBRS算法能耗少于RBS的50%，而TPSN 算法在相应节点数量下的能耗最大。

图3 三种算法能耗对比Fig 3 Comparison of energy consumption of three kinds of algorithms

通过最大后验估计法估算出同步周期，在不同的同步周期内，采集时间信息,再将这些时间信息用最小二乘法线性拟合，比较算法的精度，如图4。

图4 三种算法精度对比Fig 4 Comparison of precision of three kinds of algorithms

上述通过仿真得出RBS算法和RBRS算法的同步累积误差相近。IRBRS算法就是在RBRS算法基础上进行优化，4跳结束后，RBS和RBRS的平均误差分别为70.30 μs和81.26 μs，而IRBRS算法的平均误差只有59.87 μs。可以看出：IRBRS算法累积误差明显降低，即同步精度提高。

3 结束语

在经典RBS算法基础上提出RBRS算法虽比较新颖，还没有达到最优化。本文首先通过可变周期的想法，结合最大后验估计法，估算出算法的最大相位偏差，从而改变了算法的同步周期，降低了节点能耗；其次，采用最小二乘法，对周期值内的时间值进行线性拟合，完成对相位偏移和频率偏移的补偿，从而完成了整个同步过程。理论分析和仿真结果表明：IRBRS算法在能耗和同步精度方面均优于RBS和RBRS算法，适用于中小型无线传感器网络，增强了网络时间同步的可靠性。

[1] 孙利民，李建中.无线传感器网络[M].北京：清华大学出版社，2005.

[2] Sivrikaya F,Yener B.Time synchronization in sensor networks: A survey[J].IEEE Network，2004,18(4):45-50.

[3] Elson J,Girod L,Estrin D.Fine-grained network time synchronization using reference broadcasts[C]∥Proceedings of the 5th Symposium on Operating System Design and Implementation,Boston,MA:ACM,2002:147-163.

[4] Ren F Y，Huang H N，Lin C． Wireless sensor networks[J]． Journal of Software，2003，4(7) : 1282-1291．

[5] 王义君，钱志鸿，王桂琴,等.无线传感器网络能量有效时间同步算法研究[J].电子与信息学报，2012，34(9)：2174-2179.

[6] 齐 华，王 恒，刘 军.可变周期的基于贝叶斯估计的 TPSN 改进算法[J].传感技术学报，2013，26(3)：407-410.

[7] 谭 励.无线传感器网络理论与技术应用[M].北京：机械工业出版社，2011.

[8] Elson J,Estrin D.Time synchronization for wireless sensor networks,parallel and distributed processing symposium[C]∥Proceedings of 15th International .Parallel and Distributed Processing Symposium,San Francisco,USA,2001:1965-1970.

[9] Walpole Ronald,Myers Raymond H.周 勇，等译.理工科概率统计[M].北京：机械工业出版社，2009.

[10] Gradowska P L,Cooke R M.Least squares type estimation for Cox regression model and specification error[J].Computational Statistics & Data Analysis,2012,56(7):2288-2302.

[11] Sichitiu M L,Veerarittiphan C.Simple,accurate time synchronization for wireless sensor networks[C]∥Proc of the IEEE Wireless Communications and Networking Conf,2003.

High precision and low power consumption time synchronization algorithm for wireless sensor networks*

CHEN Meng-yuan, ZHOU Ya, LANG Lang

(Anhui Polytechnic University,Anhui Key Laboratory of Electric Drive and Control,Wuhu 241000,China)

Through research of reference broadcast synchronization(RBS) algorithms for wireless sensor networks(WSNs),aiming at problem of large amount of network overhead and the whole network synchronization,an algorithm based on references broadcast ring synchronization(RBRS) is presented,named improved RBRS(IRBRS) algorithm.The algorithm lead into variable cycle synchronization method.According to principle of Bayesian maximum posterior estimation,estimate the maximum phase offset to determine synchronization cycle to reduce the number of node synchronization,it also can fit clock skew periodically by least square linear regression method.Matlab software is used for simulation,results show that IRBRS algorithm synchronous precision is improved obviously and reduce energy consumption significantly to be better for extend life of wireless sensor networks.

wireless sensor networks(WSNs); time synchronization; multi-hop; reference broadcast synchronization(RBS); error overhead analysis

10.13873/J.1000—9787(2014)10—0125—03

2014—07—09

安徽省自然科学基金资助项目(11040606M153);安徽高校省级自然科学研究项目(KJ2013A041)

TP 393；TP 391

A

1000—9787(2014)10—0125—03

陈孟元(1984-)，男，安徽芜湖人，硕士，讲师，主要研究方向为无线传感器网络的优化与时间同步。