En KF中误差协方差优化方法及在资料同化中应用

梁 晓郑小谷戴永久师春香

1）（国家气象信息中心，北京100081）2）（北京师范大学，北京100875）

En KF中误差协方差优化方法及在资料同化中应用

梁 晓1）*郑小谷2）戴永久2）师春香1）

1）（国家气象信息中心，北京100081）2）（北京师范大学，北京100875）

集合卡尔曼滤波（the Ensemble Kalman Filter，简称En KF）中将预报集合的统计协方差作为预报误差协方差，但该估计可能严重偏离真实的预报误差协方差，影响同化精度。基于极大似然估计理论，发展了一种优化预报误差协方差矩阵的实时膨胀方法，即MLE（the Maximum Likelihood Estimation）方法。利用蒙古国基准站Delgertsgot（简称DGS站）观测资料，基于En KF方法和 MLE方法，在通用陆面模式（the Common Land Model，简称Co LM）中同化了地表温度和10 cm土壤温度观测资料，建立了土壤温度同化系统。结果表明：MLE方法对地表温度和各层土壤温度（尤其深层土壤温度）的估计比En KF方法准确。考虑到浅层和深层土壤温度的差别，在实施MLE方法时对浅层和深层土壤温度采用了不同的膨胀因子。对比膨胀因子为单一标量时的结果，多因子膨胀能缓解深层土壤温度的不合理膨胀，改善同化效果。

数据同化；集合卡尔曼滤波；误差协方差膨胀

引 言

集合卡尔曼滤波（the Ensemble Kalman Filter，简称En KF）是目前常用的一种数据同化方法，自Evensen［1］提出和Burgers等［2］发展后，已应用于很多同化研究。理论上，通过将观测资料融入预报模型，数据同化能够实现模型输出和观测资料的最佳融合。但这种“最佳”依赖于预报（背景）误差协方差和观测误差协方差的精度。预报误差协方差和观测误差协方差的估计是否准确，是决定En KF方法同化精度高低的关键［3］。然而，实际应用中很难精确得到这些统计量信息［4］。因此，优化误差协方差的估计，对En KF方法发展十分必要［5-6］。

En KF方法中，通常将预报集合的统计协方差作为真实的预报误差协方差。但研究表明，由于样本量有限，该估计中存在的采样误差会导致预报集合的统计协方差低估真正的预报误差协方差，集合扩散度迅速减小，使得观测对同化的影响越来越小，甚至完全失效，发生滤波发散［7-8］。为此，一种旨在增大集合方差的协方差膨胀技术逐渐发展起来。目前常用的一种方法是给预报集合成员偏离平均值的偏差乘一个略大于1的常数［7］，该方法中的膨胀因子通过反复试验得到，需多次运行同化系统。对于大型复杂的实际模型，这种试验方法的计算代价十分巨大，且膨胀因子在同化时段内不变也不合理。因此，有必要发展无需反复试验并能在同化循环中实时更新膨胀因子的协方差膨胀技术。

Dee［9］及其相关工作［10-11］发展了误差协方差的极大似然估计方法。首先对误差协方差矩阵建立参数化模型，再通过观测减预报得到的残差的极大似然估计来估计模型中的未知参数。但其工作没有提出可靠的误差协方差矩阵参数化模型，因此一直未得到普及。近年来，根据观测减预报得到的残差的统计特征，逐渐提出了一些实时估计膨胀因子的方法［12-14］。然而，这些方法均基于矩估计，而非极大似然估计。

作为极大似然估计方法［9-11］的扩展，Zheng［15］提出了预报误差协方差矩阵的多变量实时膨胀方法，将膨胀因子从常数标量扩展到实时变化的对角矩阵。Liang等［16］基于Zheng［15］的工作，提出了同时膨胀预报和观测误差协方差矩阵的方法，但上述工作只在简单的小模型中进行试验。作为文献［16］工作的延续，本文使用陆面过程模型，将Zheng［15］和Liang等［16］的膨胀方法用于陆面同化。本文的膨胀因子已扩展为对角矩阵，即非标量。

土壤温度是陆面过程中的一个重要变量，可以通过模型模拟或仪器观测得到，但两种手段各有利弊。站点观测反映了观测时间和地点上的真实状态，但由于土壤的空间异质性，它所能代表的空间范围有限，无法满足区域性研究的要求；遥感观测可以得到卫星过境时刻大范围的地表温度信息，但遥感反演过程引入了很大的不确定性，而且只能获得瞬时信息。陆面过程模型可以给出土壤温度在时间和空间上的连续演进，但模型参数、驱动场、初始条件等的不完备都会影响模拟精度。如何有效结合观测和陆面过程模型模拟得到更真实且时空连续的信息，尤为重要，因此陆面数据同化研究越来越多［17-20］。本文将利用通用陆面模式（the Common Land Model，简称Co LM）和两种同化方法发展土壤温度同化方案，改进对土壤温度廓线的估计。为便于表达，未使用和使用本文膨胀方法的En KF方法分别简称为En KF方法和MLE方法。

1 MLE方法

一个非线性时间离散的预报系统和线性观测系统可表示为

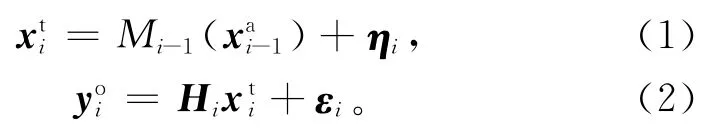
其中，i是积分步数，是真值向量，Mi－1是非线性模型算子，yoi是观测向量，Hi是将状态变量映射到观测空间的观测算子，ηi和εi是背景误差和观测误差向量，假定二者相互独立且时间上不相关，各自服从平均值为0、协方差矩阵分别为背景误差协方差矩阵Pi和观测误差协方差矩阵Ri的高斯分布。同化目标是找到尽可能接近真值的分析状态

En KF方法在很多文献中均有介绍［2，21-22］，不再赘述。En KF方法中通常采用预报集合的采样协方差矩阵Pi（式（3））作为真正的预报误差协方差矩阵

有限的样本量导致该估计中存在较大的采样误差，集合协方差会低估真正的误差协方差，导致滤波发散［23］。最初，抑制滤波发散的方法是给预报集合中每个成员偏离平均值的离差乘略大于1的因子相当于将预报误差协方差矩阵Pi膨胀为原来的λ倍。但该膨胀因子λ随时间不变，且需要多次反复试验来确定［7］。

基于观测减预报得到的残差di的极大似然估计，Zheng［15］和 Liang等［16］提出一种随时间变化的膨胀方法，通过极小化di的似然函数－2Li（λi）（即对di的概率密度函数取－2倍的自然对数）实时估计膨胀因子［λi］：

其中，det表示矩阵的行列式。该方法根据文献［9-11］提出的估计误差协方差方法发展而来，膨胀因子［λi］为对角矩阵，不是标量。

估计得到［λi］后，预报误差协方差矩阵假定为［λi］Pi［λi］，相当于用膨胀后的预报集合重新计算式（3）中定义的预报误差协方差矩阵：

结合预报和观测信息，可计算出i时刻同化更新后的分析集合

式（7）中，ε′i，j为服从平均值为0、协方差矩阵为Ri的正态分布随机扰动。

本文将使用同化结果的均方根误差来评价同化效果。通常来说，均方根误差越小，同化结果越好。

2 试验设计

本文选取国际协同强化观测期计划（Coordinated Energy and Water Cycle Observations Project，简称CEOP）蒙古国基准站Delgertsgot（简称DGS站），使用 En KF和 MLE两种同化方法，在Co LM［24-25］中以12 h 1次的频率同化DGS站地表温度和10 cm土壤温度观测资料，比较两种方法对土壤温度廓线的估计效果。同化系统状态向量包括地表温度、10层土壤温度和10层土壤湿度。本文还分别使用经验算法得到的叶面积指数和MODIS LAI产品，用来分析叶面积指数精度对土壤温度的影响。

2.1 研究区概况及观测数据

蒙古国基准站位于蒙古高原，地表覆盖为均质矮草，观测数据较好［18，26］。其中 DGS站（46.1°N，106.4°E）于2002年10月1日—2003年9月30日进行了地表温度和土壤温度及气象要素的连续观测，本文选取该站开展同化试验。土壤温度的观测深度为3，10，40 cm和100 cm，相应还有土壤湿度观测，30 min 1次。在该站点已开展了一些陆面同化研究［17-18］，本文在选取站点观测资料和研究时段等方面均予以考虑。本研究中，在Co LM中同化了DGS站每日08：00（世界时，下同）和20：00的地表温度和10 cm土壤温度的观测数据，并使用逐时连续的各层土壤温度和土壤湿度观测数据来验证同化结果。

Co LM运行所需的大气驱动数据中，除入射太阳短波辐射和大气长波辐射没有观测资料外，其他变量均来自自动气象站资料。日本气象厅利用其全球数据同化系统为CEOP的基准站提供了始于2002年10月1日的时间分辨率为1 h的大气数据集，Huang等［17］从该数据集获取了蒙古国基准站的太阳短波辐射和大气长波辐射，本研究所需的辐射信息来源于此。

为分析叶面积指数（leaf area index，简称LAI）对土壤温度的影响，本研究还使用MODIS LAI产品代替原模式经验算法计算的叶面积指数，比较使用经验叶面积指数和MODIS LAI产品得到的结果。MODIS LAI产品提供了全球的1 km分辨率的叶面积指数（每8 d 1次），本文从中提取DGS站的2002年10月1日—2003年9月30日的叶面积指数和质量控制说明数据。

2.2 MLE方法的两种情况

本文使用的膨胀因子［λi］是对角矩阵，而不再局限为标量。当［λi］的主对角线上含有不同数值时，即可对不同的状态变量使用不同系数进行不同程度的膨胀；而当［λi］的主对角线上均为相同数值时，膨胀因子［λi］便相当于标量，即对所有的状态变量都使用同一系数进行相同程度的膨胀。

Co LM中地表温度和深层土壤温度的性质差异大，如地表温度随时间变化快且变化幅度大，而深层土壤温度随时间变化平缓。如果对整个土壤温度廓线均采用同一膨胀因子，可能无法兼顾浅层和深层土壤温度膨胀的合理性，最终影响土壤温度廓线的同化效果。因此，本文对浅层和深层土壤温度采用不同的膨胀因子，即膨胀因子矩阵［λi］的主对角线上含有两个待估计的标量膨胀因子λi，1和λi，2。其中［λi］主对角线上的前3个元素值均为λi，1，用于膨胀地表温度和上两层土壤温度（2.8 cm以上）；后8个元素值均为λi，2，用于膨胀下8层土壤温度（2.8 cm以下）；与土壤湿度对应的10个元素值则为1.0，即 不 膨 胀 土 壤 湿 度。由 式 （5）可 知，－2Li（λi）实际上是关于Hi［λi］的函数，即无论膨胀因子矩阵［λi］中包含多少未知参数，通过极小化－2Li（λi）只能估计出Hi［λi］能包含的那些参数。如果被同化的观测信息只有地表温度，则Hi［λi］只包含用于膨胀地表温度和上两层土壤温度的参数λi，1，即 MLE方法通过极小化－2Li（λi）只能估计出λi，1，无法估计出λi，2。为此，本文在同化系统中又引入10 cm土壤温度观测信息，这样Hi［λi］中就同时包含了λi，1和λi，2，从而保证 MLE方法可以同时估计得到这两个参数。

为探讨对浅层和深层土壤温度进行不同程度膨胀的必要性，本文将比较浅层和深层土壤温度使用同一系数和不同系数进行膨胀时的结果。为便于表达，浅层和深层土壤温度使用同一膨胀系数和不同膨胀系数的MLE方法分别简称为MLE1方法和MLE2方法。

3 同化结果

3.1 确定观测算子和观测误差

本研究同化的观测变量为地表温度和10 cm土壤温度，状态变量为地表温度、10层土壤温度和10层土壤湿度。

本研究同化的地表温度观测是站点观测数据，观测变量与模型中的地表温度变量一致，故地表的观测算子为1。本研究还同化了站点观测的10 cm土壤温度，而这一深度无法与Co LM中定义的任一层土壤节点的深度直接对应。因此，利用相邻两层模拟深度上的土壤温度经线性内插得到10 cm土壤温度，该插值算法即为10 cm深度观测算子：

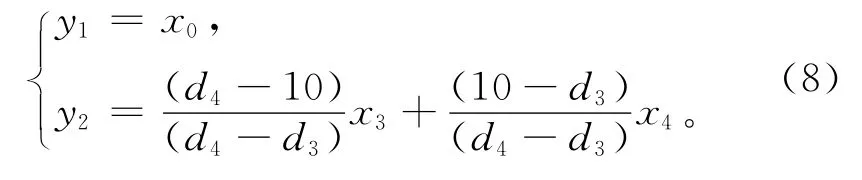
其中，y1和y2分别为地表和10 cm土壤温度的模拟值，d3和d4分别为Co LM中第3层和第4层土壤节点的深度（6.2 cm和11.9 cm），x0为Co LM 的地表温度模拟值，x3和x4分别为Co LM中第3层和第4层的土壤温度模拟值。该观测算子将Co LM输出的模型状态变量与观测变量联系起来。

在DGS站，地表温度使用4000.4G红外温度传感器观测，土壤温度使用温度计观测。查阅相关仪器手册，最终确定地表温度和10 cm土壤温度的观测误差分别为1.0 K和0.5 K。

3.2 同化结果

使用DGS站2002年10月1日—2003年9月30日的观测数据进行试验。Co LM从2002年10月1日积分到2003年5月29日，作为spin-up使模型达到平衡，2003年5月30日同化开始，积分步长为1 h。基于En KF方法和MLE方法，Co LM每12 h同化1次地表温度和10 cm土壤温度观测数据（08：00和20：00），集合样本量为100。选用研究时段为2003年9月1—30日不同深度的土壤温度来验证同化效果。

浅层土壤温度的时间变化较快且变幅较大，很难区分其在30 d内的观测场、模拟场和同化场。因此，对地表温度和3 cm土壤温度在30 d内的结果进行平均，得到其日变化（图1）。En KF方法和MLE方法对地表温度（图1a）和3 cm土壤温度（图1b）的估计都比模拟值准确，尤其在09：00—23：00时段。与模拟相比，En KF方法在01：00—07：00有所低估，MLE方法在此时段内的结果则可以与模拟场相当甚至更优。

图1 2003年9月1—30日地表温度（a）和3 cm土壤温度（b）观测场、模拟场和同化场平均日变化Fig.1 The diurnal variation of observed，simulated and assimilated soil temperature at 0 cm（a）and 3 cm（b）averaged from 1 Sep to 30 Sep in 2003

图2为2003年9月1—30日10 cm和40 cm土壤温度的观测场、模拟场和同化场。在10 cm深度（图2a），En KF方法和MLE方法均比模拟更准确地估计出了土壤温度日变化的趋势和幅度，但MLE方法相比En KF方法的优势不大。在40 cm深度（图2b），与观测场相比，模拟场明显低估，而两种同化方法均有效改善了这种低估，且MLE方法同化得到的土壤温度比En KF方法更接近观测。100 cm的结果与40 cm相似（图略）。

图2 2003年9月1—30日10 cm（a）和40 cm（b）土壤温度观测场、模拟场和同化场变化Fig.2 The observed，simulated and assimilated soil temperature at 10 cm（a）and 40 cm（b）from 1 Sep to 30 Sep in 2003

表1为各层土壤温度模拟场和同化场在2003年9月1—30日平均的均方根误差。En KF方法和MLE方法同化得到的均方根误差均低于模拟结果的均方根误差，而且膨胀因子为对角矩阵的MLE2方法比En KF方法更好。表1还表明，同化对土壤温度估计效果的改善在10 cm，40 cm和100 cm深度比0 cm和3 cm深度明显。浅层的土壤温度变化较快且变幅较大，因此，虽然同化时刻的同化结果会接近观测值，但同化时刻后，在持续较长的预报时间内，变化很快的浅层土壤温度会以较快的速度向模型模拟结果靠拢，导致上一步同化对浅层土壤温度的改善在下一步同化到来时影响不大。这样，同化时刻对浅层土壤温度造成的影响就很难在整个预报过程中得到有效保持和传递。为进一步分析该问题，本文单独针对2003年9月1—30日每日08：00和20：00的同化时刻，统计了膨胀因子为对角矩阵的MLE2方法同化得到的地表温度、3 cm和10 cm土壤温度在同化更新前的背景场均方根误差和同化更新后的分析场均方根误差。总的来说，时间平均的地表温度、3 cm和10 cm土壤温度同化场均方根误差（分别为0.402，1.920 K和0.157 K）均显著低于背景场均方根误差（分别为3.028，3.509 K和1.110 K），这表明同化更新后的同化场比背景场更加接近观测。这与前面的分析一致：在每日两次的同化时刻，同化的确对浅层土壤温度产生了较大影响，但这种影响很难在整个预报过程中得到有效保持。

考虑到浅层和深层土壤温度的性质不同，本文在实施MLE方法时，对浅层和深层土壤温度采用了不同的膨胀因子。从2003年9月1—30日平均结果看，MLE1方法（浅层和深层土壤温度使用同一系数进行膨胀）中地表温度和10层土壤温度的膨胀因子值均为2.2，而MLE2方法（浅层和深层土壤温度使用不同系数进行膨胀）中地表温度和上两层（0.7～2.8 cm）土壤温度的膨胀因子值为3.2，下8层（6.2～286.5 cm）土壤温度的膨胀因子值为1.3。可见，MLE1方法和MLE2方法都通过膨胀因子而对预报误差协方差矩阵的离散度发挥了作用。但MLE1方法没有对浅层和深层土壤温度区别膨胀，导致深层土壤温度膨胀过度；而MLE2方法对浅层和深层土壤温度采用了不同的膨胀因子，使得深层土壤温度的膨胀相对合理。表1中分别列出了MLE1和MLE2方法得到的土壤温度的均方根误差。可以看到，MLE1方法对各层土壤温度的估计均没有MLE2方法准确，尤其对于深层土壤温度（40 cm和100 cm），MLE1方法同化得到的均方根误差比MLE2方法高50%以上，甚至比En KF方法同化得到的均方根误差还高。图3为En KF方法、MLE2方法和MLE1方法同化得到的40 cm和100 cm土壤温度。由图3可见，由于MLE1方法对整个土壤温度廓线都采用同一因子进行膨胀，将适用于变化很快的浅层土壤温度的膨胀因子，也用于膨胀变化较慢的深层土壤温度，造成深层土壤温度被不合理膨胀，进而影响了深层的同化效果。

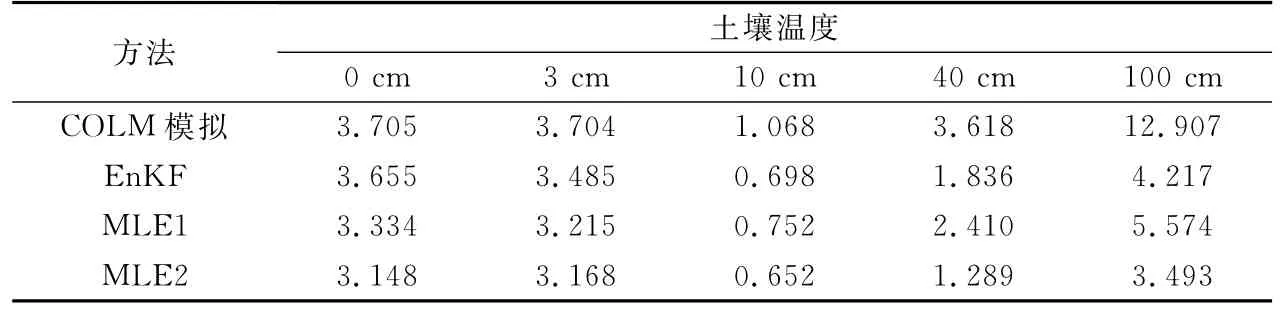
表1 2003年9月1—30日土壤温度模拟场和同化场平均的均方根误差（单位：K）Table 1 Root mean square error of the simulated and assimilated soil temperature from 1 Sep to 30 Sep in 2003（unit：K）

图3 MLE1方法和MLE2方法分别同化得到2003年9月1—30日40 cm（a）和100 cm（b）土壤温度Fig.3 Soil temperature at 40 cm（a）and 100 cm（b）assimilated by MLE1 and MLE2 from 1 Sep to 30 Sep in 2003

图4为2003年9月1—30日3 cm近地表土壤湿度的观测场、模拟场和同化场。与观测相比，Co LM的模拟普遍高估了土壤湿度，而En KF方法和MLE方法均对此有所缓解，且MLE方法的改善更明显。这表明，虽然同化过程中没有引入土壤湿度的观测信息，同化过程仍可以通过误差协方差矩阵和模式传输而影响土壤湿度。

图4 2003年9月1—30日3 cm土壤湿度观测场、模拟场和同化场Fig.4 The observed，simulated and assimilated soil moisture at 3 cm from 1 Sep to 30 Sep in 2003

4 结论和讨论

本文基于极大似然估计理论，发展了一种优化预报误差协方差的实时膨胀方法——MLE方法。当然，除了协方差膨胀方法外，国内外在预报误差协方差的分析和优化方法上还有很多其他研究［27-30］，这些超出了本文目前的研究范围，有待于下一步的跟踪和关注。本研究表明：

1）总的来说，MLE方法对地表温度和各层土壤温度的估计都比En KF方法准确，对深层土壤温度（40 cm和100 cm）尤其如此。

2）考虑到浅层和深层土壤温度的差别，本文对浅层和深层土壤温度采用不同的膨胀因子，即MLE2方法。与膨胀因子为单一标量值时的MLE1方法比较表明，由于对整个土壤温度廓线采用相同的膨胀因子，MLE1方法对各层（尤其深层）土壤温度的估计没有MLE2方法准确。这表明，多因子膨胀可以缓解深层土壤温度的不合理膨胀问题。

3）为分析叶面积指数对土壤温度的影响，本文在Co LM中引入MODIS LAI产品代替经验算法计算的叶面积指数。结果表明，与使用经验叶面积指数相比，使用MODIS LAI可以改善Co LM对地表温度和3 cm土壤温度的模拟，对地表温度和各层土壤温度的同化也更加准确。

本文在估算模型误差协方差矩阵时使用对角矩阵（协方差项为0），没有考虑不同土壤层变量之间的相关。Jin等［31］研究表明，当合理给定模型误差协方差矩阵中的协方差项时，同化系统能将表层优化后的信息快速传递给深层，从而快速显著改善整个土壤廓线状态变量的估计。但其工作是单独优化土壤温度或湿度，未涉及土壤温度与湿度之间的误差协相关。在同步优化土壤温度和土壤湿度时，如何确定土壤温度和湿度之间的协相关，值得研究。

本文膨胀因子随时间变化，但在空间上不变，这实际上不合理，尤其是观测资料在空间上分布不均匀时。适用于观测资料浓密区的膨胀因子，若持续用于所有地区，可能导致观测资料稀疏区过度膨胀。为对浅层和深层土壤温度进行不同程度的膨胀，本文引入了10 cm土壤温度的观测信息。如果随时空变化的膨胀方法得以实现，则仅同化地表温度就能针对不同深度的土壤温度估计出不同的膨胀因子。Anderson［32］提出的方法中膨胀因子时空上均可变化，但其工作只考虑了观测误差空间独立的情况，不利于遥感资料在同化中的应用。因此，有必要发展适用于空间相关观测系统的、时空变化的膨胀方法。

［1］ Evensen G.Sequential data assimilation with a nonlinear quasi-geostrophic model using Monte-Carlo methods to forecast error statistics.J Geophys Res，1994，99（C5）：10143-10162.

［2］ Burgers G，Leeuwen P J V，Evensen G.Analysis scheme in the Ensemble Kalman Filter.Mon Wea Rev，1998，126：1719-1724.

［3］ Evensen G.The ensemble Kalman filter：Theoretical formulation and practical implementation.Ocean Dynam，2003，53（4）：343-367.

［4］ Senegas J，Wackernagel H H，Rosenthal W，et al.Error covariance modeling in sequential data assimilation.Stoch Env Res Risk A，2001，15：65-86.

［5］ Daley R.Atmospheric Data Analysis.Cambridge：Cambridge University Press，1991.

［6］ Kalnay E.Atmospheric Modeling，Data Assimilation，and Predictability.Cambridge：Cambridge University Press，2002.

［7］ Anderson J L，Anderson S L.A Monte Carlo implementation of the non-linear filtering problem to produce ensemble assimilations and forecasts.Mon Wea Rev，1999，127：2741-2758.

［8］ Constantinescu E M，Sandu A，Chai T，et al.Ensemble-based chemical data assimilation.I：General approach.Q J R Meteorol Soc，2007，133：1229-1243.

［9］ Dee D P.On-line estimation of error covariance parameters for atmospheric data assimilation.Mon Wea Rev，1995，123（4）：1128-1145.

［10］ Dee D P，da Silva A M.Maximum-likelihood estimation of forecast and observation error covariance parameters.PartⅠ：Methodology.Mon Wea Rev，1999，127：1822-1834.

［11］ Dee D P，Gaspari G，Redder C，et al.Maximum-likelihood estimation of forecast and observation error covariance parameters.PartⅡ：Applications.Mon Wea Rev，1999，127：1835-1849.

［12］ Wang X，Bishop C H.A comparison of breeding and ensemble transform Kalman filter ensemble forecast schemes.J Atmos Sci，2003，60：1140-1158.

［13］ Li H，Kalnay E，Miyoshi T.Simultaneous estimation of covariance inflation and observation errors within an ensemble Kalman filter.Q J R Meteorol Soc，2009，135（639）：523-533.

［14］ Miyoshi T.The gaussian approach to adaptive covariance inflation and its implementation with the Local Ensemble Transform Kalman Filter.Mon Wea Rev，2011，139：1519-1535.

［15］ Zheng X G.An adaptive estimation of forecast error covariance parameters for Kalman filtering data assimilation.Adv Atmos Sci，2009，26：154-160.

［16］ Liang X，Zheng X G，Zhang S P，et al.Maximum likelihood es-timation of inflation factors on error covariance matrices for ensemble Kalman filter assimilation.Q J R Meteorol Soc，2011，138：263-273，doi：10.1002／qj.912.

［17］ Huang C L，Li X，Lu L.Retrieving soil temperature profile by assimilating MODIS LST products with ensemble Kalman filter.Rem Sens Environ，2008，112：1320-1336.

［18］ Yang K，Koike T，Kaihotsu I，et al.Validation of a dual-pass microwave land data assimilation system for estimating surface soil moisture in semiarid regions.J Hydrometeorology，2009，10（3）：780-793.

［19］ 杨晓峰，陆其峰，杨忠东.基于AMSR-E土壤湿度产品的LIS同化试验.应用气象学报，2013，24（4）：435-445.

［20］ 吴统文，宋连春，刘向文，等.国家气候中心短期气候预测模式系统业务化进展.应用气象学报，2013，24（5）：533-543.

［21］ 王莉，黄嘉佑.Kalman滤波的试验应用研究.应用气象学报，1999，10（3）：276-282.

［22］ 赵晓琳，朱国富，李泽椿.基于TIGGE资料识别适应性观测敏感区的应用研究.应用气象学报，2010，21（4）：405-415.

［23］ Whitaker J S，Hamill T H.Ensemble data assimilation without perturbed observations.Mon Wea Rev，2002，130：1913-1924.

［24］ Dai Y J，Zeng X B，Dickinson R E，et al.The common land model.Bull Amer Meteor Soc，2003，84：1013-1023.

［25］ 孟春雷，张朝林.路面气象数值预报模型及性能检验.应用气象学报，2012，23（4）：451-458.

［26］ Koike T.Coordinated Enhanced Observing Period （CEOP）-An initial step for integrated global water cycle observation.World Meteorological Organization Bulletin，2004，53（2）：115-121.

［27］ 龚建东，赵刚.全球资料同化中误差协方差三维结构的准确估计与应用：背景误差协方差调整与数值试验分析.气象学报，2006，64（6）：669-682.

［28］ 曹小群，黄思训，张卫民，等.区域三维变分同化中背景误差协方差的模拟.气象科学，2008，28（1）：8-14.

［29］ 马旭林，庄照荣，薛纪善，等.GRAPES非静力数值预报模式的三维变分资料同化系统的发展.气象学报，2009，67（1）：50-60.

［30］ 王曼，李华宏，段旭，等.WRF模式三维变分中背景误差协方差估计.应用气象学报，2011，22（4）：482-492.

［31］ Jin R，Li X.Improving the estimation of hydrothermal state variables in the active layer of frozen ground by assimilating in situ observations and SSM／I data.Sci China Ser D：Earth Sci，2009，39（9）：1220-1231.

［32］ Anderson J L.Spatially and temporally varying adaptive covariance inflation for ensemble filters.Tellus，2009，61：72-83.

A Method of Improving Error Covariances in En KF and Its Application to Data Assimilation

Liang Xiao1）Zheng Xiaogu2）Dai Yongjiu2）Shi Chunxiang1）

1）（National Meteorological Information Center，Beijing100081）
2）（Beijing Normal University，Beijing100875）

In the ensemble Kalman filter（En KF），the forecast error covariance matrix is estimated as the sampling covariance matrix of the forecast ensemble.However，previous studies suggest that the sampling error resulting from finite-size ensembles may make such estimations far from the true forecast error covariance，and finally degrade the performance of En KF.A common way to address this problem is covariance inflation with a time-constant inflation factor.A time-dependent infiation approach on forecast error covariance matrix（i.e.，MLE method）is developed based on the maximum likelihood estimation theory，so as to improve estimates of forecast error covariances.At Delgertsgot（DGS）Station in the Mongolian Plateau reference site，point observations of ground temperature and soil temperature at the depth of 10 cm are assimilated into the Common Land Model（Co LM）with a frequency of every 12 hours，using two assimilation algorithms（En KF method and MLE method），in order to test the effectivity of MLE in practical assimilation.In this way，a soil temperature assimilation system is constructed on the point scale.

Results indicate that MLE method performs better than En KF method for ground temperature and soil temperatures at most depths（especially for soil temperatures at deeper depths）.Moreover，considering differences between soil temperatures at shallower depths and those at deeper depths，different inflation factors are adopted to them when implementing MLE method.Compared to results of MLE using a single scalar inflation factor，it shows that multiple-factor inflation is able to alleviate the unreasonable inflation of soil temperatures at deeper depths and therefore get better assimilation results.In addition，the leaf area index（LAI）in the Co LM is updated dynamically by MODIS LAI products，and results derived using MODIS LAI are compared to those derived using LAI computed by experiential formula，so as to study the effect of the LAI accuracy on simulated and assimilated soil temperatures.It shows that using MODIS LAI can get better simulation of soil temperature at depths of 0 cm and 3 cm，as well as more accurate assimilation of soil temperature at most depths.

The inflation factor is set to be variable in time，but constant in space.However，variables such as soil temperature and soil moisture behave quite differently at shallow surfaces and deep depths，and observations may be unevenly distributed in space in regional assimilation researches.Therefore，it is necessary to adopt different inflation factors to different variables or to the same variable at different locations.In the future，it is necessary to develop a time-and-space dependent inflation method and test its capability in real applications.

data assimilation；En KF；error covariance inflation

梁晓，郑小谷，戴永久，等.En KF中误差协方差优化方法及在资料同化中应用.应用气象学报，2014，25（4）：397-405.

2014-01-06收到，2014-05-05收到再改稿。

公益性行业（气象）科研专项（GYHY201206013，GYHY201306045），国家国际科技合作专项（2011DFG23150）

*email：liangx＠cma.gov.cn