交错网格任意阶导数有限差分格式及差分系数推导

杨庆节，刘 财，耿美霞，冯 晅，郭智奇，刘 洋

吉林大学地球探测科学与技术学院,长春 130026

交错网格任意阶导数有限差分格式及差分系数推导

杨庆节，刘 财，耿美霞，冯 晅，郭智奇，刘 洋

吉林大学地球探测科学与技术学院,长春 130026

交错网格有限差分算法以其高效、精确、实用等优点在地震波数值模拟中得到广泛应用。目前交错网格有限差分的精度已达到时间4阶、空间2N阶；然而在求空间三次导数时，差分格式实际上并未达到所谓的2N阶精度，而是采用了低阶的差分格式及差分系数,这样有利于提高大尺度空间正演时的计算效率；但从计算精度的角度考虑，有必要推导出准确的满足2N阶精度的交错网格有限差分格式及差分系数，以得到更高精度的正演结果。笔者利用Taylor公式展开首次推导出了可导函数任意次导数的任意偶数阶精度的差分近似式及相应的差分系数，从而完善了常规高精度交错网格有限差分算法。采用新推导的交错网格有限差分格式得到的正演波形与解析解进行了对比，证明了新推导的差分格式的正确性，并与常规差分格式的正演波形进行了比较，结果显示,新推导出的交错网格有限差分格式模拟结果稳定性好，精度更高。

交错网格；差分格式；差分系数；高精度

0 引言

随着我国石油天然气勘探开发工作的不断发展，研究人员面临的勘探对象和开发条件越来越复杂，越来越困难。寻找复杂构造油气藏、岩性油气藏和裂缝油气藏等“剩余油”的任务艰巨[1-2]。为了解决这些复杂油气藏的勘探、开发问题，需要对地下复杂介质的地震响应进行高精度数值模拟研究。对地震弹性波方程进行数值模拟的方法主要包括有限差分法、有限元法和伪谱法[3]，而有限差分法由于计算速度快、精度高等特点使用最为广泛[4-5]。

自从Alterman和Karal首次将有限差分法应用到各向同性介质弹性波的模拟中后，由于其自身的优点，很快被用于各种地震勘探学的数值问题上，且在应用中不断发展[6],先后出现了变网格有限差分[7-8]、非连续网格有限差分[9]、不规则网格有限差分[10]、交错网格有限差分[11-13]、旋转交错网格有限差分[14-15]、可变时间步长有限差分[16]、自适应可变空间步长网格有限差分以及隐式有限差分[17-18]。其中，交错网格由Madariage[11]最早提出，Virieux[12]首先将其使用到一阶速度-应力方程中。

为了避免对弹性常数进行空间微分，在弹性波正演模拟时，采用一阶速度-应力弹性波方程。这样可以在不同的时间层上使用不同的网格，分别进行应力和速度的计算和传播。Virieux发展的交错网格精度为O(Δt2+Δx2)(时间2阶、空间2阶)，与常规网格相比，在没有增加计算量和存储空间的情况下，局部精度提高了4倍，收敛速度也有所提高。Levander[19]又将交错网格有限差分的精度提高到O(Δt2+Δx4)。随后董良国等[20-21]发展了更高精度的交错网格有限方法，精度达到了O(Δt4+Δx2N)。为了使用较少的时间层，不增加计算存储空间，董良国等[20-21]将速度(应力)对时间的奇数次高阶导数转化为应力(速度)对空间的导数，把交错网格和高阶差分法成功地结合在一起。然而在高阶交错网格有限差分算法中，当变量对空间求三次导数时，采用的是低阶的差分格式和差分系数[22-25]，没有充分考虑“空间2N阶精度”这一事实，这样做虽然有助于提高有限差分的计算效率，但要想获得更高精度的正演结果就有必要推导出准确的时间4阶、空间2N阶精度的交错网格有限差分格式及相应的差分系数。

差分系数是决定交错网格有限差分算法精度的关键，Taylor公式展开和最优化方法是求取差分系数的主要方式[1,17,26,28]。本文以Taylor公式展开为基础，推导了可导函数任意次导数的任意偶数阶精度的差分近似式以及差分系数，完善O(Δt4+Δx2N)一阶速度-应力方程组差分格式。

1 常规交错网格差分格式

在二维各向同性介质xoz平面内，假定体力为0，一阶速度-应力弹性波方程为

(1-1)

(1-2)

(1-3)

(1-4)

(1-5)

其中：vx,vz为速度分量；τxx,τzz,τxz为应力分量；ρ为密度；c11，c13，c33，c44为介质的弹性常数。

1.1 时间2M阶差分近似

(2)

式中，Δt为时间步长。令M=2，式(2)就是常规的时间4阶精度差分近似。

为了减少计算内存，利用速度和应力的耦合关系，得到方程组式(1)的时间4阶精度差分近似，以式(1-1)为例

(3)

1.2 空间2N阶差分近似以及差分系数

在常规交错网格算法中，速度(应力)分量的空间一次导数是由相错半网格点的应力(速度)分量计算的。设函数f(x)具有2N-1阶导数，令x=x0±[(2n-1)/2]Δx，则由f(x)在x处的2N-1阶Taylor展开可以得到式(3)中空间一次导数的差分近似式

(4)

(5)

实心球表示函数值在半网格点上，空心球表示函数值在整网格点上。图1 差分形式示意图Fig.1 Schematic differential form

1.3 常规时间4阶空间2N阶差分格式

取x=iΔx，z=jΔz，t=kΔt，i、j和k分别表示空间和时间网格点，U、V分别代表速度分量vx、vz的离散值，R、T、H分别代表应力τxx、τzz、τxz的离散值。则方程(3)的精度为O(Δt4+Δx2N)的常规差分格式如下(Δx=Δz，下同)

(6)

可以明显地看出，式(6)中P11、P12、P13、P14及P15的差分格式不是空间2N阶精度的，而是用低阶差分格式代替。

2 任意阶导数有限差分近似式及差分系数推导

为了得到交错网格有限差分的时间4阶、空间2N阶精度准确的差分格式及差分系数，首先需要推导出函数对空间二次、三次导数的差分格式及差分系数，然后将其代入到一阶速度-应力波动方程组中，从而推导出该方程组精度为时间4阶、空间2N阶的准确差分格式。

2.1 函数任意次导数差分近似的差分系数

函数对空间任意次(奇数、偶数次)导数的差分近似式与空间一次导数的差分近似式形式相同，只是差分系数不同；所以推导函数任意次导数的准确的差分近似式的关键就是推导差分系数。交错网格有限差分算法中，求离散化函数f在x=x0的导数时，假设x0为整网格点，差分形式有2种情况，一种是参与计算的函数值在半网格点上，另一种是参与计算的函数值在整网格点上，如图1所示。

首先推导离散化函数值在半网格点上时，差分近似式的差分系数。令函数f(x)在x=x0±[(2n-1)/2]Δx两处的Taylor展开式相减，得

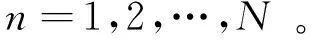
(7)

写成矩阵的形式为

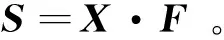
(8)

其中

令

即X=B·D，所以F=D-1·B-1·S。若设F=C·S，则有

(9)

式中，C就是差分系数矩阵。由于D是初等矩阵，所以

则式(9)可写为

(10)

式中，j=1,2,…,N。

为方便起见，只观察式(10)中的第一个式子，两边取转置有

整理有

即

(11)

通过求解式(11)可以得到变量一次导数的差分近似式的准确差分系数，其精度达到2N阶。同理式(10)中其他的N-1个式子都可以得到类似式(11)的方程，即

(12)

(13)

再令函数f(x)在x=x0±[(2n-1)/2]Δx处的Taylor展开式相加，得

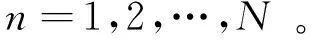
(14)

使用推导任意奇数次导数差分近似式和差分系数相同的方法，从式(14)可得任意偶数次导数差分近似式为

(15)

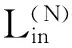
(16)

下面推导离散化函数值在整网格点上时，差分近似式的差分系数。令f(x)在x=x0±nΔx处进行Taylor展开，与函数值在半网格点上时的推导过程类似，该情况下的差分近似式及差分系数求解方程为

(17)

(18)

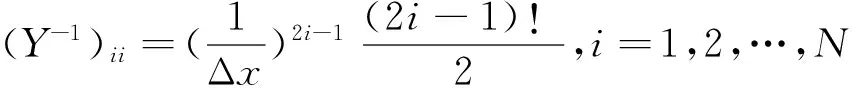
(19)

(20)

式(17)和式(19)分别表示离散化函数值在整网格点上时的任意奇数次和任意偶数次导数的差分近似式，其差分精度与半网格点上的一致。同时给出了差分系数的求解矩阵方程即(18)和(20)式。这样函数f任意次导数的准确的差分近似式以及相应的差分系数全部推导完毕。

2.2 准确的时间4阶、空间2N阶差分格式

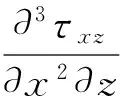
图2 τxz对x一次偏导、对z二次偏导的差分示意图Fig.2 τxz on x of a partial derivative and on z of secondary partial derivative

在确定了差分系数之后，将对应的变量对空间二次、三次导数差分近似式代入到一阶速度-应力方程式(1-1)中，经过整理，得到其精度为O(Δt4+Δx2N)的准确差分格式：

(21)

方程(21)是一阶速度-应力方程式(1-1)的精度为时间4阶、空间2N阶的通式，达到真正的空间2N阶精度。其中的差分系数如表1所示。

3 稳定性以及边界条件

通过傅里叶分析方法，得到二维各向同性介质xoz面内O(Δt4+Δx2N)精度的稳定性条件[21]：

式中，vP为纵波速度。

在模型试算时，笔者采用Collino[27]提出的完全匹配层(PML)吸收边界条件对模型边界进行处理，该完全匹配层(PML)能够很好地吸收进入边界的地震弹性波，消除了边界反射对正演结果的影响。

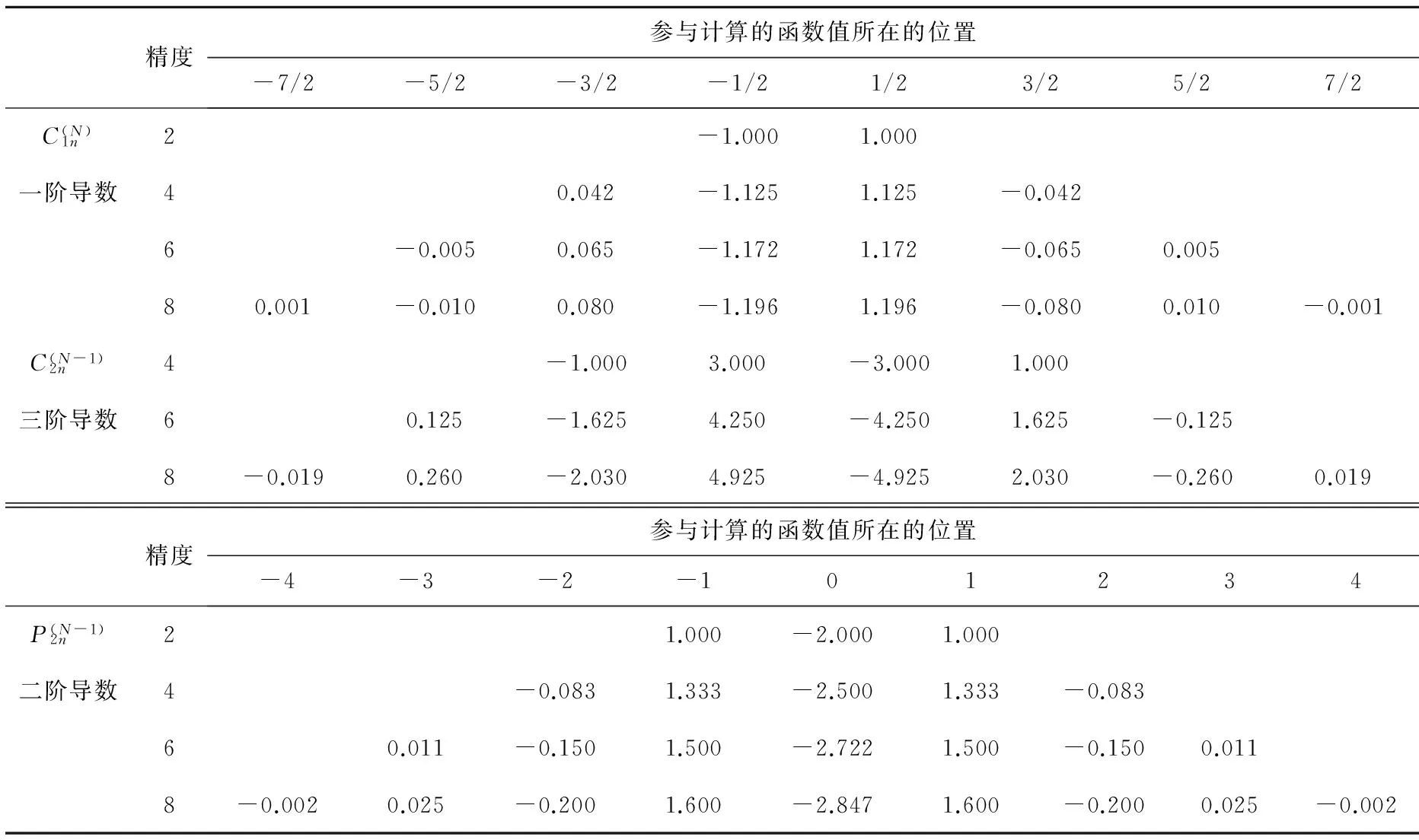
表1 精度为O(Δt4+Δx2N)的差分系数

表2 常用差分精度的稳定性条件

Table 2 Stability conditions of common difference accuracy

差分精度WO(Δt4+Δx6)≤0.9068O(Δt4+Δx8)≤0.8753O(Δt4+Δx10)≤0.8553O(Δt4+Δx12)≤0.8410

4 模型试算

4.1 正确性验证与精度对比

正演时采用各向同性均匀介质模型如图3所示。物性参数为纵波速度vP=3 000 m/s，横波速度vS=2 000 m/s，介质密度ρ=2 000 kg/m3。模型网格大小为200×200，震源坐标为(1 000 m，200 m)，空间步长为10 m，时间采样间隔为0.001 s，用主频为25 Hz的Richer子波激发。模型边界采用PML吸收边界。2个接收器分别位于A(800 m，600 m)和B(1 000 m，600 m)。

五角星表示震源位置，A、B点表示接收器位置。图3 各向同性均匀介质模型Fig.3 Isotropic homogeneous model with its properties

图4a和图4b分别对应A点和B点的地震记录，其中新推导出的交错网格有限差分计算时采用时间4阶、空间8阶精度。从图4中可以看出,无论在波初至还是在震相波形上都基本一致。从而证明了本文推导出的差分格式及差分系数是正确的。

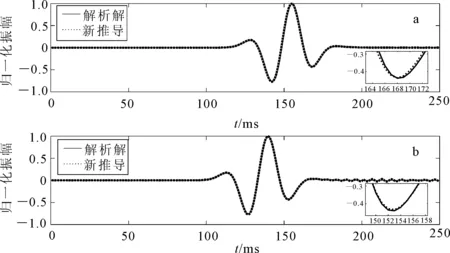
a.A点；b.B点。图4 新推导交错网格差分格式的正演波形与解析解波形比较Fig.4 Comparisons between improved staggered-grid finite difference format solution waveform and analytic solutions waveform

为了进一步研究新推导的交错网格有限差分的计算精度，对其与常规交错网格有限差分正演波形分别和解析解波形的误差进行了比较。图5a和图5b分别是A点和B点的地震记录误差。从图5可以看出，新推导的交错网格有限差分的正演波形误差更小。因此，新推导的差分格式及差分系数比常规的差分格式及差分系数具有更高的精度。

a.A点；b.B点。图5 常规交错网格差分格式数值解误差与新推导的差分格式数值解误差对比Fig.5 Contrast between conventional staggered grid finite difference format solution error and improved difference format solutions error with analytic solution, respectively

4.2 水平层状模型试算

为了验证新推导出的差分格式对层状介质中的正演效果，建立了图6中的层状地质模型，每层的物性参数如图中所示。网格大小为250×250，空间步长为10 m，2个介质分界面分别在500 m和1 000 m处，震源坐标为(1 250 m，200 m)。在计算时采用新推导的时间4阶、空间8阶精度的差分格式，用主频为25 Hz的Richer子波激发。

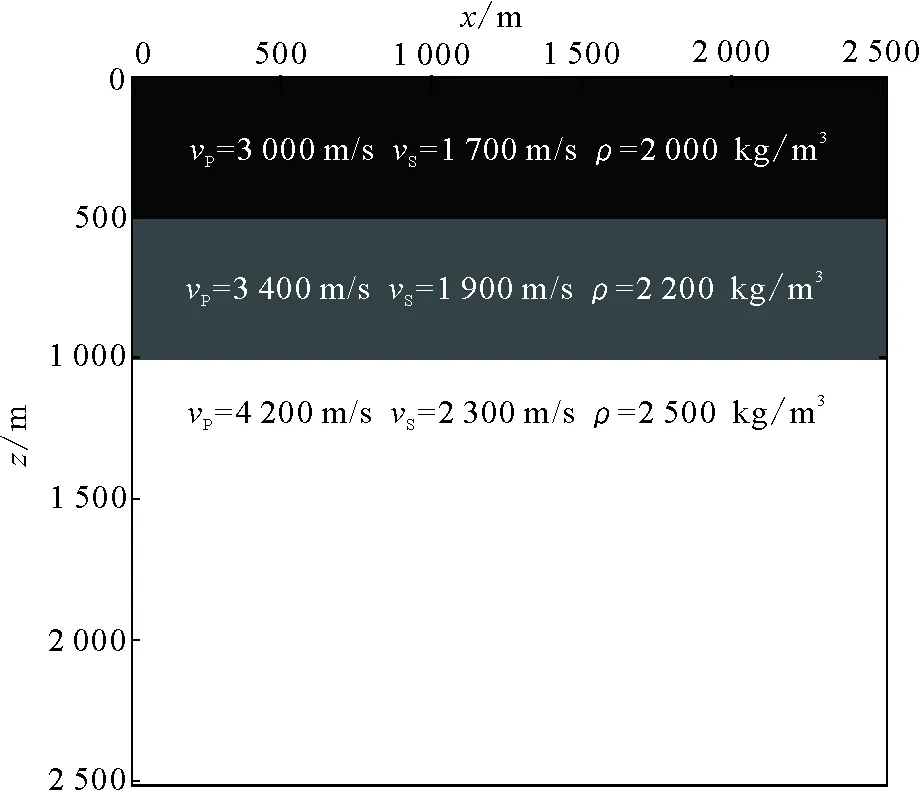
图6 分层介质模型Fig.6 Homogeneous layered model with the layer properties

a．x分量；b．z分量。图7 400 ms时模型波场快照Fig.7 Snapshots of Fig. 6 using the proposed format at time is 400 ms

图7是精度为O(Δt4+Δx8)新推导的差分格式的400 ms波场快照，计算用时为207.9 s。从图7中可以看出:新推导出的高精度交错网格有限差分的差分格式能精确地模拟弹性波在地下层状介质中的传播特性；弹性波在地下500 m处和1 000 m处发生反射和透射，且出现转换横波。在其他计算条件完全一致的情况下，用常规的交错网格有限差分公式模拟图6中的模型计算用时也需要198.5 s，新推导的差分技术计算效率上只相差4.5%，但计算精度提高了，达到了真正的空间2N阶，在本文4.1节已经做过详细的分析对比。

5 结束语

常规高阶交错网格有限差分格式中出现变量对空间二次或三次导数时，采用了低阶的差分格式，并没有达到空间2N阶精度。本文通过Taylor公式展开法，首次推导出了交错网格有限差分算法中的变量任意次导数的任意偶数阶精度的差分格式以及差分系数，完善了传统时间4阶、空间2N阶精度的交错网格有限差分算法，具有重要的理论意义。

[1] 牟永光，裴正林. 三维复杂介质地震数值模拟[M]. 北京：石油工业出版社，2005. Mu Yongguang,Pei Zhenglin.Seismic Numerical Simulation of 3D Complex Medium[M]. Beijing: Petroleum Industry Press, 2005.

[2] 李宾. 横向各向同性介质有限差分法波场模拟方法研究[D]. 北京：中国石油大学，2009. Li Bin. Finite Difference Numerical Modeling of Seismic Wavefields in Tansversely Isotropic Media with a Vertical Axis[D]. Beijing: China University of Petroleum, 2009.

[3] 龙桂华，李小凡，张美根. 错格傅里叶伪谱微分算子在波场模拟中的应用[J]. 地球物理学报，2009，52(1):193-199. Long Guihua, Li Xiaofan, Zhang Meigen. The Application of Staggered-Grid Fourier Pseudo Spectral Differentiation Operator in Wavefield Modeling[J]. Chinese Journal of Geophysics, 2009,52(1):193-199.

[4] 孟庆生，樊玉清，张珂,等.高阶有限差分法管波传播数值模拟[J].吉林大学学报：地球科学版，2011，41(1):292-298. Meng Qingsheng, Fan Yuqing, Zhang Ke, et al. Tube Wave Propagation Numerical Simulation Based on High Order Finite-Difference Method[J]. Journal of Jilin University: Earth Science Edition, 2011, 41(1):292-298.

[5] 周晓华，陈祖斌，曾晓献，等.交错网格有限差分法模拟微动信号[J].吉林大学学报：地球科学版，2012，42(3):852-857. Zhou Xiaohua, Chen Zubin, Zeng Xiaoxian, et al. Simulation of Microtremor Using Straggered-Grid Finite Difference Method[J]. Journal of Jilin University: Earth Science Edition, 2012, 42(3):852-857.

[6] 孙卫涛. 弹性波动方程的有限差分数值方法[M]. 北京：清华大学出版社，2009. Sun Weitao. The Finite Difference Numerical Method of Elastic Wave Equation[M]. Beijing: Tsinghua University Press,2009.

[7] Wang Y, Xu J, Gerard T S. Viscoelastic Wave Simulation in Basins by a Variable-Grid Finite-Difference Method[J]. Bull Seismol Soc Am, 2001, 91(6): 1741-1749.

[8] Narayan J P, Kumar S. A Fourth Order Accurate SH-Wave Staggered Grid Finite-Difference Algorithm with Variable Grid Size and VGR-Stress Imaging Technique[J]. Pure Appl Geophys, 2008, 165:271-294.

[9] Shin Aoi, Hiroyuki Fujiwara. 3D Finite-Difference Method Using Discontinuous Grids[J]. Bull Seismol Soc Am, 1999,89:918-930.

[10] Opršal I, Zahradník J. Elastic Finite-Difference Method for Irregular Grids[J]. Geophysics, 1999,64:240-250.

[11] Madariaga R. Dynamics of an Expanding Circular Fault[J]. Bull Seismol Soc Am, 1976, 66: 639-666.

[12] Virieux J. SH-Wave Propagation in Heterogeneous Media: Velocity-Stress Finite-Difference Method[J]. Geophysics, 1984, 49(11): 1933-1957.

[13] Thomas B, Erik H S. Accuracy of Heterogeneous Staggered-Grid Finite-Difference Modeling of Rayleigh Waves[J]. Geophysics,2006,71(4): 109-115.

[14] Erik H S, Norbert G, Serge A S. Modeling the Propagation of Elastic Waves Using a Modified Finite-Difference Grid[J]. Wave Motion, 2000,31:77-92.

[15] Reeshidev B, Mrinal K S. Finite-Difference Modeling of S-Wave Splitting in Anisotropic Media[J]. Geophysical Prospecting, 2008, 56: 293-312.

[16] Tessmer E. Seismic Finite-Difference Modeling with Spatially Varying Time Steps[J]. Geophysics, 2000,65(4):1290-1293.

[17] Liu Y,Mrinal K S.A Practical Implicit Finite-Diffe-rence Method: Examples from Seismic Modeling[J]. Journal of Geophysics and Engineering, 2009, 6(3): 231-249.

[18] Liu Y, Mrinal K S. Finite-Difference Modeling with Adaptive Variable-Length Spatial Operators[J]. Geophysics, 2011, 76(4): 79-89.

[19] Levander A R. Fourth-Order Finite-Difference P-SV Seismograms[J]. Geophysics, 1988, 53(11):1425-1436.

[20] 董良国，马在田，曹景中，等. 一阶弹性波方程交错网格高阶差分解法[J]. 地球物理学报，2000，43(6)：856-864. Dong Liangguo, Ma Zaitian, Cao Jingzhong, et al. The Stability Study of the Staggered-Grid High-Order Difference Method of One-Order Elastic Equation[J].Chinese Journal of Geophysics, 2000,43(6):856-864.

[21] 董良国，马在田，曹景中. 一阶弹性波方程交错网格高阶差分解法稳定性研究[J]. 地球物理学报，2000，43(3):411-419. Dong Liangguo, Ma Zaitian, Cao Jingzhong. The Staggered-Grid High-Order Difference Method of One-Order Elastic Equation[J].Chinese Journal of Geophysics, 2000,43(3):411-419.

[22] Liu Y, Mrinal K S. Acoustic VTI Modeling with a Time-Space Domain Dispersion-Relation-Based Finite-Difference Scheme[J]. Geophysics,2010,75(3): 11-17.

[23] Hestholm S. Acoustic VTI Modeling Using High-Order Finite Differences[J]. Geophysics, 2009,74(5):67-73.

[24] Finkelstein B, Kastner R. Finite Difference Time Domain Dispersion Reduction Schemes[J]. Journal of Computational Physics, 2007,221: 422-438.

[25] Fei T W, Christopher L L. Hybrid Fourier Finite-Difference 3D Depth Migration for Anisotropic Media[J]. Geophysics, 2008, 73(2): 27-34.

[26] Fornberg B. Generation of Finite Difference Scheme on Arbitrarily Spaced Grids[J]. Mathematics of Computation, 1988, 51: 699-706.

[27] Collino F, Tsogka C. Application of the Perfectly Matched Absorbing Layer Model to the Linear Elasto Dynamic Problem in Anisotropic Hetergeneous Media[J]. Geophysics, 2001,66(1):294-307.

[28] Dablain M A. The Application of High-Order Diffe-rencing to the Scalar Wave Equation[J]. Geophysics,1986, 51:54-66.

《吉林大学学报(地球科学版)》征稿简则

《吉林大学学报(地球科学版)》是以地学为特色的综合性学术期刊，是中文核心期刊、中国科技核心期刊、中国科学引文数据库(CSCD)重要期刊、中国学术期刊评价(2013-2014)(RCCSE)权威期刊。

本刊主要刊登地质与资源、地质工程与环境工程、地球探测与信息技术等学科领域中的最新科研成果。欢迎广大作者踊跃投稿。

投稿注意事项如下：

1 来稿必须是未正式发表的、具有创新性成果的科技论文；必须是受到省部级及以上科研基金资助的立项课题的主要研究成果。

2 来稿要求论点明确、数据可靠、逻辑严密、文字精炼。每篇论文必须包含题目、作者姓名、作者单位(以上需中英文对照)及邮政编码、中英文摘要和关键词、中国图书馆分类号、正文、参考文献及第一作者和通信作者简介，并且在文稿首页地脚处注明论文属何项目(基金)资助及项目编号。作者简介格式为：姓名(出生年-)、性别、民族(汉族可省略)、职称、学位、研究方向、电话(可省略)、电子信箱。

3 论文摘要须写成报道性文摘，包括目的、方法、结果、结论4部分(200～500字)，摘要应具有独立性与自明性。摘要应由正文中重要语句组成。

4 文稿篇幅(含图表)一般不超过1万字，文中量和单位必须使用法定的量和计量单位，外文字母必须分清大小写、正斜体、黑白体、上下角标字符的位置应区别明显。

5 文中图表应有自明性，图表应附相应的中英文名。附图力求简明清晰，经纬度、比例尺、图例等内容齐全。图中文字(汉字用宋体，数字和字母用Times New Roman体；字号相当于Word文档中的小5至6号字大小)、符号、纵横坐标必须写清，并与正文一致；坐标标值线应放在坐标轴内侧，标目中的量和单位间用斜线(如：t/s，变量字母t用斜体)。凡涉及国界线的图件必须绘制在地图出版社公开出版的最新地理底图上。图版长×宽不超过23cm×16cm，照片要求清晰，层次分明。文稿中须留出插图位置。

6 参考文献只选最主要的列入，并要注意引用近两年国内外的文献。文后参考文献表采用顺序编码制，按文中出现的先后顺序编号。中文文献要附上相应的英译文献，英译时责任者的姓名首字母大写，双名连拼。英文文献责任者姓名姓前名后：姓全拼，首字母大写；名缩写，不加缩写点。英译文献及英文文献的责任者不超过3人时全部写出，超过时只写前3名，后加“等”或“et al．”；题名、刊名实词首字母均大写。

不同文献的著录格式如下：

(1) 专著的著录格式：[序号]主要责任者(作者、编者等)．题名(书名)[M]．版本(第一版不标注)．出版地：出版者，出版年．

(2) 论文集中析出文献的著录格式：[序号]作者．题名[C]//编者．论文集名．版本(第一版不标注)．会议地址：承办单位(或出版地：出版者)，出版年：起止页码．

(3) 连续出版物文献的著录格式：[序号]作者．题名[J]．期刊名，年，卷(期)：起止页码．

(4) 专利的著录格式：[序号]专利申请者．专利题名[P]．国别，专利文献种类，专利号．出版日期．

(5) 学位论文的著录格式：[序号]作者．题名[D]．保存地点：保存单位，年份．

(6) 技术标准的著录格式：[序号]标准代号．标准顺序-发布年．标准名称[S]．出版地：出版者，出版年．

(7) 报告的著录格式：[序号]作者. 题名[R]. 保存地：保存单位，保存年.

(8) 电子文献的著录格式：[序号]主要责任者(作者)．电子文献题名[电子文献及载体类型标识]．发表或更新日期/引用日期(任选)．电子文献的出处或可获得地址.

7 请勿一稿多投。投稿3个月后仍未接到反馈信息者，请与编辑部联系。

8 本刊已加入《中国学术期刊(光盘版)》及其他数据库，其作者文章著作权使用费与本刊稿酬一次性给付。如作者不同意文章被收录，请在来稿时向本刊声明，本刊将做适当处理。

请作者提供正文的电子文档(方正、Word均可)，并提供矢量图格式文件，图件尽量使用CorelDraw绘制。

通信地址：吉林省长春市西民主大街938号《吉林大学学报(地球科学版)》编辑部。邮编130026。

电子信箱: xuebao1956@jlu.edu.cn 本刊网址：http://xuebao.jlu.edu.cn/dxb

电 话：0431-88502374 发行代号：12-22(国内)；BM5074(国外)

Staggered Grid Finite Difference Scheme and Coefficients Deduction of Any Number of Derivatives

Yang Qingjie, Liu Cai, Geng Meixia, Feng Xuan, Guo Zhiqi, Liu Yang

CollegeofGeoExplorationScienceandTechnology,JilinUniversity,Changchun130026,China

Staggered grid finite difference algorithm is effective, accurate and practical, so it has wide application prospect and practical significance.So far, the common high-order scheme of staggered grid finite difference algorithm is 4-order temporal and 2N-order spatial accuracy.However, the FD scheme isn’t 2N-order accuracy actually when computing second or third spatial derivative.The authors deduce the FD scheme with 2N-order accuracy and corresponding coefficients of any number of derivatives of functions which have any number of derivatives forthefirsttime.So we can consummate conventional high-order staggered grid finite difference algorithm.We make a simulation of seismic response with conventional FD scheme and the new FD scheme respectively，and compared with analytic solution respectively. As a result, the new FD scheme is more stabilized and more accurate.

staggered grid; finite difference scheme; finite difference coefficients; high-order

10.13278/j.cnki.jjuese.201401307.

2013-07-01

国家自然科学基金项目(40974054，41174080)；国家“973”计划项目(2009CB219301)；油页岩勘探开发利用产学研用合作创新研究项目(OSP-02，OSR-02)

杨庆节(1987-)，男，博士研究生，主要从事多波多分量地震勘探研究，E-mail:qjyang58@gmail.com

刘财(1963-)，男，教授，博士生导师，主要从事地震波场正反演理论、综合地球物理等研究，E-mail:liucai@jlu.edu.cn。

10.13278/j.cnki.jjuese.201401307

P631.4

A

杨庆节，刘财，耿美霞，等.交错网格任意阶导数有限差分格式及差分系数推导.吉林大学学报:地球科学版,2014,44(1):375-385.

Yang Qingjie, Liu Cai, Geng Meixia,et al.Staggered Grid Finite Difference Scheme and Coefficients Deduction of Any Number of Derivatives.Journal of Jilin University:Earth Science Edition,2014,44(1):375-385.doi:10.13278/j.cnki.jjuese.201401307.